لماذا يعتبر كبار علماء الفيزياء القياسات الكمومية الضعيفة علمًا زائفًا؟

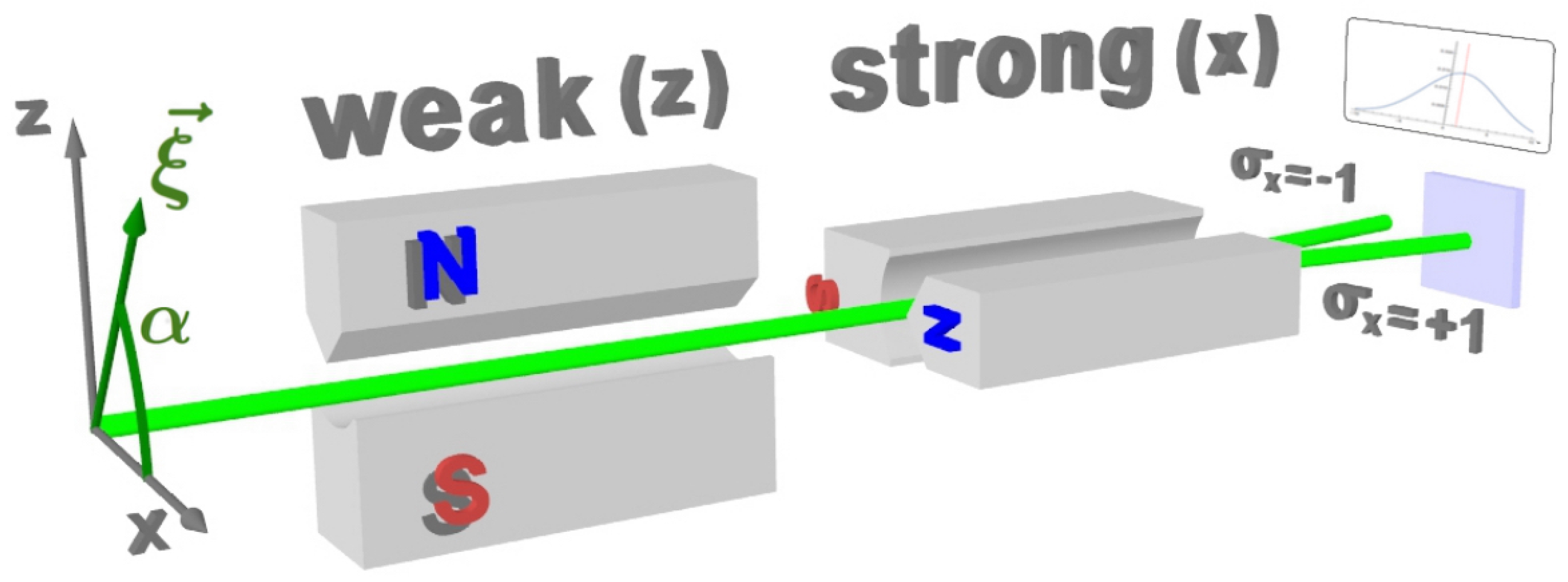
تعد القياسات الضعيفة (القياسات الضعيفة ، والقياسات الخالية من التفاعل ، والقياسات المعكوسة ، والقياسات غير التلامسية ) نموذجًا معروفًا إلى حد ما في دوائر ضيقة ، حتى تم ذكرها في Habré . تم طرح الفكرة والترويج لها منذ التسعينيات من قبل المدرسة الإسرائيلية للفيزيائيين (ياكير آرونوف ، ليف ويدمان والعديد من الشخصيات الأقل شهرة) ، ويتلخص في حقيقة أن افتراضات ميكانيكا الكم حول القياس يمكن التحايل عليها.

هذا هو الافتراض المؤسف:

عند القياس ، ينهار متجه الحالة (دالة الموجة) في أحد متجهات التهيئة (وظائف) المشغل للكمية المقاسة.

يعتقد الفيزيائيون الإسرائيليون ضمناً (وبشكل خاطئ) أن الانهيار يحدث عندما يتفاعل جهاز القياس مع النظام المقاس. لذلك ، يكون منطقهم كما يلي: دعنا نفكر في كيفية قياس النظام دون تفاعل مادي مع أي شيء مع هذا النظام. ثم سنثبت أن القياس قد تم ، لكن الانهيار لم يحدث. وقادوا تجربة التفكير التالية ، المعروفة الآن على نطاق واسع بفضل روجر بينروز.

قنابل إليتزور ويدمان الكمومية

فليكن هناك قنابل حساسة لدرجة أنها تنفجر عندما تضرب جسيمًا أوليًا واحدًا ، مثل الفوتون. من المعروف أن بعض القنابل مكسورة ، لكن من غير المعروف أي منها. المهمة هي فرز القنابل غير العاملة من العمال دون تفجيرها.

في ظل الظروف المذكورة ، تبدو المهمة غير قابلة للحل. للتحقق من أداء قنبلة ، تحتاج إلى تفكيكها أو القيام بشيء آخر معها. في أي حال ، سوف تضطر إلى لمسها ، ولكن وفقًا لقواعد اللعبة ، سيؤدي ذلك إلى حدوث انفجار. في الواقع ، في إطار الفيزياء الكلاسيكية ، من المستحيل اختبار مثل هذه القنبلة للتشغيل دون تفجيرها. ومع ذلك ، في عالمنا الكم ، أي شيء تقريبا ممكن.


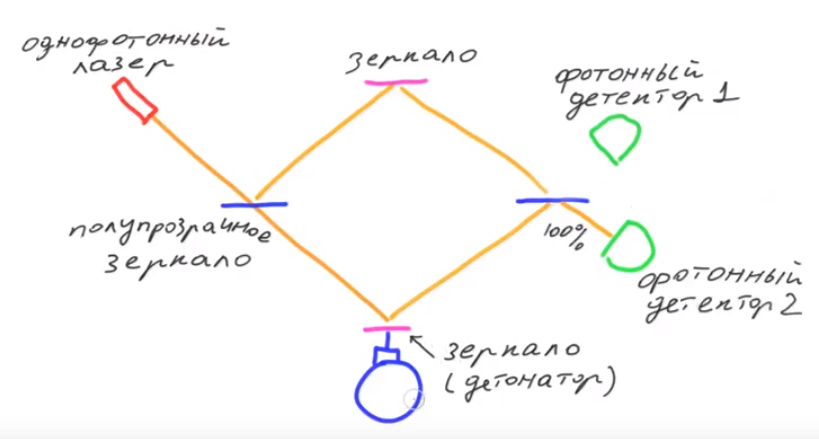
ضع القنبلة على أحد أذرع مقياس التداخل ماخ زيندر. دع المرآة تكون جزءًا من القنبلة. إذا لم تعمل القنبلة ، فسيعمل مقياس التداخل. كلتا ذراعي مقياس التداخل متطابقتان ، والمعلومات المفقودة عن أي من الأسلحة التي مر عليها الفوتون. سيتم ملاحظة التداخل وستسقط جميع الفوتونات في كاشف أقل.

إذا حصلت القنبلة على قنبلة عاملة ، فسيكون التداخل غير فعال. الكتفين الآن ليست متطابقة. الفوتون الذي يمر على طول الكتف السفلي سيؤدي إلى انفجار قنبلة. لن يكون هناك أي تدخل بعد الآن ، حيث توجد معلومات حول أي من الأكتاف التي مر بها الفوتون (انفجرت القنبلة أم لا).

يمكن أن يرتد الفوتون من المرآة الشفافة الأولى ، ويمر فوق الكتف العلوي ، ويرتد من المرآة الشفافة الثانية ، ويسقط في الكاشف العلوي. لكن لاحظ أنه في حالة وجود قنبلة غير عاملة ، لا يمكن أن يكون في جهاز الكشف العلوي - وهذا يعني أن القنبلة تعمل. لكنها لم تنفجر بينما سار الفوتون على طول الكتف العلوي. يشير تثبيت الفوتون بواسطة جهاز الكشف العلوي إلى أن القنبلة جاهزة للعمل وفي نفس الوقت تظل سليمة.


مناقشة أكثر تفصيلا لتجربة Elitzur- ويدمان هنا .
هل دحض الفيزيائيون اليهود القياس الذي افترضته هذه التجربة؟ بالطبع لا. ما هو الخطأ في منطقهم؟ المشكلة هي أنهم لا يفهمون أن القياس هو استلام المراقب للمعلومات ، وليس تفاعل النظام مع جهاز القياس. عندما يتلقى المراقب بيانات جديدة ينهار متجه الحالة. حقيقة أن المعلومات حول قابلية تشغيل القنبلة لم يتم عن طريق التفاعل المادي المباشر مع جهاز القياس لا تغير أي شيء.

هل سيفاجأ الآباء المؤسسون للميكانيكا الكمومية بهذه التجربة العقلية قبل نشرها؟ بالطبع لا! لا عجب أنهم أدخلوا مفهوم "المراقب" في ميكانيكا الكم. إذا كان جهاز القياس مراقبًا ، فسيكون هذا المصطلح المادي الإضافي غير ضروري.

من أو ما هو إذن المراقب؟ الشخص الذي يتلقى بيانات جديدة هو مراقب. هو بالنسبة له أن ميكانيكا الكم يعطي تنبؤات احتمالية لنتائج القياسات المستقبلية على أساس البيانات المتاحة حاليا له.

التشابك الكمي وانهيار ناقلات الحالة

حقيقة أن الانهيار ليس عملية فيزيائية ، ولكن فقط تحديث معرفة المراقب للنظام عندما تلقى بيانات جديدة ، كانت معروفة بالطبع للآباء المؤسسين. دعونا نأخذ التجربة الكلاسيكية للتشابك الكمومي ، التي ناقشها نيلز بور نفسه في نزاع مع آينشتاين.


يتحلل pi-meson إلى إلكترون وبوزيترون ، ينفصلان عند أطراف مختلفة من المجرة. ظهورهم مشوشة. عند قياس كل من الدوران فيما يتعلق بالاتجاه نفسه للمحور ، سيكونان دائمًا متعاكسين لإعطاء إجمالي صفري.

من المستحيل التنبؤ بدقة بما سيكون عليه الدوران بدون معلومات حول نتيجة قياس الدوران للجسيم الثاني. لنفترض أن أليس أراد قياس تدور الإلكترون بالنسبة للمحور z واتضح أنه +1 / 2. ينهار متجه الحالة في ناقل متجه.

ماذا حدث لمتجه الدولة للمراقب الثاني ، بوب ، بعد البوزيترون؟ لا تهتم. بالنسبة له ، لم يتغير شيء. يعرف أليس أنه إذا أراد بوب قياس دوران البوزيترون نسبة إلى المحور z ، فسوف يحصل على -1/2. لكن بوب لا يعرف ذلك. متجه الحالة لم ينهار بعد. متى سيحدث الانهيار لبوب؟

1. سيقوم بقياس دوران البوزيترون نسبة إلى المحور z ، والكشف عن -1/2 ، وسيقوم ناقله بالانهيار في ناقل "الدوران".

2. سترسله Alice معلومات حول نتيجة قياسها ، وعند الاستلام ، سينقلب المتجه أيضًا إلى "تدور" نسبة إلى المحور z.

الخيار الثاني هو ما بدأ العلماء الإسرائيليون في تسميته "قياسات خالية من التفاعل" (قياسات عدم الاتصال). كما ترون ، لم يخترعوا شيئًا جديدًا ولكن مصطلحًا إضافيًا لا لزوم له. ينهار ناقل الحالة في أي حال ، وبالتحديد في لحظة الحصول على معلومات جديدة حول النظام. هذا الانهيار ، بحكم تعريفه ، هو بعد.

لاحظ أن بوب قد يختار بعض المحور الآخر ، وليس بالضرورة z. دعنا نقول أن محورها ينحرف بعدة درجات عن محور أليس.


بدون معلومات من Alice حول نتيجة قياسها ، تكون جميع قياسات Bob عشوائية تمامًا (هذه خاصية لحالة الفردي : فيما يتعلق بأي اتجاه للمحور ، فإن الدوران سيكون "صاعدًا" باحتمال 50٪ ونزولًا باحتمال 50٪).

ومع ذلك ، إذا كان قبل قياسه يتلقى معلومات من أليس ، ثم ينهار متجه الدولة. يتم إعادة توزيع الاحتمالات. دعنا نقول 90 ٪ أن تدور له سيكون "لأسفل" و 10 ٪ "أعلى" إذا كان أليس "أعلى". وإذا تم رفض دوران "Alice" ، فعندما يتم استلام هذه المعلومات (الأخرى) ، فإن الموجه ينهار إلى ناقل آخر ، مما يعطي 10٪ "لأسفل" و 90٪ "أعلى".

تسمح ميكانيكا الكم لأحد الحصول على صيغة دقيقة لمثل هذه الارتباطات الاحتمالية ، والتي يستنتج منها أيضًا أنه من المستحيل تحمل اتجاه الدوران كما هو محدد حتى يتم الحصول على معلومات حول نتيجة القياس. لا يتغير تدور البوزيترون في الطرف الآخر من الكون فورًا عند قياس تدور الإلكترون المتشابك معه ، كما يدعى كثيرًا. ونعم ، نقل المعلومات الفائق أمر مستحيل لأن أليس تحصل على نتائج عشوائية عند قياس دوران الإلكترون.

بشكل عام ، على الرغم من جهود الفيزيائيين الإسرائيليين ، لن ينهار الانهيار. عند القياس (الحصول على بيانات جديدة) ، ينهار المتجه ، مما يعكس ببساطة تحديث المعرفة الشخصية للمراقب بالنظام ، والتي يتم تشفيرها في هذا المتجه (دالة الموجة).

واجبات أتباع التفسير العالمي: احصل على نفس النتائج من مفهوم إيفريت. قل لي بالضبط متى ينقسم العالم في هذه الحالة وعدد الفروع.

"التناقض" لعش الحمام

لكن الفيزيائيين الإسرائيليين لا يستسلمون ، وهنا مقال آخر يستخدم فيه المؤلفون (آرونوف في al.) النهج الموضح " القياس لا يؤدي دائمًا إلى الانهيار " لاشتقاق مثل هذا التصريح السخيف الذي:

يمكن حشر ثلاثة حمامات في فتحتين للحمام ، ولن يكون هناك حمامان في أي من الثقوب.

هذا ما يحدث إذا أهملنا افتراضات ميكانيكا الكم! وقد تبين عدم توافق هذا البيان للفيزيائيين اليهود مع ميكانيكا الكم عدة مرات. أوصي بمقال للأستاذ السابق في جامعة هارفارد ، لوبوس موتل ، بعنوان " ثلاثة ثقوب حمامة في أدمغة ستة علماء فيزياء ".