يتم تزويد الويب العالمية يوميًا بمقالات عن خوارزميات التعلم الآلي الأكثر شيوعًا والأكثر استخدامًا لحل المشكلات المختلفة. علاوة على ذلك ، فإن أساس هذه المقالات ، الذي تغير قليلاً في شكله في مكان أو آخر ، يتجول من باحث بيانات إلى آخر. علاوة على ذلك ، يتم توحيد كل هذه الأعمال من خلال افتراض مقبول لا يقبل الجدل بشكل عام: يعتمد تطبيق خوارزمية واحدة أو أخرى للتعلم الآلي على حجم وطبيعة البيانات المتاحة والمهمة قيد البحث.
بالإضافة إلى ذلك ، لا سيما الباحثين
المعتمدين على البيانات ، الذين يشاركون خبراتهم ، يشددون على:
"يجب أن يعتمد اختيار طريقة التقييم جزئيًا على بياناتك وعلى ما يجب أن يكون عليه النموذج في رأيك" (علم البيانات: معلومات داخلية للمبتدئين). بما في ذلك لغة البحث والتطوير (R) ، بقلم كاثي أونيل ، وراشيل شات) .
بمعنى آخر ، لا ينبغي أن يتمتع الباحث الإحصائي / باحث البيانات بخبرة في مجال الموضوع فحسب ، بل يتمتع أيضًا بمجموعة واسعة من المعرفة المتنوعة:
"باحث البيانات هو الذي لديه معرفة في المجالات التالية: الرياضيات والإحصاء وهندسة الكمبيوتر والتعلم الآلي والتصور ، يعني تبادل البيانات ... " (من نفس الكتاب). فقط تحميل المعرفة بدقة من المناطق المذكورة أعلاه إلى الرأس يمكنه التعامل مع التعلم الآلي وإيجاد حلول للمشاكل المشار إليها.
بالنسبة لي ، هذه البداية مناسبة تمامًا لكتاب منتظم واحد ونصف كيلوغرام عن علم البيانات ، أو مقالة رعب علمية مع صيغ "لا قيمة لها" لاحقة من طابقين ، والرموز والنصائح التي لها تأثير كئيب وخطير على المبتدئين في مجال التعلم الآلي ، وفقط بالصدفة المهتمين في هذا الاتجاه القراء عديمي الخبرة ، وليس مثقلة "المعرفة اللازمة". بالإضافة إلى ذلك ، فإن الجولة رقم 10 من نفس المقالات حول خوارزميات التعلم الآلي الأكثر شيوعًا (
على سبيل المثال ) تعزز فقط التأثير المفروض.
في habr ، ميزوا أنفسهم أيضًا :
"الإجابة على السؤال:" ما نوع خوارزمية التعلم الآلي التي يجب استخدامها؟ "يبدو دائمًا هكذا:" وفقًا للظروف ". يعتمد اختيار الخوارزمية على حجم وجودة وطبيعة البيانات. ذلك يعتمد على كيفية إدارة النتيجة. يعتمد ذلك على كيفية إنشاء إرشادات الكمبيوتر التي ينفذها من الخوارزمية ، وكذلك على مقدار الوقت المتاح لديك. حتى أكثر محللي البيانات خبرة لن يخبركوا بالخوارزمية الأفضل حتى يجربوها ".مما لا شك فيه ، كل هذه المعرفة ، وكذلك المثابرة والاهتمام ضرورية ومفيدة في تحقيق نتائج جيدة ليس فقط على طريق فهم التعلم الآلي ، ولكن أيضًا في العديد من المجالات الأخرى. بالإضافة إلى ذلك ، سوف يسهلون فهم أن خوارزميات التعلم الآلي (المشار إليها فيما يلي باسم الخوارزميات) بعيدة عن العشرات ؛ ولكن هذا فقط في وقت لاحق ، مع دراسة مستقلة.
هدفي هو تقديم القارئ إلى الخوارزميات الأكثر استخدامًا من وجهة نظر عملية ويمكن الوصول إليها. (حقيقة أنني لست مبرمجًا ، علاوة على ذلك ، لست عالمة رياضيات (مقدسة!) يجب أن تؤكد الاهتمام بالسرد. التعليم الهندسي بالإضافة إلى الخبرة في "نمو الموضوع" لمدة 10 سنوات (مجرد نوع من الرقم السحري ) - كما يقولون ، وكل ما عندي من أمتعتي ، كل أمتعتي التي توجهت بها مباشرةً للتعلم الآلي. بفضل تجربتي في صناعة النفط ، تم العثور على أفكار لاستخدام الشبكات العصبية الاصطناعية وخوارزميات التعلم الآلي على الفور (قراءة - كانت هناك ضرورة مجموعات البيانات.) كل ما تبقى كان للتعامل معها القرمزي - تعلم كيف تقوم بتحريف البيانات من أجل تقديمها بشكل صحيح إلى مدخلات "البرنامج" والتي في الواقع خوارزمية تختارها ، ثم في حلقة مفرغة. ألاحظ أن طريقي كان شائكًا وممتعًا - "رصاصة صفير النفقات العامة" (من م / f "The Adventures of Funtik") - ولكن ما زلت تمكنت من تدوين الملاحظات ، وإذا تمت الإشارة إلى الاهتمام ، فسننشر في المستقبل رسائل أخرى في المستقبل.)
لذلك ، أقترح الاقتراب من "المعالجة الآلية" من ناحية أخرى: لماذا لا تغذي مجموعة البيانات الموجودة لديك (في الأمثلة التي ستقوم بتحميل مجموعات البيانات التي يمكن تدريبها بسهولة) على العديد من الخوارزميات في وقت واحد ، ومن خلال النتائج ، تقرر أي منها ستولي اهتمامًا أكبر دراسة متأنية لاحقة واختيار المعلمات المثلى التي تعزز النتيجة. علاوة على ذلك ، فإن القيمة الرئيسية للطريقة التي تمت مناقشتها أعلاه هي أن نتائجها سوف تجيب على السؤال عن مدى أهمية مجموعة البيانات الخاصة بك:
"ابدأ بحل المشكلة وتأكد من أن لديك شيئًا لتحسينه" (أيضًا من البعض ثم ذهب إحصاءات إصرار ، "احترام" له ، نصيحة جيدة!).
كيف يتم صنعه؟
من المعروف أن الجزء الأكبر من المشكلات التي يتم حلها بمساعدة الخوارزميات يتعلق بمشكلات التصنيف (التصنيف) وتحليل الانحدار (التحليل التنبئي). يُقصد
بالتصنيف تمايزًا ثابتًا بين وحدات الملاحظة (مثيلات) مجموعة البيانات إلى فئة معينة (فئة) استنادًا إلى نتائج التدريب.
تحليل الانحدار هو مجموعة من الأساليب والعمليات الإحصائية لتقييم العلاقة بين المتغيرات [
الإحصائيات: كتاب نص / إد. أ. MR إفيموفا. - M: INFRA-M ، 2002 ]. الغرض من تحليل الانحدار هو تقييم قيمة متغير الإخراج المستمر من قيم متغيرات الإدخال [
link ].
نتجاهل حقيقة أن تحليل الانحدار لديه تحت تصرفه طريقتين مختلفتين - النمذجة التنبؤية والتنبؤ. نلاحظ فقط أنه في حالة وجود سلسلة زمنية (بيانات السلاسل الزمنية) ، ثم باستخدام نموذج الانحدار استنادًا إلى اتجاه صريح ، رهنا بثبات (ثبات) ، يمكن إجراء التنبؤ. إذا تغيرت شروط تكوين مستويات السلاسل الزمنية ، أي أنه لم تتم ملاحظة العملية غير الثابتة ، فإن الأمر يتوقف على النمذجة التنبؤية. تهدف بشكل خاص إلى إتقان ML الكامل ، أقترح قراءة هذه المقالة باللغة الإنجليزية:
link . إذا نشأ نقاش حول هذا الموضوع ، سأكون سعيدًا بالمشاركة فيه.
نظرًا لعدم استخدام السلاسل الزمنية في الأمثلة الواردة في هذه المقالة ، يشير مصطلح
التنبؤ إلى
التحليل التنبئي .
لحل مشاكل التصنيف والتنبؤ ، تعد مجموعة كاملة من الخوارزميات مناسبة ، والتي سننظر فيها لاحقًا. للراحة ، سيتم تقسيم النص التالي إلى جزأين: في الجزء الأول ، نعتبر خوارزميات التصنيف الأكثر شيوعًا ، والثاني الذي نخصصه لخوارزميات تحليل الانحدار. لكل جزء ، سيتم تقديم مجموعة بيانات "لعبة" تم تحميلها من
مكتبة تعلم scikit (v0.21.3):
مجموعة بيانات الأرقام (التصنيف) ومجموعة
بيانات أسعار منزل بوسطن (الانحدار) ، بالإضافة إلى روابط لكل خوارزمية مكتبة تعلم scikit للفحص الذاتي ، وربما للدراسة.
يتم تنفيذ جميع أمثلة التعليمات البرمجية في وحدة التحكم
IDE Spyder 3.3.3 على Python 3.7.3.
مشكلة التصنيف
أولاً ، نستورد الوحدات والوظائف اللازمة التي سنستخدمها لحل مشكلة تصنيف البيانات:
قم بتنزيل مجموعة بيانات "الأرقام" مباشرةً من
وحدة "sklearn.datasets" :
توفر IDE Spyder أداة ملائمة "مدير متغير" ، وهي مفيدة في جميع الأوقات لدراسة التعلم الآلي (على الأقل بالنسبة لي) ، مثل
"الحيل" الأخرى :
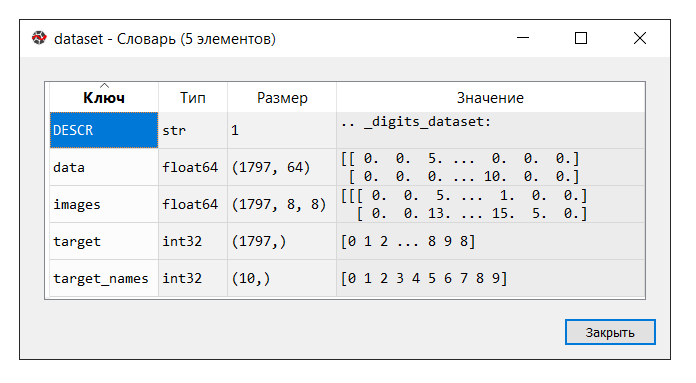
قم بتشغيل الكود. في وحدة التحكم "manager manager" ، انقر فوق متغير
مجموعة البيانات . يتم عرض القاموس التالي:
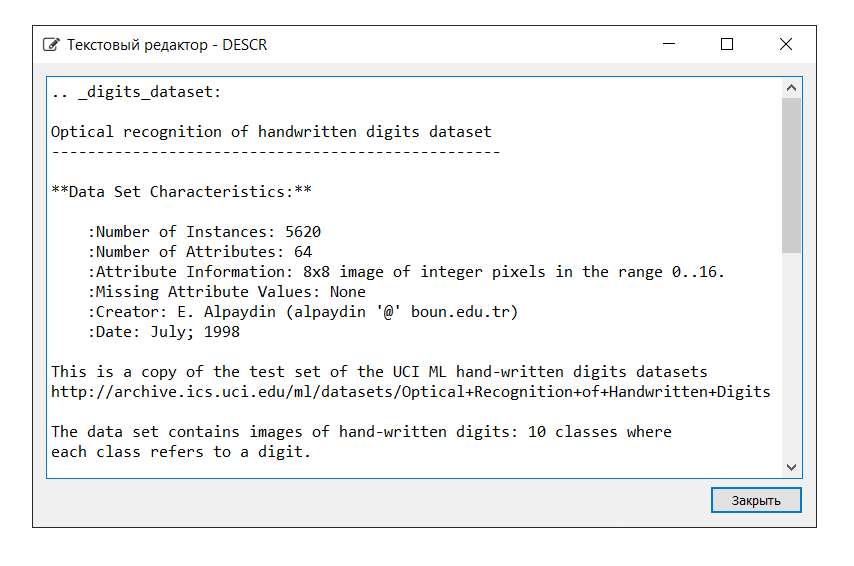
وصف مجموعة البيانات كما يلي:
في هذا المثال ، لا نحتاج إلى مفتاح "الصور" ، لذلك نقوم بتعيين المتغير "بيانات" إلى المتغير
X ، وهو عبارة عن صفيف NumPy متعدد الأبعاد مع مجموعة من السمات ، بحجم 1797 صفًا في 64 عمودًا ، والمتغير
Y إلى "الهدف" ، صفيف NumPy متعدد الأبعاد مع علامة لكل الخط.
بعد ذلك ، نقسم البيانات إلى أجزاء التدريب والاختبار ، ونقوم بتكوين المعلمات لتقييم الخوارزميات (يتم استخدام التحقق المتبادل [
واحد ،
اثنان ]) ، مع تحديد "الدقة" المترية في المعلمة "تسجيل النتائج" [
الارتباط ]. الدقة هي نسبة الكائنات المصنفة بشكل صحيح بالنسبة إلى إجمالي عدد الكائنات. كلما كانت النتيجة أقرب إلى 1 ، كان ذلك أفضل [
link ]. علاوة على ذلك ، في أحد الكتب تبين أن النتائج من 0.95 (أو 95 ٪) وأعلى تعتبر ممتازة.
دع المتغيرات
X_train و
Y_train تستخدمان لأغراض التدريب ،
X_test و
Y_test لتطوير قيم التنبؤ. في هذه الحالة ،
لا يشارك المتغير
Y_test في حساب التوقع: باستخدام طريقة الدرجات ، والتي هي نفسها لكل من الخوارزميات المعروضة أدناه ، سنقوم بحساب الإجابات الصحيحة باستخدام مقياس الدقة. سيتيح لنا ذلك الحكم على كيفية تعامل الخوارزمية مع المهمة. أنا لا أجادل ، من جانبنا ، إنه حقير بشريًا ألا يدفع السيارة بالإجابات الصحيحة ، ولكن كيف للتحقق من أدائها؟
فيما يلي قائمة بالخوارزميات التي نقوم بتغذية مجموعة البيانات بها. استنادًا إلى نتائج العمليات الحسابية ، سوف نستنتج أي الخوارزمية (أي من الخوارزميات) تُظهر أعلى كفاءة. قد يطلق على هذه الطريقة
"اختبار الغارة لخوارزميات التعلم الآلي" (المشار إليها فيما يلي - اختبار الغارة).
للراحة ، سيتم اختصار المعلومات بجوار كل خوارزمية. تجدر الإشارة إلى أنه يتم قبول إعدادات كل خوارزمية افتراضيًا (افتراضيًا) ، باستثناء بعض النقاط ، من أجل توفير شروط متساوية.
الخوارزميات الخطية:
- الانحدار اللوجستي * /
الانحدار اللوجستي ('LR')
* كلمة "الانحدار" يمكن أن تكون مربكة. لكن لا تنسَ أن "الانحدار اللوجستي" هو خوارزمية تصنيف-
تحليل التمييز الخطي (LDA)
الخوارزميات غير الخطية:
- طريقة أقرب جيران (تصنيف) / تصنيف
K- الجيران ("KNN")
-
مصنف شجرة القرار (CART)
-
تصنيف ساذج بايز ('NB')
- طريقة
تصنيف ناقلات الدعم الخطي (التصنيف) /
تصنيف ناقلات الدعم الخطي ('LSVC')
- طريقة
متجه الدعم (التصنيف) /
تصنيف متجه الدعم C ('SVC')
خوارزمية الشبكة العصبية الاصطناعية:
-
متعدد الطبقات Perceptron /
متعدد الطبقات Perceptrons ('MLP')
مجموعة الخوارزميات:
- التعبئة (التصنيف) /
مصنف الحقائب ('BG') (التعبئة = تجميع التمهيد)
-
تصنيف الغابات العشوائي (RF)
-
مصنف الأشجار الإضافية ("ET")
- AdaBoost (تصنيف) /
AdaBoost Classifier ('AB') (AdaBoost = Boosting Boosting)
- تعزيز التدرج (التصنيف) / مصنف تدعيم
التدرج ("GB")
وبالتالي ، فإن قائمة "النماذج" تحتوي على النماذج التالية:
models = [] models.append(('LR', LogisticRegression())) models.append(('LDA', LinearDiscriminantAnalysis())) models.append(('KNN', KNeighborsClassifier())) models.append(('CART', DecisionTreeClassifier())) models.append(('NB', GaussianNB())) models.append(('LSVC', LinearSVC())) models.append(('SVC', SVC())) models.append(('MLP', MLPClassifier())) models.append(('BG', BaggingClassifier(n_estimators=n_estimators))) models.append(('RF', RandomForestClassifier(n_estimators=n_estimators))) models.append(('ET', ExtraTreesClassifier(n_estimators=n_estimators))) models.append(('AB', AdaBoostClassifier(n_estimators=n_estimators, algorithm='SAMME'))) models.append(('GB', GradientBoostingClassifier(n_estimators=n_estimators)))
كما ذكرنا سابقًا ، يتم تقييم فعالية كل خوارزمية باستخدام التحقق المتبادل. نتيجة لذلك ، يتم عرض رسالة (msg - اختصار للرسالة) تحتوي على المعلومات التالية: اسم النموذج في شكل اختصار ، ومتوسط درجة التحقق من صحة 10 أضعاف على بيانات التدريب ("الدقة" المترية) ، ويظهر الانحراف المعياري بين قوسين ، وكذلك قيمة مقياس "الدقة" على بيانات الاختبار.
بعد تشغيل الكود ، نحصل على النتائج التالية:
LR: train = 0.957 (0.014) / test = 0.948 LDA: train = 0.951 (0.014) / test = 0.946 KNN: train = 0.985 (0.013) / test = 0.981 CART: train = 0.843 (0.033) / test = 0.830 NB: train = 0.819 (0.048) / test = 0.806 LSVC: train = 0.942 (0.017) / test = 0.928 SVC: train = 0.343 (0.079) / test = 0.342 MLP: train = 0.972 (0.012) / test = 0.961 BG: train = 0.952 (0.021) / test = 0.941 RF: train = 0.968 (0.017) / test = 0.965 ET: train = 0.980 (0.010) / test = 0.975 AB: train = 0.827 (0.049) / test = 0.823 GB: train = 0.964 (0.013) / test = 0.968
مخطط Span (
"مربع مع شارب" ) (رسم تخطيطي للمربع وشعيرات أو مخطط مؤامرة):
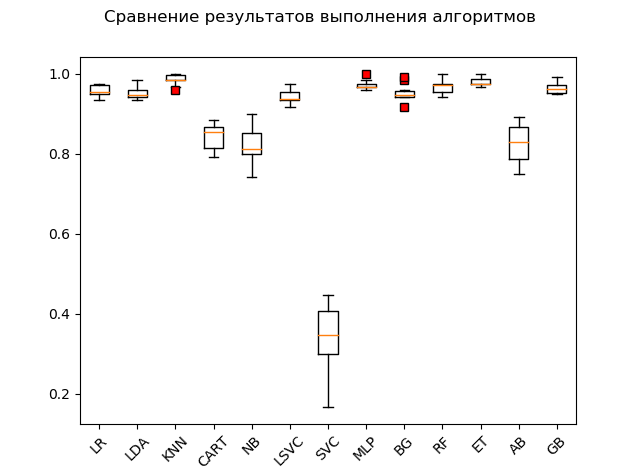
نتيجة لاختبار بدء التشغيل على البيانات الأولية ، يمكن ملاحظة أن الأكثر فعالية في بيانات الاختبار كانت الخوارزميات "KNN" (أقرب جيران) ، "ET" (الأشجار الإضافية) ، "GB" (التدرج "التعزيز") ، 'RF' (غابة عشوائية) و 'MLP' (الإدراك المتعدد الطبقات):
KNN: train = 0.985 (0.013) / test = 0.981 ET: train = 0.980 (0.010) / test = 0.975 GB: train = 0.964 (0.013) / test = 0.968 RF: train = 0.968 (0.017) / test = 0.965 MLP: train = 0.972 (0.012) / test = 0.961 LR: train = 0.957 (0.014) / test = 0.948 LDA: train = 0.951 (0.014) / test = 0.946 BG: train = 0.952 (0.021) / test = 0.941 LSVC: train = 0.942 (0.017) / test = 0.928 CART: train = 0.843 (0.033) / test = 0.830 AB: train = 0.827 (0.049) / test = 0.823 NB: train = 0.819 (0.048) / test = 0.806 SVC: train = 0.343 (0.079) / test = 0.342
ومع ذلك ، فإن العديد من الخوارزميات منتقاة للغاية بشأن البيانات التي يتم تقديمها. لذلك ، فإن إحدى الخطوات الضرورية هي ما يسمى بإعداد البيانات الأولية (المعالجة المسبقة للبيانات [
رابط ])
ومع ذلك ، يحدث أن تظهر الخوارزمية أفضل النتائج دون معالجة أولية. ومن هنا التوصية التالية: تضمين اختبار بدء التشغيل العديد من التحويلات لمجموعة البيانات الأصلية ، وبعد إجراء العمليات الحسابية ، قم بمقارنة النتائج من أجل التعرف على جوهر المشكلة ككل.
الطرق الأكثر شيوعًا لإعداد البيانات الأولية هي:
-
التقييس ؛
-
القياس (النطاق الافتراضي هو [0 ، 1]) ؛
-
التطبيعيمكن أتمتة هذه العمليات مع التقييم اللاحق ووضعها على الناقل باستخدام أداة
خطوط الأنابيب .
مقتطف الشفرة مع توحيد البيانات المصدر كما يلي:
لاحظ إضافة "_SS" (اختصار لـ StandardScaler) إلى قائمة الأسماء. يتم ذلك حتى لا تتراكم النتائج ، وكذلك لعرضها بسهولة باستخدام "مدير متغير" بعد إجراء التحويلات.
يؤدي تشغيل مقتطف الشفرة إلى الحصول على النتائج التالية:
SS_LR: train = 0.958 (0.015) / test = 0.949 SS_LDA: train = 0.951 (0.014) / test = 0.946 SS_KNN: train = 0.968 (0.023) / test = 0.970 SS_CART: train = 0.853 (0.036) / test = 0.835 SS_NB: train = 0.756 (0.046) / test = 0.751 SS_LSVC: train = 0.945 (0.018) / test = 0.941 SS_SVC: train = 0.976 (0.015) / test = 0.990 SS_MLP: train = 0.976 (0.012) / test = 0.973 SS_BG: train = 0.947 (0.018) / test = 0.948 SS_RF: train = 0.973 (0.016) / test = 0.970 SS_ET: train = 0.980 (0.012) / test = 0.975 SS_AB: train = 0.827 (0.049) / test = 0.823 SS_GB: train = 0.964 (0.013) / test = 0.968
صندوق الشارب (StandardScaler):
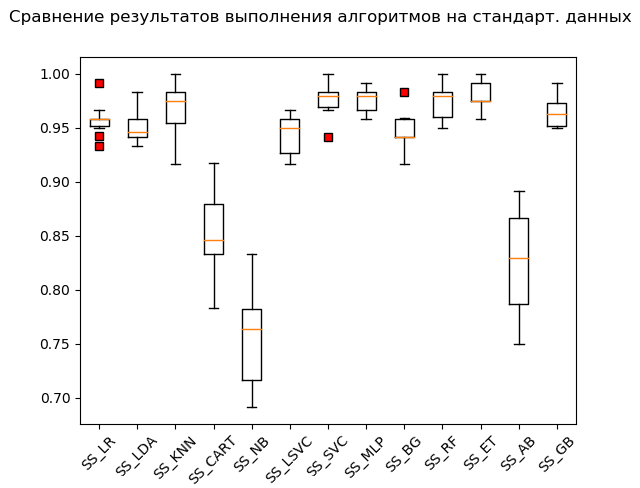
وفقًا لنتائج الحساب على البيانات الموحدة ، أصبحت الخوارزميات التالية رائدة:
SS_SVC: train = 0.976 (0.015) / test = 0.990 SS_ET: train = 0.980 (0.012) / test = 0.975 SS_MLP: train = 0.976 (0.012) / test = 0.973 SS_KNN: train = 0.968 (0.023) / test = 0.970 SS_RF: train = 0.973 (0.016) / test = 0.970 SS_GB: train = 0.964 (0.013) / test = 0.968 SS_LR: train = 0.958 (0.015) / test = 0.949 SS_BG: train = 0.947 (0.018) / test = 0.948 SS_LDA: train = 0.951 (0.014) / test = 0.946 SS_LSVC: train = 0.945 (0.018) / test = 0.941 SS_CART: train = 0.853 (0.036) / test = 0.835 SS_AB: train = 0.827 (0.049) / test = 0.823 SS_NB: train = 0.756 (0.046) / test = 0.751
كما يقولون ، من الخرق إلى الثروات: طريقة متجه الدعم ('SVC') ، التي تغذيها بيانات موحدة ، فعلت الباقي ، مما أدى إلى نتيجة ممتازة. أثناء الفحص "اليدوي" ، ومقارنة قيم المتغيرات
Y_test و
Forecastions_SS [6] ، لم تمضغ الخوارزمية سوى عدد قليل من القيم.
بعد ذلك ، يتم تنفيذ نفس الرمز لوظائف MinMaxScaler (التحجيم) و Normalizer (التطبيع). لن أعطي الرمز الكامل في المقال. يمكنك تنزيله من مستودع التخزين الخاص بي على GitHub:
link .
فقط تذكر أن تتدلى لفترة من الوقت وتضحك على "للأغراض التعليمية فقط"! :)
نتيجة لذلك ، بعد الاطلاع على الكود بالكامل ، نحصل على النتائج التالية:
LR: train = 0.957 (0.014) / test = 0.948 LDA: train = 0.951 (0.014) / test = 0.946 KNN: train = 0.985 (0.013) / test = 0.981 CART: train = 0.843 (0.033) / test = 0.830 NB: train = 0.819 (0.048) / test = 0.806 LSVC: train = 0.942 (0.017) / test = 0.928 SVC: train = 0.343 (0.079) / test = 0.342 MLP: train = 0.972 (0.012) / test = 0.961 BG: train = 0.952 (0.021) / test = 0.941 RF: train = 0.968 (0.017) / test = 0.965 ET: train = 0.980 (0.010) / test = 0.975 AB: train = 0.827 (0.049) / test = 0.823 GB: train = 0.964 (0.013) / test = 0.968 SS_LR: train = 0.958 (0.015) / test = 0.949 SS_LDA: train = 0.951 (0.014) / test = 0.946 SS_KNN: train = 0.968 (0.023) / test = 0.970 SS_CART: train = 0.853 (0.036) / test = 0.835 SS_NB: train = 0.756 (0.046) / test = 0.751 SS_LSVC: train = 0.945 (0.018) / test = 0.941 SS_SVC: train = 0.976 (0.015) / test = 0.990 SS_MLP: train = 0.976 (0.012) / test = 0.973 SS_BG: train = 0.947 (0.018) / test = 0.948 SS_RF: train = 0.973 (0.016) / test = 0.970 SS_ET: train = 0.980 (0.012) / test = 0.975 SS_AB: train = 0.827 (0.049) / test = 0.823 SS_GB: train = 0.964 (0.013) / test = 0.968 MMS_LR: train = 0.961 (0.013) / test = 0.953 MMS_LDA: train = 0.951 (0.014) / test = 0.946 MMS_KNN: train = 0.985 (0.013) / test = 0.981 MMS_CART: train = 0.850 (0.027) / test = 0.840 MMS_NB: train = 0.796 (0.045) / test = 0.786 MMS_LSVC: train = 0.964 (0.012) / test = 0.958 MMS_SVC: train = 0.963 (0.016) / test = 0.956 MMS_MLP: train = 0.972 (0.011) / test = 0.963 MMS_BG: train = 0.948 (0.024) / test = 0.946 MMS_RF: train = 0.973 (0.014) / test = 0.968 MMS_ET: train = 0.983 (0.010) / test = 0.981 MMS_AB: train = 0.827 (0.049) / test = 0.823 MMS_GB: train = 0.963 (0.013) / test = 0.968 N_LR: train = 0.938 (0.020) / test = 0.919 N_LDA: train = 0.952 (0.013) / test = 0.949 N_KNN: train = 0.981 (0.012) / test = 0.985 N_CART: train = 0.834 (0.028) / test = 0.825 N_NB: train = 0.825 (0.043) / test = 0.805 N_LSVC: train = 0.960 (0.014) / test = 0.953 N_SVC: train = 0.551 (0.053) / test = 0.586 N_MLP: train = 0.963 (0.018) / test = 0.946 N_BG: train = 0.949 (0.016) / test = 0.938 N_RF: train = 0.973 (0.015) / test = 0.970 N_ET: train = 0.982 (0.012) / test = 0.980 N_AB: train = 0.825 (0.040) / test = 0.820 N_GB: train = 0.953 (0.022) / test = 0.956
نتائج "أفضل 5":
SS_SVC: train = 0.976 (0.015) / test = 0.990 N_KNN: train = 0.981 (0.012) / test = 0.985 KNN: train = 0.985 (0.013) / test = 0.981 MMS_KNN: train = 0.985 (0.013) / test = 0.981 MMS_ET: train = 0.983 (0.010) / test = 0.981
وبالتالي ، وفقًا لنتائج اختبار بدء التشغيل لخوارزميات التعلم الآلي لحل مشكلة تصنيف مجموعة البيانات "الأرقام" ، فإن خوارزميات التعلم الآلي الأكثر ملاءمة هي: طريقة k -قرب الجيران ("KNN") وطريقة متجه الدعم ('SVC') والأشجار الإضافية ( 'ET). ينبغي إيلاء هذه الخوارزميات عن كثب مزيدًا من التطوير للنتائج التي تهدف إلى زيادة كفاءة العمليات الحسابية. كل شيء ، كما يقولون ، قابل للحل.
وعلى هذه المذكرة المرفوعة ، تابع بسلاسة إلى الجزء الثاني.
مشكلة التنبؤ
نتحرك على الإبهام:
قم بتشغيل الكود والتعامل مع القاموس. الوصف والمفاتيح كالتالي:
نقوم بتعيين المفتاح "بيانات" إلى المتغير
X ، وهو عبارة عن صفيف NumPy متعدد الأبعاد مع مجموعة من السمات ، وصفوف البعد 506 في 13 عمودًا ، والمتغير
Y - "الهدف" ، صفيف NumPy متعدد الأبعاد مع علامة لكل صف.
نقسم مجموعة البيانات إلى أجزاء تدريب واختبار ، ونقوم بتكوين المعلمات لتقييم الخوارزميات. في المعلمة "تسجيل النتائج" ، قمنا بتعيين أحد
المقاييس 'r2' التقليدية لتحليل الانحدار:
R2 - معامل التحديد - هذه هي نسبة تباين المتغير التابع ، موضحة في النموذج المعني (
رابط ).
"يأخذ معامل التحديد للنموذج ذو الثابت قيمًا من 0 إلى 1. كلما كان المعامل أقرب إلى 1 ، كلما كانت التبعية أقوى. عند تقييم نماذج الانحدار ، يتم تفسير ذلك على أنه مطابق للنموذج مع البيانات. بالنسبة للنماذج المقبولة ، من المفترض أن يكون معامل التحديد على الأقل 50٪ (في هذه الحالة ، يكون معامل الارتباط المتعدد يتجاوز معامل٪ 70). يمكن اعتبار النماذج ذات معامل التحديد أعلى من 80٪ جيدة (معامل الارتباط يتجاوز 90٪). إن مساواة معامل التحديد مع الوحدة تعني أن المتغير الموضح يتم وصفه بالضبط بواسطة النموذج قيد الدراسة " (المرجع نفسه).
لحل مشكلة التنبؤ ، نستخدم الخوارزميات التالية:
الخوارزميات الخطية:
-
الانحدار الخطي ('LR')
- الانحدار ريدج (الانحدار ريدج) /
الانحدار ريدج ('R')
- انحدار لاسو (من الإنجليزية LASSO - مشغل الانكماش والاختيار المطلق الأقل) /
انحدار لاسو ('L')
- طريقة
الانحدار الصافي المرن (ELN)
- طريقة
انحدار الزاوية الأقل (LARS) ("LARS")
- انحدار التلال البايزي / انحدار التلال
البايزي ('BR')
الخوارزميات غير الخطية:
- طريقة
k -قرب
الجيران regressor ('KNR')
-
شجرة القرار Regressor ('DTR')
-
آلة ناقلات الدعم الخطي (الانحدار) /
آلة ناقلات الدعم الخطي - الانحدار / ('LSVR')
- طريقة
متجه الدعم (الانحدار) /
انحدار متجه دعم إبسيلون ('SVR')
مجموعة الخوارزميات:
- AdaBoost (الانحدار) /
AdaBoost Regressor ('ABR') (AdaBoost = Boosting Boosting)
- التعبئة (الانحدار) /
أكياس التعبئة ('BR') (التعبئة = تجميع التمهيد)
-
الأشجار الإضافية Regressor ('ETR')
- تعزيز التدرج (الانحدار) /
تدرج تعزيز الانحدار ('GBR')
-
تصنيف الغابات العشوائي (الانحدار) /
مصنف الغابات العشوائي ('RFR')
وبالتالي ، فإن قائمة "النماذج" تحتوي على النماذج التالية:
models = [] models.append(('LR', LinearRegression())) models.append(('R', Ridge())) models.append(('L', Lasso())) models.append(('ELN', ElasticNet())) models.append(('LARS', Lars())) models.append(('BR', BayesianRidge(n_iter=n_iter))) models.append(('KNR', KNeighborsRegressor())) models.append(('DTR', DecisionTreeRegressor())) models.append(('LSVR', LinearSVR())) models.append(('SVR', SVR())) models.append(('ABR', AdaBoostRegressor(n_estimators=n_estimators))) models.append(('BR', BaggingRegressor(n_estimators=n_estimators))) models.append(('ETR', ExtraTreesRegressor(n_estimators=n_estimators))) models.append(('GBR', GradientBoostingRegressor(n_estimators=n_estimators))) models.append(('RFR', RandomForestRegressor(n_estimators=n_estimators)))
كما هو الحال مع التصنيف ، يتم تقييم فعالية كل خوارزمية باستخدام التحقق من الصحة. تحتوي الرسالة المعروضة على المعلومات التالية: يتم عرض اسم النموذج في شكل اختصار ، ومتوسط درجة التحقق المتبادل ذي العشرة أضعاف على بيانات التدريب (المقياس 'r2') ، والانحراف المعياري ومعامل التحديد r2 على بيانات الاختبار بين قوسين.
بعد تشغيل الكود ، نحصل على النتائج التالية:
LR: train = 0.746 (0.068) / test = 0.579 R: train = 0.744 (0.067) / test = 0.570 L: train = 0.689 (0.070) / test = 0.641 ELN: train = 0.677 (0.074) / test = 0.662 LARS: train = 0.744 (0.069) / test = 0.579 BR: train = 0.739 (0.069) / test = 0.571 KNR: train = 0.434 (0.288) / test = 0.538 DTR: train = 0.671 (0.145) / test = 0.637 LSVR: train = 0.550 (0.144) / test = 0.459 SVR: train = -0.012 (0.048) / test = -0.003 ABR: train = 0.810 (0.078) / test = 0.763 BR: train = 0.854 (0.064) / test = 0.805 ETR: train = 0.889 (0.047) / test = 0.836 GBR: train = 0.878 (0.042) / test = 0.863 RFR: train = 0.852 (0.068) / test = 0.819
مخطط سبان:
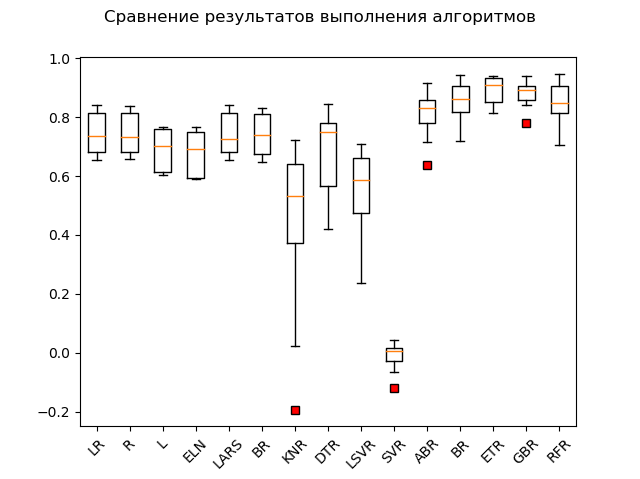
القادة الواضحون هم طرق الفرقة "GBR" (التدرج "التعزيز") ، "ETR" (الأشجار الإضافية) ، "RFR" (الغابة العشوائية) و "BR" ("التعبئة"):
GBR: train = 0.878 (0.042) / test = 0.863 ETR: train = 0.889 (0.047) / test = 0.836 RFR: train = 0.852 (0.068) / test = 0.819 BR: train = 0.854 (0.064) / test = 0.805 ABR: train = 0.810 (0.078) / test = 0.763 ELN: train = 0.677 (0.074) / test = 0.662 L: train = 0.689 (0.070) / test = 0.641 DTR: train = 0.671 (0.145) / test = 0.637 LR: train = 0.746 (0.068) / test = 0.579 LARS: train = 0.744 (0.069) / test = 0.579 BR: train = 0.739 (0.069) / test = 0.571 R: train = 0.744 (0.067) / test = 0.570 KNR: train = 0.434 (0.288) / test = 0.538 LSVR: train = 0.550 (0.144) / test = 0.459 SVR: train = -0.012 (0.048) / test = -0.003
واحد "adabust" ، "loshara" نوعا ما ، متخلفة.
ربما يقوم القادة الثلاثة بتمشيط التقييس والتطبيع. لنكتشف ذلك عن طريق تنفيذ بقية الكود.
النتائج هي كما يلي:
SS_LR: train = 0.746 (0.068) / test = 0.579 SS_R: train = 0.746 (0.068) / test = 0.578 SS_L: train = 0.678 (0.054) / test = 0.510 SS_ELN: train = 0.665 (0.060) / test = 0.513 SS_LARS: train = 0.744 (0.069) / test = 0.579 SS_BR: train = 0.746 (0.066) / test = 0.576 SS_KNR: train = 0.763 (0.098) / test = 0.739 SS_DTR: train = 0.610 (0.242) / test = 0.629 SS_LSVR: train = 0.727 (0.091) / test = 0.482 SS_SVR: train = 0.653 (0.126) / test = 0.610 SS_ABR: train = 0.811 (0.076) / test = 0.819 SS_BR: train = 0.853 (0.074) / test = 0.813 SS_ETR: train = 0.887 (0.048) / test = 0.846 SS_GBR: train = 0.878 (0.038) / test = 0.860 SS_RFR: train = 0.851 (0.071) / test = 0.818 N_LR: train = 0.751 (0.099) / test = 0.576 N_R: train = 0.287 (0.126) / test = 0.271 N_L: train = -0.030 (0.032) / test = -0.000 N_ELN: train = -0.007 (0.030) / test = 0.023 N_LARS: train = 0.751 (0.099) / test = 0.576 N_BR: train = 0.744 (0.100) / test = 0.589 N_KNR: train = 0.485 (0.192) / test = 0.504 N_DTR: train = 0.729 (0.080) / test = 0.765 N_LSVR: train = 0.182 (0.108) / test = 0.136 N_SVR: train = 0.086 (0.076) / test = 0.084 N_ABR: train = 0.795 (0.053) / test = 0.752 N_BR: train = 0.854 (0.054) / test = 0.827 N_ETR: train = 0.877 (0.048) / test = 0.850 N_GBR: train = 0.852 (0.063) / test = 0.872 N_RFR: train = 0.852 (0.051) / test = 0.801
كما ترون ، أساليب الفرقة لا تزال أمام الجميع."أعلى 5" يحتوي على النتائج التالية: N_GBR: train = 0.852 (0.063) / test = 0.872 GBR: train = 0.878 (0.042) / test = 0.863 SS_GBR: train = 0.878 (0.038) / test = 0.860 N_ETR: train = 0.877 (0.048) / test = 0.850 SS_ETR: train = 0.887 (0.048) / test = 0.846
:
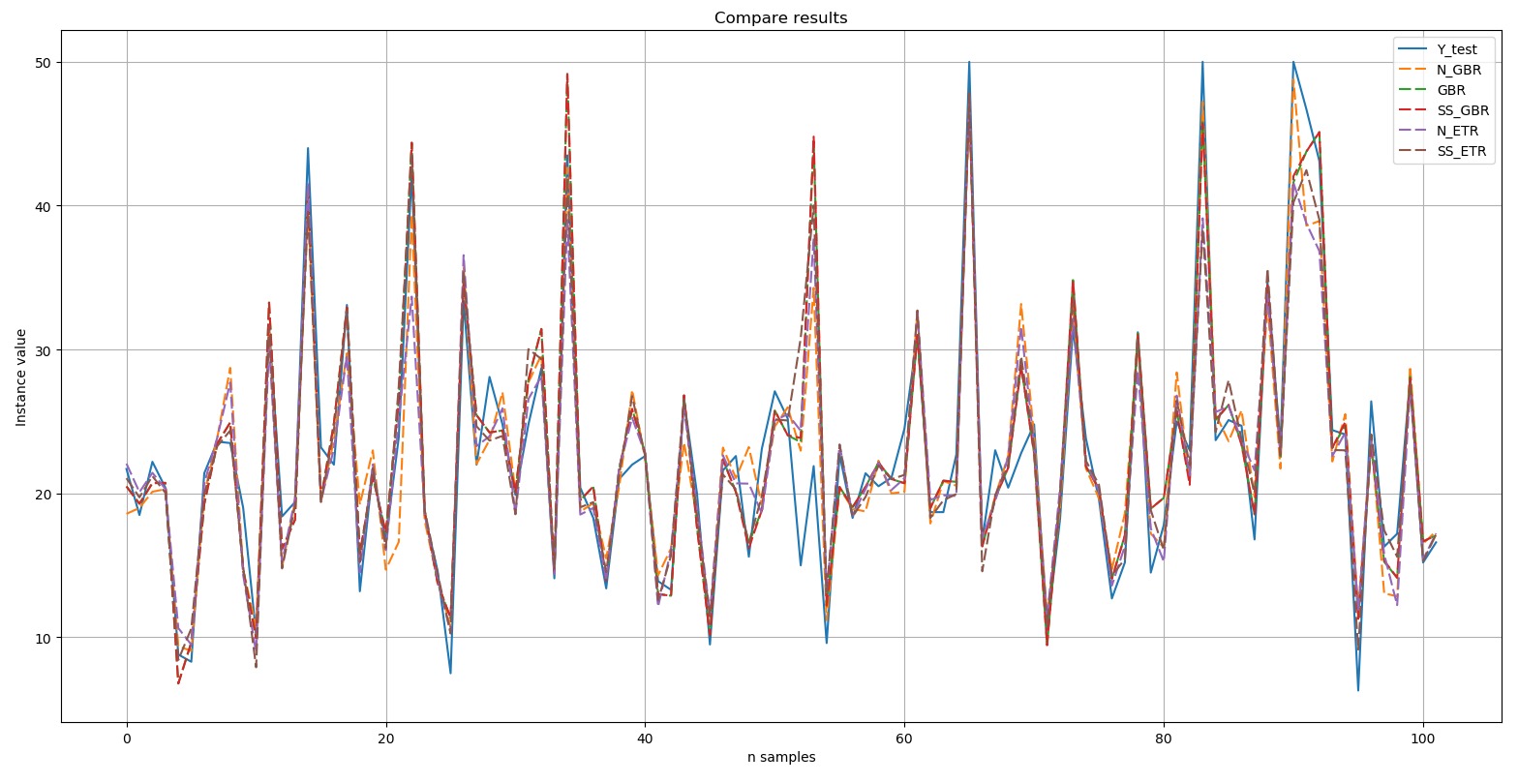Y-test – . , , (dashed). , , .
, Top 5:
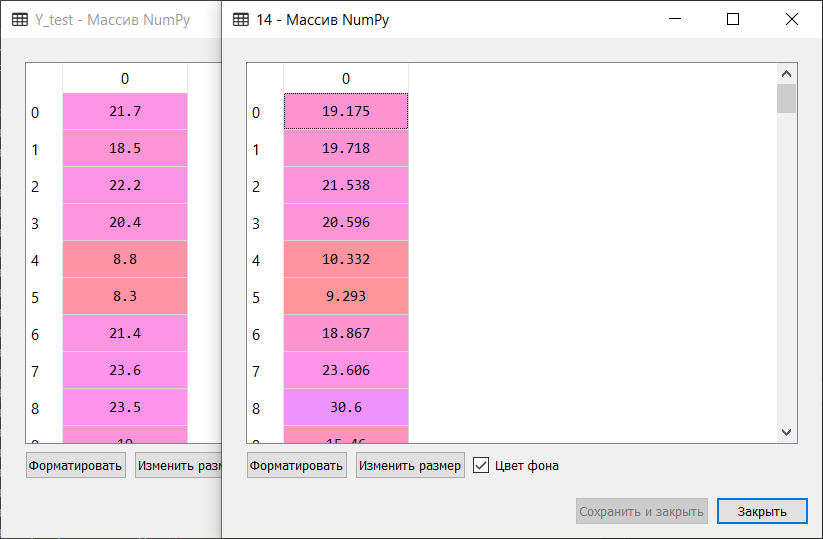
, - 'boston house-price' «» ('GBR') - ('ETR'). .
خاتمة
- (). , 'digits', 10 , 'boston house-price', «» «» .
, , GitHub. :
.
— -. , : . :)
. , , , . , «- », , , , ( ):), ; , ; , «». :)
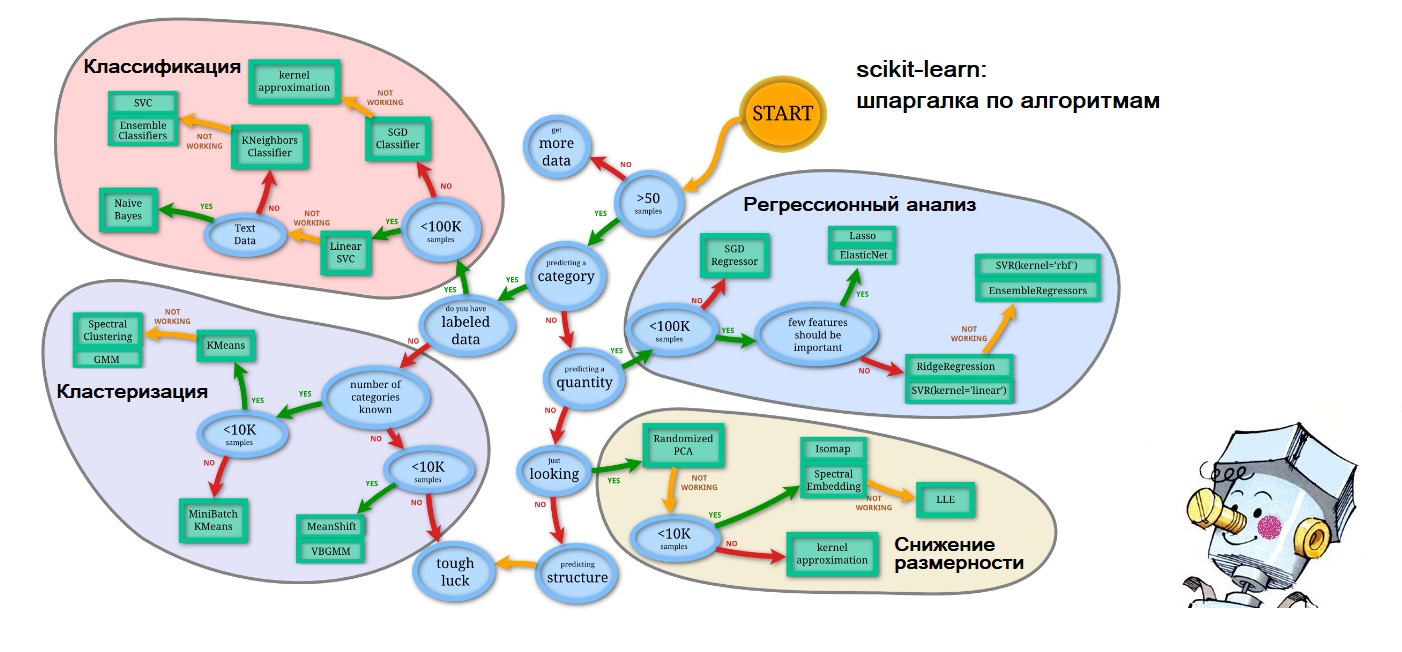
PS , , - : scikit-learn.org (
'Choosing the right estimator' ):
. – .