فرضية التوأم الرئيسي هي واحدة من القضايا الأكثر أهمية وتعقيدا في الرياضيات. حل اثنان من علماء الرياضيات نسخة موازية من هذه المشكلة للأنظمة العددية الصغيرة.

في 7 سبتمبر ،
نشر اثنان من علماء الرياضيات
دليلا على نسخة من واحدة من أكثر المشاكل المفتوحة شهرة في الرياضيات. تفتح النتيجة جبهة جديدة في دراسة فرضية
الأعداد الأولية المزدوجة التي ابتليت بها علماء الرياضيات لأكثر من مائة عام وترتبط ببعض من أكثر الخصائص عميقة في الحساب.
وقال
جيمس ماينارد ، عالم الرياضيات من جامعة أكسفورد: "لقد انحرفنا لفترة طويلة ونفاد الأفكار لهذه المهمة ، لذا فمن الطبيعي أن يكون لدى شخص ما أفكار جديدة".
تنطبق فرضية التوأم الأساسي على أزواج من الأعداد الأولية التي تختلف بمقدار 2. والتوأم هما الأعداد 5 و 7. و 17 و 19. تنص الفرضية على وجود عدد لا حصر له من هذه الأزواج بين الأعداد الطبيعية. على مدار العقد الماضي ، أحرز علماء الرياضيات تقدماً ملحوظاً ، لكنهم ما زالوا بعيدين عن الحل الكامل للمشكلة.
أثبت مؤلفو الدليل الجديد ،
ويل سافين من جامعة كولومبيا
ومارك شوسترمان من جامعة ويسكونسن في ماديسون ، فرضية عالم رياضيات أصغر ، لكن لا يزال ملحوظًا. لقد أثبتوا صلاحيتها في حالة وجود نظام عددي محدود حيث لا يوجد سوى عدد قليل من الأرقام.
تسمى أنظمة الأرقام هذه "الحقول المحدودة". على الرغم من صغر حجمها ، إلا أنها تحتفظ بالعديد من الخصائص الرياضية الملازمة لعدد صحيح لا يحصى. يحاول علماء الرياضيات إيجاد إجابات لأسئلة الحساب في الحقول المحدودة ، ويأملون في ترجمة هذه النتائج إلى جميع الأعداد الصحيحة.
وقال ماينارد: "إن الحلم النهائي ، وإن كان ساذجًا بعض الشيء ، هو أن الفهم الجيد لخصائص الحقل المحدود يمكن أن يلقي الضوء على عالم الأعداد الصحيحة".
بالإضافة إلى إثبات فرضية الأعداد الأولية المزدوجة ، وجد Savin و Shusterman نتيجة أكثر إثارة للدهشة فيما يتعلق بسلوك الأعداد الأولية في الأنظمة العددية الصغيرة. لقد أثبتوا مدى تواتر ظهور الأعداد الأولية المزدوجة على فترات صغيرة - وهذه النتيجة تجعل من الممكن التحكم بدقة شديدة في ظاهرة مثل الأعداد الأولية المزدوجة. يحلم علماء الرياضيات بتحقيق نتائج مماثلة بأعداد عادية ؛ انهم يستكشفون أدلة جديدة في البحث عن الأفكار التي تنطبق على الأعداد الأولية على خط الأرقام.
نوع جديد من البرايم
التنبؤ الأكثر شهرة لفرضية التوأم الرئيسي هو وجود عدد كبير لا حصر له من أزواج من الأرقام التي تختلف بمقدار 2. ومع ذلك ، فإن هذا البيان هو أكثر عمومية. تقول أن هناك عددًا لا حصر له من الأعداد الأولية التي تختلف عن 4 (على سبيل المثال ، 3 و 7) ، أو 14 (293 و 307) ، أو عن طريق أي رقم تحدده.
اتخذ Alfons de Polignac
هذا الافتراض في شكله الحديث في عام 1849. خلال السنوات الـ 160 القادمة ، لم يتقدم علماء الرياضيات معه كثيرًا. ومع ذلك ، في عام 2013 ، كسر الجليد ، أو على الأقل تصدع بشكل خطير. في تلك السنة ، أثبت
تشانغ إيثان وجود عدد كبير لا حصر له من أزواج الأعداد الأولية ، والتي لا تزيد عن 70 مليونًا ، وفي العام المقبل ، قام علماء الرياضيات الآخرون ، بمن فيهم ماينارد
وتيري تاو ، بتقليل هذه الفجوة بشكل خطير. السجل الحالي هو دليل على وجود عدد كبير لا حصر له من أزواج الأعداد الأولية التي تختلف عن بعضها البعض بما لا يزيد عن 246.
ومع ذلك ، بعد ذلك ، تراجع التقدم. يفهم علماء الرياضيات الحاجة إلى فكرة جديدة تمامًا لحل هذه المشكلة بالكامل. وأنظمة الأعداد المحدودة هي مكان جيد للبحث عن هذه الفكرة.
لإنشاء حقل محدود ، تحتاج أولاً إلى استخراج مجموعة فرعية محددة من الأرقام من الأرقام الطبيعية. يمكنك ، على سبيل المثال ، أن تأخذ الأرقام الخمسة الأولى (أو أي رقم أولي). وبدلاً من تمثيل الأرقام على سطر الأرقام ، كالمعتاد ، تخيل نظام أرقام جديد في شكل قرص.
الحساب ، كما قد تفكر ، يبدأ في العمل في مكان محصور. ماذا سيكون 4 + 3 في نظام عددي محدود يتكون من خمسة عناصر؟ نبدأ بالرقم 4 ، ونحسب ثلاثة أقسام في اتجاه عقارب الساعة ، ونصل إلى 2. ونعمل الطرح والضرب والقسمة بطريقة مماثلة.

ولكن فقط هناك الصيد. في الحقول المحدودة ، لا يكون التعريف المعتاد للقيمة الأولية منطقيًا. في الحقل الأخير ، يتم تقسيم أي عدد على أي عدد آخر. على سبيل المثال ، 7 غير قابلة للقسمة عادةً على 3. ولكن في الحقل الأخير المكون من خمسة عناصر ، يمكن تقسيمها. ذلك لأن الرقم 7 في هذا الحقل النهائي يعادل الرقم 12 - كلاهما ينتهي عند علامة 2 من الاتصال الهاتفي. لذلك ، فإن 7 مقسومة على 3 سوف تعطي نفس قيمة 12 مقسومة على 3 - و 12 مقسمة على 3 تعطي 4.
لذلك ، تشير فرضية الأعداد الأولية المزدوجة للحقول المحدودة إلى كثيرات الحدود البسيطة - مثل التعبيرات الرياضية مثل x
2 + 1 على سبيل المثال.
لنفترض ، على سبيل المثال ، أن الحقل الأخير يحتوي على الأرقام 1 و 2 و 3. وستكون هذه الأرقام هي معاملات كثيرة الحدود في هذا الحقل المحدود ، وسيكون متعدد الحدود "بسيط" واحدًا لا يمكن تحليله إلى عوامل متعددة الحدود. لذلك ، ستكون x
2 + x + 2 بسيطة ، حيث لا يمكن معالجتها ، لكن x
2 - 1 لن: هذا هو منتج (x + 1) و (x - 1).
بعد تحديد كثيرات الحدود البسيطة ، من الطبيعي أن نسأل سؤالًا حول كثيرات الحدود الثنائية البسيطة - أزواج من كثيرات الحدود بسيطة وتختلف بقيمة ثابتة. على سبيل المثال ، متعدد الحدود x
2 + x + 2 بسيط ، مثل x
2 + 2x + 2. يختلف عن x.
تشير فرضية كثيرات الحدود الثنائية البسيطة للحقول المحدودة إلى وجود عدد كبير لا حصر له من أزواج متعددة الحدود البسيطة التي تختلف ليس فقط عن طريق x ، ولكن بأي قيمة.
تخفيضات أنيق
قد تبدو مفاهيم الحقول المحدودة وحدود متعددة بسيطة بعيدة المنال ، وغير مجدية لدراسة خصائص الأرقام. لكنها تبدو وكأنها محاكي للأعاصير - كون بحد ذاته يعطي أفكارًا عن الظواهر التي تحدث في عالم كبير.
"هناك تشابه قديم بين الأعداد الصحيحة وتعدد الحدود ، والذي يسمح لك بتحويل المشاكل المعقدة للغاية المحتملة المتعلقة بالأعداد الصحيحة إلى مهام متعلقة بالعديد من الحدود ، والتي من المحتمل أيضًا أن تكون معقدة ، ولكن قد يكون حلها أسهل ،" قال Shusterman.
أصبحت الحقول المحدودة مشهورة في عام 1940 عندما طور
Andre Weil الطريقة الدقيقة لترجمة حساب أنظمة الأعداد الصغيرة إلى حساب الأعداد الصحيحة. وايل تستخدم هذا الصدد مع نتائج مذهلة. لقد
أثبت ، ربما ، المشكلة الأكثر أهمية في الرياضيات - فرضية ريمان - بالنسبة للحالة مع مجموعة من المنحنيات على الحقول المحدودة (تعرف هذه المشكلة باسم فرضية ريمان الهندسية). هذا الدليل ، إلى جانب مجموعة من
فرضيات Weyl الإضافية
، جعل الحقول المحدودة مشهدًا غنيًا للاكتشافات الرياضية.
كانت فكرة ويل الأساسية أنه في الحقول المحدودة ، يمكن استخدام التقنيات الهندسية للعثور على إجابات لأسئلة حول الأرقام. هذه سمة من سمات الحقول المحدودة. قال شوسترمان: "يمكن إعادة صياغة العديد من المهام التي تريد حلها هندسيًا".
لفهم كيفية ظهور الهندسة في مثل هذه البيئة ، تخيل كل حدود متعددة كنقطة في الفضاء. تخدم معاملات كثير الحدود كإحداثيات تحدد موقعها. بالعودة إلى مجالنا النهائي وهو 1 و 2 و 3 ، يقع متعدد الحدود 2x + 3 عند النقطة (2 ، 3) من الفضاء ثنائي الأبعاد.
ولكن حتى في أبسط مساحة محدودة ، يوجد عدد لا حصر له من كثير الحدود. كثير الحدود المعقدة يمكن أن تنشأ عن طريق زيادة الأس الأس الأكبر ، أو درجة التعبير. في حالتنا ، سيتم تمثيل متعدد الحدود x
2 - 3x - 1 بنقطة في الفضاء ثلاثي الأبعاد. وسيتم تمثيل متعدد الحدود 3x
7 + 2x
6 + 2x
5 - 2x
4 - 3x
3 + x
2 - 2x + 3 بنقطة في الفضاء ذي الأبعاد الثمانية.
في هذا العمل الجديد ، تمثل هذه المساحة الهندسية جميع الحدود متعددة الحدود لدرجة معينة في مجال محدد. يتحول السؤال إلى ما يلي: هل هناك طريقة لعزل كل النقاط التي تشير إلى كثيرات الحدود البسيطة؟
استراتيجية Savin و Shusterman هي تقسيم المساحة إلى جزأين. في جزء واحد ، سيكون هناك كل النقاط المقابلة للعديد الحدود مع عدد من العوامل. في الجانب الآخر ، كل النقاط المقابلة لعدد الحدود مع عدد فردي من العوامل.
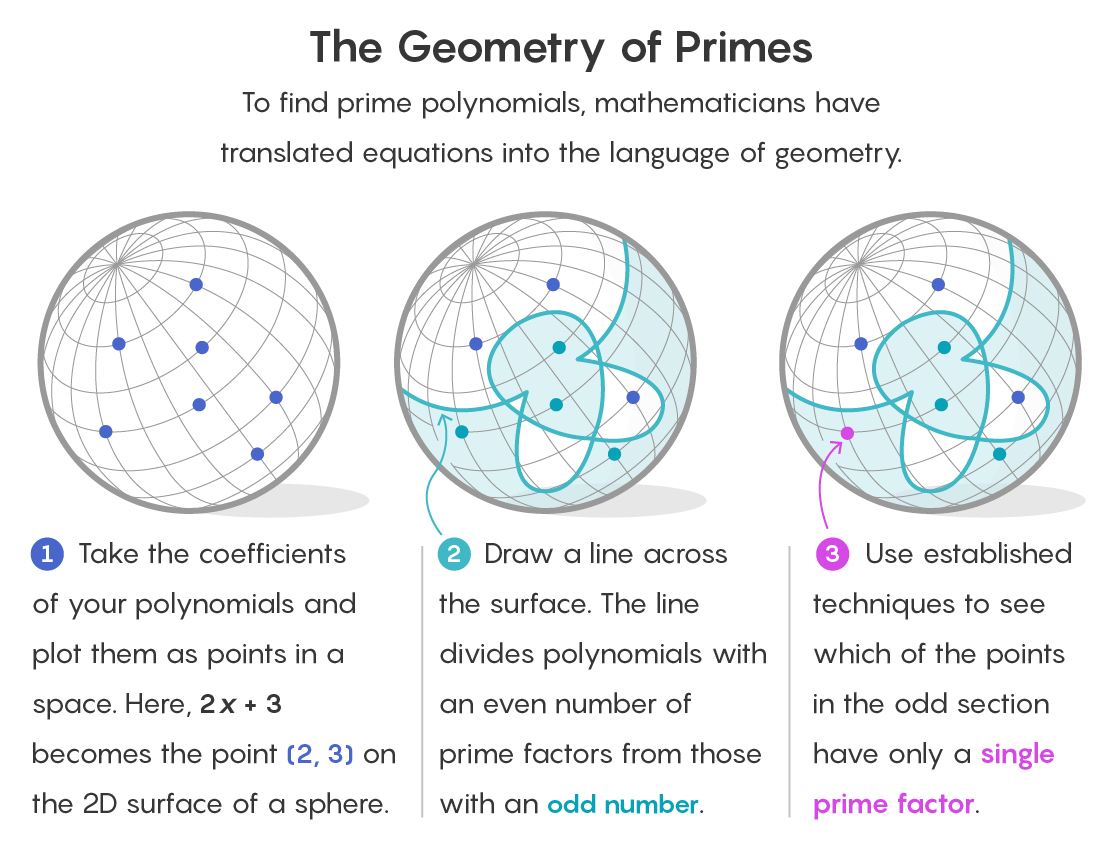
هذا يبسط بالفعل المهمة. تنطبق فرضية كثيرات الحدود الثنائية البسيطة للحقول المحدودة فقط على كثيرات الحدود بعامل واحد (تمامًا مثل العامل الأول له عامل واحد ، فهو نفسه). ونظرًا لأن الرقم 1 غريب ، يمكن على الفور تجاهل جزء من المساحة التي تحتوي على كثير الحدود مع عدد زوجي من العوامل.
الحيلة هي استخدام الانقسام. في حالة كائن ثنائي الأبعاد ، على سبيل المثال ، سطح الكرة ، يتم قطعه إلى النصف بواسطة منحنى أحادي البعد - تمامًا كما يقطع خط الاستواء سطح الأرض. يمكن دائمًا قطع كائن ذي عدد كبير من الأبعاد بكائن يقل عدد الأبعاد عن الآخر.
لكن هذه الأشكال ذات أبعاد أقل ، التي تقسم مساحة كثيرات الحدود ، ليست أنيقة على الإطلاق مثل خط الاستواء. يتم رسمها وفقًا لمعادلة رياضية تسمى
وظيفة Mobius . عند المدخل ، يأخذ متعدد الحدود ، وعند الناتج يعطي 1 إذا كان متعدد الحدود يحتوي على عدد زوجي من العوامل الأولية ، -1 إذا كان لديه رقم فردي ، و 0 إذا تم معاملته (حيث يمكن تحليل 16 إلى 2 × 2 × 2 × 2).
تنحني المنحنيات التي رسمتها وظيفة Mobius وتلتفت إلى الجنون ، وتتقاطع مع نفسها في أماكن كثيرة. يصعب بشكل خاص تحليل هذه الأماكن ، التي تسمى التفردات (تتوافق مع كثيرات الحدود التي يمكن أن تتحلل إلى عدة عوامل أولية متطابقة).
كان الابتكار الأساسي لدى Savin و Shusterman هو أنهم وجدوا الطريقة الدقيقة لقص الحلقات مع قياسات أقل إلى شرائح أقصر. كانت هذه الأجزاء أسهل في التعلم من الحلقة بأكملها.
بعد تجميع كتالوج متعدد الحدود مع عدد فردي من العوامل الأولية - وكان هذا هو الأصعب - واجه سافين وشوسترمان مع مهمة تحديد أيهما بسيط وأيهما توأمان. للقيام بذلك ، طبقوا العديد من الصيغ المستخدمة من قبل علماء الرياضيات لدراسة الأعداد الأولية بين تلك العادية.
استخدم Savin و Shusterman أسلوبهما لإثبات نقطتين مهمتين فيما يتعلق متعددو الحدود البسيطة في بعض المجالات المحدودة.
أولاً ، إن فرضية الأعداد الأولية المزدوجة في الحقول المحدودة صحيحة: فهناك عدد لا حصر له من أزواج كثيرات الحدود الثنائية التي تختلف بأي قيمة معينة.
ثانياً ، والأهم من ذلك ، يوفر هذا العمل عددًا دقيقًا لعدد متعددات الحدود البسيطة التي يمكن العثور عليها بين كثيرات الحدود بترتيب معين. يشبه ذلك معرفة عدد الأعداد الأولية المزدوجة الموجودة داخل أي فاصل زمني طويل بما فيه الكفاية على خط الأرقام - وهذا مجرد حلم علماء الرياضيات.
وقال زيف رودنيك من جامعة تل أبيب: "هذا هو العمل الأول الذي يعطي تشابهاً كمياً لما ينبغي أن يكون صحيحاً بالنسبة للأعداد الصحيحة ، وهذه نتيجة رائعة حقًا". "حتى الآن ، لم يحدث شيء مثل هذا."
يُظهر دليل Savin و Schusterman كيف ، بعد مرور 80 عامًا تقريبًا على إثبات Andre Weil فرضية ريمان للمنحنيات على الحقول المحدودة ، لا يزال علماء الرياضيات يتحركون بعناد في هذا الاتجاه. الآن ، سوف يتحول علماء الرياضيات الذين يتعاملون مع فرضية التوأم الرئيسيين إلى عمل Savin و Shusterman ، وربما سيمنحهم مصدرًا عميقًا للإلهام.