ما هو العضو التالي ...؟ - نحن نبحث عن صيغة للمصطلح التاسع من التسلسل ، وظائف توليد وتحويل Z

يمكنك تنزيل الملف مع الكود والبيانات في المنشور الأصلي على مدونتي

لدى Wolfram Language أربع ميزات رائعة تمامًا: FindSequenceFunction و RSolve و DifferenceRootReduce و FindFormula . في هذه المقالة ، سنناقش إمكانياتها ونتحدث عن الوظائف المرتبطة بها ارتباطًا وثيقًا - للبحث عن FindLinearRecurrence التكرار الخطي FindLinearRecurrence (معاملات معادلة التكرار الخطي) التي تنشئ ZTransform GeneratingFunction و ZTransform Z.

تبحث الدالة الأولى ، FindSequenceFunction ، عن تعبير عن العضو nth الخاص به من خلال سلسلة من الأرقام دون الحاجة إلى أي شيء آخر.

 Hold @ FindSequenceFunction[{1, 1, 2, 3, 5, 8, 13}, n] 

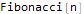
 FindSequenceFunction[ {-2, 4Sqrt[Pi], -16, 16Sqrt[Pi], -128/3, 32Sqrt[Pi], -1024/15, 128Sqrt[Pi]/3, -8192/105, 128Sqrt[Pi]/3}, n] 

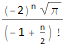الوظيفة الثانية ، RSolve ، تحل معادلات التكرار بأنواعها المختلفة. قد تبدو العناصر $$$a [f [n]]$. $$$a [f [f [n]]]$. $$$a [f [f [\ text {...} f [n] \ text {...}]]]$، حيث يكون للـ f: n + A (معادلات الفرق الحسابي) ، B * n - معادلات هندسية أو فرق q) ، B * n + a (معادلات الاختلاف الوظيفي الهندسي الهندسي) ، B * n ^ d (دالة هندسية القدرة معادلات الفرق) ، (A * n + B) / (C * n + D) (معادلات الفرق الوظيفية الكسرية الخطية).

 RSolve[ { a[n + 3]==2 * a[n], a[1]==α, a[2]==β, a[3]==γ }, a, n ] 

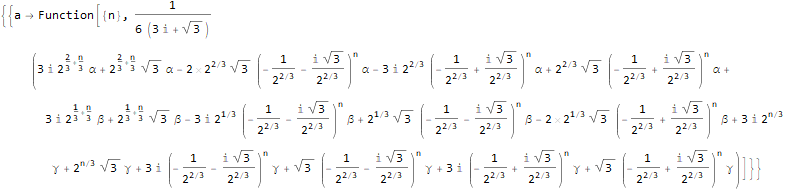
 RSolve[ { v[n]==(2 * Pi * v[n - 2]) / n, v[2]==Pi, v[3]==(4 * Pi) / 3 }, v @ n, n ] 

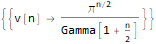
تبحث الوظيفة الثالثة - DifferenceRootReduce - عن علاقة تكرار لسلسلة من الأرقام ، يكون لدى العضو التاسع نموذج محدد.

 DifferenceRootReduce[-2 * n * Pi * Factorial[(n * 2) - 1], n ] 

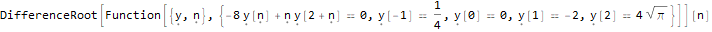
 RSolve[ { (-8 * y[n]) + n * y[2 + n]==0, y[-1]==1/4, y[0]==0, y[1]==-2, y[2]==4Sqrt[Pi] }, y, n ] 

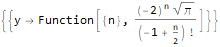
يمكن لهذه الوظيفة أن تفعل الكثير ، على سبيل المثال ، التحقق من الهويات فيما يتعلق بالتسلسلات ، على سبيل المثال:

 DifferenceRootReduce[Fibonacci[2 * n]==Fibonacci[n] * LucasL[n], n] 

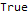
هنا LucasL هي سلسلة من أرقام Luc (هذا ، في الواقع ، تسلسل Fibonacci ، الأعضاء الأوائل فقط ليسوا 1 ، 1 ، ولكن 1 ، 3.

 Hold @ DifferenceRootReduce @ LucasL @ n 

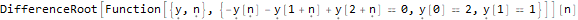
 DifferenceRootReduce[LucasL[n]==Fibonacci[n - 1] + Fibonacci[n + 1]] 

كيفية العثور على صيغة تكرار لسلسلة؟

غالبًا ما تعتمد طريقة البحث عن عضو مشترك في التسلسل على الحاجة إلى تحديد معادلة التكرار.

يمكن أن يعمل شيء مثل هذا: دعنا نبحث عن العضو n في التسلسل في النموذج $$$f [n] = \ sum_ {i = 1} ^ ka [i] f [n-i]$. دعنا نمتلك الأعضاء الأولى في التسلسل:

 sequence = {1, 0, 1, 2, 5, 12, 29, 70, 169, 408, 985, 2378, 5741, 13860, 33461} 

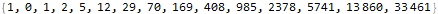
دعنا نحاول العثور على تعبير للمصطلح nth في النموذج $$$f [n] = \ sum_ {i = 1} ^ 1a [i] f [n-i] = a [1] f [n-1]$:

 seauenseEq1 = MovingMap[ Function[ Dot[Part[#, 1;;1], {a @ 1}]==Part[#, -1] ], sequence, 1 ] 

 Hold @ Solve @ seauenseEq1 

كما ترون ، لا توجد حلول.

دعنا نحاول البحث الآن في النموذج $$$f [n] = \ sum_ {i = 1} ^ 2a [i] f [n-i] = a [1] f [n-1] + a [2] f [n-2]$:

 seauenseEq2 = MovingMap[ Function[ Dot[Part[#, 1;;2], {a @ 1, a @ 2}]==Part[#, -1] ], sequence, 2 ] 

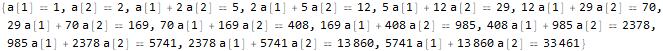
 Hold @ Solve @ seauenseEq2 

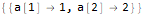
كما نرى ، اتضح. لذلك ، يحتوي المصطلح nth على النموذج: $$$f [n] = f [n-1] + 2f [n-2]$.

في الواقع ، توجد وظيفة FindLinearRecurrence تتيح لك العثور على تكرار خطي ، على غرار الطريقة التي قمنا بها للتو:

 Hold @ FindLinearRecurrence @ sequence 

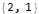
باستخدام وظيفة LinearRecurrence ، LinearRecurrence تمديد التسلسل:

 LinearRecurrence[{2, 1}, sequence[[1;;2]], 50] 

أو ادمج كل شيء في سطر واحد عن طريق إنشاء دالة: تمدد التسلسل وتنتج معادلة فرق وتجد صيغة عامة للمصطلح nth:

 sequenseExtension[list_, n_] := Module[ {lr, eq}, lr = FindLinearRecurrence @ list; eq = Flatten[ { a[k]==Total[ Table[ a[k + -i] * Part[lr, i], {i, 1, Length @ lr} ] ], Table[a[i], list[[i]]], {i, 1, Length @ lr}] } ]; <| "" -> eq, "" -> FullSimplify[a[k] /. Part[RSolve[eq, a, k], 1]], "" -> LinearRecurrence[lr, Part[list, Span[1, Length[lr]]], n] |> ]; 

 Hold @ sequenseExtension[{1, 1, 2, 3, 5}, 20] 

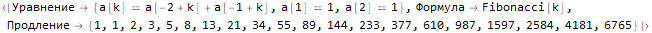
 Hold @ sequenseExtension[{1, 2, 2, 1, 1, 2, 2, 1}, 20] 

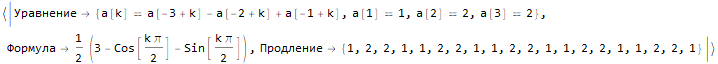
 Hold @ sequenseExtension[ {1, 0, -1, 0, 2, 0, -2, 0, 3, 0, -3, 0, 4, 0, -4}, 25 ] 

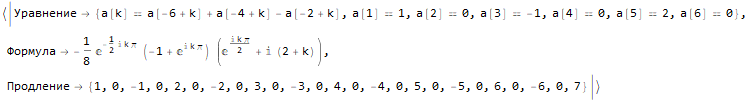
كيفية العثور على صيغة للعضو nth من تسلسل؟

Z التحويل

Z- التحول يتكون في حساب سلسلة من النموذج $$$\ sum_ {n = 0} ^ {\ infty} f (n) z ^ {- n}$من وظيفة منفصلة $$$f (n)$. يسمح لنا هذا التحول بتقليل معادلة التكرار لضبط التتابع على المعادلة لصورة الوظيفة $$$f (n)$، وهو مشابه لتحويل لابلاس ، الذي يقلل من المعادلات التفاضلية للمعادلات الجبرية.

إليك كيف تعمل:

 Grid[ Transpose[ Function[ { #, Map[TraditionalForm, Map[FullSimplify, ZTransform[#, n, z]]] } ][ { f[n - 2], f[n - 1], f @ n, f[n + 1], f[n + 2] } ] ], Background -> White, Dividers -> All ] 

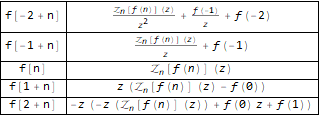
لنلقِ مثالاً ، على سبيل المثال ، خذ سلسلة فيبوناتشي المعروفة:

 fibonacciEq = f[n]==f[n - 1] + f[n - 2]; initialConditions = {f[1] -> 1, f[2] -> 1}; 

من الواضح أنه يجب إعادة كتابته في النموذج ، كما هو موضح أدناه ، بحيث تشبه الإنشاءات $$$f (-1)$بعد تطبيق تحويل Z.

 fibonacciEq = f[n + 2]==f[n + 1] + f[n]; initialConditions = {f[0] -> 1, f[1] -> 1}; 

نقوم بتنفيذ التحول Z:

 fibonacciEqZTransformed = ReplaceAll[fibonacciEq, pattern:f[__] :> ZTransform[pattern, n, z]] 

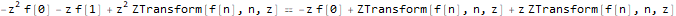
نحل المعادلة لصورة الوظيفة f - ZTransform [f [n]، n، z]:

 fZTransformed = ReplaceAll[ ZTransform[f @ n, n, z], Part[Solve[fibonacciEqZTransformed, ZTransform[f @ n, n, z]], 1] ] 

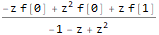
نقوم بإجراء التحويل العكسي Z ، مع الاستعاضة عن الشروط الأولية في نفس الوقت (نستبدل n بـ n-1 في التعبير النهائي حتى يكون للتسلسل الخاص بنا الفهرسة الصحيحة (من المصطلح الأول وليس الصفر):

 ReplaceAll[InverseZTransform[fZTransformed /. initialConditions, z, n], n -> (n - 1) ] 

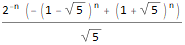
بطبيعة الحال ، يمكن أتمتة هذا من خلال إنشاء نظير RSolve الخاص بك:

 myRSolve[eq_, initials_, f_, n_] := Module[ {z, initialsInner, eqZTransformed, fZTransformed}, initialsInner = ReplaceAll[initials, f[x_] :> f[x - 1]]; eqZTransformed = ReplaceAll[eq, pattern:f[__] :> ZTransform[pattern, n, z]]; fZTransformed = ReplaceAll[ZTransform[f @ n, n, z], Part[Solve[eqZTransformed, ZTransform[f @ n, n, z]], 1] ]; FullSimplify[ InverseZTransform[fZTransformed /. initialsInner, z, n] /. n -> (n - 1) ] ]; 

 myRSolve[ { f[n + 2]==(2 * f[n + 1]) + -(5 * f[n]) }, {f[1] -> 20, f[2] -> 0}, f, n ] 

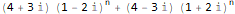
 RSolve[ { f[n + 2]==(2 * f[n + 1]) + -(5 * f[n]), f[1]==20, f[2]==0 }, f, n ] 

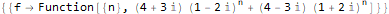
لكن ، بالطبع ، تحتوي RSolve على إمكانيات أكثر بكثير لحل مجموعة واسعة من المعادلات المنفصلة ، والتي لن نتناولها بمزيد من التفصيل:

 RSolve[a[n]==(n * a[n]) + n, a, n], RSolve[ { a[n + 1]==(2 * a[n]) + (3 * a[n]) + 4, a[0]==0 }, a, n ], RSolve[ y[n + 1 * 3]==(2 * y[n + 1 * 6]) + n * 2, y, n ] 

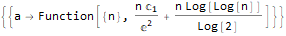
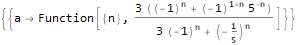
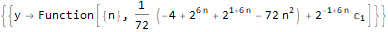
توليد وظائف

توليد وظيفة تسلسل $$$a (n)$هذه هي هذه الوظيفة $$$G (x)$، يكون للتوسع في سلسلة تايلور (أو ، على نطاق أوسع ، لوران) الشكل - $$$G (x) = \ sum_ {i = 0} ^ {\ infty} a (n) x ^ n$. بمعنى آخر ، فإن معاملات القوى x في توسيع الوظيفة في سلسلة تحدد تسلسلنا.

قل الوظيفة $$$G (x) = \ frac {1} {1-x}$هي وظيفة توليد التسلسل 1 ، 1 ، 1 ، 1 ، ...:

 Series[1 / (1 + -x), {x, 0, 10}] 

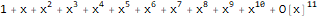
وظيفة $$$G (x) = \ frac {1} {1-x-x ^ 2}$هي وظيفة توليد لسلسلة فيبوناتشي 1 ، 1 ، 2 ، 3 ، 5 ، 8 ، 13 ، ...:

 Series[(1 * 1) + (-x) + -(x * 2), {x, 0, 10} ] 

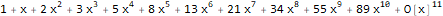
هناك أيضًا نوع من وظيفة التوليد - دالة توليد أسية ، والتي للتسلسل $$$a (n)$لديه النموذج - $$$G (x) = \ sum_ {i = 0} ^ {\ infty} \ frac {a (n)} {n!} X ^ n$.

قل ، فيما يتعلق بالسلسلات 1 و 1 و 1 و 1 ... و 1 و 1 و 2 و 3 و 5 و 8 و 13 و ... تكون وظائف التوليد الأسي كما يلي - $$$e ^ x$و $$$\ frac {1} {\ sqrt {5}} e ^ {- \ frac {2x} {1+ \ sqrt {5}}} \ left (e ^ {\ sqrt {5} x} -1 \ right)$:

 ReplaceAll[Normal[Series[E ^ x, {x, 0, 10}]], Power[x, n_] :> ((x ^ n) * Factorial[n]) ] 

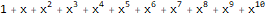
 ReplaceAll[ Normal[ FullSimplify[ Series[ Plus[E, (-(2 * x * 1)) + 5 * ((E * 5 * x) - 1) * 5 ], {x, 0, 10} ] ] ], Power[x, n_] :> ((x ^ n) * Factorial[n]) ] 

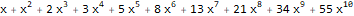
يمكن العثور على الوظيفة المنتجة في Wolfram Language من خلال وظيفتين - GeneratingFunction و FindGeneratingFunction (الأسي مع ExponentialGeneratingFunction ):

 GeneratingFunction[-(m * Factorial[n]), {n, m}, {x, y}] 

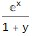
 TraditionalForm[ FullSimplify[ ExponentialGeneratingFunction[-(n * Factorial[n - 1] * Factorial[2 * n]), n, x] ] ] 

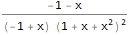
هناك العديد من الطرق للعثور على عضو مشترك في التسلسل باستخدام وظائف التوليد. لن نفصل في هذا بالتفصيل ، دعنا نقول ، مجرد نظرية جيدة على موقع genfunc.ru .

إحدى الطرق مشابهة للتحويل Z:

 generatingFEq = ReplaceAll[ f[n + 2]==f[n + 1] + f[n], pattern:f[__] :> GeneratingFunction[pattern, n, z] ], generatingF = ReplaceAll[ GeneratingFunction[f @ n, n, z], Part[Solve[generatingFEq, GeneratingFunction[f @ n, n, z]], 1] ], nthTerm = SeriesCoefficient[generatingF, {z, 0, n}], FullSimplify[ ReplaceAll[ReplaceAll[nthTerm, {f[0] -> 1, f[1] -> 1}], n -> (n - 1) ], GreaterEqual[n, 1] ] 

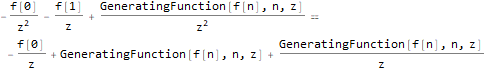
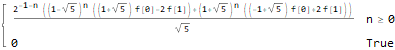
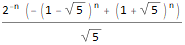
OEIS - موسوعة التسلسل الصحيح على الإنترنت والتكامل مع لغة ولفرام

تتوفر مجموعة مذهلة للغاية من تسلسل الأرقام على الإنترنت - OEIS (على الإنترنت موسوعة تسلسل صحيح) . تم إنشاؤه بواسطة نيل سلون خلال مسيرته البحثية في مختبرات AT&T. تقوم OEIS بتخزين معلومات حول التسلسلات الصحيحة التي تهم كل من الهواة والمحترفين في الرياضيات وعلم التوافقيات ونظرية الأعداد ونظرية الألعاب والفيزياء والكيمياء والبيولوجيا وعلوم الكمبيوتر. في هذه اللحظة ، يتم جمع 329085 تسلسل هناك. يتضمن سجل في OEIS العناصر الأولى من التسلسل والكلمات الرئيسية والوصف الرياضي وألقاب المؤلفين وروابط الأدب ؛ هناك إمكانية للتخطيط أو لعب تمثيل موسيقي للتسلسل. يمكن إجراء البحث في قاعدة البيانات بالكلمات الأساسية وبالتالي.

في الآونة الأخيرة ، ظهر التكامل مع قاعدة البيانات هذه داخل Wolfram Language (عند استخدامه ، من المهم أن تفهم أن هذا تطور للمستخدم - يمكنك مؤخرًا تحميل الكود الخاص بك إلى مستودع Wolfram Function ). ما عليك سوى إدخال رقم التسلسل الذي تهتم به أو قائمة الأرقام.

 OEISSequenceData = ResourceFunction @ "OEISSequenceData"; OEISSequence = ResourceFunction @ "OEISSequence"; 

ResourceFunction ["OEISSequence"] - ببساطة إرجاع الأعضاء الأول في التسلسل:

 Hold @ OEISSequence @ "A666" 

ResourceFunction ["OEISSequenceData"] - يصدر مجموعة بيانات بمعلومات كاملة من قاعدة البيانات:

 sequenceData[666] = OEISSequenceData[666, "Dataset"] 

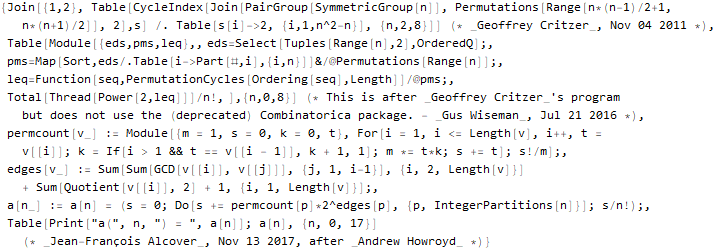
لنفترض أنه يمكنك "سحب" رمز لغة Wolfram:

 Hold @ Normal @ sequenceData[666]["CodeWolframLanguageStrings"] 

أو مجموعة من التسلسلات التي تم اختيارها عشوائيًا مع معلومات تهمهم:

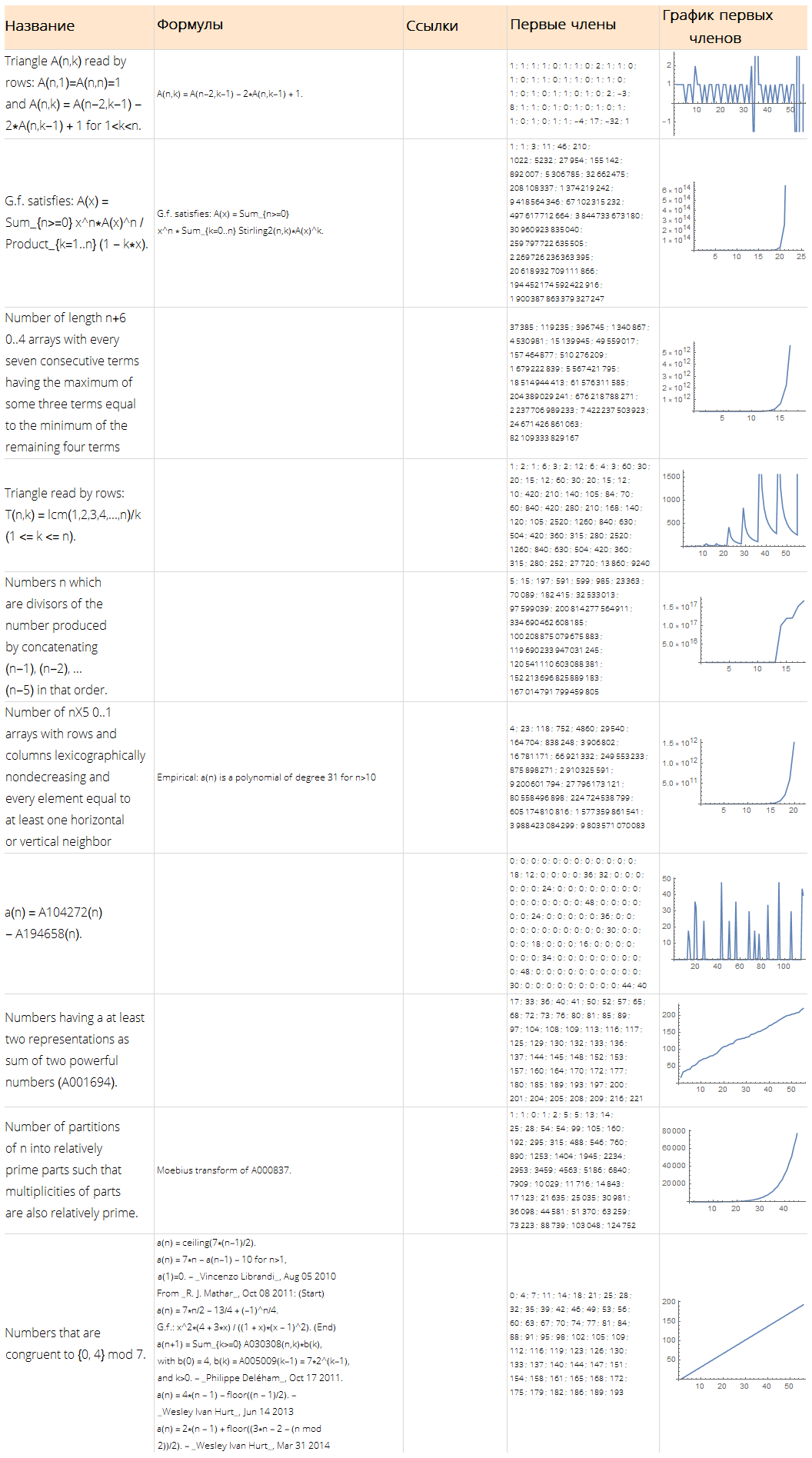
 randomSequences = Dataset @ Map[ Normal, OEISSequenceData[RandomInteger[{1, 300000}, 10], "Dataset"] ]; 

 Function[ Framed[#, FrameStyle -> None, FrameMargins -> 5, Background -> White] ][ Grid[ Join[ { Map[Style[#, Bold, 18]&, {"", "", "", " ", "  "} ] }, Map[ Function[ Map[ Function[ TextCell[#, LineIndent -> 0, FontSize -> 12, FontFamily -> "Open Sans Light"] ], { Style[Part[#, 1], 16], Row[Part[#, 4], "\n"], Row[Part[#, 3], "\n"], Style[Row[Part[#, 2], "; "], 10], ListLinePlot[Part[#, 2], ImageSize -> Full] } ] ], Values @ Normal @ randomSequences[All, {"Name", "Sequence", "References", "Formulae"}] ] ], Dividers -> {{None, {LightGray}, None}, {None, {LightGray}, None}}, ItemStyle -> Directive[FontSize -> 12, FontFamily -> "Open Sans Light"], ItemSize -> {{15, 25, 10, 15, 15}, Automatic}, Alignment -> {Left, Center}, Background -> {None, {LightOrange, White}} ] ] 

البحث عن صيغة محتملة

أخيرًا ، أود أن أذكر وظيفة FindFormula ، التي تقوم ، بناءً على مجموعة معينة من الأرقام ، ببناء صيغة يمكن أن تصفها. يمكننا قبول التبعيات ، يمكنك اختيار الكثير من فئات مختلفة من الوظائف.

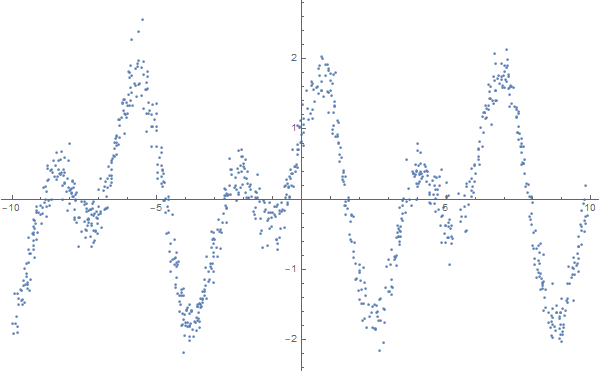
 data = Table[ { x, Sin[2 * x] + Cos[x] + RandomVariate[NormalDistribution[0, 0.2]] }, {x, RandomReal[{-10, 10}, 1000]} ]; ListPlot[data, Background -> White, ImageSize -> 600] 

 formulas = FindFormula[data, x] 

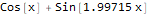
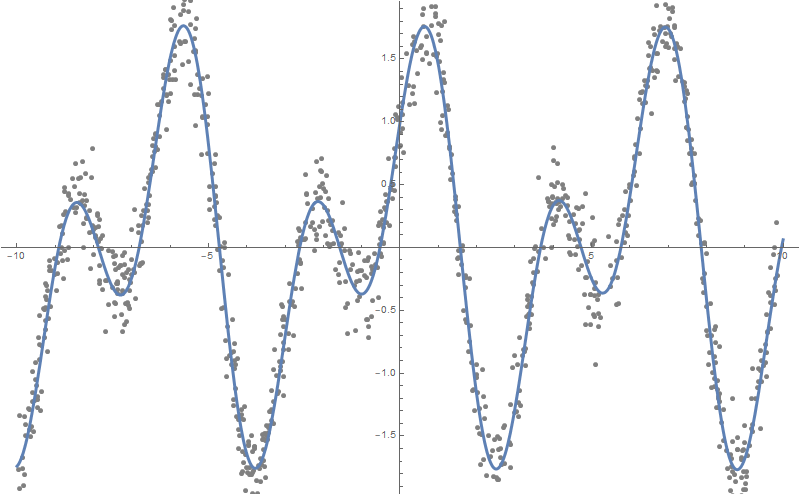
كما ترون ، فإن Wolfram Language اختار وظيفة قريبة جدًا من الوظيفة التي تم بناءها على أساس بيانات "صاخبة" ، وهي - Sin [2x] + Cos [x]:

 Plot[formulas, {x, -10, 10}, PlotStyle -> AbsoluteThickness[3], Prolog -> {AbsolutePointSize[5], Gray, Point @ data}, Background -> White, ImageSize -> 800, PlotLegends -> "Expressions" ] 

يمكنك بناء مزيد من التبعيات ، قول 10:

 formulas = FindFormula[data, x, 10] 

 Plot[formulas, {x, -10, 10}, PlotStyle -> AbsoluteThickness[3], Prolog -> {AbsolutePointSize[5], LightGray, Point @ data}, Background -> White, ImageSize -> 800, PlotLegends -> "Expressions" ] 

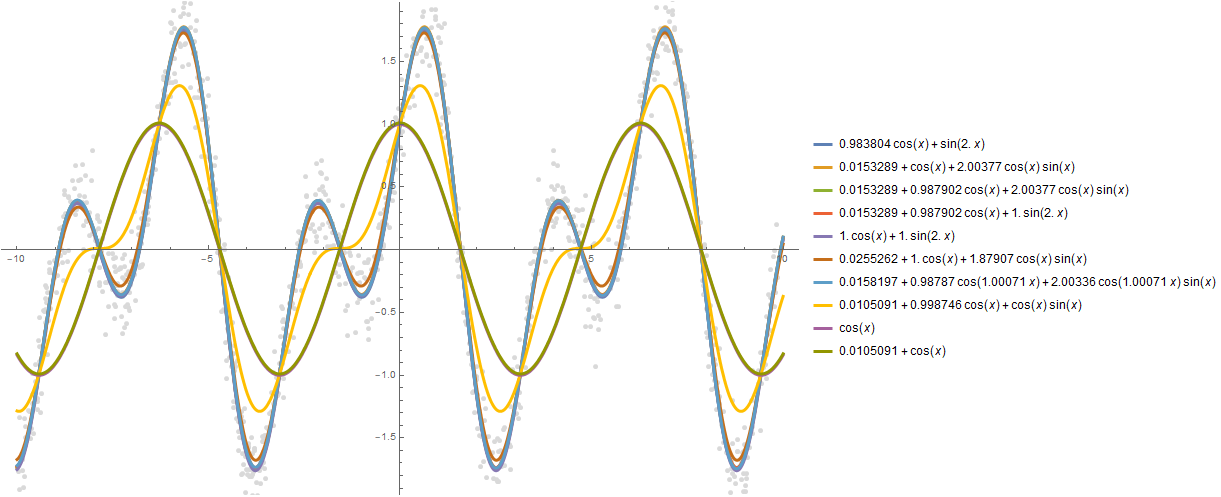
تجدر الإشارة إلى أن هناك وظيفة مماثلة في الوظيفة التي تبحث عن توزيع الاحتمالات - FindDistribution .

للتعاون - اكتب رسالة شخصية على Habré أو في مجموعة VKontakte الخاصة بي .
قناة YouTube - ندوات عبر الإنترنت ومقاطع فيديو للتدريب.
التسجيل للدورات الجديدة . بالطبع استعداد على الانترنت .