ماذا لو بدون بيثون؟ جوليا للتعلم الآلي وعموما

نريد دائمًا كتابة التعليمات البرمجية بسرعة ، ولكن عليك أن تدفع ثمنها. في اللغات العادية عالية المستوى المرنة ، يمكن تطوير البرامج بسرعة ، لكنها تعمل ببطء بعد الإطلاق. على سبيل المثال ، من البطيء قراءة شيء ثقيل في بيثون النقي. تعمل اللغات المشابهة لـ C بشكل أسرع بكثير ، لكن من السهل ارتكاب الأخطاء فيها ، حيث سيؤدي البحث عنها إلى تقليل كل مكاسب السرعة إلى لا شيء.

عادةً ما يتم حل هذه المعضلة على النحو التالي: أولاً يكتبون نموذجًا أوليًا على شيء مرن ، على سبيل المثال ، على Python أو R ، ثم يعيدون كتابته على C / C ++ أو Fortran. لكن هذه الدورة طويلة جدًا ، هل يمكنك الاستغناء عنها؟



ربما هناك حل. جوليا هي لغة برمجة عالية المستوى ومرنة وسريعة. جوليا لديها إيفاد متعددة ، مترجم الذكية وأدوات البرمجة metaprogramming. سيخبرك Gleb Ivashkevich ( phtRaveller ) ، مؤسس الرياضيات ، الذي يطور أنظمة تعلم الآلة للصناعة وغيرها من الصناعات ، وهو عالم فيزيائي سابق ، بمزيد من التفاصيل حول ما لدى جوليا.

سيشرح Gleb سبب الحاجة إلى لغات جديدة ولماذا تكون بايثون مفقودة في بعض الأحيان. سيقول لك ما هو مثير للاهتمام في جوليا ، حول نقاط قوتها وضعفها ، ومقارنتها باللغات الأخرى ، وإظهار ما لدى اللغة من إمكانية التعلم الآلي والحوسبة بشكل عام.

تنويه. لن يكون هناك تحليل لغوي. Habrazhiteli المطورين ذوي الخبرة ، لذلك لا معنى لإظهار كيفية كتابة حلقة ، على سبيل المثال.

مشكلة لغتين

إذا كتبت رمز سريع ، فستعمل البرامج ببطء. إذا كانت البرامج تعمل بسرعة ، فاكتبها لفترة طويلة.

بيثون الكلاسيكية تندرج في الفئة الأولى. إذا قمت بإزالة NumPy ، فكر في شيء في بيثون النقي ببطء. من ناحية أخرى ، هناك لغات مثل C و C ++. من الصعب إيجاد توازن ، وغالبًا ما يكتبون أولًا نموذجًا أوليًا عن شيء مرن ، وبعد تصحيح الخوارزمية ، يعيدون كتابته إلى اللغة بشكل أسرع. هذا مثال لمشكلة واضحة بلغتين : دورة طويلة عندما تضطر إلى الكتابة في بيثون ، وإعادة كتابتها في C أو في Cython ، على سبيل المثال.

المتخصصون في التعلم الآلي وعلوم البيانات لديهم NumPy ، Sklearn ، TensorFlow. لقد تم حل مشاكلهم لسنوات دون سطر واحد في C ، ويبدو أن مشكلة اللغتين لا تهمهم. هذا ليس صحيحًا ، فالمشكلة تتجلى بشكل ضمني ، لأن الكود في NumPy أو في TensorFlow ليس في الحقيقة بيثون. يتم استخدامه كقاعدة معدنية لإطلاق ما بداخله. الداخل هو بالضبط C / فورتران (في حالة NumPy) أو C ++ (في حالة TensorFlow).

هذه "الميزة" تكون ظاهرة بشكل سيئ ، على سبيل المثال ، في PyTorch ، ولكن في Numpy تكون مرئية بوضوح. على سبيل المثال ، إذا ظهرت دورة بيثون الكلاسيكية في الحسابات ، فقد حدث خطأ ما. في رمز الأداء ، ليست هناك حاجة إلى حلقات ؛ يجب عليك إعادة كتابة كل شيء حتى يتمكن NumPy من توجيهه وحسابه بسرعة.

في الوقت نفسه ، يبدو للكثيرين أن NumPy سريع وأن كل شيء على ما يرام. دعونا نرى ما لديه NumPy تحت غطاء محرك السيارة لرؤية هذا.

• يحاول NumPy حل مشكلة مرونة نوع Python ، لذلك يحتوي على نظام كتابة صارم . إذا كان للصفيف نوع معين ، فلا يمكن أن يكون هناك أي شيء آخر ؛ إذا كان Float64 ، فلا يمكن فعل شيء حيال ذلك.
• إيفاد. وفقًا لأنواع المصفوفات والعملية التي تحتاج إلى تنفيذها ، ستقرر NumPy بداخلها الوظيفة التي يجب الاتصال بها لإجراء الحسابات بأسرع ما يمكن. ستحاول المكتبة طرد Python الكلاسيكي من حلقة الحساب.

اتضح أن Numpy ليس بالسرعة التي يبدو عليها. هذا هو السبب في وجود مشاريع مثل Cython أو Numba . الأول يولد كود C من "الهجين" من بيثون و C ، والثاني يجمع الكود في بيثون وعادة ما يكون هذا أسرع.

إذا كان NumPy سريعًا كما يبدو للكثيرين ، فلن يكون لوجود Cython و Numba معنى.

نعيد كتابة كل شيء في Cython إذا أردنا العثور بسرعة على شيء كبير ومعقد. أحد المعايير لجودة الغلاف في Cython هو وجود أو عدم وجود مكالمات Python خالصة في الكود الذي تم إنشاؤه.

مثال بسيط: نضيف النوع (جيد) أو لا نضيف (سيئ) ، ونحصل على رمزين مختلفين تمامًا ، رغم أنه بالإضافة إلى الأنواع ، لا تختلف الخيارات الأولية.



عندما ننشئ كود C ، في الحالة الأولى نحصل على ما يلي:

 __pyx_t_4 = __pyx_v_i; __pyx_v_result = (__pyx_v_result + (*((double *) ( /* dim=0 */ (__pyx_v_a.data + __pyx_t_4 * __pyx_v_a.strides[0]) )))); 

وفي result =0. الثانية result =0. سوف تتحول إلى هذا:

 __pyx_t_6 = PyFloat_FromDouble((*((double *) ( /* dim=0 */ (__pyx_v_a.data + __pyx_t_4 * __pyx_v_a.strides[0]) )))); if (unlikely(!__pyx_t_6)) __PYX_ERR(0, 9, __pyx_L1_error) __Pyx_GOTREF(__pyx_t_6); __pyx_t_7 = PyNumber_InPlaceAdd(__pyx_v_result, __pyx_t_6); if (unlikely(!__pyx_t_7)) __PYX_ERR(0, 9, __pyx_L1_error) __Pyx_GOTREF(__pyx_t_7); __Pyx_DECREF(__pyx_t_6); __pyx_t_6 = 0; __Pyx_DECREF_SET(__pyx_v_result, __pyx_t_7); __pyx_t_7 = 0; 

عند تحديد نوع ما ، يتم تشغيل رمز C بسرعة البرق. إذا لم يتم تحديد النوع ، فسوف نرى Python عاديًا ، ولكن من الجانب C: مكالمات Python القياسية ، حيث يتم إنشاء float لسبب double ، ويتم حساب الروابط ، والكثير من أكواد البيانات المهملة الأخرى. هذا الرمز بطيء لأنه يستدعي Python لكل عملية.

هل من الممكن حل جميع المشاكل في وقت واحد

إنه أمر مضحك أنه عندما نفكر في شيء ما ، نحاول إزالة بيثون النقي. هناك خياران لكيفية القيام بذلك.

• باستخدام Cython أو غيرها من الأدوات. هناك العديد من الطرق التي يمكنك من خلالها تحسين شفرة Cython الخاصة بك حتى ينتهي الأمر بدون أي مكالمات من Python. لكن هذا ليس النشاط الأكثر متعة: ليس كل شيء واضحًا جدًا في Cython ، ولا يتم إنفاق سوى وقت أقل بقليل مما لو كنت تكتب كل شيء فقط في C. ليس من الواضح دائمًا كيفية تحسينه.
• باستخدام Numba ، الذي يقوم بتجميع JIT .

ولكن ربما هناك طريقة أفضل ، وأعتقد أن هذه هي جوليا .

جوليا

يدعي المبدعون أن هذه لغة سريعة وعالية المستوى ومرنة ، وهي مماثلة لبيثون من حيث سهولة كتابة التعليمات البرمجية. في رأيي ، تشبه Julia لغة البرمجة النصية: لست بحاجة إلى القيام بما عليك القيام به في لغة C ، حيث يكون كل شيء منخفض المستوى ، بما في ذلك هياكل البيانات. في الوقت نفسه ، يمكنك العمل في وحدة تحكم عادية ، مثل لغة Python واللغات الأخرى.

تستخدم جوليا مجموعة Just-In-Time - وهذا أحد العناصر التي تعطي السرعة. لكن اللغة جيدة في العمليات الحسابية ، لأنها وضعت من أجلهم. جوليا تستخدم للمهام العلمية والحصول على أداء لائق.

على الرغم من أن جوليا تحاول أن تبدو وكأنها لغة للأغراض العامة ، إلا أن جوليا جيدة للحوسبة وليست جيدة جدًا لخدمات الويب. إن استخدام Julia بدلاً من Django ، على سبيل المثال ، ليس هو الخيار الأفضل.

دعنا ننظر إلى ميزات اللغة كمثال لوظيفة بدائية.

 function f(x) α = 1 + 2x end julia> methods(f) # 1 method for generic function "f": [1] f(x) in Main at mpconf.jl:2 

هناك أربع ميزات ملحوظة في هذا الرمز.

• لا توجد أي قيود على استخدام Unicode . يمكنك أن تأخذ الصيغ من مقال عن التعلم العميق أو النمذجة العددية ، وإعادة كتابة بنفس الحروف ، وكل شيء سينجح - يونيكود مخيط في كل مكان تقريبًا.
• لا يوجد علامة الضرب. ومع ذلك ، ليس من الممكن دائمًا الاستغناء عنه ، على سبيل المثال ، بمقدار 2.x (عدد مرات الفاصلة العائمة x) ستقسم جوليا.
• لا return . بشكل عام ، من المستحسن أن تكتب return حتى تتمكن من رؤية ما يحدث ، ولكن المثال سيعود α ، لأن التعيين تعبير.
• لا أنواع . يبدو أنه إذا كان هناك سرعة ، ثم في مرحلة ما يجب أن تظهر الأنواع؟ نعم ، سوف تظهر ، ولكن في وقت لاحق.

جوليا لديها ثلاث ميزات تعطي المرونة والسرعة: إرسال متعددة ، metaprogramming والتوازي . سنتحدث عن الأولين ، ونترك التوازي للدراسة المستقلة للمستخدمين المتقدمين.

جدولة متعددة

تبدو الدعوة إلى methods(f) في المثال أعلاه بشكل غير متوقع - ما نوع الطرق التي تتبعها الوظيفة؟ لقد اعتدنا على حقيقة أن لدينا كائنات الطبقة ، الطبقات لديها أساليب. لكن في جوليا ، يتم تشغيل كل شيء من الداخل إلى الخارج: للوظائف طرق ، لأن اللغة تستخدم إرسال متعدد.

تعني الجدولة المتعددة أن متغير وظيفة معينة سيتم تنفيذه يتم تحديده من خلال مجموعة كاملة من أنواع المعلمات من هذه الوظيفة.

سوف أصف بإيجاز كيف يعمل هذا على مثال مألوف بالفعل.

 function f(x) α = 1 + 2x end function f(x::AbstractFloat) α = 1 + sin(x) end julia> methods(f) # 2 methods for generic function "f": [1] f(x::AbstractFloat) in Main at mpconf.jl:6 [2] f(x) in Main at mpconf.jl:2 

تسمى المتغيرات من نفس الوظيفة لمجموعات مختلفة من الأنواع الأساليب. هناك رمزان في الكود: الأول لكل أرقام الفاصلة العائمة ، والثاني لكل شيء آخر. عندما ندعو هذه الوظيفة لأول مرة ، ستقرر جوليا الطريقة التي يجب استخدامها وما إذا كنت تريد تجميعها. إذا كان قد تم بالفعل استدعاء وتجميعها ، فسوف يستغرق ذلك.

نظرًا لأن كل شيء في جوليا ليس هو ما اعتدنا عليه ، يمكنك هنا إضافة وظائف لأنواع معرفة من قبل المستخدم ، ولكن لن تكون هذه هي طرق الكتابة بمعنى OOP. سيكون ببساطة الحقل الذي تتم فيه كتابة الوظيفة ، لأن الوظيفة هي نفس الكائن الكامل مثل أي شيء آخر.

لمعرفة بالضبط ما سيتم تشغيله ، هناك وحدات ماكرو خاصة. يبدأون بـ @ . في المثال ، يسمح @which الماكرو @which بمعرفة الطريقة التي تم استدعاؤها لحالة معينة.



في الحالة الأولى ، قررت جوليا أنه نظرًا لأن 2 عددًا صحيحًا ، فإنه لا يناسب AbstractFloat ، ويسمى الخيار الأول. في الحالة الثانية ، قررت أنه كان Float وكانت قد دعت بالفعل للحصول على نسخة متخصصة. سيعمل هذا تقريبًا إذا قمت بإضافة طرق أخرى لبعض الأنواع المحددة.

LLVM و JIT

تستخدم جوليا إطار LLVM للترجمة. مكتبة تجميع JIT تأتي في حزمة لغة. في المرة الأولى التي تسمى فيها الوظيفة ، تتطلع جوليا لمعرفة ما إذا كانت الوظيفة قد استخدمت مع هذه المجموعة من الأنواع ، وتجميعها إذا لزم الأمر. سيستغرق الإطلاق الأول بعض الوقت ، ثم سيعمل كل شيء بسرعة.

سيتم تجميع الوظيفة في وقت الاستدعاء الأول لهذه المجموعة من المعلمات.

ميزات المترجم

• المترجم معقول بشكل معقول لأن LLVM منتج جيد.
• يمكن لمعظم المطورين المتقدمين النظر في عملية الترجمة ومعرفة ما يولدها.
• مجموعة جوليا ونومبا متشابهة . في Numba ، تقوم أيضًا بإنشاء ديكور JIT ، لكن في Numba لا يمكنك "الدخول" كثيرًا وتحديد ما يمكنك تحسينه أو تغييره.

لتوضيح عمل المترجم ، سأقدم مثالا على وظيفة بسيطة:

 function f(x) α = 1 + 3x end julia> @code_llvm f(2) define i64 @julia_f_35897(i64) { top: %1 = mul i64 %0, 3 %2 = add i64 %1, 1 ret i64 %2 } 

الماكرو @code_llvm يسمح لك بمشاهدة نتيجة الجيل. هذا LLVM IR هو تمثيل وسيط ، نوع من المجمّع.

في الكود ، يتم ضرب وسيطة الوظيفة بـ 3 ، 1 يضاف إلى النتيجة ، يتم إرجاع النتيجة. كل شيء واضح ومباشر قدر الإمكان. إذا قمت بتعريف الوظيفة بشكل مختلف قليلاً ، على سبيل المثال ، استبدل 3 بـ 2 ، ثم كل شيء سوف يتغير.

 function f(x) α = 1 + 2x end julia> @code_llvm f(2) define i64 @julia_f_35894(i64) { top: %1 = shl i64 %0, 1 %2 = or i64 %1, 1 ret i64 %2 } 

يبدو ، ما هو الفرق: 2 ، 3 ، 10؟ لكن جوليا و LLVM ترى أنه عند استدعاء دالة لعدد صحيح ، يمكنك القيام بذكاء أكبر. الضرب بواسطة عدد صحيح هو تحول يسار بمقدار بت واحد - إنه أسرع من المنتج. ولكن ، بالطبع ، هذا يعمل فقط للأعداد الصحيحة ، لن يعمل على تحويل Float اليسار بمقدار 1 بت والحصول على نتيجة الضرب في 2.

أنواع مخصصة

أنواع مخصصة في جوليا هي بأسرع أنواع المضمنة. يتم تنفيذ جدولة متعددة عليها ، وسوف تكون بالسرعة بالنسبة للأنواع المدمجة. وبهذا المعنى ، فإن آلية الإرسال المتعددة مضمنة بعمق في اللغة.

من المنطقي أن نتوقع أن المتغيرات لا تحتوي على أنواع ، والقيم لها فقط. المتغيرات بدون نوع هي مجرد علامة ، ملصق على بعض الحاوية.

نظام الكتابة هرمي. لا يمكننا إنشاء أحفاد من أنواع محددة ؛ يمكن أن تحتوي الأنواع المجردة عليها فقط. ومع ذلك ، لا يمكن إنشاء أنواع مجردة. وهذا فارق بسيط لن يروق للجميع.

كما أوضح مؤلفو اللغة عندما طوروا جوليا ، أرادوا الحصول على النتيجة ، وإذا كان من الصعب القيام بشيء ما ، فقد رفضوا ذلك. كان مثل هذا النوع من نظام التسلسل الهرمي أسهل لتطوير. هذه ليست مشكلة كارثية ، ولكن إذا لم تقم بإدارة رأسك للخارج في البداية ، فستكون غير مريحة.

يمكن تحديد أنواع المعلمات ، والتي تشبه إلى حد ما C / C ++. على سبيل المثال ، قد يكون لدينا هيكل توجد به حقول ، لكن أنواع هذه الحقول غير محددة - هذه معلمات. نحدد نوعًا محددًا عند إنشاء مثيل.

في معظم الحالات ، يمكن تخطي الأنواع . عادة ما تكون هناك حاجة إليها عندما يساعد النوع المترجم على تخمين أفضل طريقة للترجمة. في هذه الحالة ، من الأفضل تحديد الأنواع. تحتاج أيضًا إلى تحديد أنواع إذا كنت تريد تحقيق أداء أفضل.

دعونا نرى ما هو ممكن وما لا يمكن إنشاء مثيل له.



لا يمكن إنشاء مثيل للنوع الأول من AbstractPoint . هذا مجرد أصل مشترك لكل شخص يمكننا تحديده في الأساليب ، على سبيل المثال. يقول السطر الثاني أن PlanarPoint{T} هو سليل هذه النقطة المجردة. أسفل الحقول تبدأ - هنا يمكنك أن ترى المعلمة. يمكنك وضع float ، int أو نوع آخر هنا.

لا يمكن إنشاء مثيل للنوع الأول ، وبالنسبة للبقية فإنه من المستحيل إنشاء أحفاد. بالإضافة إلى ذلك ، افتراضيا فهي غير قابلة للتغيير . حتى تتمكن من تغيير الحقول ، يجب تحديد ذلك بشكل صريح.

عندما يكون كل شيء جاهزًا ، يمكنك المتابعة ، على سبيل المثال ، حساب المسافة لأنواع مختلفة من النقاط. في المثال ، النقطة الأولى على الطائرة هي PlanarPoint ، ثم على الكرة وعلى الاسطوانة. اعتمادًا على أي نقطتين نحسب المسافة بينهما ، نحتاج إلى استخدام طرق مختلفة. بشكل عام ، ستبدو الوظيفة بالشكل التالي:

 function describe(p::AbstractPoint) println("Point instance: $p") end 

بالنسبة إلى Float64 ، و Float64 ، و Float32 ، سيكون:

 function distance(pf::PlanarPoint{T}, ps::PlanarPoint{T}) where T<:AbstractFloat sqrt((pf.x-ps.x)^2 + (pf.y-ps.y)^2) end 

وبالنسبة للأعداد الصحيحة ، ستبدو طريقة حساب المسافة كما يلي:

 function distance(pf::PlanarPoint{T}, ps::PlanarPoint{T}) where T<:Integer abs(pf.x-ps.x) + abs(pf.y-ps.y) end 

بالنسبة للنقاط من كل نوع ، سيتم استدعاء أساليب مختلفة.



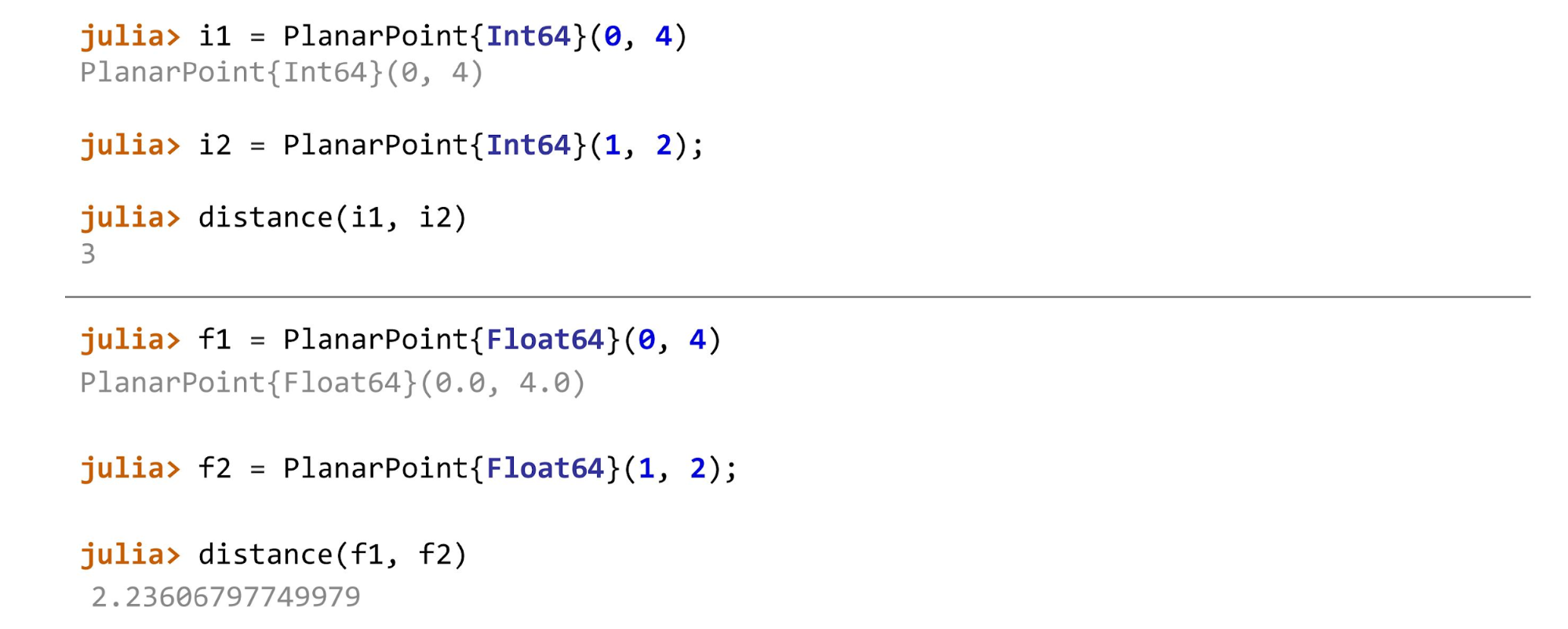
إذا قمت بالغش ، وعلى سبيل المثال ، قمت بتطبيق distance(f1, i2) ، ستقسم جوليا: "لا أعرف هذه الطريقة! لقد طلبت مني هذه الأساليب ، وقالت إنهم من نفس النوع. لم تخبرني كيف أحسب هذا عندما float معلمة واحدة والأخرى int . "

سرعة

ربما تكون قد سررت بالفعل: "هناك مجموعة JIT: الكتابة سهلة ، وسوف تعمل بسرعة. طرد بايثون وابدأ الكتابة في جوليا! "

لكن ليس بهذه البساطة. ليس كل ميزة في جوليا ستكون سريعة. ذلك يعتمد على عاملين.

• من المطور . لا توجد لغات تكون فيها أي وظيفة سريعة. سيقوم مطور عديم الخبرة بكتابة كود في C يعمل بشكل أبطأ من كود Python من مطور متمرس. أي لغة لها الحيل والفروق الدقيقة التي يعتمد عليها الأداء. المحول البرمجي ، سواء كان ثابتًا أو ثابتًا ، لا يمكن أن يوفر جميع الخيارات التي يمكن تصورها ويحسن كل شيء على الإطلاق.
• من نوع الاستقرار . في إصدار أسرع ، سيتم تجميع الوظائف المستقرة حسب النوع.

اكتب الاستقرار

ما هو نوع الاستقرار؟ عندما يتعذر على المحول البرمجي تخمين ما يحدث مع الأنواع بشكل كافٍ ، يجب أن يولد الكثير من التعليمات البرمجية للجمع بحيث يعمل كل شيء يصل إلى الإدخال.

مثال بسيط لفهم نوع الاستقرار.



سيقول متخصصو التعلم الآلي أن هذا تنشيط طبيعي للريلو: إذا كانت x> 0 ، فأعده كما هو ، وإلا فأرجع الصفر. مشكلة واحدة هي صفر بعد عدد صحيح علامة الاستفهام. هذا يعني أنه إذا قمنا باستدعاء هذه الوظيفة للحصول على رقم الفاصلة العائمة ، في حالة واحدة ، سيتم إرجاع رقم الفاصلة العائمة ، وفي عدد آخر ، عدد صحيح.

لا يمكن للمترجم تخمين نوع النتيجة فقط حسب نوع وسيطة الوظيفة. إنه يحتاج أيضًا إلى معرفة المعنى. لذلك ، فإنه يولد الكثير من التعليمات البرمجية.

بعد ذلك ، نقوم بإنشاء مجموعة من 100 لكل 100 رقم عشوائي من 0 إلى 1 ، ونحولها بمقدار 0.5 لتوزيع الأرقام الموجبة والسالبة بالتساوي ، وقياس النتيجة. هناك نقطتان مهمتان: النقطة والوظيفة. النقطة بعد rand(100,100) تعني "تنطبق على كل عنصر". إذا كان لديك نوع من التجميع والدالة العددية ، يمكنك وضع حد لها ، وستقوم جوليا بالباقي. يمكننا أن نفترض أن هذا فعال مثل حلقة عادية في لغة مترجمة طبيعية. لا حاجة للكتابة - سيتم القيام بكل شيء لك.

لا توجد مشاكل في هذه المرحلة - المشكلة هي داخل الوظيفة نفسها . الوقت المقدر لتنفيذ مثل هذا الخيار على جهاز كمبيوتر لائق لمثل هذه المصفوفة هو ميكروثانية. ولكن في الواقع - ميلي ثانية ، وهو الكثير لمثل هذه المصفوفة الصغيرة.

تغيير سطر واحد فقط.



تنشئ الدالة zero(x) صفرًا من نفس النوع مثل الوسيطة (x) . هذا يعني أنه بغض النظر عن قيمة x ، فسيكون نوع النتيجة دائمًا معروفًا بنوع x نفسه.

عندما ننظر إلى نوع الوسيطات فقط ونعرف نوع النتيجة بالفعل ، فهذه هي الدالات المستقرة للنوع.

إذا كنا بحاجة إلى إلقاء نظرة على معنى الحجج ، فهذه ليست وظائف مستقرة.

عندما يستطيع المحول البرمجي تحسين الكود ، يتم الحصول على الفرق في وقت التنفيذ عن طريق أمرين من الحجم. في المثال الثاني ، تم تخصيصه فقط إلى صفيف جديد ، بضع عشرات من وحدات البايت وليس أكثر. هذا الخيار أكثر فاعلية من الخيار السابق.

هذا هو الشيء الرئيسي الذي يجب الانتباه إليه عندما نكتب الكود في جوليا. إذا كتبت مثل في بيثون ، فستعمل كما في بيثون. إذا قمت بإجراء نفس العمليات على NumPy ، فلن يلعب الصفر مع أو بدون نقطة دورًا. لكن في جوليا ، يمكن أن يؤدي ذلك إلى تقويض الأداء إلى حد كبير.

لحسن الحظ ، هناك طريقة لمعرفة ما إذا كانت هناك مشكلة موجودة. هذا هو الماكرو @code_warntype ، والذي يسمح لك بمعرفة ما إذا كان المحول البرمجي يمكنه تخمين أين توجد الأنواع وتحسين ما إذا كان كل شيء على ما يرام.



في الخيار الأول (يسار) ، ليس المترجم متأكداً من النوع ويعرضه باللون الأحمر. في الحالة الثانية ، سيكون هناك دائمًا Float64 لمثل هذه الوسيطة ، بحيث يمكنك إنشاء رمز أقصر كثيرًا.

هذا ليس LLVM حتى الآن ، ولكن رمز جوليا المسمى ، return 0 أو return 0.0 يعطي فرق أداء من اثنين من أوامر الحجم.

metaprogramming

Metaprogramming هي عندما نقوم بإنشاء برامج في برنامج وتشغيلها أثناء التنقل.

هذه طريقة قوية تتيح لك القيام بالعديد من الأشياء المثيرة للاهتمام المختلفة. والمثال الكلاسيكي هو Django ORM ، الذي يقوم بإنشاء الحقول باستخدام metaclasses.

يعرف الكثير من الناس إخلاء المسؤولية من تيم بيترز مؤلف كتاب Zen of Python: "Metaclasses هي سحر أعمق لا ينبغي أن يقلق 99٪ من المستخدمين عنه. إذا كنت تتساءل ما إذا كانت هناك حاجة إلى نظارات في بيثون ، فأنت لست بحاجة إليها. إذا كنت في حاجة إليها ، فأنت تعرف بالضبط لماذا وكيفية استخدامها. "

مع metaprogramming ، يكون الوضع مشابهًا ، لكن في جوليا يكون مخيطًا بشكل أعمق ، وهذه ميزة مهمة للغة بأكملها. كود جوليا هو نفس هيكل البيانات مثل أي هيكل آخر ، يمكنك التعامل ، والجمع ، وإنشاء التعبيرات ، وكل هذا سوف ينجح.

 julia> x = 4; julia> typeof(:(x+1)) Expr julia> expr = :(x+1) :(x + 1) julia> expr.head :call julia> expr.args 3-element Array{Any,1}: :+ :x 1 

وحدات الماكرو هي واحدة من أدوات metaprogramming في جوليا : نوفر لهم شيئًا ما ، يبحثون ، نضيف الأداة المناسبة ، نزيل ما هو غير ضروري ، ونعطي النتيجة. في جميع الأمثلة السابقة ، قمنا بتمرير الاستدعاء إلى الوظيفة ، وقام الماكرو داخل التحليل بإجراء المكالمة. كل هذا يحدث على مستوى العمل مع شجرة بناء الجملة.

يمكنك تحليل تعبيرات بسيطة للغاية: إذا كانت ، على سبيل المثال ، (x+1) ، فهذه عبارة عن استدعاء للدالة + (الإضافة ليست عامل تشغيل ، كما هو الحال في العديد من اللغات الأخرى ، ولكنها دالة) ووسيطتين: حرف واحد (تعني النقطتان حرفًا ) ، والثاني هو مجرد ثابت.

مثال الماكرو بسيط آخر:

 macro named(name, expr) println("Starting $name") return quote $(esc(expr)) end end julia> @named "some process" x=5; Starting some process julia> x 5 

باستخدام وحدات الماكرو ، على سبيل المثال ، يتم إنشاء مؤشرات التقدم أو المرشحات لإطارات البيانات - وهذه آلية شائعة في جوليا.

لا يتم تنفيذ وحدات الماكرو في وقت المكالمة ، ولكن عند تحليل الرمز.

هذه هي ميزة الماكرو الرئيسية في جوليا. - , . , , .

,

Julia — . .

• Julia . .
• , . , , C .
• Julia JIT- . , , , , .
• — . .
• ( ). , . , , .
• Julia — .

النظام البيئي

, , Julia . , , data science , , , Python. , Python Pandas, , , , Julia .

Julia , Python 2008 . Python, , Julia. , . , Julia.

( ) Python Julia

. Julia: , , .…

. .

• DataFrames.jl .
• JuliaDB , .
• Query.jl . Pandas — - , ..

Plotting . Matplotlib , Julia. : VegaLite.jl , Plots.jl , , Gadfly.jl .

. TensorFlow , Flux.jl. Flux , , , Keras TensorFlow, . .

Scikit-learn . , , sklearn, , .

XGBoost . , Julia .

?

Jupyter . IDE — Juno, Visual Studio, .

. GPU/TPU . CUDAnative.jl Julia . Julia-, - , . , , , , .

: C, Fortran, Python .

, .

Packaging : Julia: , , ..

, , . , , . , PyTorch , TensorFlow, , .

, , , . Julia, , , . , , Zygote.jl . Flux.jl.

 julia> using Zygote julia> φ(x) = x*sin(x) julia> Zygote.gradient(φ, π/2.) (1.0,) julia> model = Chain(Dense(768, 128, relu), Dense(128, 10), softmax) julia> loss(x, y) = crossentropy(model(x), y) + sum(norm, params(model)) julia> optimizer = ADAM(0.001) julia> Flux.train!(loss, params(model), data, optimizer) julia> model = Chain(x -> sqrt(x), x->x-1) 

φ , , , .

Zygote «source-to-source»: , , . differentiable programming — — backpropagation , .

Julia : «source-to-source» , . , .

Julia ?

, — . .

- , , , — .

, , .

Julia , .

• , , . Julia «» .
• , API, , .

Moscow Python Conf++ , 27 , Python Julia. , , telegram- MoscowPython.