نظرية الفئة تسمح للرياضيات بالتخلي عن المساواة

أقنع اثنان من الأعمال الضخمة العديد من علماء الرياضيات بالتخلي عن علامة المساواة. هدفهم هو إعادة بناء أسس الانضباط بمساعدة علاقة أضعف - "التكافؤ". وهذه العملية لا تسير دائمًا بسلاسة.

علامة المساواة هي حجر الزاوية في الرياضيات. يبدو أنه يدلي ببيان أساسي ومتسق: هذان الكيانان متماثلان تمامًا.

ومع ذلك ، فإن دائرة علماء الرياضيات تنمو ، في إشارة إلى علامة المساواة ، مثل الخطأ الأولي للرياضيات. إنهم يعتبرون ذلك بمثابة لمعان خارجي ، يخفي التعقيدات المهمة للعلاقة بين الكميات - التعقيدات التي يمكن أن تفتح الحلول لعدد كبير من المشاكل. إنهم يريدون إصلاح الرياضيات باستخدام لغة تكافؤ أكثر مرونة.

وقال جوناثان كامبل من جامعة ديوك: "لقد ولدنا فكرة المساواة". "وكان ينبغي أن يكون هناك تكافؤ في مكانه."

أبرز شخصية في هذا المجتمع هي جاكوب لوري . في يوليو ، استقال لوري ، البالغ من العمر 41 عامًا ، كموظف متفرغ في جامعة هارفارد لشغل منصب هيئة تدريس في معهد برينستون للدراسات المتقدمة ، حيث عمل بعض أبرز علماء الرياضيات في العالم.

نادراً ما توجد أفكار بمقياس مثل Lurie في أي مجال. في كتبه الممتدة على آلاف الصفحات المليئة بالتفاصيل التقنية ، ابتكر طريقة مختلفة بشكل مدهش عن الطريقة المعتادة لفهم أبسط مفاهيم الرياضيات ، متجاوزًا العلامة المتساوية. وقال مايكل هوبكنز ، عالم الرياضيات بجامعة هارفارد ورئيس كلية الدراسات العليا: "أعتقد أنه بدا له أن هذه هي الطريقة الصحيحة للتفكير في الرياضيات".

نشر كتابه الأول ، The Theory of Topos Topos ، في عام 2009. مجلد من 944 صفحة بمثابة تعليمة لتفسير مجالات الرياضيات المعترف بها في لغة جديدة من "فئات اللانهاية". في السنوات اللاحقة ، اخترقت أفكار لوري مجموعة واسعة من التخصصات الرياضية. العديد من علماء الرياضيات يعتبرونها لا غنى عنها لمستقبل هذا المجال. قال جون فرانسيس من جامعة نورث وسترن: "لن يكون أحد على حاله بعد دراسة فئات اللانهاية".


يعقوب لوري

ومع ذلك ، فإن انتشار فئات اللانهاية كشف جميع المشكلات التي يمر بها مجال محترم من الرياضيات ، في محاولة لاستيعاب الأفكار الجريئة الجديدة - وخاصة فكرة تتحدى أهم مفاهيمها. وقال كلارك بارويك من جامعة إدنبرة: "هناك مستوى معين من النزعة المحافظة في المجتمع الرياضي". "لا أعتقد أنه يمكن توقع أي مجموعة من علماء الرياضيات بسرعة قبول أي أداة دون أسباب مقنعة."

على الرغم من أن العديد من علماء الرياضيات قبلوا فئات اللانهاية ، فإن القليل منهم قرأوا النصوص الكاملة والمجردة للغاية للوري. ونتيجة لذلك ، فإن جزءًا من العمل المستند إلى أفكاره قد أصبح أقل صرامة مما هو مقبول في الرياضيات.

قالت إينا زاخاريفيتش ، عالمة رياضيات في جامعة كورنيل: "سمعت أن الناس يقولون:" لوري لديها مكان ما ". - وأنا أقول: حقا؟ يمكنك الرجوع إلى 8000 صفحة من النص. هذا ليس مرجعًا ، إنه نداء للسلطة ".

لا يزال علماء الرياضيات يحاولون إدراك مدى اتساع أفكار لوري والطريقة الفريدة لتقديمها. إنهم يستخلصون جوهر عرضه لفئات اللانهاية ويقدمونها في حزمة جديدة حتى يتمكن المزيد من علماء الرياضيات من استخدامها. إنهم ، إلى حد ما ، ينفذون القيادة اللازمة ، التي تُلزم باتباع أي ثورة ، وترجمة النص الثوري إلى مدونة القوانين اليومية. وهكذا ، فإنهم يخلقون مستقبل علماء الرياضيات ، ليس على أساس المساواة ، ولكن على أساس التكافؤ.

أبراج التكافؤ لا نهاية لها

يبدو أن المساواة الرياضية هي الأقل إثارة للجدل في جميع الأفكار. حبات اثنين بالإضافة إلى حبة واحدة يساوي ثلاثة حبات. ماذا هناك للحديث عنه؟ ومع ذلك ، يمكن أن تكون أبسط الأفكار الأكثر خادعة.

منذ نهاية القرن التاسع عشر ، تم بناء أسس الرياضيات على مجموعات من الأشياء تسمى مجموعات. تحدد نظرية Set القواعد ، أو البديهية ، لإنشاء هذه المجموعات والتعامل معها. تدعي إحدى هذه البديهيات ، على سبيل المثال ، أنه يمكنك إضافة مجموعة من عنصر واحد إلى مجموعة مكونة من عنصرين والحصول على مجموعة جديدة من ثلاثة عناصر: 2 + 1 = 3.

الطريقة الرسمية لإثبات تكافؤ كميتين هي مطابقة الأزواج مع بعضها البعض. تطابق حبة واحدة إلى يمين علامة المساواة مع حبة واحدة إلى اليسار. بعد كل المقارنات ، لن يكون هناك حبات إضافية متبقية.

تدرك نظرية Set أن مجموعتين من ثلاثة كائنات يمكن أن تتوافق كل منهما بدقة مع بعضها البعض ، ولكن هذا لا يعني جميع الطرق المختلفة الممكنة لمثل هذه المقارنة. يمكن للخرز الأول على اليمين التقاط زوج على شكل أول حبة على اليسار ، أو مطابقة الأول على اليمين والثاني على اليسار ، وما إلى ذلك (يمكن أن يكون هناك ستة أزواج من هذا القبيل). أن نقول أن اثنين زائد واحد يساوي ثلاثة ، ونهاية على هذا يعني عدم رؤية كل الطرق الممكنة لمساواتهم. يقول كامبل: "المشكلة هي أن هناك العديد من الطرق للاقتران". "وننسى لهم عندما نقول يساوي".



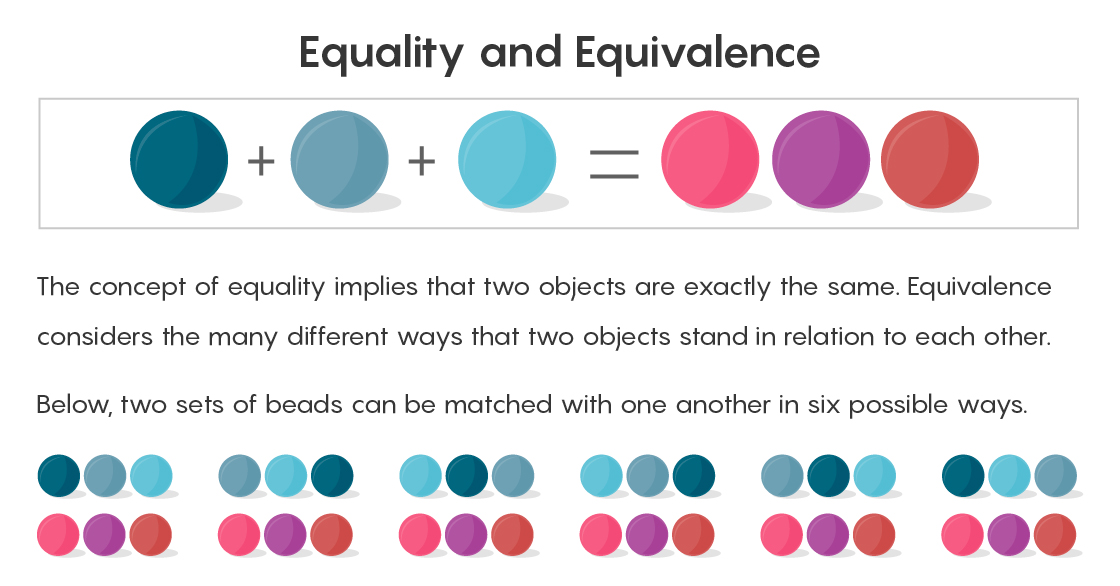
هنا يأتي دور التكافؤ. إذا كانت المساواة علاقة واضحة - شيئان إما متساويان أم لا - يمكن أن يكون التكافؤ مختلفًا.

عندما تتطابق بدقة مع كل عنصر من عناصر مجموعة واحدة لكل عنصر من عناصر أخرى ، فإنك تحصل على معادلة قوية. ولكن ، على سبيل المثال ، في مجال الرياضيات مثل homotopy ، يكون شكلان (أو أشكال هندسية) مكافئين إذا كان يمكن تحويل أحدهما إلى آخر عن طريق التمدد أو الضغط دون كسر.

من وجهة نظر نظرية homotopy ، فإن القرص المسطح ونقطة في الفضاء تعادلان - يمكن ضغط القرص إلى نقطة. ومع ذلك ، لا يمكنك مطابقة النقاط الموجودة على القرص بالنقاط الموجودة على نقطة. في الواقع ، يحتوي قرص النقاط على عدد لا حصر له ، والنقطة هي مجرد نقطة واحدة.



منذ منتصف القرن العشرين ، يحاول علماء الرياضيات تطوير بديل لنظرية نظرية تكون فيها الرياضيات أسهل في التعامل معها من حيث التكافؤ. في عام 1945 ، قدم عالم الرياضيات صموئيل إلبرغ وسوندرز ماكلين كائنًا أساسيًا جديدًا مع تكافؤ مدمج. أطلقوا عليه فئة.

يمكن ملء فئة مع أي شيء. يمكنك أن تأخذ فئة من الثدييات ، والتي سوف تشمل جميع المخلوقات ذات الشعر الدافئ التي تنتج الحليب. أو يمكنك إنشاء فئات من الكائنات الرياضية: مجموعات أو أشكال هندسية أو أنظمة رقمية.

الفئة هي مجموعة تحتوي على بيانات وصفية إضافية: وصف لجميع طرق مطابقة كائن مع آخر ، والذي يتضمن وصفًا لكل الميزات التي يمكن اعتبار كائنين مكافئين بها. يمكن أيضًا تصور الفئات ككائنات هندسية يمثل فيها كل عنصر من عناصر الفئة نقطة.

تخيل ، على سبيل المثال ، سطح الكرة. يمكن أن تشير كل نقطة على هذا السطح إلى نوع المثلثات. تعبر المسارات بين النقاط عن علاقة تكافؤ بين الكائنات. من وجهة نظر نظرية الفئة ، ننسى الطريقة المحددة لوصف كائن والتركيز بدلاً من ذلك على المكان الذي يشغله الكائن بالنسبة لجميع الكائنات الأخرى من هذا النوع.


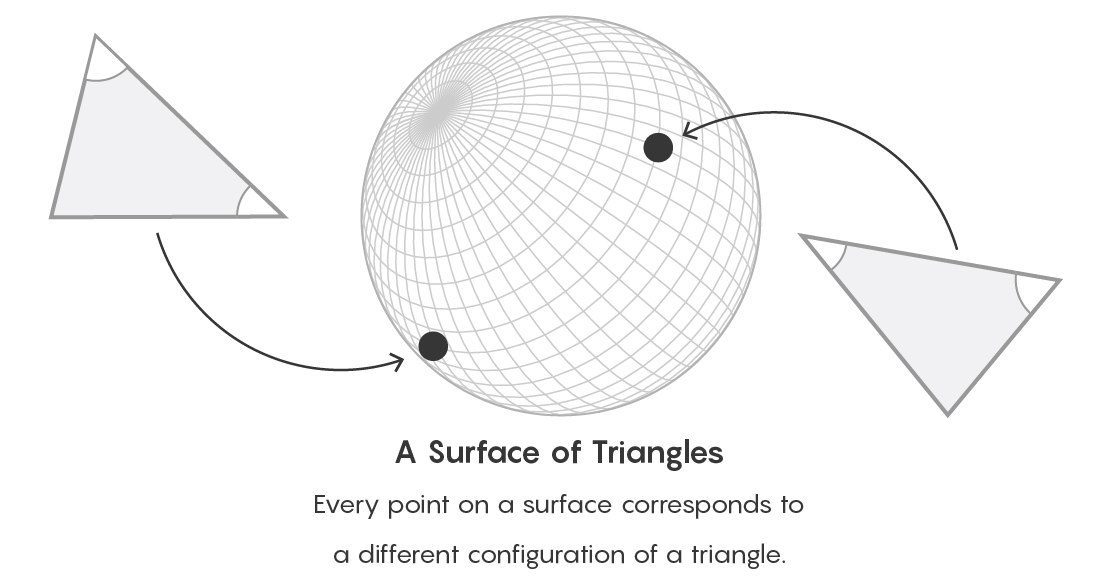كل نقطة على السطح يتوافق مع نوع معين من المثلثات.

قال زاخاريفيتش: "نعامل أشياء كثيرة كأشياء ، رغم أنها في الواقع علاقة بين الأشياء". - تعني عبارة "زوجي" شيئًا نعتبره كائنًا ، لكن يمكنك التفكير فيه كعلاقة. يتم تحديد جزء معين منه من خلال العلاقة معي ".

كان إصدار الفئة من Eilenberg و MacLane مناسبًا تمامًا للعمل مع خيارات تكافؤ قوية. ولكن في النصف الثاني من القرن العشرين ، استخدم علماء الرياضيات بشكل متزايد أشكالًا أضعف من التكافؤ ، مثل homotopy. وقالت إميلي رييل ، عالمة رياضيات بجامعة جونز هوبكنز: "أصبحت الرياضيات أكثر ذكاء ، ولدينا حتما رغبة في أفكار أكثر دقة حول الأشياء العادية". في هذه الإصدارات الدقيقة من التكافؤ ، يزداد مقدار المعلومات حول العلاقة بين كائنين زيادة حادة. لم تكن الفئات البدائية من Eilenberg و MacLane مخصصة لهذا الغرض.

لرؤية زيادة في كمية المعلومات ، تذكر أولاً مجالنا ، مع الإشارة إلى مثلثات مختلفة. يتشابه المثلثان في المثلية إذا كان يمكن تحويل أحدهما إلى آخر عن طريق التمدد أو التشوه الآخر. هناك نقطتان على سطح متساويان بشكل متماثل إذا كان هناك مسار يربطهما. من خلال دراسة المسارات المتجانسة بين النقاط على السطح ، فأنت تدرس بالفعل الطرق المختلفة التي ترتبط بها المثلثات التي تشير إليها هذه النقاط مع بعضها البعض.



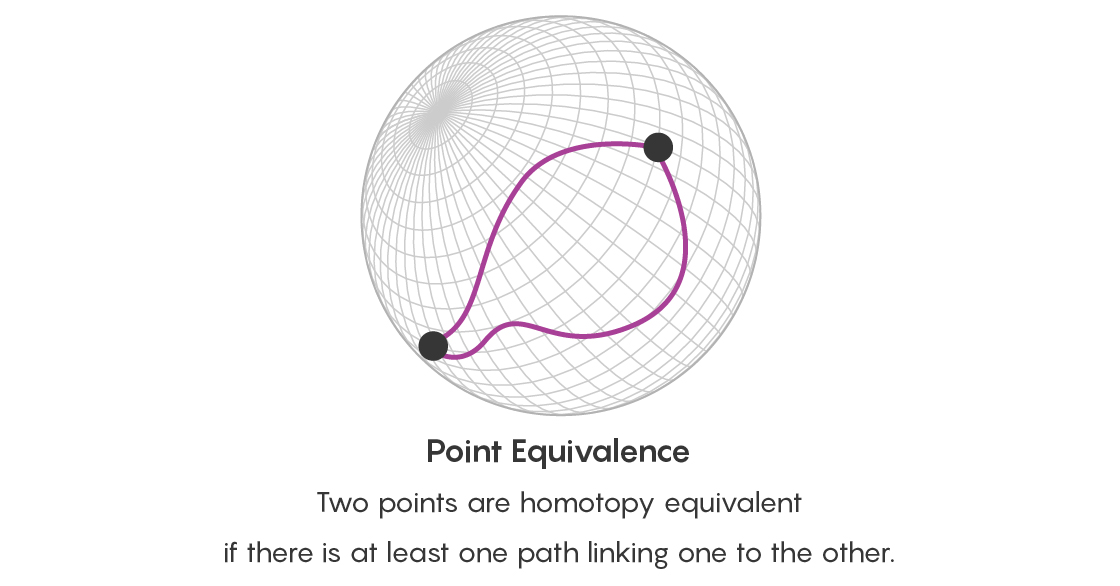
ومع ذلك ، لا يكفي أن نذكر أن هناك نقطتين متصلتين بعدة طرق متكافئة. من الضروري أيضًا التفكير في معادلة كل هذه المسارات. لذلك ، بالإضافة إلى مسألة معادلة النقاط ، أنت الآن تطرح مسألة معادلة مسارين تبدأ وتنتهي في نفس النقاط - وهناك مسار يربط هذه المسارات. يأخذ هذا المسار الذي يربط بين المسارات شكل قرص ، وحدوده من هذين المسارين.



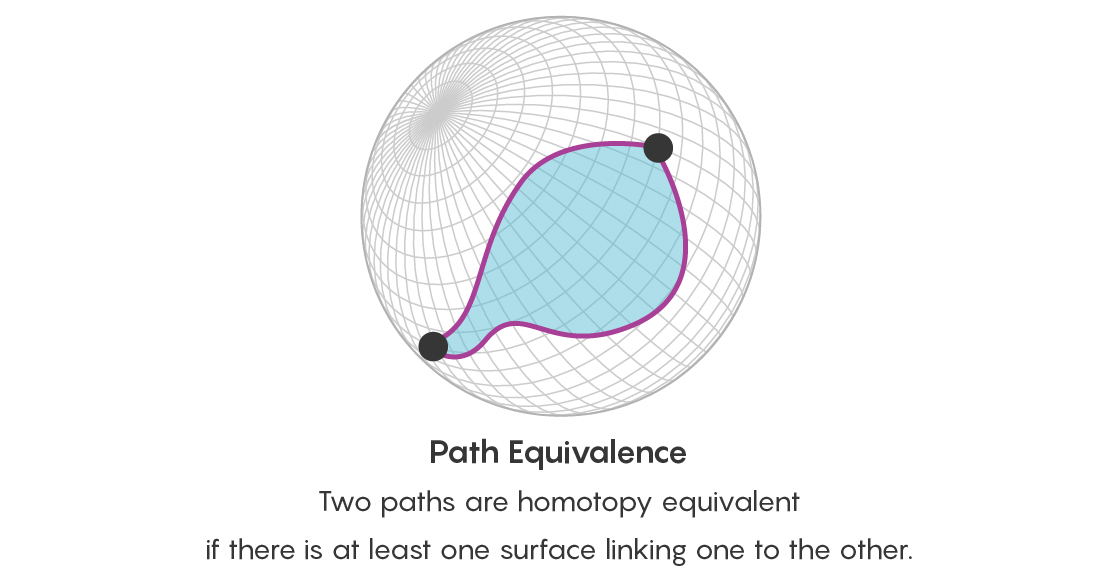
يمكنك تطوير هذه الفكرة بشكل أكبر. يكون القرصان متكافئين إذا كانا متصلين بمسار - وسيأخذ هذا المسار شكل كائن ثلاثي الأبعاد. يمكن توصيل هذه الكائنات ثلاثية الأبعاد نفسها بمسارات ثلاثية الأبعاد (المسار بين كائنين دائمًا له بُعد واحد أكثر من الكائنات نفسها).

نتيجة لذلك ، يمكنك إنشاء برج لا نهاية له من التكافؤ بين المعادلات. إذا جادلنا حول العقيدة بأكملها ، فأنت تقوم بإنشاء عرض عام لجميع الكائنات التي قمت بتمييزها بنقاط على الكرة.

وقال ديفيد بن تسفي من جامعة تكساس في أوستن: "إنها مجرد كرة ، لكن تبين أنه من أجل فهم شكل الكرة ، فأنت بحاجة إلى الذهاب إلى ما لا نهاية".

في العقود الأخيرة من القرن العشرين ، عمل العديد من علماء الرياضيات على نظرية "فئات اللانهاية" - على ما هو قادر على تتبع برج لا حصر له من المعادلات بين المعادلات. حقق بعضهم نجاحًا كبيرًا. لكن وصل واحد فقط إلى النهاية.

إعادة كتابة الرياضيات

أول عمل لجاكوب لوري في فئات اللانهاية لم يكن ناجحًا للغاية. في 5 يونيو 2003 ، نشر العالم البالغ من العمر 25 عامًا وثيقة من 60 صفحة بعنوان " على توبوس إنفينيتي " على موقع المؤلفات العلمية arxiv.org. هناك بدأ في وضع مسودات تقريبية للقواعد التي يمكن من خلالها لعلماء الرياضيات العمل مع فئات اللانهاية.

لم يقبل الجميع العمل الأول بنفس الطريقة. بعد فترة وجيزة من القراءة ، كتب بيتر ماي ، عالم الرياضيات في جامعة شيكاغو ، لمشرف لوري ، مايكل هوبكنز ، أنه على الرغم من أن عمل لوري يحتوي على أفكار مثيرة للاهتمام ، إلا أنه يبدو غير مكتمل ويتطلب نهجًا أكثر انضباطًا.

"لقد أوضحت تعليقاتنا لمايك ، ونقلها إلى يعقوب" ، قال ماي.

يبقى مجهولًا ما إذا كان لوري قد أخذ خطاب مايو كتحدي ، أو إذا كان قد خطط بالفعل لخطوته التالية (رفض لوري طلبات عديدة لإجراء مقابلة). من الواضح أنه بعد تلقي التعليقات الهامة ، وصل لوري إلى فترة إنتاجية متعددة السنوات ، والتي أصبحت فيما بعد أسطورية.

قال ماي: "لا يمكنني الدخول في دماغ يعقوب ، وبالتالي لا أعرف بالضبط ما كان يفكر فيه". "ولكن هناك فرق كبير بين المسودة التي قمنا بمراجعتها والإصدارات النهائية ، والتي توجد بالفعل على مستوى رياضي مختلف تمامًا."

في عام 2006 ، نشر لوري على arxiv.org مسودة "نظريات أعلى توبوس". في هذا العمل الضخم ، ابتكر الجهاز الضروري لاستبدال نظرية المجموعات بقاعدة جديدة للرياضيات تعتمد على فئات اللانهاية. وقال تشارلز رزق ، عالم الرياضيات بجامعة إلينوي في أوربانا شامبين ، الذي قام بعمل هام في مرحلة مبكرة في تطوير فئات اللانهاية: "لقد أنشأ حرفيًا آلاف الصفحات من هذا الجهاز الأساسي التي نستخدمها جميعًا الآن". "لا أستطيع أن أتخيل كيف يمكن إنشاء عمل مثل" نظرية أعلى Topos "في العمر - وقد صنعه في غضون عامين أو ثلاثة أعوام."

ثم في عام 2011 ، قدم لوري عملًا آخر أطول. في ذلك ، اختراع الجبر.

تعطينا الجبر مجموعة رائعة من القواعد الرسمية لمعالجة المعادلات. يستخدم علماء الرياضيات هذه القواعد باستمرار لإثبات النظريات. ومع ذلك ، لا الجبر الجمباز على أشرطة ثابتة من علامة المساواة. قم بإزالة هذه الأعمدة واستبدالها بمفهوم التكافؤ المؤقت ، وستصبح بعض العمليات معقدة للغاية.

تأخذ واحدة من القواعد الأولى للجبر التي يتعلمها الأطفال في المدرسة: associativity. لا يعتمد مجموع أو منتج ثلاثة أرقام أو أكثر على تجميعهم: 2 × (3 × 4) = (2 × 3) × 4.

من السهل إثبات خاصية associativity لقائمة من ثلاثة أرقام أو أكثر إذا كنت تعمل على قدم المساواة. هذا أمر صعب عند العمل حتى مع مفهوم التكافؤ القوي. ولكن عندما تنتقل إلى إصدارات أكثر دقة من التكافؤ ، مع أبراج مسارات لا حصر لها من الطرق التي تربط بين المسارات ، حتى قاعدة بسيطة ، على غرار associativity ، تتحول إلى غابة مظلمة.


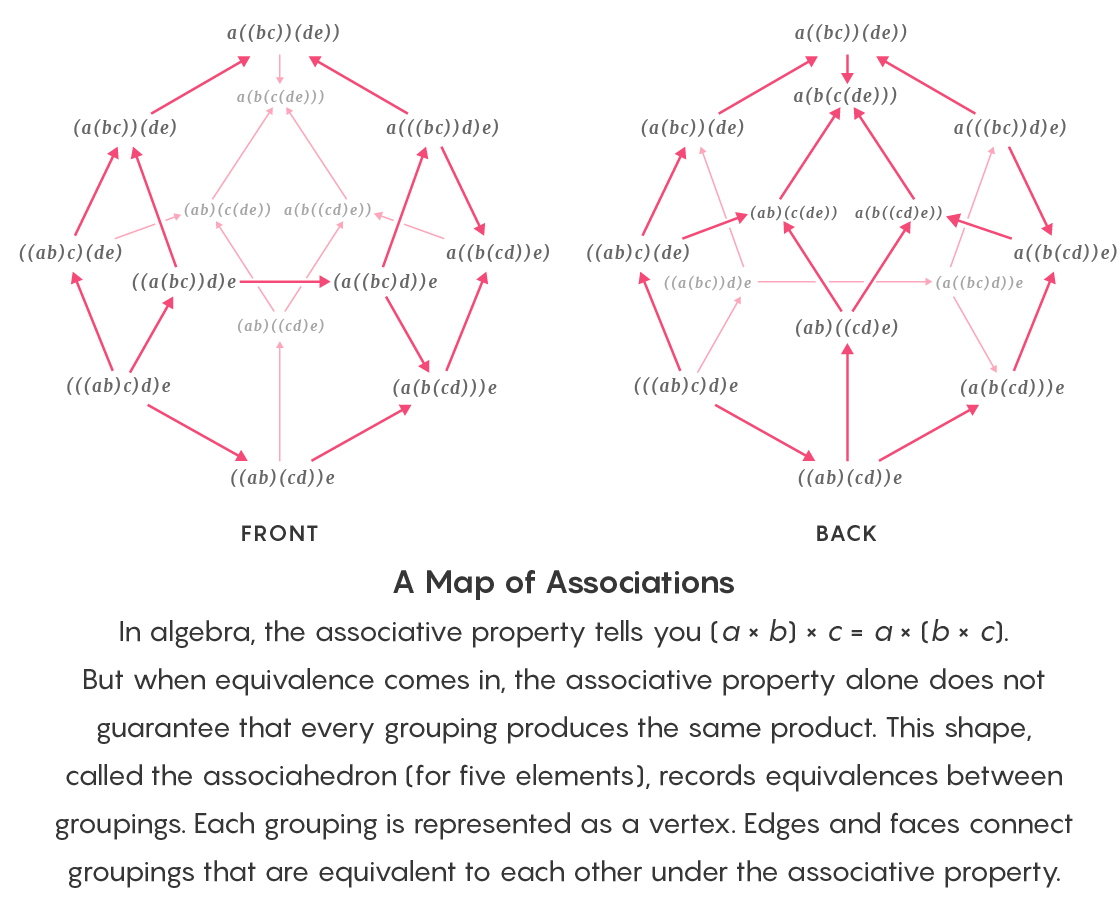في الجبر ، تنص associativity على أن (أ × ب) × ج = أ × (ب × ج). ولكن مع استخدام التكافؤ ، فإن الارتباطية وحدها لا تضمن أن أي مجموعة من العناصر سوف تسفر عن نفس نتيجة الضرب. يحتوي هذا assocahedron على سجلات معادلة المجموعة. كل قمة تتوافق مع مجموعة. تجمع الحواف والوجوه بين المجموعات التي تعادل بعضها بعضًا.

وقال ديفيد إيسلا ، عالم الرياضيات في جامعة مونتانا: "هذا يجعل المشكلة معقدة للغاية ، مما يجعل من المستحيل العمل مع هذه النسخة الجديدة من الرياضيات".

في الجبر العالي ، الذي امتد الإصدار الأخير منه إلى أكثر من 1553 صفحة ، طوّر لوري خيار الارتباط لفئات اللانهاية - بالإضافة إلى العديد من نظريات الجبر الأخرى التي تشكل معًا أساس الرياضيات المعادلات.

أنتج هذان الكتابان تأثير القنبلة المتفجرة. مثل هذه الأعمال تؤدي إلى ثورة علمية. "الحجم كان استثنائي ،" قال ريل. "لقد كان تحقيق مستوى Grothendieck في الهندسة الجبرية."

ومع ذلك ، فإن الثورة تستغرق وقتًا ، وكما اكتشف علماء الرياضيات بعد نشر كتب لوري ، فقد تكون هذه السنوات فوضوية.

هضم بقرة

يُعتبر علماء الرياضيات أشخاصًا ذوي تفكير لا لبس فيه: البرهان إما صحيح أم لا ؛ الفكرة إما تعمل أم لا. ومع ذلك ، فإن علماء الرياضيات هم أيضًا أناس عاديون ، ويتفاعلون مع الأفكار الجديدة بنفس الطريقة التي يتبعها الأشخاص العاديون: ذاتيًا ، وعاطفيًا ، لديهم دوافع شخصية.

وقال كامبل "أعتقد أن الكثير من النصوص قد كتبت عن علماء الرياضيات بنبرة تجعلهم يبحثون عن حقيقة واضحة وضوح الشمس". "لكن هذا لا يحدث". هؤلاء أشخاص لهم أذواقهم ومناطق الراحة الخاصة بهم ، ويمكنهم حرمان الأشياء التي لا يحبونها لأسباب جمالية أو شخصية. "

في هذا الصدد ، أصبح عمل لوري تحديا معقدا للمجتمع. في الحقيقة ، لقد كانت استفزازية: إليك طريقة جديدة وأفضل للقيام بالرياضيات. تم توجيه هذه الرسالة بشكل خاص إلى علماء الرياضيات ، الذين قضوا حياتهم المهنية بأكملها في تطوير الأساليب التي تفوق لوري.

وقال فرانسيس: "لا يرغب الناس دائمًا في رؤية الجيل القادم يعيد كتابة أعمالهم ، وهذه العملية تخلق التوتر". "هذه هي واحدة من ملامح نظرية فئات اللانهاية - معظم الأعمال السابقة تتوافق."

كان من الصعب هضم عمل لوري لأسباب أخرى. يعني حجم المواد أن على علماء الرياضيات قضاء سنوات في قراءة كتبه. يكاد يكون من المستحيل أن تطلب من علماء الرياضيات المشغولين الذين هم في منتصف حياتهم المهنية ، وبالنسبة لطلاب الدراسات العليا الذين لديهم بضع سنوات فقط لإعطاء نتيجة تتيح لهم العثور على وظيفة ، وهذا أمر محفوف بالمخاطر للغاية.

كان عمل لوري مجرداً للغاية ، حتى بالمقارنة مع الطبيعة المجردة للغاية لكل شيء في دراسات الرياضيات المتقدمة. وليس الجميع يحب ذلك. وقالت كامبل: "اعتقد الكثير من الناس أن عمل لوري كان مجرد هراء مجردة ، والكثير منهم وقعوا في حبها". "كانت هناك خيارات وسيطة ، بما في ذلك أولئك الذين لم يفهموها على الإطلاق."


إميلي بكرة

المجتمع العلمي يقبل باستمرار الأفكار الجديدة ، ولكن عادة ما يحدث هذا ببطء والشعور بأن الجميع يتحرك في نفس الوقت. ظهور أفكار جديدة يخلق صعوبات للجهاز الفكري للمجتمع. وقال كامبل "هناك الكثير من الأشياء الجديدة التي تطرأ على الفور - إنها مثل بوا تحاول هضم بقرة". "كتلة ضخمة تمر عبر المجتمع."

إذا كنت عالم رياضيات تعتقد أن نهج لوري هو أفضل طريقة لممارسة الرياضيات ، فسيكون طريقك إلى الأمام وحيدًا. قلة من الناس يقرؤون أعمال لوري ، لم تكن هناك كتب مدرسية لإعادة سردها لفترة وجيزة ، ولا توجد ندوات لمساعدتك في الحصول على دروسك. وقال بيتر هاين ، وهو طالب دراسات عليا في معهد ماساتشوستس للتكنولوجيا قضى عاماً في قراءة أعمال لوري: "كانت هناك طريقة واحدة فقط لدراسة كل هذا بتفصيل كبير - الجلوس والقيام بكل شيء بنفسك". - أعتقد أن هذا هو الأكثر صعوبة. "ليس من السهل أن تجلس وتكتشف كل شيء بنفسك - أي الجلوس وقراءة 800 صفحة من Theory of the Topos Theory بنفسك."

مثل العديد من الاختراعات الجديدة ، تتطلب نظرية أعلى topos علماء الرياضيات للتفاعل بنشاط مع الجهاز ، والذي يسمح لها بالعمل.هذه هي الطريقة التي تجعل كل صبي يبلغ من العمر 16 عامًا يحلم برخصة قيادة يتعلم أولاً كيفية فرز المحرك. وقال دينيس جيتسجوري ، عالم الرياضيات بجامعة هارفارد الذي عمل مع لوري: "إذا كانت هناك نسخة أكثر ودا من كل هذا ، فإن النظرية ستصبح على الفور أكثر سهولة للدوائر الرياضية الأوسع".

عندما بدأ الناس في قراءة أعمال لوري واستخدام فئات اللانهاية في دراساتهم ، ظهرت مشاكل أخرى. بنى علماء الرياضيات أعمالهم على أساس فئات اللانهاية. تلقى مراجعو المجلات هذه الأوراق وسألوا: ما هذا؟

وقال بارفيك: "كان هناك موقف عاد فيه العمل إما من المجلات بمراجعات سخيفة ، والتي كان الافتقار التام لفهمها واضحًا ، أو استغرق الأمر عدة سنوات لنشرها". "قد يكون هذا كثيرًا من الإزعاج ، لأن العمل غير المنشور الذي تم على موقعك لسنوات يبدو أكثر سخافة."

ومع ذلك ، فإن المشكلة الأكبر لم تكن الأعمال غير المنشورة ، ولكنها تعمل باستخدام فئات اللانهاية ، والمنشورة - ولكن تحتوي على أخطاء.

كتب لوري هي المصدر الوحيد الموثوق للمعلومات حول فئات اللانهاية. إنها صارمة ، لكن من الصعب فهمها تمامًا. كما أنها غير مناسبة بشكل خاص لدور الإرشادات التي يمكن الرجوع إليها - من الصعب البحث عن نظريات معينة ، أو التحقق من أن تطبيقًا معينًا لفئات اللانهاية المصادفة في عمل شخص ما يعمل حقًا.

وقال أندريه جويال: "معظم علماء الرياضيات العاملين في هذا المجال لم يقرؤوا لوري بشكل منهجي"، عالم رياضيات من جامعة كيبيك في مونتريال ، وكان عمله المبكر عنصرا أساسيا في كتب لوري. "يستغرق الأمر الكثير من الوقت والجهد ، لذلك نحن نفترض فقط أن كل ما هو مكتوب في كتبه صحيح - لأنه في كل مرة نتفحص فيها شيئًا ما ، يتضح أنه صحيح. في الواقع ، في كل مرة. "

أدى عدم إمكانية الوصول إلى كتب لوري إلى عدم الدقة في بعض الدراسات التي تلت ذلك. من الصعب قراءة كتب لوري ، ومن الصعب اقتباسها ، ومن الصعب استخدامها لاختبار عمل الآخرين.

"إن الأدب العام حول موضوع فئات اللانهاية يبدو فوضوي" ، قال Zakharevich.

على الرغم من كل شكلياتها ، لا ينبغي أن تكون الرياضيات نصًا مقدسًا لا يستطيع إلا الكهنة قراءته. في هذا المجال ، لا يتطلب الأمر مجلدات سميكة فحسب ، بل أيضًا كتيبات ، وليس فقط الكشف الأولي ، ولكن أيضًا تفسيرات أوصافها. في غضون ذلك ، توجد نظرية فئات اللانهاية ، في معظمها ، في شكل العديد من الكتب الكبيرة على الرف.

قال رزق: "يمكنك اتباع النهج." سوف يعطيك يعقوب ما يجب القيام به ، وكل شيء على ما يرام ". "أو يمكنك أن تقرر" لا نعرف كيفية تقديم موضوعنا جيدًا بما فيه الكفاية حتى يتمكن الناس من استخدامه. "

ومع ذلك ، كان عدد قليل من علماء الرياضيات قادرين على قبول التحدي وجعل فئة اللانهاية تقنية يمكن أن يستخدمها عدد أكبر من الأشخاص من مجال دراستهم.

نظرية المستخدم ودية

لترجمة فئات اللانهائي إلى كائن قادر على العمل الرياضي الحقيقي ، كان على لوري أن يثبت النظريات المرتبطة بها. ولهذا ، كان عليه أن يختار منظرًا طبيعيًا لإنشاء هذا الدليل - مثله مثل أي شخص يشارك في الهندسة ، من الضروري اختيار نظام تنسيق للعمل. علماء الرياضيات نسمي هذا الاختيار النموذجي.

طورت لوري فئات اللانهائية على نموذج الفئات شبه. طور علماء الرياضيات الآخرون من قبله فئات اللانهائية على نماذج أخرى. وعلى الرغم من أن عملهم لم يكن شاملاً مثل عمل لوري ، إلا أنه في بعض الحالات يكون التعامل معهم أسهل. قال زاخاريفيتش: "لقد اختار يعقوب نموذجًا وتحقق من أن كل شيء يعمل فيه ، لكنه غالبًا ما يكون ليس الأسهل".

في الهندسة ، يفهم علماء الرياضيات بوضوح كيفية التنقل بين أنظمة الإحداثيات المختلفة. لقد أثبتوا أيضًا أن النظريات أثبتت في بعض الظروف أنها تعمل في حالات أخرى.

بالنسبة لفئات اللانهاية ، هذه الضمانات غير موجودة. ومع ذلك ، عندما يكتب علماء الرياضيات أعمالهم باستخدام فئات اللانهائي ، فإنهم غالبًا ما يسهلون التبديل بين النماذج ، مما يشير (ولكن لا يثبت) قابلية نقل النتائج. وقال هاين "الناس لا يحددون ما يفعلونه ، إنهم يتنقلون بين كل هذه النماذج المختلفة ، ويقولون: آه ، هذا هو الشيء نفسه". "لكن هذا ليس دليلا."

على مدار السنوات الست الماضية ، حاول اثنان من علماء الرياضيات الحصول على هذه الضمانات. ريل ودومينيك حقيقةمن جامعة McUyra في أستراليا ، وضعت طريقة لوصف فئات اللانهاية ، والتغلب على الصعوبات التي ظهرت في المنصات السابقة باستخدام نماذج معينة. أثبت عملهم ، استنادًا إلى أعمال بارفيك السابقة وغيرها ، أن العديد من نظريات نظرية توبوس العليا تظل صحيحة بغض النظر عن النموذج المستخدم. وقد أثبتوا هذا التوافق بطريقة مناسبة: "نحن ندرس فئات اللانهاية ، والتي تكون كائناتها هي فئات اللانهاية" ، قال Ril. "نظرية الفئة تعض ذيلها."

يأمل Ril and Verity في تطوير نظرية فئات اللانهاية بطريقة أخرى. اختاروا جوانب النظرية التي تعمل بغض النظر عن النموذج. يتمتع هذا العرض التقديمي ، بغض النظر عن النموذج ، بنوعية ملائمة من قابلية التطبيق الفوري ، والتي يأملون أن تجتذب علماء الرياضيات إلى هذا المجال من البحث الذين ابتعدوا عنه عندما كانت المدخلة الوحيدة هي The Higher Topos Theory.

وقال هوبكنز: "للدخول إلى هذا العالم ، تحتاج إلى التغلب على الخندق المائي". "ويفعلون ذلك خفض الجسر."

خطة Ryl و Verity لإنهاء العمل في العام المقبل. وفي الوقت نفسه ، بدأت لوري مؤخرا العمل في مشروع Kerodon.، الذي خطط لتحويله إلى نوع من الكتب المرجعية حول نظرية الفئة العليا ، على غرار ويكيبيديا. بعد مضي ثلاثة عشر عامًا على إضفاء الطابع الرسمي على نظرية التوبوس في رياضيات التكافؤ ، تحاول هذه المبادرات تنقيح ونشر هذه الأفكار - من أجل جعل رياضيات التكافؤ أكثر سهولة.

"إن العبقرية تلعب دورًا مهمًا في تطوير الرياضيات ، لكن المعرفة بحد ذاتها هي نتيجة عمل المجتمع بأكمله" ، قال تشويال. "إن الهدف الحقيقي للمعرفة هو أن تصبح معرفة المجتمع بأسره ، وليس الانتماء إلى شخص أو اثنين."