على خطى
"ربحنا: TopCoder Open 2019" قمت بنشر المهام من مسار الخوارزمية
(البرمجة الرياضية الكلاسيكية. في غضون ساعة ونصف ، تحتاج إلى حل ثلاث مشاكل في Java أو C # أو C ++ أو Python.)1. فطيرة لمدة ستة
بيان المشكلةالمهلة هي 4 ثوان.
لديك فطيرة. من الأعلى ، تكون الكعكة على شكل مضلع محدب (صارم). يتم إعطاء إحداثيات القمم في الأعداد الصحيحة X و Y.
لديك خمسة اصدقاء. تريد تقسيم الكعكة إلى ست قطع من مساحة متساوية (ولكن ليس بالضرورة نفس الشكل). بالطبع ، يمكن لأي شخص القيام بذلك في خمس تخفيضات ، ولكن فقط الايجابيات يمكنهم القيام بذلك في ثلاث تخفيضات.
ابحث عن ثلاث قطع في خطوط مستقيمة من خلال نقطة واحدة تقسم الكعكة إلى ست قطع متساوية الحجم. اطبع {x، y، d1، d2، d3}، حيث (x، y) هي النقطة المشتركة لجميع الأقسام الثلاثة، و d1، d2، d3 هي زوايا اتجاه المقاطع بالراديان.
تعريفالفئة: CakeForSix
الطريقة: قطع
المعلمات: int [] ، int []
العوائد: ضعف []
توقيع الطريقة: ضعف [] قطع (int [] س ، كثافة العمليات [] ذ)
(تأكد من أن طريقتك عامة)
الملاحظات- الاتجاه الإيجابي على طول المحور س هو 0 (راديان) ، والاتجاه الإيجابي على طول المحور ص هو pi / 2 (راديان).
- يشبه القص في الاتجاه d القطع في الاتجاه pi * k + d لأي عدد صحيح k.
- يمكنك إخراج أي اتجاهات ، ليس من الضروري أن تكون من [0 ، pi).
- سوف يقوم الممهِّل بحساب مساحة قطع الكعكة الستة في الزوجي. سيتم قبول الإجابة إذا كان الفرق النسبي أو المطلق بينهما أقل من 10 ^ (- 4).
- بتعبير أدق ، اجعل X و Y أصغر وأكبر المناطق الستة التي تم حسابها بواسطة الممهدة. ثم سيتم قبول إجابتك إذا كانت Y <max (X + 10 ^ (- 4) ، X * 1 + 10 ^ (- 4))).
- (في الإصدار الأصلي من المشكلة ، تم استخدام الدقة 1e-7 بدلاً من 1e-4. لحل هذه المشكلة في الأرشيف ، تم تخفيض حد الدقة بسبب وجود حالات استدعاء تجعل المهمة على الأرجح غير قابلة للحل مع الدقة 1e-7. في عالم مثالي ، القيود لا تسمح بمثل هذه الحالات ولا تزال تتطلب دقة عالية ، لذلك ليس من السهل حل المشكلة باستخدام بعض التحسين الرقمي العام.)
قيود- تحتوي x على 3 إلى 50 عنصرًا شاملاً.
- y يحتوي على العديد من العناصر مثل x.
- جميع الإحداثيات بين 0 و 10000 ضمنا
- يحدد x و y مضلع محدب في اتجاه عقارب الساعة.
الأصل باللغة الإنجليزيةبيان المشكلة
المهلة هي 4 ثوان.
لديك كعكة. من الأعلى ، تعتبر الكعكة مضلع محدب (صارم). يتم إعطاء إحداثيات رؤوسها في int [] sx و y.
لديك خمسة اصدقاء. تريد الآن قطع الكعكة إلى ست قطع من المساحة المتساوية (ولكن ليس بالضرورة شكل متساوٍ). بالطبع ، يمكن لأي شخص القيام بذلك في خمس تخفيضات - ولكن فقط المؤيد الحقيقي يمكنه القيام بذلك في ثلاث عمليات!
العثور على ثلاث قطع خط مستقيم تمر عبر نفس النقطة التي تقطع الكعكة إلى ستة أجزاء كبيرة على قدم المساواة. قم بإرجاع {x، y، d1، d2، d3} ، حيث (x، y) هي النقطة المشتركة بين القطع الثلاثة ، و d1، d2، d3 هي اتجاهاتهم في راديان.
تعريف
الفئة: CakeForSix
الطريقة: قطع
المعلمات: int [] ، int []
العوائد: ضعف []
توقيع الطريقة: ضعف [] قطع (int [] س ، كثافة العمليات [] ذ)
(تأكد من أن طريقتك عامة)
ملاحظات
- الاتجاه الإيجابي على طول المحور س هو 0 (راديان) ، والاتجاه الإيجابي على طول المحور ص هو pi / 2 (راديان).
- القطع في الاتجاه d هو نفسه القطع في الاتجاه pi * k + d لأي عدد صحيح k.
- يمكنك إرجاع أي اتجاهات ، ليس من الضروري أن تكون من [0 ، pi).
- سوف يقوم طلاب الصف بحساب مناطق قطع الكيك الست في الزوجي. سيتم قبول الإجابة إذا كان الفرق النسبي أو المطلق بينهما أقل من 10 ^ (- 4).
- بتعبير أدق ، اجعل X و Y أصغر وأكبر المناطق الستة ، حسب حساب الممهدة. بعد ذلك ، سيتم قبول إجابتك إذا كانت Y <max (X + 10 ^ (- 4) ، X * (1 + 10 ^ (- 4))).
- (النسخة الأصلية من المشكلة استخدمت الدقة 1e-7 بدلاً من 1e-4. .للتغلب على هذه المشكلة في الأرشيف ، تم تخفيض حد الدقة بسبب وجود حالات التحدي التي من المرجح أن تجعل المهمة غير قابلة للحل بدقة 1e-7 في عالم مثالي ، لن تسمح القيود بمثل هذه الحالات ولا تزال تتطلب دقة عالية ، بحيث لا يكون من السهل حل المشكلة عن طريق بعض التحسينات الرقمية العامة.)
القيود
- سيكون x بين 3 و 50 عنصرًا ، شاملاً.
- y سيكون لها نفس عدد العناصر مثل x.
- جميع الإحداثيات ستكون بين 0 و 10000 ، شاملة.
- سيصف x و y مضلع محدب بالترتيب عكس اتجاه عقارب الساعة.
أمثلة
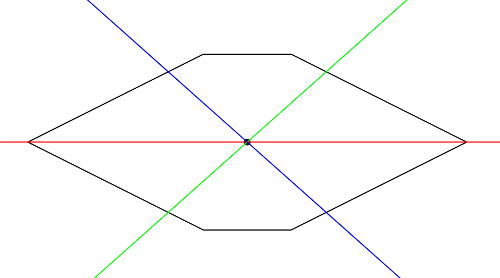
0){0 ، 20 ، 30 ، 50 ، 30 ، 20}
{10 ، 0 ، 0 ، 10 ، 20 ، 20}
العوائد:
{24.999999999437453 ، 9.999999999500002 ، 0.0 ، 0.7266423406817211 ، 2.4149503129080787}
متماثل ولكن ليس مسدس منتظم. مثال على إجابة يتوافق مع تقطيعها إلى النصف أفقيا وجعل اثنين من قطع أخرى في المركز ، والتي تقسم كل جزء إلى ثلاثة أجزاء.
 1)
1){0 ، 1000 ، 0}
{0 ، 0 ، 1000}
العوائد:
{333.3333333331763، 333.3333333332546، 0.7853981633986264، 2.0344439357948154، 2.6779450445891753}
المثلث الأيمن مرة أخرى ، يمكننا أن نبدأ مع واحد من ثلاثة تخفيضات على طول محور التماثل.
 2)
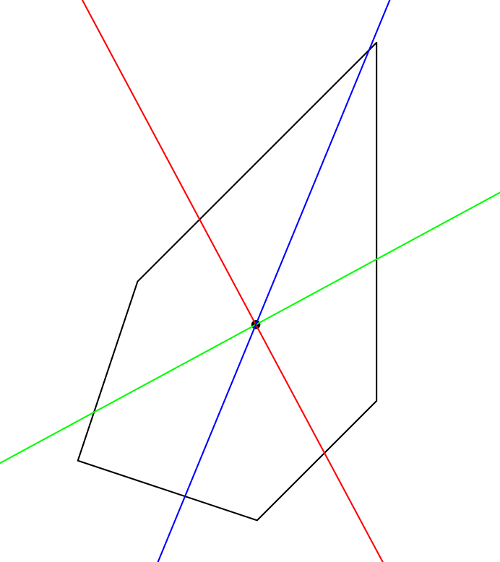
2){40 ، 70 ، 90 ، 90 ، 50}
{30 ، 20 ، 40 ، 100 ، 60}
العوائد:
{69.79517771922892 ، 52.77575974637605 ، 2.0616329654335885 ، 3.637826104091601 ، 4.32123485812475}
البنتاغون الخطأ.
 3)
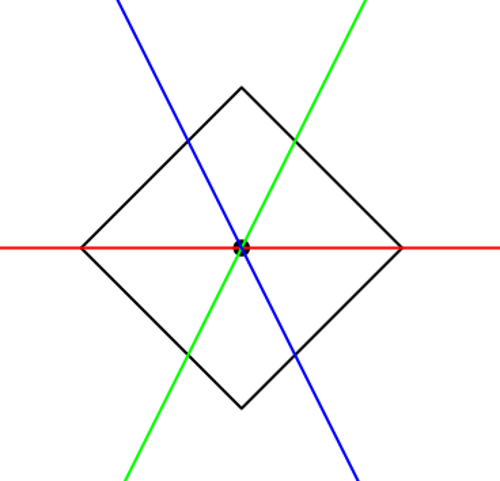
3){300 ، 400 ، 300 ، 200}
{500 ، 600 ، 700 ، 600}
العوائد: {299.99999999974995 ، 599.9999999995 ، 0.0 ، 1.107148717794088 ، 2.034443935795705}
استدارة مربع 45 درجة.
[
المصدر ]