الحصان يتحرك بت. لوح الشطرنج

مساء الخير كتبت هذا المقال خاصةً لطلاب الدورة التدريبية "الخوارزميات للمطورين" في OTUS واليوم أريد مشاركتها مع جميع قراء مدونتنا.

حصان الشطرنج يقف على رقعة الشطرنج وينظر بعناية إلى رقعة الشطرنج.
كم من التحركات المختلفة يمكن أن يفعل؟



الحمد لله مخترع لعبة الشطرنج ، هناك 64 خلية على السبورة.
الثناء على مهندس الكمبيوتر - نوع ulong أيضا 64 بت.
كان هذا صدفة أن يحدث!
الفكرة الرائعة تقترح نفسها - لتخزين اللوحة بأكملها برقم واحد ! هناك حتى مصطلح خاص لهذا الحل - Bitboard - لوحة صغيرة.

إذا كيف يمكنك العثور بسرعة على عدد حركات الشطرنج باستخدام هذه الفكرة؟

المقدمة: knightNr - رقم خلية اللوحة حيث يكون الحصان (من 0 إلى 63).
من الضروري: moveCount - عدد الحقول التي يمكن أن تذهب (من 2 إلى 8).

الخوارزمية.

1. تحويل رقم قفص الحصان إلى ulong - قيمة لوحة البت
الفارس -> الفارس

2. تعيين بت لجميع التحركات الممكنة للحصان
الفارس -> التحركات

3. عد عدد وحدات البتات
التحركات -> التحركات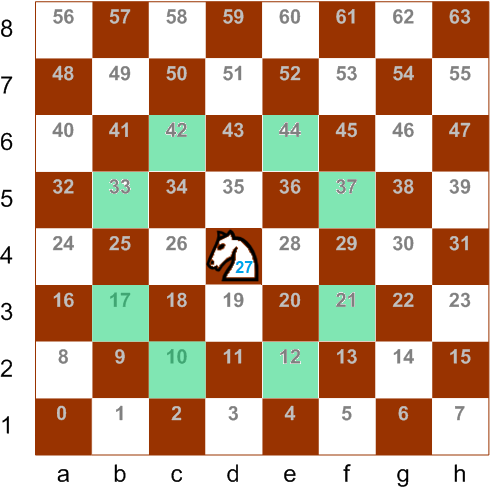



الخطوة الأولى بسيطة للغاية ، تحتاج إلى تحويل صفر بت إلى اليسار من خلال عدد المواضع المحددة.

ulong knightBits = 1 << knightNr; 

والخطوة الثانية هي أكثر تعقيدا قليلا. يمكن أن يذهب الحصان في 8 اتجاهات مختلفة. سننظر في هذه الإزاحات "أفقياً / عمودياً" ، لكن بمواضع البت. وهذا هو ، ونحن نعتبر عدد المواقف التي تحتاجها لتحويل بداية البداية لكل خطوة. ثم "نضيف" كل شيء من خلال عملية "أو" منطقية.

لنبدأ في سرد ​​التحركات من الجانب الأيسر من اللوحة إلى اليمين:

  movesBits = knightBits << 6 | knightBits >> 10 //  b5  b3 | knightBits << 15 | knightBits >> 17 //  c6  c2 | knightBits << 17 | knightBits >> 15 //  e6  e2 | knightBits << 10 | knightBits >> 6 //  f5  f3; 

صحيح ، بارد!

لسوء الحظ ، هناك "ثقوب سوداء" عند حواف اللوحة. على سبيل المثال ، وفقًا لهذه الخوارزمية ، من الخلية a4 (بت # 24) ، يمكنك الوصول إلى الخلية g2 (بت # 14 = 24 - 10) ، هذه القفزة عبارة عن تحريك عن بعد لحصان الشطرنج الكروي في فراغ على لوحة عبر فتحة سوداء حتى العمودي المتطرفة ...

لاستبعاد القفزة الكمية للحصان فوق حافة اللوحة ، من الضروري "فصل" النطاقات الشديدة بعد الحركة. على سبيل المثال ، بالنسبة إلى التحركات +6 و -10 (خليتان إلى اليسار) ، من الضروري إلغاء القيم التي تم الحصول عليها على عمودي g و h ، حيث لا يمكن أن ينتهي بك الأمر في هذه العموديات بعد تحريك "اليسار" لحركتين.

للقيام بذلك ، نحتاج إلى ثوابت الشبكة ذات 4 بتات ، حيث يتم ضبط كل البتات على 1 ، باستثناء العموديات المشار إليها. وهي:

  ulong nA = 0xFeFeFeFeFeFeFeFe; ulong nAB = 0xFcFcFcFcFcFcFcFc; ulong nH = 0x7f7f7f7f7f7f7f7f; ulong nGH = 0x3f3f3f3f3f3f3f3f; 

يوجد في الجزء العلوي والسفلي من رقعة الشطرنج "ثقوب سوداء" تمتص الحصان تمامًا ، لذلك لا يلزم التحقق منها بشكل منفصل.

الآن تبدو الخوارزمية لتوليد تحركات الحصان المسموح بها كما يلي:

  movesBits = nGH & (knightBits << 6 | knightBits >> 10) | nH & (knightBits << 15 | knightBits >> 17) | nA & (knightBits << 17 | knightBits >> 15) | nAB & (knightBits << 10 | knightBits >> 6); 

انها تعمل جدا (!) بسرعة.

بعض القراد - ولدينا صورة نقطية لجميع مغامرات الخيول الممكنة. الأمر المدهش هو أن هذه الخوارزمية تعمل بشكل جيد حتى لو كان هناك العديد من الخيول على السبورة. انه يولد في وقت واحد كل التحركات الممكنة لجميع الخيول! صحيح ، عظيم!

يبقى لحساب عدد البتات

أسهل طريقة هي تحويل الرقم 1 بت إلى اليمين وعدهم. صعوبة - 64 عملية. الذاكرة - 64 بت.

تتمثل أسرع طريقة في إنشاء ذاكرة تخزين مؤقت / صفيف مع 65536 عنصرًا ، حيث تتم كتابة عدد البتات لكل فهرس من 0 إلى 65535. وإضافة 4 عناصر من هذه الصفيف تتوافق مع شرائح 16 بت التالية من الرقم.
صعوبة - 4 عمليات. الذاكرة - 64 كيلو بايت.

لكننا سننظر في الطريقة الأكثر صعوبة ، حيث أن درجة تعقيدها تساوي عدد البتات الفردية في العدد. نظرًا لعدم وجود العديد من التحركات ، سيكون هذا النهج هو الأفضل بالنسبة لنا.

بادئ ذي بدء ، نلاحظ أنه من خلال طرح وحدة من رقم ، فإننا نحول كل الأصفار "الصحيحة" إلى وحدات ، والوحدة الخارجية إلى صفر:

 1001010100010000 - 1 = 1001010100001111 

بعد ذلك ، قم بتطبيق العملية المنطقية "و" لهذه الأرقام:

 1001010100010000 & 1001010100001111 = 1001010100000000 

كما ترون ، بهذه الطريقة الصعبة نقوم بإعادة ضبط الوحدة الموجودة في أقصى اليمين إلى الصفر. كرر هذه العملية حتى نحصل على صفر نتيجة لذلك. كم عدد التكرارات ، الكثير من البتات المفردة. صحيح ، عظيم!

هذه هي الطريقة التي تتم بها كتابة هذه الخوارزمية بالكامل:

  int movesCount = 0; while (movesBits != 0) { movesBits &= (movesBits - 1); movesCount ++; } 

تم حل المشكلة!

تحتوي هذه المهمة على حل آخر بسيط للغاية ومنطقي بحت: تحديد مسافة الفارس من حافة رقعة الشطرنج (في الزاوية يوجد حركتان ، بالقرب من الحافة من 3 إلى 6 حركات ، في وسط 8 حركات). ولكن إذا أردنا حل المشكلة "وجهاً لوجه" بهذه الطريقة ، فلن نعرف عن لوحة البت ، وأقنعة البت الرأسية ، والخوارزمية لحساب بسرعة البتات الفردية والثقوب السوداء للخيول الكروية في الفراغ ...

الآن نحن نعرف كل شيء عن ذلك. أصبحت حياة مبرمج لعبة الشطرنج أكثر ثراءً وأكثر فائدة ، هتافات!

افعل ذلك بنفسك المهمة: تفعل الشيء نفسه بالنسبة لملك الشطرنج.