مونت كارلو العوامة استراتيجية التحسين

تم إعداد ترجمة المقال خصيصًا لطلاب دورة التعلم الآلي .

---

استغرق التدريب عززت عالم الذكاء الاصطناعي. بدءًا من AlphaGo و AlphaStar ، يتم الآن غزو عدد من الأنشطة التي كان يهيمن عليها البشر من قبل عملاء AI بناءً على تدريب التعزيز. باختصار ، تعتمد هذه الإنجازات على تحسين إجراءات الوكيل في بيئة معينة لتحقيق أقصى مكافأة. في المقالات القليلة الأخيرة من GradientCrescent ، بحثنا في الجوانب الأساسية المختلفة للتعليم المعزز ، من أساسيات نظم اللصوص والنهج القائمة على السياسات لتحسين السلوك القائم على المكافأة في بيئات ماركوف . كل هذه الأساليب تتطلب معرفة كاملة ببيئتنا. تتطلب البرمجة الديناميكية ، على سبيل المثال ، أن يكون لدينا توزيع احتمالي كامل لجميع انتقالات الحالة الممكنة. ومع ذلك ، في الواقع ، نجد أن معظم الأنظمة لا يمكن تفسيرها بشكل كامل ، وأنه لا يمكن الحصول على توزيعات الاحتمال بشكل صريح بسبب التعقيد أو عدم اليقين المتأصل أو قيود القدرات الحسابية. على سبيل المقارنة ، فكر في مهمة أخصائي الأرصاد الجوية - حيث يمكن أن يكون عدد العوامل المرتبطة بالتنبؤ بالطقس كبيرًا لدرجة أنه من المستحيل حساب الاحتمال بدقة.

لمثل هذه الحالات ، طرق التدريس مثل مونت كارلو هي الحل. يستخدم مصطلح مونت كارلو عادة لوصف أي نهج لتقدير العينات العشوائية. بمعنى آخر ، لا نتنبأ بالمعرفة عن بيئتنا ، لكننا نتعلم من التجربة من خلال الاطلاع على سلاسل مثالية للحالات والإجراءات والمكافآت التي تم الحصول عليها نتيجة للتفاعل مع البيئة. تعمل هذه الطرق من خلال الملاحظة المباشرة للمكافآت التي تم إرجاعها بواسطة النموذج أثناء التشغيل العادي من أجل تقدير متوسط ​​قيمة شروطه. ومن المثير للاهتمام ، حتى من دون أي معرفة بديناميات البيئة (والتي ينبغي اعتبارها توزيع احتمالية لتحولات الحالة) ، لا يزال بإمكاننا الحصول على السلوك الأمثل لتعظيم المكافآت.

على سبيل المثال ، فكر في نتيجة لفة من 12 نرد. النظر في هذه الرميات كحالة واحدة ، يمكننا متوسط ​​هذه النتائج من أجل الاقتراب من النتيجة الحقيقية المتوقعة. كلما كانت العينة أكبر ، كلما اقتربنا من النتيجة الفعلية المتوقعة بدقة أكبر.


متوسط ​​المبلغ المتوقع في 12 الزهر لمدة 60 طلقة هو 41.57

قد يبدو هذا النوع من التقييم المعتمد على أخذ العينات مألوفًا للقارئ ، حيث يتم إجراء مثل هذه العينات أيضًا لأنظمة النطاق الترددي. بدلاً من مقارنة قطاع الطرق المختلفين ، يتم استخدام طرق مونت كارلو لمقارنة السياسات المختلفة في بيئات ماركوف ، وتحديد قيمة الحالة كسياسة معينة يتم اتباعها حتى يتم الانتهاء من العمل.

تقدير مونتي كارلو لقيمة الدولة

في سياق التعلم المعزز ، تعد طرق مونت كارلو وسيلة لتقييم أهمية حالة النموذج من خلال حساب متوسط ​​نتائج العينة. بسبب الحاجة إلى حالة طرفية ، فإن طرق مونت كارلو قابلة للتطبيق بطبيعتها على البيئات العرضية. بسبب هذا القيد ، تعتبر طرق مونت كارلو عادة "مستقلة" حيث يتم تنفيذ جميع التحديثات بعد الوصول إلى الحالة النهائية. يمكن إعطاء تشبيه بسيط لإيجاد طريقة للخروج من المتاهة - فإن النهج المستقل سوف يجبر العامل على الوصول إلى النهاية قبل استخدام الخبرة الوسيطة المكتسبة من أجل محاولة تقليل الوقت الذي يستغرقه المرور في المتاهة. من ناحية أخرى ، مع النهج عبر الإنترنت ، سوف يغير الوكيل سلوكه باستمرار أثناء مرور المتاهة ، وربما يلاحظ أن الممرات الخضراء تؤدي إلى طريق مسدود وتقرر تجنبها ، على سبيل المثال. سنناقش النهج عبر الإنترنت في واحدة من المقالات التالية.

يمكن صياغة طريقة مونت كارلو على النحو التالي:



لفهم كيفية عمل طريقة مونت كارلو بشكل أفضل ، ضع في الاعتبار مخطط انتقال الحالة أدناه. يتم عرض المكافأة عن كل حالة انتقال باللون الأسود ، ويتم تطبيق عامل خصم قدره 0.5 عليها. دعونا نضع جانبا القيمة الفعلية للدولة والتركيز على حساب نتائج رمي واحد.


مخطط انتقال الحالة. يظهر رقم الحالة باللون الأحمر ، والنتيجة سوداء.
بالنظر إلى أن حالة المحطة الطرفية تُرجع نتيجة تساوي 0 ، فلنحسب نتيجة كل ولاية ، بدءًا من حالة المحطة الطرفية (G5). يرجى ملاحظة أننا قمنا بتعيين عامل الخصم على 0.5 ، مما سيؤدي إلى ترجيح نحو الحالات الأخيرة.



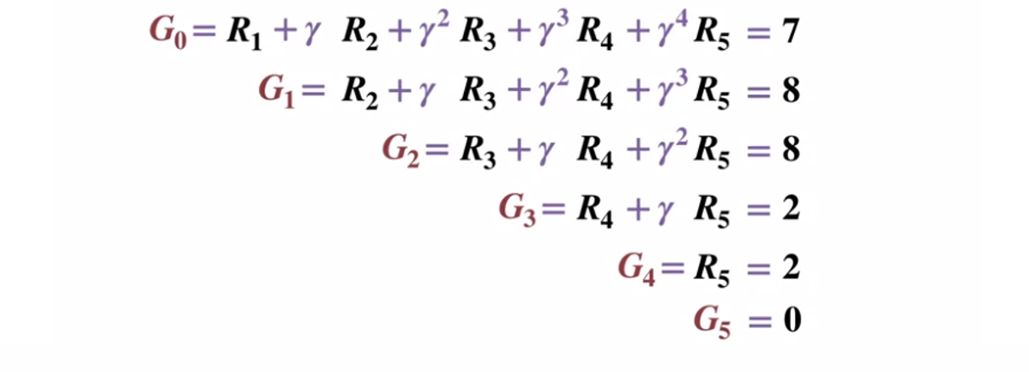
أو بشكل عام:



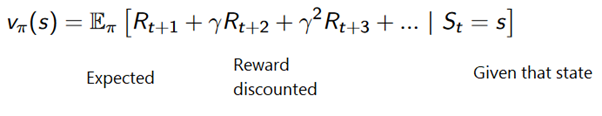
لتجنب تخزين جميع النتائج في القائمة ، يمكننا تنفيذ إجراء تحديث قيمة الحالة في طريقة مونت كارلو تدريجياً ، باستخدام معادلة لها بعض أوجه التشابه مع نزول التدرج التقليدي:


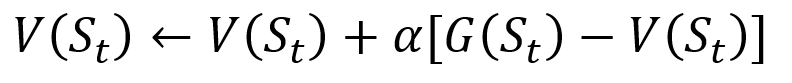مونت كارلو إجراء التحديث التدريجي. S هي الحالة ، V هي قيمتها ، G هي نتيجتها ، و A هي معلمة قيمة الخطوة.

كجزء من التدريب على التعزيز ، يمكن تصنيف طرق مونت كارلو على أنها الزيارة الأولى أو كل زيارة. باختصار ، الفرق بين الاثنين هو عدد المرات التي يمكن فيها زيارة الولاية لمرور ما قبل تحديث مونت كارلو. تقوم طريقة الزيارة الأولى في مونتي كارلو بتقدير قيمة جميع الولايات كمتوسط ​​قيمة النتائج بعد زيارات فردية لكل ولاية قبل الانتهاء ، في حين تقوم طريقة زيارة مونت كارلو كل زيارة بتقييم النتائج بعد زيارات ن حتى الانتهاء. سوف نستخدم زيارة مونت كارلو الأولى خلال هذه المقالة بسبب بساطتها النسبية.

مونت كارلو لإدارة السياسات

إذا لم يتمكن النموذج من تقديم السياسة ، فيمكن استخدام Monte Carlo لتقييم قيم إجراءات الحالة. هذا مفيد أكثر من مجرد معنى الولايات ، حيث أن فكرة معنى كل إجراء (ف) في حالة معينة تسمح للوكيل بإنشاء سياسة تلقائيًا من الملاحظات في بيئة غير مألوفة.

بشكل أكثر رسمية ، يمكننا استخدام Monte Carlo لتقدير q (s ، a ، pi) ، والنتيجة المتوقعة عند البدء من الحالة ، الإجراء a ، والسياسة اللاحقة Pi . تبقى طرق مونت كارلو كما هي ، إلا أنه يوجد بعد إضافي للإجراءات التي يتم اتخاذها لدولة معينة. من المعتقد أن زوجًا من تصرفات الحالة ( الدولة ، أ) قد تمت زيارته أثناء مرور الحالة إذا تمت زيارة الحالة على الإطلاق وتم تنفيذ الإجراء أ فيها. وبالمثل ، يمكن إجراء تقييم الإجراءات القيمة باستخدام نهجين "الزيارة الأولى" و "كل زيارة".

كما هو الحال في البرمجة الديناميكية ، يمكننا استخدام سياسة التكرار المعمم (GPI) لتشكيل سياسة من مراقبة قيم إجراءات الحالة.



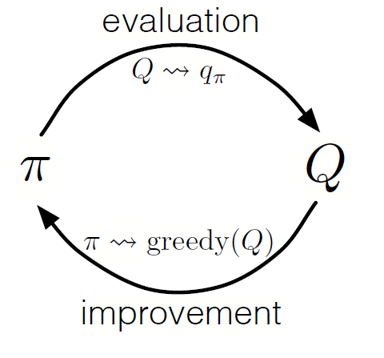
من خلال تبديل خطوات تقييم السياسة وتحسين السياسات ، بما في ذلك البحث لضمان زيارة جميع الإجراءات الممكنة ، يمكننا تحقيق السياسة المثلى لكل شرط. بالنسبة إلى Monte Carlo GPI ، يتم هذا الدوران عادة بعد نهاية كل تمريرة.


مونتي كارلو GPI

استراتيجية لعبة ورق

لفهم كيفية عمل طريقة مونت كارلو بشكل عملي في مهمة تقييم قيم الحالة المختلفة ، دعنا نلقي عرضًا تفصيليًا لمثال لعبة البلاك جاك. للبدء ، دعونا نحدد قواعد وشروط لعبتنا:

• سوف نلعب فقط ضد التاجر ، ولن يكون هناك لاعبون آخرون. سيسمح لنا ذلك بالنظر في أيدي الوكيل كجزء من البيئة.
• قيمة البطاقات ذات الأرقام المساوية للقيم الاسمية. قيمة بطاقات الصور: Jack و King و Queen هي 10. يمكن أن تكون قيمة ace 1 أو 11 حسب اختيار المشغل.
• يتلقى كلا الجانبين ورقتين. هناك ورقتان للاعبين متجهتان للأعلى ، وأحد بطاقات الموزع مقلوبة أيضًا.
• الهدف من اللعبة هو أن كمية البطاقات في متناول اليد هي <= 21. قيمة أكبر من 21 هي تمثال نصفي ، إذا كان لدى الطرفين قيمة 21 ، فسيتم لعب اللعبة بالتعادل.
• بعد أن يرى اللاعب أوراقه وبطاقة الموزع الأول ، يمكن للاعب اختيار أخذ بطاقة جديدة ("حتى الآن") أو عدمها ("كافية") حتى يشعر بالرضا عن مجموع قيم البطاقة في يده.
• ثم يعرض التاجر بطاقته الثانية - إذا كان المبلغ الناتج أقل من 17 ، فهو ملزم بأخذ بطاقات حتى يصل إلى 17 نقطة ، وبعد ذلك لا يأخذ البطاقة بعد الآن.

دعونا نرى كيف تعمل طريقة مونت كارلو مع هذه القواعد.

الجولة 1.

تكسب ما مجموعه 19. لكنك تحاول أن تمسك الحظ من جانب الذيل ، وانتهز الفرصة ، واحصل على 3 وتكسر. عندما توقفت ، كان لدى الوكيل بطاقة واحدة مفتوحة فقط بمبلغ 10. ويمكن تمثيل ذلك على النحو التالي:



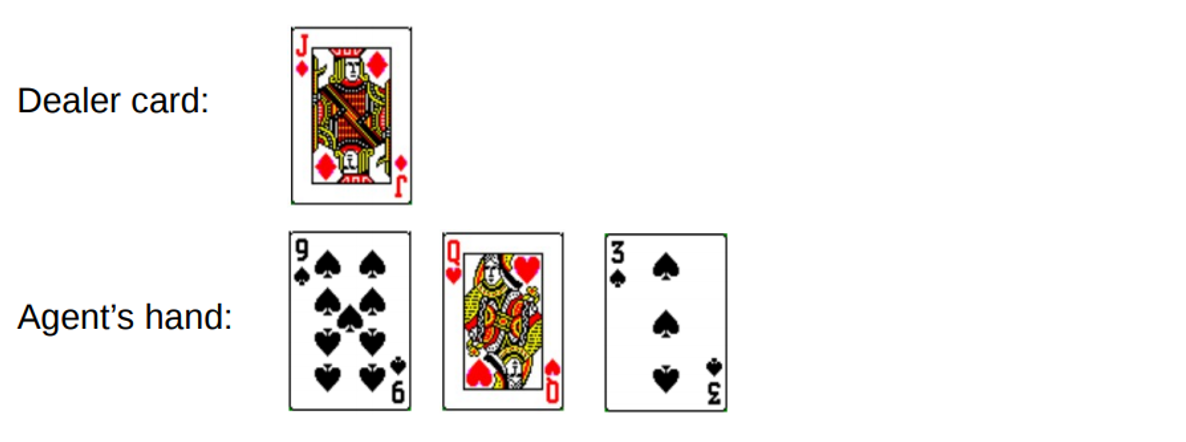
إذا توقفنا ، فإن مكافأتنا للجولة هي -1. لنقم بتعيين هذه القيمة على أنها نتيجة الإرجاع للحالة قبل الأخيرة ، باستخدام التنسيق التالي [مبلغ الوكيل ، مبلغ التاجر ، ace؟]:



حسنا ، الآن نحن محظوظون. دعنا ننتقل إلى جولة أخرى.

الجولة 2.

تكتب ما مجموعه 19. هذه المرة قررت التوقف. يطلب الوكيل رقم 13 ويأخذ بطاقة وينقطع. يمكن وصف الحالة قبل الأخيرة على النحو التالي.



دعنا نصف الشروط والمكافآت التي تلقيناها في هذه الجولة:



مع نهاية المقطع ، يمكننا الآن تحديث قيم جميع ولاياتنا في هذه الجولة باستخدام النتائج المحسوبة. إذا أخذنا عامل الخصم 1 ، فقد قمنا ببساطة بنشر مكافأة اليد الجديدة لدينا ، كما حدث مع تحولات الحالة السابقة. نظرًا لأن الحالة V (19 ، 10 ، لا) سبق إرجاعها -1 ، فنحن نحسب قيمة الإرجاع المتوقعة ونخصصها لحالتنا:


قيم الحالة النهائية للعرض باستخدام العوامه كمثال .

تطبيق

دعنا نكتب لعبة البلاك جاك باستخدام طريقة مونت كارلو التي تمت زيارتها لأول مرة لمعرفة كل قيم الحالة الممكنة (أو المجموعات المختلفة المتوفرة) في اللعبة باستخدام بيثون. سوف يستند نهجنا على نهج Sudharsan et. الله. . كالعادة ، يمكنك العثور على جميع التعليمات البرمجية من المادة على جيثب لدينا .

لتبسيط التنفيذ ، سوف نستخدم الصالة الرياضية من OpenAI. فكر في البيئة كواجهة لبدء لعبة البلاك جاك مع الحد الأدنى من الكود ، وهذا سيتيح لنا التركيز على تنفيذ التعلم المعزز. بشكل ملائم ، يتم تخزين جميع المعلومات التي تم جمعها حول الحالات والإجراءات والمكافآت في متغيرات "الملاحظة" ، والتي يتم تجميعها خلال الدورات الحالية للعبة.

لنبدأ باستيراد جميع المكتبات التي نحتاج إليها للحصول على نتائجنا وجمعها.

import gym import numpy as np from matplotlib import pyplot import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from collections import defaultdict from functools import partial %matplotlib inline plt.style.use('ggplot') 

بعد ذلك ، دعونا نهيئ بيئة الصالة الرياضية الخاصة بنا ونحدد سياسة من شأنها تنسيق إجراءات وكيلنا. في الواقع ، سوف نستمر في أخذ البطاقة حتى يصل المبلغ الموجود في اليد إلى 19 أو أكثر ، وبعد ذلك نتوقف.

 #Observation here encompassess all data about state that we need, as well as reactions to it env = gym.make('Blackjack-v0') #Define a policy where we hit until we reach 19. # actions here are 0-stand, 1-hit def sample_policy(observation): score, dealer_score, usable_ace = observation return 0 if score >= 19 else 1 

دعونا نحدد طريقة لتوليد بيانات المرور باستخدام سياستنا. سنقوم بتخزين معلومات حول الحالة والإجراءات المتخذة ومكافأة الإجراء.

 def generate_episode(policy, env): # we initialize the list for storing states, actions, and rewards states, actions, rewards = [], [], [] # Initialize the gym environment observation = env.reset() while True: # append the states to the states list states.append(observation) # now, we select an action using our sample_policy function and append the action to actions list action = sample_policy(observation) actions.append(action) # We perform the action in the environment according to our sample_policy, move to the next state observation, reward, done, info = env.step(action) rewards.append(reward) # Break if the state is a terminal state (ie done) if done: break return states, actions, rewards 

أخيرًا ، دعنا نحدد وظيفة التنبؤ لأول مرة في مونت كارلو. أولاً ، نضع قاموسًا فارغًا لتخزين قيم الحالة الحالية وقاموس يخزّن عدد السجلات لكل ولاية في مسارات مختلفة.

 def first_visit_mc_prediction(policy, env, n_episodes): # First, we initialize the empty value table as a dictionary for storing the values of each state value_table = defaultdict(float) N = defaultdict(int) 

في كل تمريرة ، ندعو طريقة create_episode الخاصة بنا للحصول على معلومات حول قيم الحالة والمكافآت المستلمة بعد حدوث الحالة. نحن أيضًا نهيئ المتغير لتخزين نتائجنا الإضافية. ثم نحصل على المكافأة وقيمة الحالة الحالية لكل ولاية تمت زيارتها أثناء التمريرة ، ونزيد عوائدنا المتغيرة بقيمة المكافأة لكل خطوة.

 for _ in range(n_episodes): # Next, we generate the epsiode and store the states and rewards states, _, rewards = generate_episode(policy, env) returns = 0 # Then for each step, we store the rewards to a variable R and states to S, and we calculate for t in range(len(states) — 1, -1, -1): R = rewards[t] S = states[t] returns += R # Now to perform first visit MC, we check if the episode is visited for the first time, if yes, #This is the standard Monte Carlo Incremental equation. # NewEstimate = OldEstimate+StepSize(Target-OldEstimate) if S not in states[:t]: N[S] += 1 value_table[S] += (returns — value_table[S]) / N[S] return value_table 

واسمحوا لي أن أذكرك بأنه بما أننا ننفذ الزيارة الأولى لمونتي كارلو ، فإننا نزور ولاية واحدة مرة واحدة. لذلك ، نحن نقوم بفحص مشروط في قاموس الحالة لمعرفة ما إذا كانت الحالة قد تمت زيارتها. إذا تم استيفاء هذا الشرط ، يمكننا حساب القيمة الجديدة باستخدام الإجراء المحدد مسبقًا لتحديث قيم الحالة باستخدام طريقة مونت كارلو وزيادة عدد الملاحظات لهذه الحالة بمقدار 1. ثم نكرر العملية للتمرير التالي من أجل الحصول في نهاية المطاف على متوسط ​​قيمة النتيجة .

دعنا ندير ما حصلنا عليه وننظر في النتائج!

 value = first_visit_mc_prediction(sample_policy, env, n_episodes=500000) for i in range(10): print(value.popitem()) 

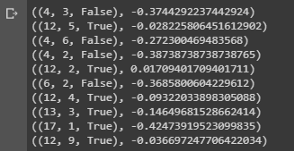خاتمة عينة توضح قيم الحالة لمختلف المجموعات على يديك في لعبة ورق.

يمكننا الاستمرار في إجراء ملاحظات مونت كارلو لـ 5000 تمريرة وبناء توزيع لقيم الحالة التي تصف قيم أي مجموعة في أيدي اللاعب والتاجر.

 def plot_blackjack(V, ax1, ax2): player_sum = np.arange(12, 21 + 1) dealer_show = np.arange(1, 10 + 1) usable_ace = np.array([False, True]) state_values = np.zeros((len(player_sum), len(dealer_show), len(usable_ace))) for i, player in enumerate(player_sum): for j, dealer in enumerate(dealer_show): for k, ace in enumerate(usable_ace): state_values[i, j, k] = V[player, dealer, ace] X, Y = np.meshgrid(player_sum, dealer_show) ax1.plot_wireframe(X, Y, state_values[:, :, 0]) ax2.plot_wireframe(X, Y, state_values[:, :, 1]) for ax in ax1, ax2: ax.set_zlim(-1, 1) ax.set_ylabel('player sum') ax.set_xlabel('dealer sum') ax.set_zlabel('state-value') fig, axes = pyplot.subplots(nrows=2, figsize=(5, 8),subplot_kw={'projection': '3d'}) axes[0].set_title('state-value distribution w/o usable ace') axes[1].set_title('state-value distribution w/ usable ace') plot_blackjack(value, axes[0], axes[1]) 

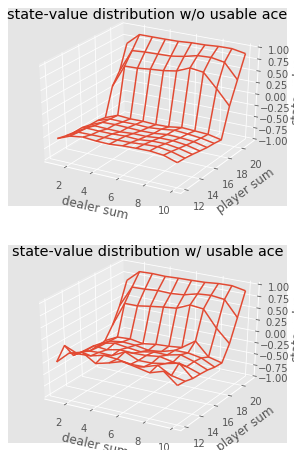تصور لقيم الدولة من مجموعات مختلفة في لعبة ورق.

لذلك ، دعونا نلخص ما تعلمناه.

• تتيح لنا أساليب التعلم القائمة على أخذ العينات تقييم قيم الحالة وحالة الإجراء دون أي ديناميات انتقالية ، وذلك ببساطة عن طريق أخذ العينات.
• تعتمد مناهج مونت كارلو على أخذ عينات عشوائية من النموذج ، ومراقبة المكافآت التي يتم إرجاعها بواسطة النموذج ، وجمع المعلومات أثناء التشغيل العادي لتحديد متوسط ​​قيمة حالاته.
• باستخدام أساليب مونت كارلو ، يمكن اتباع سياسة التكرار المعمم.
• يمكن تقدير قيمة جميع التوليفات الممكنة بين يدي اللاعب والتاجر في لعبة البلاك جاك باستخدام العديد من عمليات محاكاة مونت كارلو ، مما يمهد الطريق لاستراتيجيات محسنة.

بهذا نختتم مقدمة طريقة مونت كارلو. في مقالتنا التالية ، سوف ننتقل إلى طرق التدريس في نموذج تعلم الفرق الزمني.

مصادر:

سوتون وآخرون. al ، تعزيز التعلم
وايت وآخرون. آل ، أساسيات التعلم التعزيز ، جامعة ألبرتا
سيلفا وآخرون. al ، التعلم التعزيز ، UCL
بلات وآخرون. آل ، جامعة الشمال الشرقي

هذا كل شيء. أراك في الدورة !