يُعد تحسين برامج التحويل البرمجي أساس البرامج الحديثة: فهي تتيح للمبرمجين كتابة التعليمات البرمجية بلغة يفهمونها ، ثم تحويلها إلى رمز يمكن تنفيذه بكفاءة بواسطة المعدات. تتمثل مهمة تحسين برامج التحويل البرمجي في فهم ما يفعله برنامج الإدخال الذي كتبته وإنشاء برنامج إخراج يقوم بنفس الشيء ، ولكن بشكل أسرع فقط.
في هذه المقالة ، سوف نلقي نظرة على بعض تقنيات الاستدلال الأساسية في تحسين المترجمين: كيفية تصميم برنامج يمكن للمترجم العمل به بسهولة ؛ ما التخفيضات التي يمكن إجراؤها في البرنامج وكيفية استخدامها لتقليله والتعجيل به.
يمكن تنفيذ برامج تحسين الأداء في أي مكان: كخطوة في عملية تجميع كبيرة (
Scala Optimizer ) ؛ كبرنامج منفصل ، تم إطلاقه بعد برنامج التحويل البرمجي وقبل التنفيذ (
Proguard ) ؛ أو كجزء من بيئة وقت التشغيل التي تحسن البرنامج أثناء تنفيذه (
مترجم JVM JIT ). تختلف القيود المفروضة على عمل المُحسِّن اعتمادًا على الموقف ، ولكن لديهم مهمة واحدة: أخذ برنامج الإدخال وتحويله إلى الإخراج ، والذي يقوم بنفس الشيء ، ولكن بشكل أسرع.
أولاً ، سوف نلقي نظرة على بعض الأمثلة على التحسينات لمشروع المسودة حتى تفهم ما تفعله أدوات التحسين عادةً وكيفية القيام بذلك يدويًا. بعد ذلك سننظر في عدة طرق لتقديم البرامج ، وأخيراً سنحلل الخوارزميات والتقنيات التي يمكنك من خلالها تحليل البرامج ونجعلها أصغر وأسرع.
مشروع البرنامج
سيتم إعطاء جميع الأمثلة في Java. هذه اللغة شائعة جدًا وتجميعها في مجمع بسيط نسبيًا -
Java Bytecode . لذلك سننشئ أساسًا جيدًا ، بفضله يمكننا استكشاف تقنيات تحسين الترجمة باستخدام أمثلة حقيقية قابلة للتنفيذ. جميع التقنيات الموضحة أدناه قابلة للتطبيق في جميع لغات البرمجة الأخرى تقريبًا.
أولا ، النظر في مشروع البرنامج. أنه يحتوي على منطق مختلف ، يسجل النتيجة القياسية داخل العملية وإرجاع النتيجة المحسوبة. البرنامج نفسه غير منطقي ، ولكن سيتم استخدامه كتوضيح لما يمكن تحسينه مع الحفاظ على السلوك الحالي:
static int main(int n){ int count = 0, total = 0, multiplied = 0; Logger logger = new PrintLogger(); while(count < n){ count += 1; multiplied *= count; if (multiplied < 100) logger.log(count); total += ackermann(2, 2); total += ackermann(multiplied, n); int d1 = ackermann(n, 1); total += d1 * multiplied; int d2 = ackermann(n, count); if (count % 2 == 0) total += d2; } return total; }
في الوقت الحالي ، نفترض أن هذا البرنامج هو كل ما لدينا ، ولا توجد أجزاء أخرى من الكود تسميه. إنه ببساطة إدخال البيانات في
main ، وتنفيذ ، وإرجاع النتيجة. الآن دعونا تحسين هذا البرنامج.
أمثلة التحسين
اكتب الصب والمضمنة
ربما لاحظت أن متغير
logger له نوع غير دقيق: على الرغم من تسمية
Logger ، بناءً على الكود ، يمكننا أن نستنتج أن هذه فئة فرعية محددة -
PrintLogger :
- Logger logger = new PrintLogger(); + PrintLogger logger = new PrintLogger();
نحن نعلم الآن أن
logger هو
PrintLogger ، ونعلم أن استدعاء
logger.log يمكن أن يكون له تطبيق واحد. يمكنك مضمنة:
- if (multiplied < 100) logger.logcount(); + if (multiplied < 100) System.out.println(count);
سيؤدي ذلك إلى تقليل البرنامج عن طريق إزالة فئة
ErrLogger غير الضرورية ، والتي لا يتم استخدامها ، وكذلك عن طريق حذف الطرق المختلفة
log public Logger ، نظرًا لأننا نقوم بتضمينها في مكان واحد من المكالمة.
ثوابت التخثر
أثناء تنفيذ البرنامج ، لا يتم
count total والتغيير
total ، ولكن: يتم ضربه عند
0 ويتم ضربه في كل مرة من خلال
multiplied = multiplied * count ،
multiplied = multiplied * count المتبقي يساوي
0 . لذلك ، يمكنك استبداله في البرنامج بأكمله برقم
0 :
static int main(int n){ - int count = 0, total = 0, multiplied = 0; + int count = 0, total = 0; PrintLogger logger = new PrintLogger(); while(count < n){ count += 1; - multiplied *= count; - if (multiplied < 100) System.out.println(count); + if (0 < 100) logger.log(count); total += ackermann(2, 2); - total += ackermann(multiplied, n); + total += ackermann(0, n); int d1 = ackermann(n, 1); - total += d1 * multiplied; int d2 = ackermann(n, count); if (count % 2 == 0) total += d2; } return total; }
نتيجة لذلك ، نرى أن
d1 * multiplied دائمًا
0 ، مما يعني أن
total += d1 * multiplied لا يفعل شيئًا ويمكن حذفه:
- total += d1 * multiplied
إزالة قانون الموتى
بعد طي
multiplied وإدراك أن
total += d1 * multiplied لا يفعل شيئًا ، يمكنك إزالة تعريف
int d1 :
- int d1 = ackermann(n, 1);
لم يعد هذا جزءًا من البرنامج ، ولأن
ackermann هي وظيفة محض ، فلن يؤثر إلغاء التثبيت على نتيجة البرنامج.
وبالمثل ، بعد تضمين
logger.log ، لم يعد يتم استخدام
logger نفسه ويمكن إزالته:
- PrintLogger logger = new PrintLogger();
إزالة فرع
الآن يعتمد الانتقال الشرطي الأول في دورتنا على
0 < 100 . نظرًا لأن هذا صحيح دائمًا ، يمكنك ببساطة إزالة الشرط:
- if (0 < 100) System.out.println(count); + System.out.println(count);
أي انتقال مشروط يكون دائمًا صحيحًا يمكن أن يكون مضمّنًا في نص الشرط ، وبالنسبة للتحولات غير الصحيحة دائمًا ، يمكنك حذف الشرط مع نصه.
حساب جزئي
نحلل الآن المكالمات الثلاثة المتبقية إلى
ackermann :
total += ackermann(2, 2); total += ackermann(0, n); int d2 = ackermann(n, count);
- الأول له حجتان ثابتتان. الوظيفة نقية ، وعند الحساب الأولي
ackermann(2, 2) يجب أن تساوي 7. - تحتوي المكالمة الثانية على وسيطة ثابتة واحدة
0 و n غير معروفة. يمكنك تمريرها إلى تعريف ackermann ، وتبين أنه عندما تكون m 0 ، تُرجع الدالة دائمًا n + 1.
- في المكالمة الثالثة ، كلا الوسيطتين غير معروفتين:
n count . دعنا نتركهم في المكان الآن.
بالنظر إلى أن الدعوة إلى
ackermann تُعرَّف على النحو التالي:
static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); }
يمكنك تبسيطها إلى:
- total += ackermann(2, 2); + total += 7 - total += ackermann(0, n); + total += n + 1 int d2 = ackermann(n, count);
جدولة متأخرة
يتم استخدام تعريف
d2 فقط في
if (count % 2 == 0) الشرطية
if (count % 2 == 0) . نظرًا لأن عملية حساب
ackermann نظيفة ، يمكنك نقل هذه المكالمة إلى
ackermann مشروط حتى لا تتم معالجتها حتى يتم استخدامها:
- int d2 = ackermann(n, count); - if (count % 2 == 0) total += d2; + if (count % 2 == 0) { + int d2 = ackermann(n, count); + total += d2; + }
سيؤدي ذلك إلى تجنب نصف المكالمات إلى
ackermann(n, count) ، والإسراع في تنفيذ البرنامج.
للمقارنة ، فإن وظيفة
System.out.println ليست نظيفة ، مما يعني أنه لا يمكن نقلها داخل أو خارج القفزات الشرطية دون تغيير دلالات البرنامج.
النتيجة المحسنة
بعد جمع كل التحسينات ، نحصل على شفرة المصدر التالية:
static int main(int n){ int count = 0, total = 0; while(count < n){ count += 1; System.out.println(count); total += 7; total += n + 1; if (count % 2 == 0) { total += d2; int d2 = ackermann(n, count); } } return total; } static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); }
على الرغم من أننا قمنا بتحسينه يدويًا ، إلا أن كل هذا يمكن القيام به تلقائيًا. فيما يلي النتيجة المحذوفة لمحسن النموذج الأولي الذي كتبته لبرامج JVM:
static int main(int var0) { new Demo.PrintLogger(); int var1 = 0; int var3; for(int var2 = 0; var2 < var0; var2 = var3) { System.out.println(var3 = 1 + var2); int var10000 = var3 % 2; int var7 = var1 + 7 + var0 + 1; var1 = var10000 == 0 ? var7 + ackermann(var0, var3) : var7; } return var1; } static int ackermann__I__TI1__I(int var0) { if (var0 == 0) return 2; else return ackermann(var0 - 1, var0 == 0 ? 1 : ackermann__I__TI1__I(var0 - 1);); } static int ackermann(int var0, int var1) { if (var0 == 0) return var1 + 1; else return var1 == 0 ? ackermann__I__TI1__I(var0 - 1) : ackermann(var0 - 1, ackermann(var0, var1 - 1)); } static class PrintLogger implements Demo.Logger {} interface Logger {}
يختلف رمز فك الشفرة قليلاً عن الإصدار المحسن يدويًا. شيء لم يتمكن المحول البرمجي من تحسينه (على سبيل المثال ، مكالمة غير مستخدمة لـ
new PrintLogger ) ، ولكن تم إجراء شيء مختلف قليلاً (على سبيل المثال ،
ackermann__I__TI1__I new PrintLogger ). لكن بالنسبة للباقي ، قام المحسن التلقائي بنفس الشيء الذي قمت به ، وذلك باستخدام المنطق المضمن فيه.
السؤال الذي يطرح نفسه: كيف؟
وجهات النظر المتوسطة
إذا حاولت إنشاء مُحسِّن خاص بك ، فربما يكون السؤال الأول الذي يطرح نفسه هو الأكثر أهمية: ما هو "البرنامج"؟
لا شك أنك معتاد على كتابة البرامج وتغييرها في شكل شفرة المصدر. أنت بالتأكيد تنفيذها في شكل ثنائيات المترجمة ، وربما تصحيح الثنائيات. قد تكون صادفتك برامج في شكل
شجرة بناء جملة أو
رمز مكون من ثلاثة عناوين أو
A-Normal أو
نمط مرور مستمر أو
تعيين ثابت واحد .
هناك حديقة حيوان كاملة من تمثيلات مختلفة للبرامج. سنناقش هنا أهم الطرق لتمثيل "البرنامج" داخل المُحسِّن.
شفرة المصدر
static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); }
شفرة المصدر غير المترجمة تمثل أيضًا برنامجك. إنه صغير نسبيًا ، يمكن قراءته من قِبل الإنسان ، لكن له عيبان:
- يحتوي الكود المصدري على جميع تفاصيل الأسماء والتنسيق ، والتي تعتبر مهمة للمبرمج ، ولكنها غير مجدية للكمبيوتر.
- تعد البرامج الخاطئة في شكل شفرة المصدر أكثر عددًا من البرامج الصحيحة ، وأثناء عملية التحسين ، تحتاج إلى التأكد من تحويل البرنامج من رمز مصدر الإدخال الصحيح إلى شفرة مصدر الإخراج الصحيحة.
هذه العوامل تجعل من الصعب للمحسن العمل مع البرنامج في شكل شفرة المصدر. نعم ، يمكنك تحويل مثل هذا البرنامج ، على سبيل المثال ، باستخدام
التعبيرات العادية لتحديد واستبدال الأنماط. ومع ذلك ، فإن أول عاملين يجعل من الصعب تحديد أنماط موثوق بها مع وفرة من التفاصيل الدخيلة. والعامل الثاني يزيد بشكل كبير من فرصة الخلط والحصول على برنامج غير صحيح.
هذه القيود مقبولة لمحولات البرامج التي يتم تنفيذها تحت إشراف بشري ، على سبيل المثال ، عندما يمكنك استخدام
Codemod لإعادة
تشكيل وتحويل قاعدة الشفرة. ومع ذلك ، لا يمكنك استخدام التعليمات البرمجية المصدر كنموذج أساسي للمحسن التلقائي.
بناء جملة الأشجار
static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); } IfElse( cond = BinOp(Ident("m"), "=", Literal(0)), then = Return(BinOp(Ident("n"), "+", Literal(1)), else = IfElse( cond = BinOp(Ident("n"), "=", Literal(0)), then = Return(Call("ackermann", BinOp(Ident("m"), "-", Literal(1)), Literal(1)), else = Return( Call( "ackermann", BinOp(Ident("m"), "-", Literal(1)), Call("ackermann", Ident("m"), BinOp(Ident("n"), "-", Literal(1))) ) ) ) )

ملخص بناء الجملة الأشجار (AST) هو تنسيق وسيطة شائعة أخرى. توجد في الخطوة التالية من سلم التجريد مقارنةً بالكود المصدري. عادةً ما يتجاهل AST جميع تنسيقات التعليمات البرمجية المصدر والمسافة البادئة والتعليقات ، لكنه يحتفظ بأسماء المتغيرات المحلية التي يتم تجاهلها في تمثيلات أكثر تجريدية.
مثل شفرة المصدر ، تعاني AST من إمكانية تشفير المعلومات غير الضرورية التي لا تؤثر على الدلالات الفعلية للبرنامج. على سبيل المثال ، أجزاء شفرتي التعليمات البرمجية التاليتين متطابقتان نصف دلالة ؛ أنها تختلف فقط في أسماء المتغيرات المحلية ، ولكن لا يزال لديهم ASTs مختلفة:
static int ackermannA(int m, int n){ int p = n; int q = m; if (q == 0) return p + 1; else if (p == 0) return ackermannA(q - 1, 1); else return ackermannA(q - 1, ackermannA(q, p - 1)); } Block( Assign("p", Ident("n")), Assign("q", Ident("m")), IfElse( cond = BinOp(Ident("q"), "==", Literal(0)), then = Return(BinOp(Ident("p"), "+", Literal(1)), else = IfElse( cond = BinOp(Ident("p"), "==", Literal(0)), then = Return(Call("ackermann", BinOp(Ident("q"), "-", Literal(1)), Literal(1)), else = Return( Call( "ackermann", BinOp(Ident("q"), "-", Literal(1)), Call("ackermann", Ident("q"), BinOp(Ident("p"), "-", Literal(1))) ) ) ) ) ) static int ackermannB(int m, int n){ int r = n; int s = m; if (s == 0) return r + 1; else if (r == 0) return ackermannB(s - 1, 1); else return ackermannB(s - 1, ackermannB(s, r - 1)); } Block( Assign("r", Ident("n")), Assign("s", Ident("m")), IfElse( cond = BinOp(Ident("s"), "==", Literal(0)), then = Return(BinOp(Ident("r"), "+", Literal(1)), else = IfElse( cond = BinOp(Ident("r"), "==", Literal(0)), then = Return(Call("ackermann", BinOp(Ident("s"), "-", Literal(1)), Literal(1)), else = Return( Call( "ackermann", BinOp(Ident("s"), "-", Literal(1)), Call("ackermann", Ident("s"), BinOp(Ident("r"), "-", Literal(1))) ) ) ) ) )
النقطة الأساسية هي أنه على الرغم من أن AST لها بنية شجرة ، فإنها تحتوي على العقد التي تتصرف بشكل شبه لا يشبه الأشجار: يتم تحديد قيم
Ident("r") و
Ident("s") ليس بمحتويات الأشجار الفرعية الخاصة بها ، ولكن بواسطة العقد upstream
Assign("r", ...) upstream
Assign("r", ...) وتعيين
Assign("s", ...) . في الواقع ، هناك علاقات دلالات إضافية بين
Ident Assign التي لا تقل أهمية عن الحواف في بنية شجرة AST:

تشكل هذه الوصلات بنية بيانية معممة ، بما في ذلك الدورات في وجود تعريفات متكررة للوظائف.
بايت كود
نظرًا لأننا اخترنا Java كلغة رئيسية ، يتم حفظ البرامج المترجمة على أنها Java bytecode في ملفات .class.
أذكر وظيفة
ackermann لدينا:
static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); }
يتم تجميع هذا الرمز الفرعي:
0: iload_0 1: ifne 8 4: iload_1 5: iconst_1 6: iadd 7: ireturn 8: iload_1 9: ifne 20 12: iload_0 13: iconst_1 14: isub 15: iconst_1 16: invokestatic ackermann:(II)I 19: ireturn 20: iload_0 21: iconst_1 22: isub 23: iload_0 24: iload_1 25: iconst_1 26: isub 27: invokestatic ackermann:(II)I 30: invokestatic ackermann:(II)I 33: ireturn
تعد Java Virtual Machine (JVM) ، التي تشغل كود Java المزدوج ، عبارة عن مجموعة من المكدس والتسجيلات: هناك مجموعة معاملات (STACK) يتم فيها التعامل مع القيم ، ومجموعة من المتغيرات المحلية (LOCALS) يمكن تخزين هذه القيم فيها. تبدأ الوظيفة بمعلمات N في فتحات N الأولى للمتغيرات المحلية. عند تنفيذها ، تنقل الوظيفة البيانات إلى المكدس ، وتعمل عليها ، وتعيدها إلى المتغيرات ، وتدعو إلى إرجاع القيمة إلى المتصل من مكدس المعامل.
إذا قمت بكتابة تعليق توضيحي للرمز الجانبي أعلاه لتمثيل القيم التي تتحرك بين المكدس والجدول المتغير المحلي ، فسيبدو كما يلي:
BYTECODE LOCALS STACK |a0|a1| | 0: iload_0 |a0|a1| |a0| 1: ifne 8 |a0|a1| | 4: iload_1 |a0|a1| |a1| 5: iconst_1 |a0|a1| |a1| 1| 6: iadd |a0|a1| |v1| 7: ireturn |a0|a1| | 8: iload_1 |a0|a1| |a1| 9: ifne 20 |a0|a1| | 12: iload_0 |a0|a1| |a0| 13: iconst_1 |a0|a1| |a0| 1| 14: isub |a0|a1| |v2| 15: iconst_1 |a0|a1| |v2| 1| 16: invokestatic ackermann:(II)I |a0|a1| |v3| 19: ireturn |a0|a1| | 20: iload_0 |a0|a1| |a0| 21: iconst_1 |a0|a1| |a0| 1| 22: isub |a0|a1| |v4| 23: iload_0 |a0|a1| |v4|a0| 24: iload_1 |a0|a1| |v4|a0|a1| 25: iconst_1 |a0|a1| |v4|a0|a1| 1| 26: isub |a0|a1| |v4|a0|v5| 27: invokestatic ackermann:(II)I |a0|a1| |v4|v6| 30: invokestatic ackermann:(II)I |a0|a1| |v7| 33: ireturn |a0|a1| |
هنا ، باستخدام
a0 و
a1 قدمت الوسائط إلى الدالة ، والتي يتم تخزينها في جدول LOCALS في بداية الوظيفة.
1 يمثل الثوابت المحملة عبر
iconst_1 ، ومن
v1 إلى
v7 ، القيم المتوسطة المحسوبة. هناك ثلاثة تعليمات
ireturn تعود
v1 و
v3 و
v7 . لا تقوم هذه الوظيفة بتعريف المتغيرات المحلية الأخرى ، لذلك تقوم صفيف LOCALS بتخزين وسيطات الإدخال فقط.
أعلاه ، رأينا نوعين مختلفين من
ackermannA -
ackermannA و
ackermannB . لذلك ينظرون في bytecode:
BYTECODE LOCALS STACK |a0|a1| | 0: iload_1 |a0|a1| |a1| 1: istore_2 |a0|a1|a1| | 2: iload_0 |a0|a1|a1| |a0| 3: istore_3 |a0|a1|a1|a0| | 4: iload_3 |a0|a1|a1|a0| |a0| 5: ifne 12 |a0|a1|a1|a0| | 8: iload_2 |a0|a1|a1|a0| |a1| 9: iconst_1 |a0|a1|a1|a0| |a1| 1| 10: iadd |a0|a1|a1|a0| |v1| 11: ireturn |a0|a1|a1|a0| | 12: iload_2 |a0|a1|a1|a0| |a1| 13: ifne 24 |a0|a1|a1|a0| | 16: iload_3 |a0|a1|a1|a0| |a0| 17: iconst_1 |a0|a1|a1|a0| |a0| 1| 18: isub |a0|a1|a1|a0| |v2| 19: iconst_1 |a0|a1|a1|a0| |v2| 1| 20: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v3| 23: ireturn |a0|a1|a1|a0| | 24: iload_3 |a0|a1|a1|a0| |a0| 25: iconst_1 |a0|a1|a1|a0| |a0| 1| 26: isub |a0|a1|a1|a0| |v4| 27: iload_3 |a0|a1|a1|a0| |v4|a0| 28: iload_2 |a0|a1|a1|a0| |v4|a0|a1| 29: iconst_1 |a0|a1|a1|a0| |v4|a0|a1| 1| 30: isub |a0|a1|a1|a0| |v4|a0|v5| 31: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v4|v6| 34: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v7| 37: ireturn |a0|a1|a1|a0| |
نظرًا لأن الكود المصدري يأخذ وسيطين ويضعهما في المتغيرات المحلية ، فإن كود الكود يحتوي على الإرشادات المقابلة لتحميل قيم الوسيطة من الفهارس المحلية 0 و 1 وحفظها تحت الفهارس 2 و 3. ومع ذلك ، فإن الكود الثنائي غير مهتم بأسماء المتغيرات المحلية: بواسطتهم حصرا كما هو الحال مع الفهارس في مجموعة LOCALS. لذلك ، سيكون
ackermannB و
ackermannB لهما رموزًا متطابقة. هذا منطقي ، لأنهم متساوون معنويا!
ومع ذلك ، لا يتم تجميع
ackermannA و
ackermannB في نفس الرمز الفرعي مثل
ackermann الأصلي: على الرغم من أن الرمز الفرعي المستخلص من أسماء المتغيرات المحلية ، فإنه لا يزال غير مجردة تمامًا من التحميل والحفظ من / إلى هذه المتغيرات. لا يزال من المهم بالنسبة لنا كيف تتحرك القيم على طول LOCALS و STACK ، على الرغم من أنها لا تؤثر على السلوك الفعلي للبرنامج.
بالإضافة إلى الافتقار إلى التجريد من التحميل / الادخار ، فإن الكود الجانبي له عيب آخر: مثل معظم المجمعات الخطية ، فهو مثالي للغاية من حيث الاكتناز ، وقد يكون من الصعب للغاية تعديله عندما يتعلق الأمر بالتحسينات.
لجعله أكثر وضوحًا ، دعنا ننظر إلى
ackermann لوظيفة
ackermann الأصلية:
BYTECODE LOCALS STACK |a0|a1| | 0: iload_0 |a0|a1| |a0| 1: ifne 8 |a0|a1| | 4: iload_1 |a0|a1| |a1| 5: iconst_1 |a0|a1| |a1| 1| 6: iadd |a0|a1| |v1| 7: ireturn |a0|a1| | 8: iload_1 |a0|a1| |a1| 9: ifne 20 |a0|a1| | 12: iload_0 |a0|a1| |a0| 13: iconst_1 |a0|a1| |a0| 1| 14: isub |a0|a1| |v2| 15: iconst_1 |a0|a1| |v2| 1| 16: invokestatic ackermann:(II)I |a0|a1| |v3| 19: ireturn |a0|a1| | 20: iload_0 |a0|a1| |a0| 21: iconst_1 |a0|a1| |a0| 1| 22: isub |a0|a1| |v4| 23: iload_0 |a0|a1| |v4|a0| 24: iload_1 |a0|a1| |v4|a0|a1| 25: iconst_1 |a0|a1| |v4|a0|a1| 1| 26: isub |a0|a1| |v4|a0|v5| 27: invokestatic ackermann:(II)I |a0|a1| |v4|v6| 30: invokestatic ackermann:(II)I |a0|a1| |v7| 33: ireturn |a0|a1| |
لنقم بإجراء تغيير تقريبي: دع الدالة تستدعي
30: invokestatic ackermann:(II)I لا أستخدم الوسيطة الأولى. وبعد ذلك ، يمكن استبدال هذه المكالمة بـ المكالمة المكافئة
30: invokestatic ackermann2:(I)I ، والتي تأخذ وسيطة واحدة فقط. هذا تحسين شائع ، والذي يسمح باستخدام "إزالة الكود الميت"
30: invokestatic ackermann:(II)I أي كود يستخدم لحساب الوسيطة الأولى
30: invokestatic ackermann:(II)Iللقيام بذلك ، لا نحتاج فقط إلى استبدال التعليمة
30 ، بل نحتاج أيضًا إلى إلقاء نظرة على قائمة الإرشادات وفهم مكان احتساب الوسيطة الأولى (
v4 في
STACK ) ، وكذلك حذفها. نعود من التعليمات من
30 إلى
22 ومن
22 إلى
21 و
20 . النسخة النهائية:
BYTECODE LOCALS STACK |a0|a1| | 0: iload_0 |a0|a1| |a0| 1: ifne 8 |a0|a1| | 4: iload_1 |a0|a1| |a1| 5: iconst_1 |a0|a1| |a1| 1| 6: iadd |a0|a1| |v1| 7: ireturn |a0|a1| | 8: iload_1 |a0|a1| |a1| 9: ifne 20 |a0|a1| | 12: iload_0 |a0|a1| |a0| 13: iconst_1 |a0|a1| |a0| 1| 14: isub |a0|a1| |v2| 15: iconst_1 |a0|a1| |v2| 1| 16: invokestatic ackermann:(II)I |a0|a1| |v3| 19: ireturn |a0|a1| | - 20: iload_0 |a0|a1| | - 21: iconst_1 |a0|a1| | - 22: isub |a0|a1| | 23: iload_0 |a0|a1| |a0| 24: iload_1 |a0|a1| |a0|a1| 25: iconst_1 |a0|a1| |a0|a1| 1| 26: isub |a0|a1| |a0|v5| 27: invokestatic ackermann:(II)I |a0|a1| |v6| - 30: invokestatic ackermann:(II)I |a0|a1| |v7| + 30: invokestatic ackermann2:(I)I |a0|a1| |v7| 33: ireturn |a0|a1| |
لا يزال بإمكاننا إجراء مثل هذا التغيير البسيط إلى وظيفة
ackermann بسيطة. ولكن في الوظائف الكبيرة المستخدمة في المشاريع الحقيقية ، سيكون من الصعب إجراء العديد من التغييرات المترابطة. بشكل عام ، قد يتطلب أي تغيير صغير في برنامجك تغييرات عديدة في جميع أنحاء كود البايت.
قد تلاحظ أننا أجرينا التغيير الموضح أعلاه من خلال تحليل القيم في LOCALS و STACK: لقد شاهدنا كيف
v4 تمرير الإصدار
v4 إلى التعليمة
30 من التعليمات
22 ، و
22 يأخذ البيانات إلى
a0 و
1 ، والتي تأتي من الإرشادات
21 و
20 . يتم نقل هذه القيم بين LOCALS و STACK وفقًا لمبدأ الرسم البياني: من التعليمات التي تحسب القيمة إلى مكان استخدامها الإضافي.
مثل أزواج
Ident /
Assign في ASTs الخاصة بنا ، فإن القيم التي يتم تمريرها بين LOCALS و STACK تشكل رسمًا بيانيًا بين نقاط حساب القيم ونقاط استخدامها. فلماذا لا نبدأ العمل مباشرة مع الرسم البياني؟
الرسوم البيانية تدفق البيانات
الرسوم البيانية تدفق البيانات هي المستوى التالي من التجريد بعد bytecode. إذا قمنا بتوسيع شجرة بناء الجملة الخاصة بنا مع علاقات
Ident /
Assign ، أو إذا كنا نتتبع كيفية قيام bytecode بنقل القيم بين LOCALS و STACK ، فيمكننا إنشاء رسم بياني. لوظيفة
ackermann يبدو كما يلي:

بخلاف الرمز الترويجي AST أو Java ، لا تستخدم الرسوم البيانية لتدفق البيانات مفهوم "المتغير المحلي": بدلاً من ذلك ، يحتوي الرسم البياني على اتصالات مباشرة بين كل قيمة ومكان استخدامها. عند تحليل الرمز الفرعي ، غالبًا ما يكون من الضروري تفسير LOCALS و STACK بشكل تجريدي لفهم كيفية تحرك القيم ؛ يتضمن تحليل AST تتبع الشجرة والعمل مع جدول الرموز الذي يحتوي على اقترانات
Assign /
Ident ؛ غالبًا ما يكون تحليل الرسوم البيانية لتدفق البيانات وتحليلها عبارة عن تتبع مباشر للتحولات - الفكرة الخالصة عن "نقل القيم" دون قشور تقديم البرنامج.
ackermann السهل معالجة
ackermann أكثر من الرمز
ackermann الخطي: استبدال العقدة باستدعاء
ackermann باستدعاء
ackermann ackermann2 إحدى الوسيطات هو مجرد تغيير عقدة الرسم البياني (باللون الأخضر) وحذف إحدى روابط الإدخال إلى جانب عقد النقل (باللون الأحمر):

كما ترون ، فإن التغيير الطفيف في البرنامج (استبدال
ackermann(int n, int m) بـ
ackermann2(int m) ) يتحول إلى تغيير موضعي نسبيًا في الرسم البياني لدفق البيانات.
بشكل عام ، يعد العمل باستخدام الرسوم البيانية أسهل بكثير من استخدام الرمز الثنائي الخطي أو AST: فهي سهلة التحليل والتغيير.
لا يوجد الكثير من التفاصيل في هذا الوصف للرسوم البيانية: بالإضافة إلى التمثيل الفعلي الفعلي للرسم البياني ، هناك العديد من الطرق الأخرى لنمذجة الحالة والتحكم في التدفق ، والتي يصعب التعامل معها في نطاق المقالة وخارجها. لقد حذفت أيضًا عددًا من التفاصيل حول تحويل الرسوم البيانية ، على سبيل المثال ، إضافة الروابط وإزالتها ، والانتقال إلى الأمام والخلف ، والتحولات الأفقية والعمودية (في العرض والعمق) ، وما إلى ذلك. إذا درست الخوارزميات ، فيجب أن يكون كل هذا مألوفًا لك .
أخيرًا ، تم حذف خوارزميات التحويل من الكود الثنائي الخطي إلى الرسم البياني ، ثم من الرسم البياني إلى الكود الثنائي. هذه في حد ذاتها مهمة مثيرة للاهتمام ، لكننا نتركها لك للدراسة المستقلة.
تحليل
بعد أن نتعرف على فكرة البرنامج ، نحتاج إلى تحليلها: اكتشف بعض الحقائق التي تسمح لك بتحويل البرنامج دون تغيير سلوكه. تعتمد العديد من التحسينات التي تمت مناقشتها أعلاه على تحليل البرنامج:
- طي ثابت: هل نتيجة التعبير تعمل قيمة ثابتة معروفة؟ هل حساب التعبير نقي؟
- نوع الصب والمضمنة: هل طريقة استدعاء نوع نوع مع تنفيذ واحد للطريقة تسمى؟
- : ?
- : «»? - ? ?
- : , ?
, , , . , , , .
, , , — , . .
(Inference Lattice)
, . , «» - :
Integer ? String ? Array[Float] ? PrintLogger ?
CharSequence ? String , - StringBuilder ?
Any , , ?
:

: ,
"hello" String ,
String CharSequence .
"hello" , (Singleton Type) — . :

, , . , . , , ,
String StringBuilder , , :
CharSequence . ,
0 ,
1 ,
2 , ,
Integer .

, , :

, , . , .
count
main :
static int main(int n){ int count = 0, multiplied = 0; while(count < n){ if (multiplied < 100) logger.log(count); count += 1; multiplied *= count; } return ...; }
ackermann ,
count ,
multiplied logger . :

,
count 0 block0 .
block1 , ,
count < n : ,
block3 return ,
block2 ,
count 1 count ,
block1 . ,
< false ,
block3 .
?
block0 . , count = 0.
block1 , , n ( , Integer ), , if . block2 block3.block3 , , block1b , block2 , , block1c . , block2 count , 1 count.- ,
count 0 1 : count Integer. - :
block1 n count Integer .
block2 , count Integer + 1 -> Integer . , count Integer , .
multiplied
,
multiplied :
block0 . , multiplied 0.
block1 , , . block2 block3 ( ).
block2 , block2 ( 0 ) count ( Integer ). 0 * Integer -> 0 , multiplied 0.
block1 block2 . multiplied 0 , .
multiplied 0 , , :
multiplied < 100 true.
if (multiplied < 100) logger.log(count); logger.log(count) .
- ,
multiplied , , 0 .
:

:

:
static int main(int n){ int count = 0; while(count < n){ logger.log(count); count += 1; } return ...; }
, , , , .
multiplied -> 0 , , . , , . , .
, . :
count ,
multiplied . ,
multiplied count ,
count multiplied . , .
, — : , . , ( ) . .
while , ,
O( ) . (, ) , , .
, .
, . , , , , .
. :
static int main(int n){ return called(n, 0); } static int called(int x, int y){ return x * y; }
:

main :
main(n)
called(n, 0)
called(n, 0) 0
main(n) 0
, , . .
,
called(n, 0) 0 , :

:
static int main(int n){ return 0; }
: A B, C, D, D C, B, D A. A B B A, A A, , !
, Java:
public static Any factorial(int n) { if (n == 1) { return 1; } else { return n * factorial(n - 1); } }
n int ,
Any : . ,
factorial int (
Integer ).
factorial ,
factorial factorial , ! ?
Bottom
Bottom :

« , , ».
Bottom factorial :

block0 . n Integer , 1 1 , n == 1 , true false .
true : return 1 .
false n - 1 n Integer .
factorial — , Bottom .
* n: Integer factorial : Bottom Bottom .
return Bottom .factorial 1 Bottom , 1 .
1 factorial , Bottom .
Integer * 1 Integer .
return Integer .factorial Integer 1 , Integer .
factorial , Integer . * n: Integer factorial: Integer , Integer , .
factorial Integer , , .
, .
Bottom , , .
* :
(n: Integer) * (factorial: Bottom)
(n: Integer) * (factorial: 1)
(n: Integer) * (factorial: Integer)
multiplied ,
O( ) . , , .
— , « ». , (« »), , (« »). .
main :
static int main(int n){ int count = 0, total = 0, multiplied = 0; while(count < n){ if (multiplied > 100) count += 1; count += 1; multiplied *= 2; total += 1; } return count; }
,
if (multiplied > 100) multiplied *= count multiplied *= 2 . .
, :
multiplied > 100 true , count += 1 («»).
total , («»).
, :
static int main(int n){ int count = 0; while(count < n){ count += 1; } return count; }
, .
:

, , :
block0 ,
block1 , ,
block1b , ,
block1c , ,
return block3 .
,
multiplied -> 0 , :

:

,
block1b (
0 > 100 )
true .
false block1c (
if ):
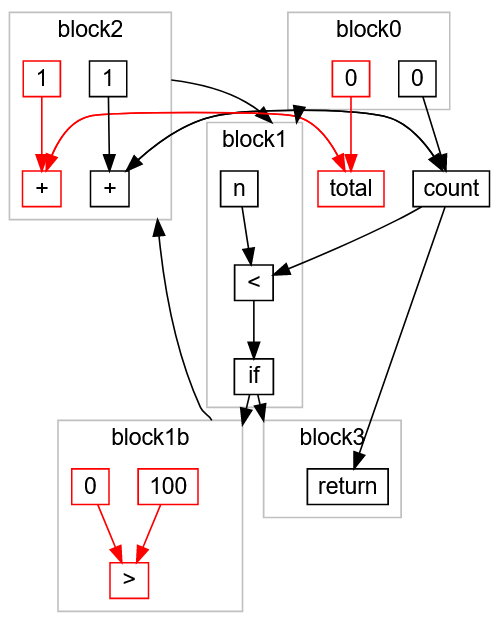
, « »
total > , - , , . ,
return ,
:
> ,
100 ,
0 block1b ,
total ,
0 ,
+ 1 ,
total block0 block2 . :

«» :
static int main(int n){ int count = 0; while(count < n){ count += 1; } return count; }
استنتاج
:
- -.
- , .
- , . .
- : «» «» , , .
- : , .
- , .
, , .
, . . , :