أواصل نشر محاضراتي ، التي كانت في الأصل مخصصة للطلاب الذين يدرسون في تخصص "الجيولوجيا الرقمية". هذا هو المنشور الثالث من الدورة في المحور ، المادة الأولى كانت تمهيدية ، لا يشترط قراءتها. ومع ذلك ، لفهم هذه المقالة ، من الضروري قراءة المقدمة إلى أنظمة المعادلات الخطية حتى لو كنت تعرف ما هي ، لأنني سأشير كثيرًا إلى أمثلة من هذه المقدمة.

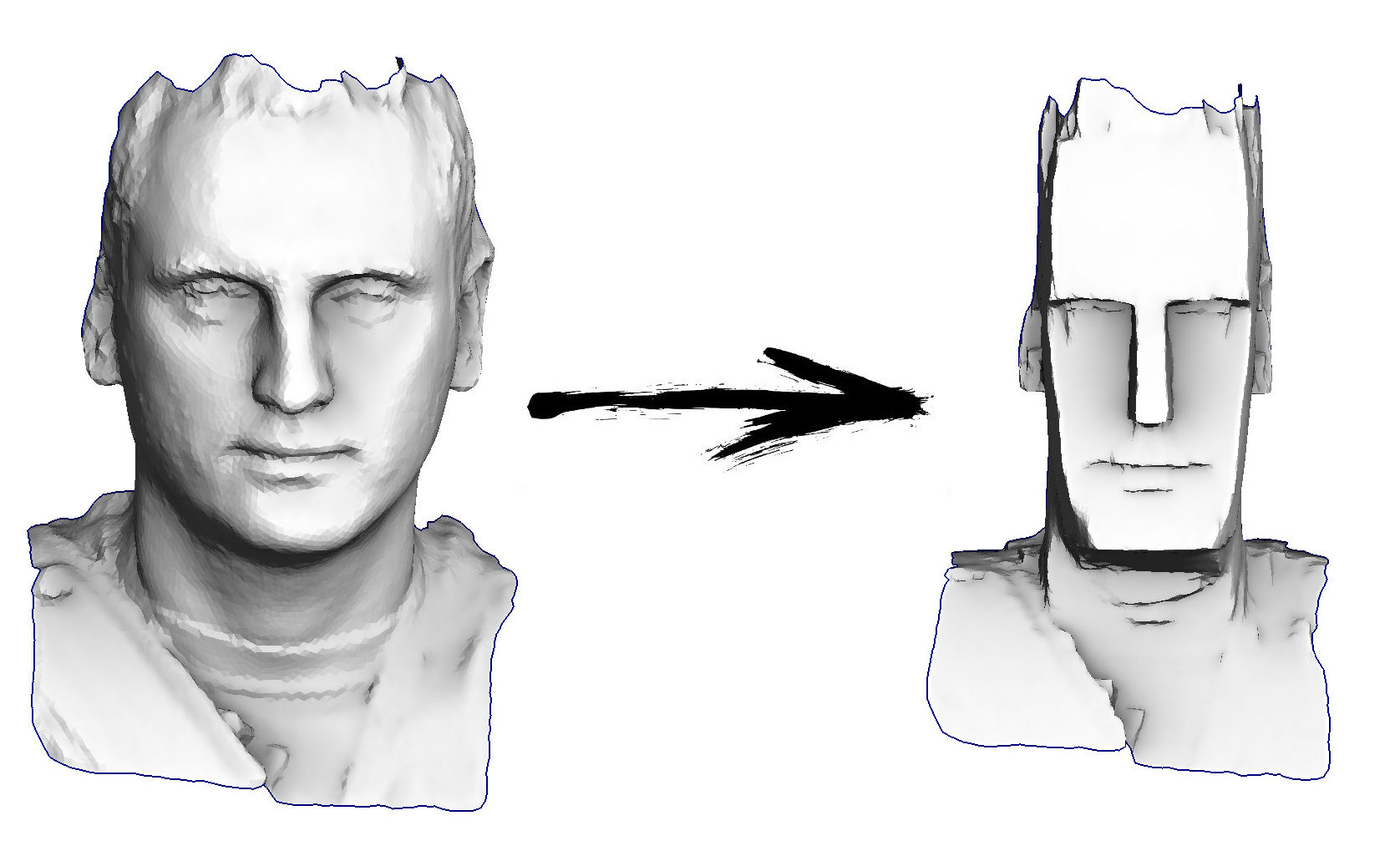
لذلك ، فإن مهمة اليوم: لمعرفة أبسط معالجة هندسية ، على سبيل المثال ، لتكون قادرة على تحويل رأسي إلى المعبود من جزيرة إيستر:



خطة المحاضرة الحالية:

• برنامج تعليمي حول نظرية الاحتمالات (مقالة تمهيدية ، اختياري)
  
• مقدمة في النظم الخطية للمعادلات
  
• التقليل من الأشكال التربيعية وأمثلة لمشاكل OLS
  
• من المربعات الصغرى إلى الشبكات العصبية
  

مستودع بالطبع الرسمي يعيش هنا . الكتاب لم ينته بعد ، وأنا بصدد تجميع المقالات المنشورة على حبري.

في هذه المقالة ، ستكون أداتي الرئيسية هي إيجاد الحد الأدنى من الوظائف التربيعية ؛ ولكن قبل أن نبدأ في استخدام هذه الأداة ، يجب أن تفهم على الأقل مكان وجود زر التشغيل / الإيقاف. أولاً ، قم بتحديث الذاكرة وتذكر المصفوفات وما هي الأرقام الموجبة وأيضًا ما هو المشتق.

المصفوفات والأرقام

في هذا النص ، سأستخدم بكثرة تدوين المصفوفة ، لذلك دعونا نتذكر ما هو عليه. لا تنظر إلى أبعد من ذلك في النص ، وتوقف مؤقتًا لبضع ثوان ، وحاول صياغة ماهية المصفوفة.

تفسيرات مصفوفة مختلفة

الجواب بسيط جدا. المصفوفة هي مجرد خزانة يتم تخزين الفجل فيها. كل شيت يقع في زنزانته ، يتم تجميع الخلايا في صفوف في صفوف وأعمدة. في حالتنا الخاصة ، الأرقام الحقيقية المعتادة هي حماقة. من الأسهل بالنسبة للمبرمج تقديم مصفوفة $$$دولا$ مثل شيء ما

float A[m][n]; 

لماذا هذه المخازن اللازمة؟ ماذا يصفون؟ ربما أزعجك ، لكن المصفوفة نفسها لا تصف أي شيء ، فهي تخزنه. على سبيل المثال ، في ذلك يمكنك تخزين معاملات أي وظائف. دعونا ننسى المصفوفات لثانية واحدة ، وتخيل أن لدينا عددًا $$$دولا$ . ماذا يعني ذلك؟ نعم ، يعرف الشيطان ... على سبيل المثال ، قد يكون معاملًا داخل دالة تأخذ رقمًا واحدًا كمدخلات وتعطي رقمًا آخر كإخراج:

$$

$$f (x): \ mathbb R \ rightarrow \ mathbb R$$

عالم الرياضيات يمكن أن يكتب نسخة واحدة من هذه الوظيفة كما

$$

$$f (x) = الفأس$$

حسنًا ، في عالم المبرمجين ، سيبدو كما يلي:

 float f(float x) { return a*x; } 

من ناحية أخرى ، لماذا هذه الوظيفة ، وليس وظيفة أخرى؟ لنأخذ واحدة أخرى!

$$

$$f (x) = ax ^ 2$$

منذ أن بدأت حول المبرمجين ، يجب أن أكتب رمزها :)

 float f(float x) { return x*a*x; } 

إحدى هذه الوظائف خطية ، والثانية تربيعية. أي واحد هو الصحيح؟ لا ، الرقم نفسه $$$دولا$ لا يحددها ، إنه يخزن بعض القيمة فقط! ما وظيفة تحتاج ، بناء واحدة من هذا القبيل.

يحدث الشيء نفسه مع المصفوفات ، فهذه مخازن ضرورية في حالة عدم وجود أرقام مفردة كافية (عدد قياسي) ، وهو نوع من التوسع في الأرقام. فوق المصفوفات ، تمامًا مثل الأرقام ، يتم تحديد عمليات الجمع والضرب.

دعونا نتخيل أن لدينا مصفوفة $$$دولا$ على سبيل المثال ، الحجم 2 × 2:

$$

$$A = \ تبدأ {bmatrix} a_ {11} & a_ {12} \\ a_ {21} & a_ {22} \ end {bmatrix}$$

هذه المصفوفة في حد ذاتها لا تعني شيئًا ، على سبيل المثال ، يمكن تفسيرها كدالة

$$

$$f (x): \ mathbb R ^ 2 \ rightarrow \ mathbb R ^ 2 ، \ quad f (x) = Ax$$

 vector<float> f(vector<float> x) { return vector<float>{a11*x[0] + a12*x[1], a21*x[0] + a22*x[1]}; } 

تحول هذه الوظيفة متجهًا ثنائي الأبعاد إلى متجه ثنائي الأبعاد. من الناحية الرسومية ، من المريح تقديم هذا كتحويل للصورة: نعطي الصورة للإدخال ، وعند الإخراج نحصل على نسخة مطولة و / أو مستديرة (ربما حتى معكوسة!). قريباً جداً ، سأقدم صورة مع أمثلة مختلفة على مثل هذا التفسير للمصفوفات.

ويمكن المصفوفة $$$دولا$ تخيل كدالة تحول متجهًا ثنائي الأبعاد إلى عددية:

$$

$$f (x): \ mathbb R ^ 2 \ rightarrow \ mathbb R ، \ quad f (x) = x ^ \ top A x = \ sum \ limit_i \ sum \ limit_j a_ {ij} x_i x_j$$

لاحظ أنه لا يتم تعريف الأس بشكل كبير مع المتجهات ، لذلك لا يمكنني الكتابة $$$x ^ 2$ كما كتب في حالة الأعداد العادية. أوصي بشدة لأولئك الذين لا يعتادون على التوفيق بسهولة بين مضاعفات المصفوفة ، وأذكر مرة أخرى قاعدة الضرب بالمصفوفة ، وتحقق من أن التعبير $$$x ^ \ top A x$ يسمح عموما ويعطي حقا العددية في الخروج. للقيام بذلك ، على سبيل المثال ، يمكنك وضع الأقواس بشكل صريح $$$x ^ \ top A x = (x ^ \ top A) x$ . أنا أذكرك أن لدينا $$$x$ هو متجه البعد 2 (المخزن في مصفوفة البعد 2x1) ، نكتب بوضوح جميع الأبعاد:

$$

$$\ underbrace {\ underbrace {\ left (\ underbrace {x ^ \ top} _ {1 \ times 2} \ times \ underbrace {A} _ {2 \ times 2} \ right)} _ {1 \ times 2} \ times \ underbrace {x} _ {2 \ times 1}} _ {1 \ times 1}$$

بالعودة إلى العالم الدافئ والرقيق للمبرمجين ، يمكننا كتابة نفس الوظيفة التربيعية بشيء من هذا القبيل:

 float f(vector<float> x) { return x[0]*a11*x[0] + x[0]*a12*x[1] + x[1]*a21*x[0] + x[1]*a22*x[1]; } 

ما هو الرقم الموجب؟

سأطرح الآن سؤالًا غبيًا جدًا: ما هو الرقم الإيجابي؟ لدينا أداة رائعة تسمى المسند بعد الآن $$$>$ . لكن خذ وقتك للإجابة على هذا الرقم $$$دولا$ إيجابية إذا وفقط إذا $$$a> 0$ سيكون ذلك سهلاً للغاية. دعونا نحدد الإيجابية على النحو التالي:

التعريف 1

عدد $$$دولا$ إيجابية إذا وفقط إذا كان للجميع غير الصفر الحقيقي $$$x \ in \ mathbb R ، \ x \ neq 0$ الشرط راض $$ .

تبدو صعبة للغاية ، ولكنها تنطبق بشكل مثالي على المصفوفات:

التعريف 2

مصفوفة مربعة $$$دولا$ يسمى إيجابي إيجابي إذا ، لأي صفر $$$x$ الشرط راض $$$x ^ \ top A x> 0$ بمعنى أن الشكل التربيعي المطابق موجب تمامًا في كل مكان باستثناء الأصل.

لماذا أحتاج إيجابية؟ كما ذكرت في بداية المقال ، ستكون أداتي الرئيسية هي البحث عن الحد الأدنى للوظائف التربيعية. ولكن من أجل البحث على الأقل ، لن يكون الأمر سيئًا إذا كان موجودًا! على سبيل المثال ، وظيفة $$$f (x) = - x ^ 2$ من الواضح أن الحد الأدنى غير موجود ، لأن الرقم -1 غير إيجابي ، و $$$f (x)$ ينخفض ​​إلى ما لا نهاية مع النمو $$$x$ : فروع المكافئ $$$f (x)$ أنظر للأسفل. المصفوفات المحددة الإيجابية جيدة في أن الأشكال التربيعية المقابلة تشكل مكافئًا له حد (فريد). يوضح الرسم التوضيحي التالي سبعة أمثلة مختلفة للمصفوفات. $$ ، سواء أكيدة إيجابية ومتماثلة ، وليس كذلك. الصف العلوي: تفسير المصفوفات كوظائف $$$f (x): \ mathbb R ^ 2 \ rightarrow \ mathbb R ^ 2$ . الصف الأوسط: تفسير المصفوفات كوظائف $$$f (x): \ mathbb R ^ 2 \ rightarrow \ mathbb R$ .



وبالتالي ، سوف أعمل مع مصفوفات محددة إيجابية ، والتي هي تعميم الأعداد الموجبة. علاوة على ذلك ، على وجه التحديد في حالتي ، ستكون المصفوفات أيضًا متناظرة! من الغريب أنه في كثير من الأحيان عندما يتحدث الناس عن اليقين الإيجابي ، فإنهم يقصدون أيضًا التماثل ، والذي يمكن تفسيره بشكل غير مباشر من خلال الملاحظة التالية (اختياري لفهم النص اللاحق).

الانحدار الغنائي على تماثل مصفوفات الأشكال التربيعية

لنلقِ نظرة على الشكل التربيعي $$$x ^ \ top M x$ لمصفوفة تعسفية $$$M$ . ثم إلى $$$M$ إضافة وطرح على الفور نصف نسخته المنقولة:

$$

$$M = \ underbrace {\ frac {1} {2} (M + M ^ \ top)} _ {: = M_s} + \ underbrace {\ frac {1} {2} (MM ^ \ top)} _ { : = M_a} = M_s + M_a$$

قالب $$$M_s$ متماثل: $$$M_s ^ \ top = M_s$ . قالب $$$M_a$ antisymmetric: $$$M_a ^ \ top = -M_a$ . هناك حقيقة رائعة وهي أنه بالنسبة لأي مصفوفة غير متماثلة ، فإن الشكل التربيعي المقابل يساوي الصفر. هذا يتبع من الملاحظة التالية:

$$

$$q = x ^ \ top M_a x = (x ^ \ top M_a ^ \ top x) ^ \ top = - (x ^ \ top M_a x) ^ \ top = -q$$

وهذا هو ، من الدرجة الثانية $$$x ^ \ top M_a x$ متساوية في وقت واحد $$$ف دولا$ و $$$-q$ ، وهذا ممكن فقط عندما $$$q \ equiv 0$ . من هذه الحقيقة يتبع ذلك لمصفوفة تعسفية $$$M$ شكل التربيعية المقابلة $$$x ^ \ top M x$ يمكن التعبير عنها من خلال مصفوفة متماثلة $$$M_s$ :

$$

$$x ^ \ top M x = x ^ \ top (M_s + M_a) x = x ^ \ top M_s x + x ^ \ top M_a x = x ^ \ top M_s x.$$

نحن نبحث عن الحد الأدنى من وظيفة من الدرجة الثانية

دعونا نعود لفترة وجيزة إلى العالم أحادي البعد ؛ أريد أن أجد الحد الأدنى من الوظيفة $$$f (x) = الفأس ^ 2 - 2bx$ . عدد $$$دولا$ بشكل إيجابي ، لذلك يوجد حد أدنى ؛ للعثور عليه ، فإننا نعادل الصفر المشتق المقابل: $$$\ frac {d} {dx} f (x) = 0$ . التفريق بين وظيفة أحادية اللون من العمل ليست: $$$\ frac {d} {dx} f (x) = 2ax - 2b = 0$ . لذلك تتلخص مشكلتنا في حل المعادلة $$$الفأس = 0 دولا$ ، حيث ، من خلال الجهود الرهيبة ، نحصل على حل $$$x ^ * = b / a$ . يوضح الشكل التالي معادلة مشكلتين: الحل $$$x ^ *$ معادلة $$$الفأس = 0 دولا$ يتزامن مع حل المعادلة $$$\ mathrm {argmin} _x (ax ^ 2 - 2bx)$ .



أنا أميل إلى حقيقة أن هدفنا العالمي هو تقليل الوظائف التربيعية ، لكننا نتحدث عن المربعات الصغرى. ولكن في الوقت نفسه ، ما نعرفه جيدًا هو كيفية حل المعادلات الخطية (وأنظمة المعادلات الخطية). إنه لأمر رائع أن يكون أحدهما معادلاً للآخر!

الشيء الوحيد المتبقي لنا هو التأكد من أن هذا التكافؤ في العالم أحادي البعد يمتد إلى الحالة $$$ن$ المتغيرات. للتحقق من ذلك ، نثبت أولاً ثلاث نظريات.

ثلاث نظريات ، أو التمييز بين تعبيرات المصفوفة

تقول النظرية الأولى أن المصفوفات $$$1 \ مرة 1 دولا$ المتغيرات فيما يتعلق بالتحول:

نظرية 1

$$$x \ in \ mathbb R \ Rightarrow x ^ \ top = x$

الدليل معقد للغاية لدرجة أنني يجب أن أغفله عن الإيجاز ، لكن حاول أن تجده بنفسك.

النظرية الثانية تسمح لنا بالتمييز بين الوظائف الخطية. في حالة وجود دالة حقيقية لمتغير واحد ، فإننا نعرف ذلك $$$\ frac {d} {dx} (bx) = b$ ولكن ما يحدث في حالة وظيفة حقيقية $$$ن$ المتغيرات؟

نظرية 2

$$$\ nabla b ^ \ top x = \ nabla x ^ \ top b = b$

هذا هو ، لا مفاجآت ، مجرد تسجيل مصفوفة لنفس النتيجة المدرسة. البرهان واضح ومباشر ، فقط اكتب تعريف التدرج:

$$

$$\ nabla (b ^ \ top x) = \ تبدأ {bmatrix} \ frac {\ جزئي (b ^ \ top x)} {\ جزئية x_1} \\ \ vdots \\ \ frac {\ جزئية (b ^ \ top x)} {\ جزئية x_n} \ end {bmatrix} = \ تبدأ {bmatrix} \ frac {\ جزئي (b_1 x_1 + \ dots + b_n x_n)} {\ جزئية x_1} \\ \ vdots \\ \ frac {\ جزئية (b_1 x_1 + \ dots + b_n x_n)} {\ جزئية x_n} \ end {bmatrix} = \ تبدأ {bmatrix} b_1 \\ \ vdots \\ b_n \ end {bmatrix} = b$$

تطبيق النظرية الأولى $$$b ^ \ top x = x ^ \ top b$ ، نكمل الدليل.

الآن نمر إلى الأشكال التربيعية. نحن نعلم أنه في حالة وجود دالة حقيقية لمتغير واحد $$$\ frac {d} {dx} (ax ^ 2) = 2ax$ وماذا سيحدث في حالة الشكل التربيعي؟

نظرية 3

$$$\ nabla (x ^ \ top A x) = (A + A ^ \ top) x$

بالمناسبة ، لاحظ أنه إذا كانت المصفوفة $$$دولا$ متماثل ، ثم تقول نظرية ذلك $$$\ nabla (x ^ \ top A x) = 2Ax$ .

هذا الدليل واضح ومباشر ، ما عليك سوى كتابة النموذج التربيعي كمجموع مزدوج:

$$

$$x ^ \ top A x = \ sum \ limit_i \ sum \ limit_j a_ {ij} x_i x_j$$

ثم لنرى ما هو المشتق الجزئي لهذا المبلغ المزدوج فيما يتعلق بالمتغير $$$x_i$ :
\ تبدأ {align *}
\ frac {\ جزئية (x ^ \ top A x)} {\ جزئية x_i}
& = \ frac {\ جزئية} {\ جزئية x_i} \ left (\ sum \ limit_ {k_1} \ sum \ limit_ {k_2} a_ {k_1 k_2} x_ {k_1} x_ {k_2} \ right) = \\
& = \ frac {\ جزئية} {\ جزئية x_i} \ left (
\ underbrace {\ sum \ limit_ {k_1 \ neq i} \ sum \ limit_ {k_2 \ neq i} a_ {ik_2} x_ {k_1} x_ {k_2}} _ {k_1 \ neq i، k_2 \ neq i} + \ underbrace {\ sum \ limit_ {k_2 \ neq i} a_ {ik_2} x_i x_ {k_2}} _ {k_1 = i، k_2 \ neq i} +
\ underbrace {\ sum \ limit_ {k_1 \ neq i} a_ {k_1 i} x_ {k_1} x_i} _ {k_1 \ neq i، k_2 = i} +
\ underbrace {a_ {ii} x_i ^ 2} _ {k_1 = i، k_2 = i} \ right) = \\
& = \ sum \ limit_ {k_2 \ neq i} a_ {ik_2} x_ {k_2} + \ sum \ limit_ {k_1 \ neq i} a_ {k_1 i} x_ {k_1} + 2 a_ {ii} x_i = \\
& = \ sum \ limit_ {k_2} a_ {ik_2} x_ {k_2} + \ sum \ limit_ {k_1} a_ {k_1 i} x_ {k_1} = \\
& = \ sum \ limit_ {j} (a_ {ij} + a_ {ji}) x_j \\
\ end {align *}
لقد كسرت المبلغ المزدوج إلى أربع حالات ، والتي أبرزتها الأقواس. كل من هذه الحالات الأربع يميز بشكل تافه. يبقى أن نفعل الإجراء الأخير ، وجمع المشتقات الجزئية في ناقل التدرج:

$$

$$\ nabla (x ^ \ top A x) = \ تبدأ {bmatrix} \ frac {\ جزئي (x ^ \ top ax)) {\ الجزئي x_1} \\ \ vdots \\ \ frac {\ جزئي (x ^ \ أعلى A x)} {\ جزئية x_n} \ end {bmatrix} = \ تبدأ {bmatrix} \ sum \ limit_ {j} (a_ {1j} + a_ {j1}) x_j \\ \ vdots \\ \ sum \ limit_ {j} (a_ {nj} + a_ {jn}) x_j \ end {bmatrix} = (A + A ^ \ top) x$$

الحد الأدنى للوظيفة التربيعية وحل النظام الخطي

دعونا لا ننسى اتجاه السفر. رأينا ذلك برقم موجب $$$دولا$ في حالة وجود وظائف حقيقية لمتغير واحد ، حل المعادلة $$ أو تقليل وظيفة التربيعية $$$\ mathrm {argmin} _x (ax ^ 2 - 2bx)$ هي واحدة ونفس الشيء.

نريد أن نظهر الاتصال المقابل في حالة مصفوفة محددة إيجابية متماثل $$$دولا$ .
لذلك نحن نريد أن نجد الحد الأدنى من وظيفة من الدرجة الثانية

$$

$$\ mathrm {argmin} _ {x \ in \ mathbb R ^ n} (x ^ \ top A x - 2b ^ \ top x).$$

بالضبط كما هو الحال في المدرسة ، نحن نساوي المشتق بصفر:

$$

$$\ nabla (x ^ \ top A x - 2b ^ \ top x) = \ start {bmatrix} 0 \\ \ vdots \\ 0 \ end {bmatrix}.$$

عامل التشغيل Hamilton خطي ، حتى نتمكن من إعادة كتابة المعادلة الخاصة بنا بالشكل التالي:

$$

$$\ nabla (x ^ \ top A x) - 2 \ nabla (b ^ \ top x) = \ تبدأ {bmatrix} 0 \\ \ vdots \\ 0 \ end {bmatrix}$$

الآن نطبق نظريتي التمايز الثانية والثالثة:

$$

$$(A + A ^ \ top) x - 2b = \ start {bmatrix} 0 \\ \ vdots \\ 0 \ end {bmatrix}$$

أذكر ذلك $$$دولا$ متماثل ، وقسم المعادلة إلى قسمين ، نحصل على نظام المعادلات الخطية التي نحتاجها:

$$

الصيحة ، بالانتقال من متغير واحد إلى كثير ، لم نفقد أي شيء على الإطلاق ، ويمكننا تقليل الوظائف التربيعية بشكل فعال!

نمر إلى المربعات الصغرى

أخيرًا ، يمكننا الانتقال إلى المحتوى الرئيسي لهذه المحاضرة. تخيل أن لدينا نقطتين على متن طائرة $$$(x_1 ، y_1)$ و $$$(x_2 ، y_2)$ ، ونريد أن نجد معادلة الخط المار بهاتين النقطتين. يمكن كتابة معادلة الخط كـ $$$y = \ alpha x + \ beta$ ، وهذا هو ، مهمتنا هي العثور على المعاملات $$$\ alpha$ و $$$\ beta$ . هذا التمرين للصف السابع من المدرسة ، نكتب نظام المعادلات:

$$

$$\ left \ {\ start {split} \ alpha x_1 + \ beta & = y_1 \\ \ alpha x_2 + \ beta & = y_2 \\ \ end {split} \ right.$$

لدينا معادلتين مع مجهولين ( $$$\ alpha$ و $$$\ beta$ ) ، الباقي معروف.

في الحالة العامة ، يوجد حل وهو فريد من نوعه. للراحة ، نعيد كتابة نفس النظام في شكل مصفوفة:

$$

$$\ underbrace {\ start {bmatrix} x_1 & 1 \\ x_2 & 1 \ end {bmatrix}} _ {: = A} \ underbrace {\ start {bmatrix} \ alpha \\ \ beta \ end {bmatrix}} _ {: = x} = \ underbrace {\ start {bmatrix} y_1 \\ y_2 \ end {bmatrix}} _ {: = b}$$

نحصل على معادلة النوع $$ وهو حل تافه $$$x ^ * = A ^ {- 1} b$ .

الآن تخيل أن لدينا ثلاث نقاط نحتاج من خلالها إلى رسم خط مستقيم:

$$

$$\ left \ {\ start {split} \ alpha x_1 + \ beta & = y_1 \\ \ alpha x_2 + \ beta & = y_2 \\ \ alpha x_3 + \ beta & = y_3 \\ \ end {split} \ right .$$

في شكل مصفوفة ، يتم كتابة هذا النظام على النحو التالي:

$$

$$\ underbrace {\ start {bmatrix} x_1 & 1 \\ x_2 & 1 \\ x_3 & 1 \ end {bmatrix}} _ {: = A \، (3 \ times 2)} \ underbrace {\ start {bmatrix} \ alpha \\ \ beta \ end {bmatrix}} _ {: = x \، (2 \ times 1)} = \ underbrace {\ start {bmatrix} y_1 \\ y_2 \\ y_3 \ end {bmatrix}} _ { : = b \، (3 \ times 1)}$$

الآن لدينا مصفوفة $$$دولا$ مستطيلة ، وببساطة لا وجود عكس! هذا أمر طبيعي تمامًا ، نظرًا لأن لدينا متغيرين وثلاثة معادلات فقط ، وفي الحالة العامة ، لا يوجد لهذا النظام أي حل. هذا وضع طبيعي تمامًا في العالم الحقيقي ، عندما تكون النقاط عبارة عن بيانات من القياسات الصاخبة ، ونحن بحاجة إلى العثور على المعلمات $$$\ alpha$ و $$$\ beta$ أن أفضل بيانات القياس التقريبي . لقد درسنا بالفعل هذا المثال في المحاضرة الأولى ، عند معايرة الفولاذ. ولكن بعد ذلك كان حلنا جبريًا صعبًا ومرهقًا للغاية. دعونا نحاول بطريقة أكثر سهولة.

يمكن كتابة نظامنا على النحو التالي:

$$

$$\ alpha \ underbrace {\ start {bmatrix} x_1 \\ x_2 \\ x_3 \ end {bmatrix}} _ {: = \ vec {i}} + \ beta \ underbrace {\ start {bmatrix} 1 \\ 1 \ \ 1 \ end {bmatrix}} _ {: = \ vec {j}} = \ تبدأ {bmatrix} y_1 \\ y_2 \\ y_3 \ end {bmatrix}$$

أو باختصار ،

$$

$$\ alpha \ vec {i} + \ beta \ vec {j} = \ vec {b}.$$

ناقلات $$$\ vec i$ . $$$\ vec j$ و $$$\ vec b$ معروف ، بحاجة إلى العثور على العددية $$$\ alpha$ و $$$\ beta$ .
مزيج خطي واضح $$$\ alpha \ vec {i} + \ beta \ vec {j}$ يولد طائرة ، وإذا كان ناقل $$$\ vec b$ لا تكمن في هذه الطائرة ، ثم لا يوجد حل دقيق ؛ ومع ذلك ، نحن نبحث عن حل تقريبي.

دعنا نعرّف خطأ القرار كـ $$$\ vec {e} (\ alpha، \ beta): = \ alpha \ vec {i} + \ beta \ vec {j} - \ vec b$ . هدفنا هو العثور على هذه القيم المعلمة $$$\ alpha$ و $$$\ beta$ التي تقلل من طول الناقل $$$\ vec {e} (\ alpha، \ beta)$ . بمعنى آخر ، المشكلة مكتوبة كـ $$$\ mathrm {argmin} _ {\ alpha، \ beta} \ | \ vec {e} (\ alpha، \ beta) \ |$ .
هنا هو التوضيح:.



بعد أن أعطى ناقلات $$$\ vec i$ . $$$\ vec j$ و $$$\ vec b$ ، نحاول تقليل طول ناقل الخطأ $$$\ vec e$ . من الواضح ، يتم تقليل طوله إلى الحد الأدنى إذا كان عموديًا على الطائرة الممتدة على النواقل $$$\ vec i$ و $$$\ vec j$ .

لكن مهلا ، أين هي المربعات الصغرى؟ الآن سوف يكونون. وظيفة استخراج الجذر $$$\ sqrt {\ cdot}$ رتابة لذلك $$$\ mathrm {argmin} _ {\ alpha، \ beta} \ | \ vec {e} (\ alpha، \ beta) \ |$ = $$$\ mathrm {argmin} _ {\ alpha، \ beta} \ | \ vec {e} (\ alpha، \ beta) \ | ^ 2$ !

من الواضح تمامًا أنه يتم تقليل طول متجه الخطأ إلى الحد الأدنى إذا كان عموديًا على المستوى الممتد فوق المتجهات. $$$\ vec i$ و $$$\ vec j$ ، والتي يمكن كتابتها عن طريق مساوي الصفر في المنتجات العددية المقابلة:

$$

$$\ left \ {\ start {split} \ vec {i} ^ \ top \ vec {e} (\ alpha، \ beta) & = 0 \\ \ vec {j} ^ \ top \ vec {e} (\ alpha ، \ beta) & = 0 \ end {split} \ right.$$

في شكل مصفوفة ، يمكن كتابة هذا النظام نفسه باسم

$$

$$\ تبدأ {bmatrix} x_1 & x_2 & x_3 \\ 1 & 1 & 1 \ end {bmatrix} \ left (\ alpha \ تبدأ {bmatrix} x_1 \\ x_2 \\ x_3 \ end {bmatrix} + + \ beta \ start {bmatrix} 1 \\ 1 \\ 1 \ end {bmatrix} - \ start {bmatrix} y_1 \\ y_2 \\ y_3 \ end {bmatrix} \ right) = \ تبدأ {bmatrix} 0 \\ 0 \ end {bmatrix }$$

أو غير ذلك

$$

$$\ تبدأ {bmatrix} x_1 & x_2 & x_3 \\ 1 & 1 & 1 \ end {bmatrix} \ left (\ start {bmatrix} x_1 & 1 \\ x_2 & 1 \\ x_3 & 1 \ end {bmatrix} \ تبدأ {bmatrix} \ alpha \\ \ beta \ end {bmatrix} - \ تبدأ {bmatrix} y_1 \\ y_2 \\ y_3 \ end {bmatrix} \ right) = \ تبدأ {bmatrix} 0 \\ 0 \ end {bmatrix }$$

لكننا لن نتوقف عند هذا الحد ، حيث يمكن تقليص السجل:

$$

$$A ^ \ top (Ax - b) = \ start {bmatrix} 0 \\ 0 \ end {bmatrix}$$

وأحدث تحول:

$$

$$A ^ \ top ax = A ^ \ top b.$$

دعنا نحسب الأبعاد. قالب $$$دولا$ له حجم $$ ول $$$A ^ \ top A$ له حجم $$ . قالب $$$ب$ له حجم $$ لكن المتجه $$$A ^ \ top b$ له حجم $$$2 \ مرة 1 دولا$ . هذا هو ، في الحالة العامة ، المصفوفة $$$A ^ \ top A$ عكسها! وعلاوة على ذلك، $$$A ^ \ top A$ لديها اثنين من الخصائص لطيفة.

نظرية 4

$$$A ^ \ top A$ متماثل.

هذا ليس من الصعب على الإطلاق إظهار:

$$

$$(A ^ \ top A) ^ \ top = A ^ \ top (A ^ \ top) ^ \ top = A ^ \ top A.$$

نظرية 5

$$$A ^ \ top A$ إيجابيا شبه محدد: $$$\ forall x \ in \ mathbb R ^ n \ quad x ^ \ top A ^ \ top A x \ geq 0.$

هذا يتبع من حقيقة أن $$$x ^ \ top A ^ \ top A x = (A x) ^ \ top A x> 0$ .

وبالإضافة إلى ذلك، $$$A ^ \ top A$ محددة إيجابية إذا $$$دولا$ لديه أعمدة مستقلة خطيا (رتبة $$$دولا$ يساوي عدد المتغيرات في النظام).

إجمالاً ، بالنسبة لنظام مجهول الهوية ، أثبتنا أن التقليل إلى أدنى حد من وظيفة من الدرجة الثانية $$$\ mathrm {argmin} _ {\ alpha، \ beta} \ | \ vec {e} (\ alpha، \ beta) \ | ^ 2$ أي ما يعادل حل نظام المعادلات الخطية $$$A ^ \ top A x = A ^ \ top b$ . بالطبع ، ينطبق كل هذا المنطق على أي عدد آخر من المتغيرات ، ولكن دعنا نكتب كل شيء معًا بشكل مضغوط مرة أخرى مع حساب جبري بسيط. نبدأ بمشكلة المربعات الصغرى ، ونصل إلى الحد الأدنى من الوظيفة التربيعية للشكل المألوف ، ومن هنا نستنتج أنها تعادل حل نظام المعادلات الخطية. لذلك ، دعنا نذهب:

$$

$$\ تبدأ {split} \ mathrm {argmin} \ | الفأس - b \ | ^ 2 & = \ mathrm {argmin} (Ax-b) ^ \ top (Ax-b) = \\ & = \ mathrm {argmin} (x ^ \ top A ^ \ top - b ^ \ top) (Ax-b) = \\ & = \ mathrm {argmin} (x ^ \ top A ^ \ top A x - b ^ \ top Ax - x ^ \ top A ^ \ top b + \ underbrace {b ^ \ top b} _ {\ rm const}) = \\ & = \ mathrm {argmin} (x ^ \ top A ^ \ top A x - 2b ^ \ top Ax) = \\ & = \ mathrm {argmin} ( x ^ \ top \ underbrace {(A ^ \ top A)} _ {: = A '} x - 2 \ underbrace {(A ^ \ top b)} _ {: = b'} \ phantom {} ^ \ top x) \ end {split}$$

لذلك مشكلة المربعات الصغرى $$$\ mathrm {argmin} \ | الفأس - ب \ | ^ 2$ أي ما يعادل تقليل الوظيفة التربيعية $$$\ mathrm {argmin} (x ^ \ top A 'x - 2b' ^ \ top x)$ مع (في الحالة العامة) مصفوفة محددة إيجابية متماثل $$$A '$ والذي ، بدوره ، يعادل حل نظام المعادلات الخطية $$$A'x = b '$ . يا للعجب. انتهت النظرية.

دعنا ننتقل إلى الممارسة

مثال واحد ، واحد الأبعاد

دعنا نتذكر مثال واحد من مقال سابق :

 # initialize the data array x = [0.] * 32 x[0] = x[31] = 1. x[18] = 2. # smooth the array values other than at indices 0,18,31 for iter in range(1000): for i in range(len(x)): if i in [0,18,31]: continue x[i] = (x[i-1] + x[i+1])/2. 

لدينا مجموعة س العادية من 32 عنصرا ، تهيئة على النحو التالي:



ثم سننفذ الإجراء التالي ألف مرة: لكل خلية س [i] نكتب متوسط ​​قيمة الخلايا المجاورة فيه: x [i] = (x [i-1] + x [i + 1]) / 2. الاستثناء الوحيد: لن نقوم بإعادة كتابة عناصر المصفوفة بالأرقام 0 و 18 و 31. هكذا يبدو تطور المصفوفة في التكرار الأول والمائة والخمسين:



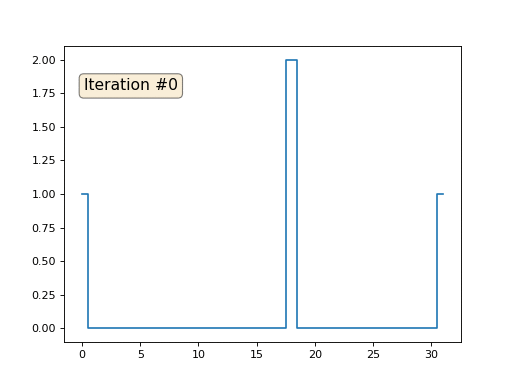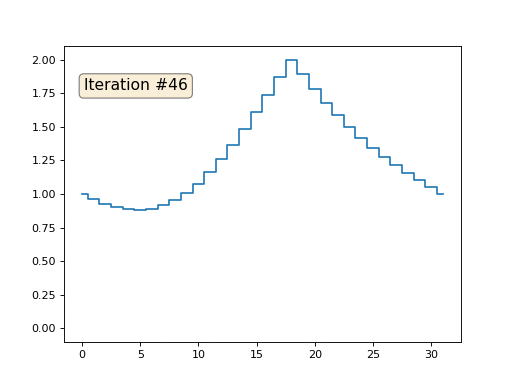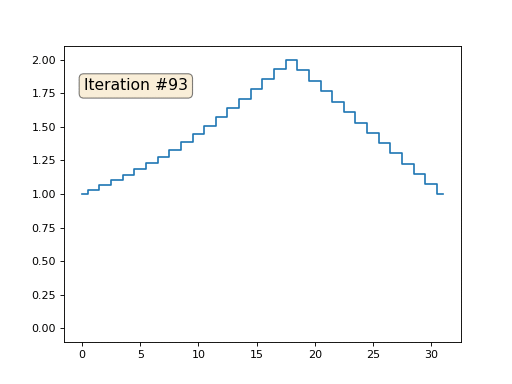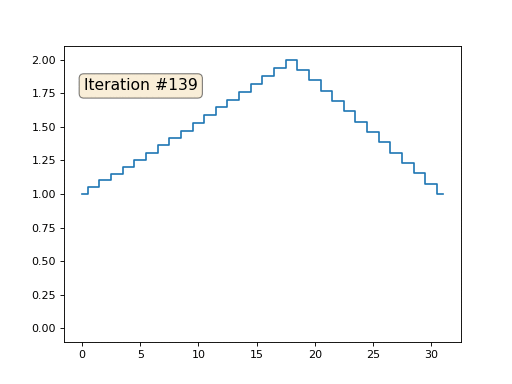
كما وجدنا في مقال سابق ، اتضح أن كود الشفرة الثعبانية المكون من أربعة أسطر يحل نظام المعادلات الخطية التالي باستخدام طريقة Gauss-Seidel:



لقد اكتشفوا ذلك ، لكن من أين أتى هذا النظام؟ أي نوع من السحر؟ دعنا نستطلع لمدة ثانية ، وحاول حل نظام مختلف قليلاً. لا يزال لدي 32 متغيرًا ، لكن الآن أريدهم جميعًا أن يكونوا متساوين مع بعضهم البعض. هذا ليس من الصعب تدوينه ، يكفي كتابة نظام من المعادلات ينص على أن جميع العناصر المجاورة متساوية في أزواج:



رمز Python أعلاه ، من حيث المبدأ ، لا يمس قيم المتغيرات الثلاثة: x0 ، x18 ، x31 ، لذلك دعنا ننقلها إلى الجانب الأيمن من نظام المعادلات ، أي نستبعد من مجموعة المجهولين:



أقوم بإصلاح القيمة الأولية x0 = 1 ، المعادلة الأولى تقول x1 = x0 = 1 ، والمعادلة الثانية تقول x2 = x1 = x0 = 1 وهكذا ، حتى نصل إلى المعادلة 1 = x0 = x17 = x18 = 2 أوه. لكن هذا النظام لا يوجد لديه حل: ((

ولا يهمني ، نحن المبرمجين! دعنا ندعو المربعات الصغرى للمساعدة! يمكن كتابة نظامنا غير القابل للحل في شكل مصفوفة $$ . لحل نظامنا تقريبًا ، يكفي لحل النظام $$$A^\top Ax=A^\top b$ .ثم اتضح أن هذا هو بالضبط نظام واحد في واحد من المعادلات من المادة السابقة!

بشكل حدسي ، يمكن للمرء أن يتخيل عملية إنشاء مصفوفة من النظام على النحو التالي: نحن نربط من خلال الينابيع القيم التي نريد تحقيق المساواة. على سبيل المثال ، في حالتنا ، نحن نريد$$$x_i$ كان على قدم المساواة $$$x_{i+1}$ ، لذلك نضيف المعادلة $$$x_i - x_{i+1}=0$معلقة بين هذه القيم ربيع من شأنها أن تسحبهم معا. ولكن نظرًا لأن قيم x0 و x18 و x31 ثابتة بإحكام ، فلم يتبق شيء للقيم المجانية سوى تمديد الينابيع بشكل متساوٍ ، مما ينتج عنه (في هذه الحالة) حل خطي متقطع.

دعنا نكتب برنامجًا يحل نظام المعادلات هذا. في المقالة الأخيرة ، رأينا أن طريقة Gauss-Seidel بسيطة جدًا في البرمجة ، لكن لديها تقارب بطيء جدًا ، لذلك سيكون من الأفضل استخدام حل حقيقي لأنظمة المعادلات الخطية. في أبسط الحالات ، على سبيل المثال ، لدينا مثال أحادي البعد ، قد يبدو الرمز كالتالي:

 import numpy as np n = 32 # size of the vector to produce # fill the matrix with 2nd order finite differences A = np.matrix(np.zeros((n-1, n))) for i in range(0,n-1): A[i, i] = -1. A[i, i+1] = 1. # eliminate the constrained variables from the matrix A = A[:,[*range(1,18)] + [*range(19,31)]] b = np.matrix(np.zeros((n-1, 1))) b[0,0] = 1. b[17,0] = -2. b[18,0] = 2. b[n-2,0] = -1. # solve the system x = np.linalg.inv(A.transpose()*A)*A.transpose()*b x = x.transpose().tolist()[0] # re-introduce the constrained variables x.insert(0, 1.) x.insert(18, 2.) x.append(1.) 

ينتج هذا الرمز قائمة × مكونة من 32 عنصرًا يتم تخزين الحل بها. نحن نبني مصفوفة$$$دولا$ بناء ناقلات $$$ب$ نحصل على ناقل مع الحل $$$x = (A^\top A)^{-1}A^\top b$ثم نقوم بإدخال قيمنا الثابتة x0 = 1 ، x18 = 2 و x31 = 1 في هذا المتجه.

يعمل هذا الكود بالعمل الضروري ، لكن من غير المريح نقل قيم المتغيرات الثابتة إلى الجانب الأيمن. هل من الممكن الغش؟ يمكنك! لنلقِ نظرة على الكود التالي:

 import numpy as np n = 32 # size of the vector to produce # fill the matrix with 2nd order finite differences A = np.matrix(np.zeros((n-1+3, n))) for i in range(0,n-1): A[i, i] = -1. A[i, i+1] = 1. # enforce the constraints through the quadratic penalty A[n-1+0, 0] = 100. A[n-1+1,18] = 100. A[n-1+2,31] = 100. b = np.matrix(np.zeros((n-1+3, 1))) b[n-1+0,0] = 100.*1. b[n-1+1,0] = 100.*2. b[n-1+2,0] = 100.*1. # solve the system x = np.linalg.inv(A.transpose()*A)*A.transpose()*b x = x.transpose().tolist()[0] 

من وجهة نظر المبرمج ، يكون هذا الجهاز جميلًا ، ويتم الحصول على المتجه x فورًا من البعد المطلوب ، ويتم ملء المصفوفات A و b بسهولة أكبر. ولكن ما هي الحيلة؟ دعنا نكتب نظام المعادلات التي نحلها:



انظر بعناية إلى المعادلات الثلاث الأخيرة:
100 x0 = 100 * 1
100 x18 = 100 * 2
100 x31 = 100 * 1

هل يمكن أن تكون أسهل في كتابتها كما يلي؟
x0 = 1
x18 = 2
x31 = 1

لا ، ليس أسهل. كما قلت من قبل ، فإن كل معادلة معلقة بالينابيع ، في هذه الحالة ، الربيع بين x0 والقيمة 1 ، والربيع بين x18 والقيمة 2 ، وأخيراً ، سيتم جذب المتغير x31 أيضًا إلى الوحدة.

لكن معامل 100 هناك لسبب ما. نتذكر أنه لا يمكن حل هذا النظام ، فنحن نحله بمعنى المربعات الصغرى ، مما يقلل من الوظيفة التربيعية المقابلة. بضرب 100 في كل من معاملات المعادلات الثلاث الأخيرة ، فإننا نقدم عقوبة لانحراف x0 و x18 و x32 عن القيم المطلوبة ، وعشرة آلاف مرة (100 ^ 2) تتجاوز عقوبة الانحراف عن المساواة$$$x_i = x_{i+1}$ .وبصورة تقريبية ، فإن الينابيع في المعادلات الثلاث الأخيرة أصعب بعشرة آلاف مرة من جميع المعادلات الأخرى. إن طريقة الجزاء التربيعية هذه هي أداة مريحة للغاية لإدخال القيود ؛ إنها أبسط بكثير (وإن لم يكن بدون عيوب) من تقليل مجموعة من المتغيرات.

المثال الثاني ، ثلاثي الأبعاد

دعنا ننتقل إلى شيء أكثر إثارة للاهتمام من تجانس عناصر مجموعة ذات بعد واحد! بادئ ذي بدء ، سنفعل الشيء نفسه تمامًا ، ولكن مع بيانات أكثر إثارة للاهتمام وأدوات حقيقية. أرغب في الحصول على سطح ثلاثي الأبعاد ، وإصلاح حدوده ، وتنعيم بقية السطح قدر الإمكان: يتوفر



الرمز هنا ، لكن في حال سأقدم لك قائمة كاملة بالملف الرئيسي:

 #include <vector> #include <iostream> #include "OpenNL_psm.h" #include "geometry.h" #include "model.h" int main(int argc, char** argv) { if (argc<2) { std::cerr << "Usage: " << argv[0] << " obj/model.obj" << std::endl; return 1; } Model m(argv[1]); for (int d=0; d<3; d++) { // solve for x, y and z separately nlNewContext(); nlSolverParameteri(NL_NB_VARIABLES, m.nverts()); nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE); nlBegin(NL_SYSTEM); nlBegin(NL_MATRIX); for (int i=0; i<m.nhalfedges(); i++) { // fix the boundary vertices if (m.opp(i)!=-1) continue; int v = m.from(i); nlRowScaling(100.); nlBegin(NL_ROW); nlCoefficient(v, 1); nlRightHandSide(m.point(v)[d]); nlEnd(NL_ROW); } for (int i=0; i<m.nhalfedges(); i++) { // smooth the interior if (m.opp(i)==-1) continue; int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(1.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlEnd(NL_ROW); } nlEnd(NL_MATRIX); nlEnd(NL_SYSTEM); nlSolve(); for (int i=0; i<m.nverts(); i++) { m.point(i)[d] = nlGetVariable(i); } } std::cout << m; return 0; } 

كتبت أبسط محلل لملفات .obj ذات واجهة الموجة ، لذلك يتم تحميل النموذج في سطر واحد. كحل حلال ، سأستخدم OpenNL ، وهو حل قوي للغاية لأقل مشاكل المربعات مع المصفوفات المتناثرة. يرجى ملاحظة أن أبعاد المصفوفات يمكن أن تكون هائلة: على سبيل المثال ، إذا أردنا الحصول على صورة بالأبيض والأسود بحجم 1000 × 1000 بكسل ، فإن المصفوفة$$$A^\top A$سيكون لدينا حجم مليون في المليون! ومع ذلك ، في الممارسة العملية ، غالبًا ما تكون الغالبية العظمى من عناصر هذه المصفوفة صفرية ، لذلك ليس كل شيء مخيفًا ، لكن لا تزال بحاجة إلى استخدام حل خاص.

لذلك دعونا ننظر إلى الكود. للبدء ، أعلن للحامل ما أريد القيام به:

  nlNewContext(); nlSolverParameteri(NL_NB_VARIABLES, m.nverts()); nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE); nlBegin(NL_SYSTEM); nlBegin(NL_MATRIX); 

أريد أن يكون لديك مصفوفة $$$A^\top A$حجم (عدد القمم) × (عدد القمم). الاهتمام ، ونحن نقدم حلالا مصفوفة$$$دولا$ و $$$A^\top A$سوف يبنيها بنفسه ، وهي مريحة للغاية! أيضا ، انتبه إلى حقيقة أنني لا أحل نظام واحد من المعادلات ، ولكن ثلاثة في سلسلة ل x و y و z (كذبت أن المشكلة هي ثلاثية الأبعاد ، لا تزال أحادية الأبعاد!)

ثم أعلن صف صف مصفوفة لدينا. للبدء ، أقوم بإصلاح القمم الموجودة على حافة السطح:

  for (int i=0; i<m.nhalfedges(); i++) { // fix the boundary vertices if (m.opp(i)!=-1) continue; int v = m.from(i); nlRowScaling(100.); nlBegin(NL_ROW); nlCoefficient(v, 1); nlRightHandSide(m.point(v)[d]); nlEnd(NL_ROW); } 

يمكنك أن ترى أنني أستخدم عقوبة مربعة قدرها 100 ^ 2 لإصلاح رؤوس الحواف.

حسنًا ، ثم لكل زوج من الرؤوس المجاورة أعلق ربيعًا من الصلابة 1 بينهما:

  for (int i=0; i<m.nhalfedges(); i++) { // smooth the interior if (m.opp(i)==-1) continue; int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(1.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlEnd(NL_ROW); } 

ننفذ الكود ونرى كيف تم سلاسة الوجه على سطح فيلم الصابون على سلك منحني. لقد حللنا للتو مشكلة ديريتشليت ، بعد أن حصلنا على مساحة من الحد الأدنى من المساحة.

نحن نعزز الخصائص

دعونا نحول وجهنا إلى قناع بشع:



في المقالة السابقة ، سبق لي أن أوضحت كيفية القيام بذلك على الركبة ، وهنا أعطي رمزًا حقيقيًا يستخدم أقل المربعات حلالًا:

  for (int d=0; d<3; d++) { // solve for x, y and z separately nlNewContext(); nlSolverParameteri(NL_NB_VARIABLES, m.nverts()); nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE); nlBegin(NL_SYSTEM); nlBegin(NL_MATRIX); for (int i=0; i<m.nhalfedges(); i++) { // fix the boundary vertices if (m.opp(i)!=-1) continue; int v = m.from(i); nlRowScaling(100.); nlBegin(NL_ROW); nlCoefficient(v, 1); nlRightHandSide(m.point(v)[d]); nlEnd(NL_ROW); } for (int i=0; i<m.nhalfedges(); i++) { // light attachment to the original geometry if (m.opp(i)==-1) continue; int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(.2); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlRightHandSide(m.point(v1)[d] - m.point(v2)[d]); nlEnd(NL_ROW); } for (int v=0; v<m.nverts(); v++) { // amplify the curvature nlRowScaling(1.); nlBegin(NL_ROW); int nneigh = m.incident_halfedges(v).size(); nlCoefficient(v, nneigh); Vec3f curvature = m.point(v)*nneigh; for (int hid : m.incident_halfedges(v)) { nlCoefficient(m.to(hid), -1); curvature = curvature - m.point(m.to(hid)); } nlRightHandSide(2.5*curvature[d]); nlEnd(NL_ROW); } nlEnd(NL_MATRIX); nlEnd(NL_SYSTEM); nlSolve(); for (int i=0; i<m.nverts(); i++) { m.point(i)[d] = nlGetVariable(i); } } 

الرمز الكامل متاح هنا . كيف يعمل؟ كما في المثال السابق ، أبدأ بتحديد رؤوس الحواف. بعد ذلك أقول لكل حافة I (بهدوء ، مع معامل 0.2) أنه سيكون من الرائع لو كان له نفس الشكل تمامًا كما في السطح الأصلي:

  for (int i=0; i<m.nhalfedges(); i++) { // light attachment to the original geometry if (m.opp(i)==-1) continue; int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(.2); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlRightHandSide(m.point(v1)[d] - m.point(v2)[d]); nlEnd(NL_ROW); } 

إذا لم تقم بأي شيء آخر وقمت بحل المشكلة كما هي ، فيجب أن نحصل بالضبط على ما كان عند الإخراج في الإخراج: حد المخرجات مساوٍ لحدود الإدخال ، بالإضافة إلى أن الاختلافات في الإخراج تساوي الاختلافات عند الإدخال.

لكننا لن نتوقف عند هذا الحد!

  for (int v=0; v<m.nverts(); v++) { // amplify the curvature nlRowScaling(1.); nlBegin(NL_ROW); int nneigh = m.incident_halfedges(v).size(); nlCoefficient(v, nneigh); Vec3f curvature = m.point(v)*nneigh; for (int hid : m.incident_halfedges(v)) { nlCoefficient(m.to(hid), -1); curvature = curvature - m.point(m.to(hid)); } nlRightHandSide(2.5*curvature[d]); nlEnd(NL_ROW); } 

أقوم بإضافة المزيد من المعادلات إلى نظامنا. بالنسبة لكل قمة ، أحسب انحناء السطح من حوله في سطح الإدخال ، واضربه مرتين ونصف ، أي يجب أن يكون لسطح الإخراج انحناء كبير في كل مكان.

ثم ندعو حلالا لدينا والحصول على كاريكاتور جيد.

المثال الأخير لهذا اليوم

حتى هذه اللحظة ، لم نر مثالًا واحدًا جديدًا ، فقد تم عرض كل شيء بالفعل في المقالة السابقة. دعونا نحاول القيام بشيء أقل تافهة من أبسط عملية تنعيم ، والتي يمكن الحصول عليها بسهولة دون استخدام أي محللين. الكود متوفر هنا ، لكن دعني أعطيك قائمة:

 #include <vector> #include <iostream> #include "OpenNL_psm.h" #include "geometry.h" #include "model.h" const Vec3f axes[] = {Vec3f(1,0,0), Vec3f(-1,0,0), Vec3f(0,1,0), Vec3f(0,-1,0), Vec3f(0,0,1), Vec3f(0,0,-1)}; int snap(Vec3f n) { // returns the coordinate axis closest to the given normal double nmin = -2.0; int imin = -1; for (int i=0; i<6; i++) { double t = n*axes[i]; if (t>nmin) { nmin = t; imin = i; } } return imin; } int main(int argc, char** argv) { if (argc<2) { std::cerr << "Usage: " << argv[0] << " obj/model.obj" << std::endl; return 1; } Model m(argv[1]); std::vector<int> nearest_axis(m.nfaces()); for (int i=0; i<m.nfaces(); i++) { Vec3f v[3]; for (int j=0; j<3; j++) v[j] = m.point(m.vert(i, j)); Vec3f n = cross(v[1]-v[0], v[2]-v[0]).normalize(); nearest_axis[i] = snap(n); } for (int d=0; d<3; d++) { // solve for x, y and z separately nlNewContext(); nlSolverParameteri(NL_NB_VARIABLES, m.nverts()); nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE); nlBegin(NL_SYSTEM); nlBegin(NL_MATRIX); for (int i=0; i<m.nhalfedges(); i++) { int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(1.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlRightHandSide(m.point(v1)[d] - m.point(v2)[d]); nlEnd(NL_ROW); int axis = nearest_axis[i/3]/2; if (d!=axis) continue; nlRowScaling(2.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlEnd(NL_ROW); } nlEnd(NL_MATRIX); nlEnd(NL_SYSTEM); nlSolve(); for (int i=0; i<m.nverts(); i++) { m.point(i)[d] = nlGetVariable(i); } } std::cout << m; return 0; } 

نحن لا نزال نعمل على نفس السطح كما كان من قبل. نحن ندعو وظيفة snap () لكل مثلث. تشير هذه الوظيفة إلى أي محور من نظام الإحداثيات هو الأقرب إلى المعدل الطبيعي لهذا المثلث. وهذا يعني أننا نريد أن نعرف أن هذا المثلث أكثر ميلًا رأسيًا أو أفقيًا. حسنًا ، نريد تغيير هندسة سطحنا حتى يصبح أقرب إلى الأفقي أقرب! يُظهر الجزء الأيسر من هذه الصورة نتيجة الدالة snap ():



لذا ، قمنا بطلاء سطحنا بثلاثة ألوان ، تقابل المحاور الثلاثة لنظام الإحداثيات. حسنًا ، ثم نضيف المعادلات التالية لكل حافة في نظامنا:

  nlRowScaling(1.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlRightHandSide(m.point(v1)[d] - m.point(v2)[d]); nlEnd(NL_ROW); 

بمعنى ، نطلب من كل حافة سطح الإخراج أن تشبه الحافة المقابلة لسطح الإدخال ، وصلابة الزنبرك 1. ومن ثم ، إذا سمحنا ، على سبيل المثال ، البعد x ، والحافة يجب أن تكون رأسية ، فإننا نقول ببساطة أن رأسًا واحدًا يساوي الطرف الآخر بصلابة الزنبرك 2:

  nlRowScaling(2.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlEnd(NL_ROW); 

حسنًا ، إليكم نتيجة برنامجنا:



سؤال معقول تمامًا: الأصنام من جزيرة إيستر ، هذا بالطبع أمر رائع ، لكن ما علاقة الجيولوجيا به؟ هل هناك أي أمثلة للمشاكل الحقيقية؟

نعم بالطبع.لنأخذ قسمًا واحدًا من قشرة الأرض:



بالنسبة إلى الجيولوجيين ، فإن طبقات الصخور المختلفة مهمة جدًا ، حيث تظهر الحدود (آفاق) باللون الأخضر ، والأخطاء الجيولوجية التي تظهر باللون الأحمر. لدينا عند إدخال شبكة من المثلثات (رباعي السطوح ثلاثية الأبعاد) في المنطقة التي تهمنا ، ولكن هناك حاجة إلى الكواد (سداسي الشكل في ثلاثي الأبعاد) لتصميم عمليات معينة. نقوم بتشويه نموذجنا بحيث تصبح العيوب رأسية والآفاق (مفاجأة) أفقية:



بعد ذلك نأخذ شبكة مربعات منتظمة ، ونقطع مجالنا إلى مربعات موحدة ، ونطبق التحول العكسي عليها ، ونحصل على الشبكة اللازمة من الكواد.

استنتاج

تعد أساليب المربعات الصغرى أداة قوية لمعالجة البيانات ، ويتم استخدامها على نطاق أوسع بكثير من الإحصاءات الموجودة في أعمدة Excel. يتم فتح هذه الاحتمالات لنا نظرًا لحقيقة أن التقليل إلى أدنى حد من الوظيفة التربيعية وحل نظام من المعادلات الخطية هي واحدة ونفس الشيء ، وقد تعلمنا (الإنسانية) حل المعادلات الخطية بشكل جيد للغاية ، وحتى أحجام غير إنسانية تمامًا بمليارات من المتغيرات.

ومع ذلك ، هناك أوقات قد لا يكون لدينا فيها نماذج خطية كافية. وهنا ، على سبيل المثال ، يمكن للشبكات العصبية أن تنقذ. في المقالة التالية ، سأحاول إظهار أن OLS مع رفض الانبعاثات يعادل واحدة من تركيبات الشبكات العصبية. ابق على الخط!