RayTracing مفهومة في 256 خطوط من C ++ العارية

هذا فصل آخر من محاضرتي الموجزة حول رسومات الكمبيوتر . هذه المرة نحن نتحدث عن تتبع الأشعة. كالعادة ، أحاول تجنب مكتبات الجهات الخارجية ، حيث أعتقد أنها تجعل الطلاب يتحققون مما يحدث تحت الغطاء. تحقق أيضًا من مشروع tinykaboom .

هناك الكثير من مقالات raytracing على الويب ؛ ومع ذلك ، فإن المشكلة تكمن في أن جميعها تقريبًا تعرض برامج مكتملة يصعب فهمها. خذ على سبيل المثال تحدي بطاقة businness الخاص بتتبع راي . إنه ينتج برامج مثيرة للإعجاب للغاية ، لكن من الصعب للغاية فهم كيف يعمل هذا. بدلاً من إظهار أنه يمكنني تقديم عروض ، أريد أن أخبرك بالتفصيل كيف يمكنك القيام بذلك بنفسك.

ملاحظة: ليس من المنطقي مجرد إلقاء نظرة على الكود ، ولا مجرد قراءة هذه المقالة مع كوب من الشاي في متناول اليد. تم تصميم هذه المقالة لتتمكن من تناول لوحة المفاتيح وتنفيذ محرك العرض الخاص بك. سيكون بالتأكيد أفضل مني. على الأقل تغيير لغة البرمجة!

لذلك ، فإن الهدف اليوم هو معرفة كيفية تقديم مثل هذه الصور:

الخطوة 1: كتابة صورة على القرص

لا أريد أن أزعج مديري النوافذ ومعالجة الماوس / لوحة المفاتيح وأشياء من هذا القبيل. ستكون نتيجة برنامجنا صورة بسيطة محفوظة على القرص. لذا ، فإن أول ما نحتاج إلى القيام به هو حفظ الصورة على القرص. هنا يمكنك العثور على الكود الذي يسمح لنا بذلك. اسمحوا لي أن سرد الملف الرئيسي:

#include <limits> #include <cmath> #include <iostream> #include <fstream> #include <vector> #include "geometry.h" void render() { const int width = 1024; const int height = 768; std::vector<Vec3f> framebuffer(width*height); for (size_t j = 0; j<height; j++) { for (size_t i = 0; i<width; i++) { framebuffer[i+j*width] = Vec3f(j/float(height),i/float(width), 0); } } std::ofstream ofs; // save the framebuffer to file ofs.open("./out.ppm"); ofs << "P6\n" << width << " " << height << "\n255\n"; for (size_t i = 0; i < height*width; ++i) { for (size_t j = 0; j<3; j++) { ofs << (char)(255 * std::max(0.f, std::min(1.f, framebuffer[i][j]))); } } ofs.close(); } int main() { render(); return 0; } 

يتم تقديم render () فقط في الوظيفة الرئيسية ولا شيء آخر. ما هو داخل وظيفة التقديم ()؟ أولاً وقبل كل شيء ، أقوم بتعريف إطار المكياج على شكل صفيف أحادي البعد لقيم Vec3f ، وهي عبارة عن متجهات ثلاثية الأبعاد بسيطة تمنحنا قيم (ص ، ز ، ب) لكل بكسل. تعيش فئة المتجهات في هندسة الملفات. h ، لن أصفها هنا: إنها بالفعل معالجة تافهة لمتجهات ثنائية وثلاثية الأبعاد (إضافة وطرح وتعيين وضرب بمنتج عددي أو منتج عددي).

أحفظ الصورة بتنسيق ppm . إنها أسهل طريقة لحفظ الصور ، ولكن ليس دائمًا الطريقة الأكثر ملاءمة لعرضها بشكل أكبر. إذا كنت تريد الحفظ في تنسيقات أخرى ، فإنني أوصي بربط مكتبة تابعة لجهة خارجية ، مثل stb . هذه مكتبة رائعة: تحتاج فقط إلى تضمين ملف رأس واحد stb_image_write.h في المشروع ، وسيسمح لك بحفظ الصور بأكثر التنسيقات شيوعًا.

تحذير: الكود الخاص بي ممتلئ بالأخطاء ، وأصلحها في مرحلة ما بعد الإنتاج ، لكن الالتزامات القديمة تتأثر. تحقق هذه المشكلة .

لذا ، فإن الهدف من هذه الخطوة هو التأكد من أننا قادرون على) إنشاء صورة في الذاكرة + تعيين ألوان مختلفة و (ب) حفظ النتيجة على القرص. ثم يمكنك مشاهدته في برنامج تابع لجهة خارجية. هذه هي النتيجة:

الخطوة 2 ، واحدة حاسمة: تتبع الأشعة

هذه هي الخطوة الأكثر أهمية وصعوبة في السلسلة بأكملها. أريد تحديد مجال واحد في الكود الخاص بي وارسمه دون أن يكون مهووسًا بالمواد أو الإضاءة. هذه هي الطريقة التي يجب أن تبدو بها نتيجة:

من أجل الراحة ، لدي التزام واحد لكل خطوة في مستودع التخزين الخاص بي ؛ يجعل Github من السهل جدًا عرض التغييرات التي تم إجراؤها. هنا ، على سبيل المثال ، ما تم تغييره بواسطة الالتزام الثاني.

بادئ ذي بدء ، ما الذي نحتاجه لتمثيل المجال في ذاكرة الكمبيوتر؟ أربعة أرقام تكفي: متجه ثلاثي الأبعاد لمركز الكرة وعدد قياسي يصف نصف القطر:

 struct Sphere { Vec3f center; float radius; Sphere(const Vec3f &c, const float &r) : center(c), radius(r) {} bool ray_intersect(const Vec3f &orig, const Vec3f &dir, float &t0) const { Vec3f L = center - orig; float tca = L*dir; float d2 = L*L - tca*tca; if (d2 > radius*radius) return false; float thc = sqrtf(radius*radius - d2); t0 = tca - thc; float t1 = tca + thc; if (t0 < 0) t0 = t1; if (t0 < 0) return false; return true; } }; 

الشيء الوحيد غير التافه في هذا الكود هو الوظيفة التي تسمح لك بالتحقق مما إذا كان شعاع معين (مصدره الأصل في اتجاه دير) يتقاطع مع منطقتنا. يمكن العثور هنا على وصف تفصيلي للخوارزمية الخاصة بتقاطع شعاع الكرة ، ونوصيك بشدة أن تفعل ذلك وتحقق من الكود.

كيف يعمل تتبع الأشعة؟ انها بسيطة جدا. في الخطوة الأولى ، ملأنا الصورة بتدرج من الألوان:

  for (size_t j = 0; j<height; j++) { for (size_t i = 0; i<width; i++) { framebuffer[i+j*width] = Vec3f(j/float(height),i/float(width), 0); } } 

الآن لكل بكسل ، سنشكل شعاع قادم من الأصل ويمر عبر بكسلنا ، ومن ثم تحقق مما إذا كان هذا الشعاع يتقاطع مع الكرة:

إذا لم يكن هناك تقاطع مع الكرة فنحن نرسم البيكسل بالألوان 1 ، وإلا بالألوان 2:

 Vec3f cast_ray(const Vec3f &orig, const Vec3f &dir, const Sphere &sphere) { float sphere_dist = std::numeric_limits<float>::max(); if (!sphere.ray_intersect(orig, dir, sphere_dist)) { return Vec3f(0.2, 0.7, 0.8); // background color } return Vec3f(0.4, 0.4, 0.3); } void render(const Sphere &sphere) {  [...] for (size_t j = 0; j<height; j++) { for (size_t i = 0; i<width; i++) { float x = (2*(i + 0.5)/(float)width - 1)*tan(fov/2.)*width/(float)height; float y = -(2*(j + 0.5)/(float)height - 1)*tan(fov/2.); Vec3f dir = Vec3f(x, y, -1).normalize(); framebuffer[i+j*width] = cast_ray(Vec3f(0,0,0), dir, sphere); } }  [...] } 

في هذه المرحلة ، أوصيك بأخذ قلم رصاص والتحقق على الورق من جميع الحسابات (تقاطع كرة الشعاع واجتاح الصورة بالأشعة). فقط في حالة ، يتم تحديد الكاميرا لدينا من خلال الأشياء التالية:

• عرض الصورة
• ارتفاع الصورة
• مجال زاوية الرؤية
• موقع الكاميرا ، Vec3f (0.0.0)
• عرض الاتجاه ، على طول المحور z ، في اتجاه ناقص اللانهاية

اسمحوا لي أن أوضح كيف نحسب الاتجاه الأولي للأشعة لتتبع. في الحلقة الرئيسية لدينا هذه الصيغة:

  float x = (2*(i + 0.5)/(float)width - 1)*tan(fov/2.)*width/(float)height; float y = -(2*(j + 0.5)/(float)height - 1)*tan(fov/2.); 

من أين يأتي؟ بسيط جدا. يتم وضع الكاميرا لدينا في الأصل وتواجه الاتجاه -z. اسمحوا لي أن أوضح الأشياء ، هذه الصورة تظهر الكاميرا من الأعلى ، محور y خارج الشاشة:

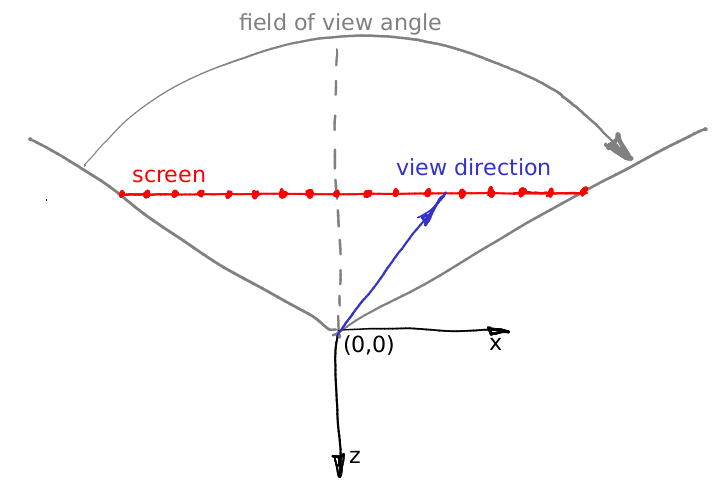
كما قلت ، يتم وضع الكاميرا في الأصل ، ويتم عرض المشهد على الشاشة التي تقع في المستوى z = -1. يحدد مجال الرؤية قطاع المساحة الذي سيكون مرئيًا على الشاشة. في الصورة لدينا الشاشة 16 بكسل. يمكنك حساب طوله في إحداثيات العالم؟ إنها بسيطة: دعنا نركز على المثلث الذي يتكون من الخط الأحمر والرمادي والرمادي المتقطع. من السهل أن ترى أن تان (مجال الرؤية / 2) = (عرض الشاشة) 0.5 / (مسافة كاميرا الشاشة). وضعنا الشاشة على مسافة 1 من الكاميرا ، وبالتالي (عرض الشاشة) = 2 تان (مجال الرؤية / 2).

الآن دعنا نقول أننا نريد أن نوجه متجهًا من خلال مركز البيكسل الثاني عشر من الشاشة ، أي نريد حساب المتجه الأزرق. كيف يمكننا أن نفعل ذلك؟ ما هي المسافة من يسار الشاشة إلى طرف المتجه الأزرق؟ بادئ ذي بدء ، هو 12 + 0.5 بكسل. نحن نعلم أن 16 بكسل للشاشة تتوافق مع وحدتين عالميتين تان (fov / 2). وهكذا ، يقع طرف المتجه في (12 + 0.5) / 16 2 تان (fov / 2) وحدات العالم من الحافة اليسرى ، أو على مسافة (12 + 0.5) 2/16 * تان (fov / 2) - تان (fov / 2) من التقاطع بين الشاشة والمحور -z. أضف نسبة أبعاد الشاشة إلى الحسابات وستجد بالضبط صيغ اتجاه الشعاع.

الخطوة 3: إضافة المزيد من المجالات

الجزء الأصعب قد انتهى ، والآن طريقنا واضح. إذا كنا نعرف كيفية رسم كرة واحدة ، فلن يستغرق الأمر وقتًا طويلاً لإضافة المزيد. تحقق من التغييرات في الكود ، وهذه هي الصورة الناتجة:

الخطوة 4: الإضاءة

الصورة مثالية في جميع الجوانب ، باستثناء قلة الضوء. خلال بقية المقال سنتحدث عن الإضاءة. دعنا نضيف مصادر ضوئية قليلة:

 struct Light { Light(const Vec3f &p, const float &i) : position(p), intensity(i) {} Vec3f position; float intensity; }; 

تعد عملية حساب الإضاءة العالمية الحقيقية مهمة بالغة الصعوبة ، لذا ، مثل أي شخص آخر ، سوف نخدع العين من خلال رسم نتائج غير مادية تمامًا ، لكنها معقولة بصريًا. بادئ ذي بدء: لماذا يكون الجو باردًا في الشتاء وحارًا في الصيف؟ لأن تسخين سطح الأرض يعتمد على زاوية حدوث أشعة الشمس. كلما ارتفعت الشمس فوق الأفق ، كان السطح أكثر إشراقًا. وعلى العكس من ذلك ، كلما كان أعلى من الأفق ، كان لونه باهتًا. وبعد أن تغرب الشمس عن الأفق ، لا تصلنا الفوتونات مطلقًا.

رجوع أجواءنا: نصدر أشعة من الكاميرا (لا علاقة للفوتونات!) وهو يتوقف عند كرة. كيف نعرف شدة نقطة تقاطع الإضاءة؟ في الواقع ، يكفي التحقق من الزاوية بين المتجه الطبيعي في هذه النقطة والمتجه الذي يصف اتجاه الضوء. أصغر زاوية ، كان السطح أفضل مضاءة. تذكر أن المنتج القياسي بين متجهين a و b يساوي ناتج قواعد المتجهات ضرب جيب تمام الزاوية بين المتجهات: a * b = | a | | ب | كوس (ألفا (أ ، ب)). إذا أخذنا نواقل بطول الوحدة ، فإن منتج النقطة سوف يعطينا كثافة إضاءة السطح.

وبالتالي ، في وظيفة cast_ray ، بدلاً من اللون الثابت ، سنقوم بإعادة اللون مع مراعاة مصادر الضوء:

 Vec3f cast_ray(const Vec3f &orig, const Vec3f &dir, const Sphere &sphere) { [...] float diffuse_light_intensity = 0; for (size_t i=0; i<lights.size(); i++) { Vec3f light_dir = (lights[i].position - point).normalize(); diffuse_light_intensity += lights[i].intensity * std::max(0.f, light_dir*N); } return material.diffuse_color * diffuse_light_intensity; } 

التعديلات wrt الخطوة السابقة متوفرة هنا ، وهنا هي النتيجة:

الخطوة 5: الإضاءة براق

تقدم خدعة نقطة المنتج تقريبًا جيدًا لإضاءة الأسطح غير اللامعة ، في الأدب يطلق عليه الإضاءة المنتشرة. ما الذي يجب أن نفعله إذا أردنا رسم أسطح لامعة؟ أريد الحصول على صورة مثل هذا:

تحقق من عدد التعديلات الضرورية. باختصار ، كلما كان الضوء على الأسطح اللامعة أكثر إشراقًا ، قلت الزاوية بين اتجاه العرض واتجاه الضوء المنعكس .

تُعرف هذه الخدعة المزودة بإضاءة الأسطح اللامعة والممتعة باسم نموذج انعكاس فونج . تحتوي الويكي على وصف مفصل إلى حد ما لنموذج الإضاءة هذا. قد يكون من الجيد قراءتها جنبًا إلى جنب مع الكود المصدري. هذه هي الصورة الأساسية لفهم السحر:

الخطوة 6: الظلال

لماذا لدينا الضوء ، ولكن لا ظلال؟ هذا ليس بخير! اريد هذه الصورة

مجرد ستة سطور من الكود تسمح لنا بتحقيق هذا: عند رسم كل نقطة ، نحن فقط نتأكد من أن المقطع بين النقطة الحالية ومصدر الضوء لا يتقاطع مع كائنات مشهدنا. إذا كان هناك تقاطع ، فإننا نتخطى مصدر الضوء الحالي. لا يوجد سوى دقة صغيرة: أزعج النقطة بتحريكها في الاتجاه الطبيعي:

 Vec3f shadow_orig = light_dir*N < 0 ? point - N*1e-3 : point + N*1e-3; 

لماذا هذا؟ إنها مجرد نقطة تكمن في سطح الكائن ، و (باستثناء مسألة الأخطاء العددية) فإن أي شعاع من هذه النقطة سيتقاطع مع الكائن نفسه.

الخطوة 7: الانعكاسات

إنه أمر لا يصدق ، ولكن لإضافة تأملات إلى عرضنا ، نحتاج فقط إلى إضافة ثلاثة سطور من التعليمات البرمجية:

  Vec3f reflect_dir = reflect(dir, N).normalize(); Vec3f reflect_orig = reflect_dir*N < 0 ? point - N*1e-3 : point + N*1e-3; // offset the original point to avoid occlusion by the object itself Vec3f reflect_color = cast_ray(reflect_orig, reflect_dir, spheres, lights, depth + 1); 

يمكنك رؤيته بنفسك: عند تقاطع الكرة ، نحسب فقط الأشعة المنعكسة (بمساعدة نفس الوظيفة التي استخدمناها للضوء البارز!) وندعو بشكل متكرر بوظيفة cast_ray في اتجاه الشعاع المنعكس. تأكد من اللعب بعمق العودية ، لقد قمت بضبطه على 4 ، جرب قيمًا مختلفة تبدأ من 0 ، ما الذي سيتغير في الصورة؟ هذه هي نتيجة بلدي مع انعكاسات وعمق العودية من 4:

الخطوة 8: الانكسار

إذا كنا نعلم أن نفكر ملياً ، فإن الانكسارات تكون سهلة . نحتاج إلى إضافة دالة واحدة لحساب الشعاع المنكسر ( باستخدام قانون Snell ) ، وثلاثة أسطر أخرى من الكود في دالة cast_ray العودية. هذه هي النتيجة حيث تكون أقرب كرة "مصنوعة من الزجاج" ، فهي تنعكس وتنعكس الضوء في نفس الوقت:

ستو 9: وراء المجالات

حتى هذه اللحظة ، قمنا بتقديم كرات فقط لأنها واحدة من أبسط الكائنات الرياضية غير التافهة. دعونا نضيف طائرة. رقعة الشطرنج هي الاختيار الكلاسيكي. لهذا الغرض ، يكفي إضافة عشرات الخطوط .

وهنا النتيجة:

كما وعدت ، الكود يحتوي على 256 سطرًا من الشفرة ، تحقق من ذلك بنفسك !

الخطوة 10: مهمة المنزل

لقد قطعنا شوطًا طويلًا: لقد تعلمنا كيفية إضافة كائنات إلى مشهد ما ، وكيفية حساب الإضاءة المعقدة إلى حد ما. اسمحوا لي أن أترك لك مهمتين كواجب منزلي. تماما كل الأعمال التحضيرية قد تم بالفعل في فرع الواجب المنزلي . سيتطلب كل مهمة عشرة أسطر من قمم الشفرات.

الاحالة 1: خريطة البيئة

في الوقت الحالي ، إذا لم تتقاطع الأشعة مع أي كائن ، فسنقوم فقط بتعيين البيكسل على لون الخلفية الثابت. ولماذا ، في الواقع ، هل هو ثابت؟ دعنا نلتقط صورة كروية (file envmap.jpg ) ونستخدمها كخلفية! لجعل الحياة أسهل ، قمت بربط مشروعنا مع مكتبة stb لتوفير الراحة في العمل بتنسيق jpg. يجب أن تعطينا هذه الصورة:

الواجب 2: الدجال الدجال!

يمكننا تقديم كل من الطائرات والطائرات (انظر الشطرنج). لذلك دعونا رسم تنسجم المثلث! لقد كتبت رمزًا يسمح لك بقراءة ملف .obj ، وأضفت إليه وظيفة تقاطع مثلث الأشعة. الآن يجب أن تكون إضافة البطة إلى مشهدنا تافهة للغاية:

استنتاج

هدفي الرئيسي هو إظهار المشروعات المثيرة للاهتمام (والسهلة!) للبرنامج. أنا مقتنع بأنه لكي تصبح مبرمجًا جيدًا ، يجب أن تقوم بالكثير من المشاريع الجانبية. لا أعلم عنك ، لكنني شخصياً لست منجذباً إلى برنامج المحاسبة ولعبة كاسحة ألغام ، حتى لو كان تعقيد الكود مشابهًا تمامًا.

بضع ساعات ومئتان وخمسون سطرًا من التعليمات البرمجية يعطينا رايتراسير. يمكن إجراء خمسمائة سطر من برنامج تنقيط البرنامج في غضون أيام قليلة. الرسومات رائعة حقا لتعلم البرمجة!