بطولة البرمجة الثانية: نقوم بتحليل مهام المسار ML

في أكتوبر ، عقدت بطولة البرمجة الثانية. تلقينا 12500 طلب ، جرب أكثر من 6000 شخص أيديهم في المسابقات. هذه المرة ، يمكن للمشاركين اختيار أحد المسارات التالية: الخلفية ، الواجهة الأمامية ، تطوير الأجهزة المحمولة والتعلم الآلي. في كل مسار ، كان لا بد من اجتياز مرحلة التأهيل والنهائي.

حسب التقاليد ، سننشر تحليل المسارات على حبري. لنبدأ بمهام مرحلة التأهيل للتعلم الآلي. أعد الفريق خمس مهام من هذا القبيل ، كان هناك خياران لثلاث مهام: في الإصدار الأول كانت هناك مهام A1 و B1 و C ، في الثانية - A2 و B2 و C. تم توزيع الخيارات بشكل عشوائي بين المشاركين. مؤلف المهمة C هو مطورنا Pavel Parkhomenko ، وتم إجراء بقية المهام بواسطة زميله نيكيتا سيندروفيتش.

لأول مهمة حسابية بسيطة (A1 / A2) ، يمكن للمشاركين الحصول على 50 نقطة عن طريق تعداد الإجابة بشكل صحيح. بالنسبة للمهمة الثانية (B1 / B2) قدمنا ​​من 10 إلى 100 نقطة - اعتمادًا على فعالية الحل. للحصول على 100 نقطة ، كان مطلوبًا تنفيذ طريقة البرمجة الديناميكية. تم تكريس المهمة الثالثة لإنشاء نموذج النقر بناءً على بيانات التدريب المقدمة. يتطلب الأمر تطبيق أساليب العمل مع السمات الفئوية واستخدام نموذج غير خطي للتدريب (على سبيل المثال ، تعزيز التدرج). بالنسبة للمهمة ، كان من الممكن الحصول على ما يصل إلى 150 نقطة - حسب قيمة وظيفة الخسارة في عينة الاختبار.

A1. استعادة طول دائري

حالة

يجب أن يحدد نظام التوصيات بشكل فعال مصالح الناس. بالإضافة إلى أساليب التعلم الآلي ، يتم استخدام حلول واجهة خاصة لتنفيذ هذه المهمة ، والتي تسأل المستخدم بوضوح ما هو مثير للاهتمام بالنسبة له. واحد مثل هذا الحل هو دائري.

دائري هو شريط أفقي من البطاقات ، كل منها يعرض الاشتراك في مصدر أو موضوع محدد. يمكن العثور على البطاقة نفسها في الكاروسيل عدة مرات. يمكن تمرير دائري من اليسار إلى اليمين ، في حين يرى المستخدم مرة أخرى البطاقة الأولى بعد آخر بطاقة. بالنسبة للمستخدم ، فإن الانتقال من البطاقة الأخيرة إلى الأولى غير مرئي ، ومن وجهة نظره فإن الشريط لا ينتهي.

في مرحلة ما ، لاحظ مستخدم فضولي فاسيلي أن الشريط كان في الواقع محلقًا ، وقرر معرفة الطول الحقيقي للدائرة. للقيام بذلك ، بدأ التمرير عبر الشريط وكتابة بطاقات الاجتماع بالتتابع ، من أجل البساطة ، مع تحديد كل بطاقة بحرف لاتيني صغير. لذلك كتب فاسيلي البطاقات الأولى على قطعة من الورق. ويضمن أنه نظر إلى جميع بطاقات الكاروسيل مرة واحدة على الأقل. ثم ذهب فاسيلي إلى الفراش ، وفي الصباح اكتشف أن شخصًا قد سُكب كوبًا من الماء على ملاحظاته ، والآن يتعذر التعرف على بعض الحروف.

وفقًا للمعلومات المتبقية ، ساعد فاسيلي في تحديد أصغر عدد ممكن من البطاقات في الكاروسيل.

نظام التقييم

فقط بعد اجتياز جميع اختبارات المهمة ، يمكنك الحصول على 50 نقطة .

في نظام الاختبار ، تعتبر الاختبارات من 1 إلى 4 أمثلة من الحالة.

قرار

كان كافياً لفرز الطول المحتمل للدوائر من 1 إلى n ولكل فحص طول ثابت إذا كان يمكن أن يكون كذلك. من الواضح أن الإجابة موجودة دائمًا ، لأن قيمة n مضمونة لتكون إجابة ممكنة. بالنسبة لطول دائري ثابت p ، يكفي التحقق من أنه في السلسلة المرسلة للجميع i من 0 إلى (p - 1) في جميع المواضع i ، i + p ، i + 2p ، وما إلى ذلك ، تم العثور على الأحرف نفسها أو #. إذا كان هناك على الأقل بالنسبة لشخص ما شخصيتان مختلفتان من النطاق من a إلى z ، فلا يمكن للطول دائري أن يكون طوله p. نظرًا لأنه في أسوأ الحالات ، في كل p ، تحتاج إلى تشغيل كل أحرف السلسلة مرة واحدة ، وتعقيد هذه الخوارزمية هو O (n ² ).

 def check_character(char, curchar): return curchar is None or char == "#" or curchar == char def need_to_assign_curchar(char, curchar): return curchar is None and char != "#" n = int(input()) s = input().strip() for p in range(1, n + 1): is_ok = True for i in range(0, p): curchar = None for j in range(i, n, p): if not check_character(s[j], curchar): is_ok = False break if need_to_assign_curchar(s[j], curchar): curchar = s[j] if not is_ok: break if is_ok: print(p) break 

A2. استعادة طول دائري

حالة

يجب أن يحدد نظام التوصيات بشكل فعال مصالح الناس. بالإضافة إلى أساليب التعلم الآلي ، يتم استخدام حلول واجهة خاصة لتنفيذ هذه المهمة ، والتي تسأل المستخدم بوضوح ما هو مثير للاهتمام بالنسبة له. واحد مثل هذا الحل هو دائري.

دائري هو شريط أفقي من البطاقات ، كل منها يعرض الاشتراك في مصدر أو موضوع محدد. يمكن العثور على البطاقة نفسها في الكاروسيل عدة مرات. يمكن تمرير دائري من اليسار إلى اليمين ، في حين يرى المستخدم مرة أخرى البطاقة الأولى بعد آخر بطاقة. بالنسبة للمستخدم ، فإن الانتقال من البطاقة الأخيرة إلى الأولى غير مرئي ، ومن وجهة نظره فإن الشريط لا ينتهي.

في مرحلة ما ، لاحظ مستخدم فضولي فاسيلي أن الشريط كان في الواقع محلقًا ، وقرر معرفة الطول الحقيقي للدائرة. للقيام بذلك ، بدأ التمرير عبر الشريط وكتابة بطاقات الاجتماع بالتتابع ، من أجل البساطة ، مع تحديد كل بطاقة بحرف لاتيني صغير. لذلك كتب فاسيلي أول بطاقات ن. ويضمن أنه نظر إلى جميع بطاقات الكاروسيل مرة واحدة على الأقل. نظرًا لأن فاسيلي كان مشتتًا بمحتويات البطاقات ، عند الكتابة ، يمكنه أن يستبدل بطريق الخطأ حرفًا بحرف آخر ، لكن من المعروف أنه لم يرتكب أية أخطاء في المجموع.

سقطت التسجيلات التي قام بها فاسيلي في يديك ؛ أنت تعرف أيضًا قيمة k. تحديد عدد البطاقات التي يمكن أن تكون في دائري له.

نظام التقييم

فقط بعد اجتياز جميع اختبارات المهمة ، يمكنك الحصول على 50 نقطة .

في نظام الاختبار ، تعتبر الاختبارات من 1 إلى 4 أمثلة من الحالة.

قرار

كان كافياً لفرز الطول المحتمل للدوائر من 1 إلى n ولكل فحص طول ثابت إذا كان يمكن أن يكون كذلك. من الواضح أن الإجابة موجودة دائمًا ، نظرًا لأن قيمة n مضمونة لتكون إجابة ممكنة ، مهما كانت قيمة k. بالنسبة لطول دائري ثابت p ، يكفي حساب كل i بشكل مستقل من 0 إلى (p - 1) ما هو الحد الأدنى لعدد الأخطاء التي يتم إجراؤها في المواضع i و i + p و i + 2p وما إلى ذلك. الرمز هو الذي يوجد في هذه المواقف في أغلب الأحيان. ثم عدد الأخطاء يساوي عدد المواقف التي يقف عليها حرف آخر. إذا كان العدد الإجمالي للأخطاء في بعض الحالات لا يتجاوز k ، فإن القيمة p هي إجابة محتملة. نظرًا لأن كل عطل تحتاج إلى تجاوز كل أحرف السلسلة مرة واحدة ، فإن تعقيد هذه الخوارزمية هو O (n ² ).

 n, k = map(int, input().split()) s = input().strip() for p in range(1, n + 1): mistakes = 0 for i in range(0, p): counts = [0] * 26 for j in range(i, n, p): counts[ord(s[j]) - ord("a")] += 1 mistakes += sum(counts) - max(counts) if mistakes <= k: print(p) break 

B1. شريط التوصية الأمثل

حالة

إن تكوين الجزء التالي من الإصدار الشخصي للتوصيات للمستخدم ليس بالأمر السهل. ضع في اعتبارك n المنشورات التي تم اختيارها من قاعدة توصية بناءً على اختيار المرشحين. رقم المنشور i يتميز بدرجة الملاءمة s _i ومجموعة من السمات الثنائية k _i1 و _i2 و ... و _ik . تتطابق كل من هذه السمات مع بعض خصائص المنشور ، على سبيل المثال ، ما إذا كان المستخدم مشتركًا في مصدر هذا المنشور ، وما إذا كان المنشور قد تم إنشاؤه خلال الـ 24 ساعة الماضية ، وما إلى ذلك. يمكن أن يحتوي المنشور على العديد من هذه الخصائص في وقت واحد ، وفي هذه الحالة تأخذ السمات المقابلة القيمة 1 ، أو قد لا تحتوي على أي منها - ثم تكون كل سماتها هي 0.

من أجل أن تكون خلاصة المستخدم متنوعة ، من الضروري الاختيار من بين المنشورات m بحيث يكون هناك منشورات A ₁ على الأقل تحتوي على الخاصية الأولى ، منشورات A ₂ على الأقل تحتوي على الخاصية الثانية ، ... ، منشورات A _k لها خاصية رقم ك. ابحث عن أقصى درجة ممكنة من درجة الملاءمة الكلية للمنشورات m التي تفي بهذا المطلب ، أو حدد أن هذه المجموعة من المنشورات غير موجودة.

نظام التقييم

تتكون اختبارات هذه المهمة من خمس مجموعات. يتم منح نقاط لكل مجموعة فقط عند اجتياز جميع اختبارات المجموعة وجميع اختبارات المجموعات السابقة . اجتياز الاختبارات من الشروط ضروري للحصول على نقاط للمجموعات التي تبدأ من الثانية. في المجموع لهذه المهمة يمكنك الحصول على 100 نقطة .

في نظام الاختبار ، تعتبر الاختبارات 1-2 أمثلة من الحالة.

1. (10 نقاط) الاختبارات 3-10: k = 1 ، m m 3 ، s _i ≤ 1000 ، لا يلزم إجراء اختبارات من الحالة
2. (20 نقطة) الاختبارات 11-20: k ≤ 2 ، m ≤ 3
3. (20 نقطة) الاختبارات 21-29: k ≤ 2
4. (20 نقطة) الاختبارات 30-37: k ≤ 3
5. (30 نقطة) الاختبارات 38-47: لا توجد قيود إضافية

قرار

توجد منشورات ، لكل منها أعلام السرعة والقيمة المنطقية k ، من الضروري اختيار بطاقات m بحيث يكون الحد الأقصى من النسبية ومتطلبات k للنموذج "من بين المنشورات m المحددة يجب أن تحتوي على" بطاقات A مع علامة i "، أو تحديد أن هذه المجموعة من المنشورات غير موجودة.

القرار 10 نقاط : إذا كان هناك علامة واحدة بالضبط ، يكفي أن تأخذ منشورات A ₁ مع هذه العلامة الأكثر أهمية (إذا كان هناك عدد أقل من البطاقات من A ₁ ، فإن المجموعة المطلوبة غير موجودة) ، أما البقية (m - A ₁ ) فيجب أن تلتقطها البقية بطاقات مع أفضل صلة.

الحل هو 30 نقطة : إذا لم تتجاوز m 3 ، فيمكنك إيجاد الإجابة عن طريق البحث الشامل لجميع بطاقات O (n ³ ) الممكنة ، حدد الخيار الأفضل من حيث الملاءمة الكلية التي تفي بالقيود.

القرار هو 70 نقطة (50 نقطة هي نفسها ، فقط أسهل للتنفيذ): إذا لم يكن هناك أكثر من 3 أعلام ، فيمكنك تقسيم جميع المنشورات إلى 8 مجموعات منفصلة وفقًا لمجموعة العلامات التي لديها: 000 ، 001 ، 010 ، 011 ، 100 ، 101 ، 110 ، 111. يجب فرز المنشورات في كل مجموعة بترتيب تنازلي من حيث الأهمية. بعد ذلك ، بالنسبة إلى O (م ⁴ ) ، يمكننا فرز عدد أفضل المنشورات التي نأخذها من المجموعات 111 و 011 و 110 و 101. بعد ذلك ، يصبح من الواضح عدد المنشورات التي يجب جمعها من المجموعات 100 و 010 و 001 من أجل تلبية المتطلبات. يبقى للوصول إلى م مع البطاقات المتبقية مع أفضل صلة.

الحل الكامل : ضع في الاعتبار وظيفة البرمجة الديناميكية dp [i] [a] ... [z]. هذا هو الحد الأقصى لمجموع درجة الصلة التي يمكن الحصول عليها باستخدام منشورات i بالضبط بحيث توجد المنشورات التي تحمل العلامة A ، ... ، z مع العلم Z. ثم ، مبدئيًا [0] [0] ... [0] = 0 ، وبالنسبة لجميع مجموعات المعلمات الأخرى ، قمنا بتعيين القيمة تساوي -1 من أجل زيادة هذه القيمة إلى الحد الأقصى في المستقبل. بعد ذلك ، سوف ندخل بطاقات "واحدة في اللعبة" واحدة تلو الأخرى ، ونستخدم كل بطاقة لتحسين قيم هذه الوظيفة: لكل حالة ديناميكية (i ، a ، b ، ... ، z) باستخدام المنشور j-th مع الأعلام (a _j ، b _j ، ... ، z _j ) ، يمكننا محاولة إجراء انتقال إلى الحالة (i + 1 ، a + a _j ، b + b _j ، ... ، z + z _j ) والتحقق من تحسن النتيجة في هذه الحالة. مهم: أثناء الانتقال ، لسنا مهتمين بالحالات التي لا تقل فيها الحالات الكلية لهذه الديناميات عن m ^{k + 1} ، والسلوك المقارب الناتج هو O (nm ^{k + 1} ). عندما يتم حساب حالات الديناميات ، تكون الإجابة هي حالة تفي بالقيود وتعطي أعلى درجة من درجة الأهمية الكلية.

من وجهة نظر التنفيذ ، من المفيد تخزين حالة البرمجة الديناميكية وأعلام كل منشور في شكل معبأ برقم واحد كامل لتسريع عمل البرنامج (انظر الكود) ، وليس في قائمة أو مجموعة. يستخدم هذا الحل ذاكرة أقل ويسمح لك بتحديث حالة الديناميات بفعالية.

كود الحل الكامل:

 def pack_state(num_items, counts): result = 0 for count in counts: result = (result << 8) + count return (result << 8) + num_items def get_num_items(state): return state & 255 def get_flags_counts(state, num_flags): flags_counts = [0] * num_flags state >>= 8 for i in range(num_flags): flags_counts[num_flags - i - 1] = state & 255 state >>= 8 return flags_counts n, m, k = map(int, input().split()) scores, attributes = [], [] for i in range(n): score, flags = input().split() scores.append(int(score)) attributes.append(list(map(int, flags))) limits = list(map(int, input().split())) dp = {0 : 0} for i in range(n): score = scores[i] state_delta = pack_state(1, attributes[i]) dp_temp = {} for state, value in dp.items(): if get_num_items(state) >= m: continue new_state = state + state_delta if value + score > dp.get(new_state, -1): dp_temp[new_state] = value + score dp.update(dp_temp) best_score = 0 for state, value in dp.items(): if get_num_items(state) != m: continue flags_counts = get_flags_counts(state, k) satisfied_bounds = True for i in range(k): if flags_counts[i] < limits[i]: satisfied_bounds = False break if not satisfied_bounds: continue if value > best_score: best_score = value print(best_score) 

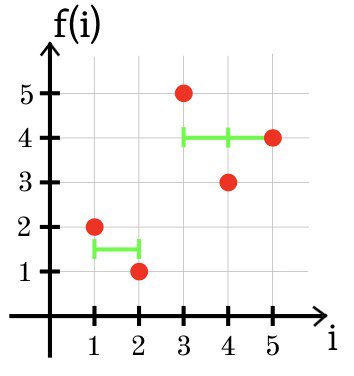
B2. تقريب وظيفة

حالة

لتقييم درجة أهمية المستندات ، يتم استخدام أساليب تعلم الآلة المختلفة - على سبيل المثال ، أشجار القرارات. تحتوي شجرة قرار k-ary على قاعدة قرار في كل عقدة تقسم الكائنات إلى فئات k وفقًا لقيم بعض السمات. في الممارسة العملية ، وعادة ما تستخدم الأشجار قرار ثنائي. النظر في نسخة مبسطة من مشكلة التحسين ، والتي يجب حلها في كل عقدة من شجرة القرار k-ary.

دع الدالة المنفصلة f محددة عند النقاط i = 1 ، 2 ، ... ، n. من الضروري إيجاد دالة ثابتة تدريجية g تتكون من ما لا يزيد عن k من أقسام الثبات بحيث تكون القيمة SSE = $$$\ sum_ {i = 1} ^ n$ (g (i) - f (i)) ^{2 هي} الحد الأدنى.

نظام التقييم

تتكون اختبارات هذه المهمة من خمس مجموعات. يتم منح نقاط لكل مجموعة فقط عند اجتياز جميع اختبارات المجموعة وجميع اختبارات المجموعات السابقة . اجتياز الاختبارات من الشروط ضروري للحصول على نقاط للمجموعات التي تبدأ من الثانية. في المجموع لهذه المهمة يمكنك الحصول على 100 نقطة .

في نظام الاختبار ، تعتبر الاختبارات 1-3 أمثلة من الحالة.

1. (10 نقاط) الاختبارات 4-22: ك = 1 ، لا توجد اختبارات مطلوبة من الشرط
2. (20 نقطة) الاختبارات 23-28: k ≤ 2
3. (20 نقطة) الاختبارات 29-34: k ≤ 3
4. (20 نقطة) اختبارات 35-40: ك ≤ 4
5. (30 نقطة) الاختبارات 41-46: لا توجد قيود إضافية

قرار

كما تعلمون ، الثابت الذي يقلل من قيمة SSE لمجموعة من القيم f ₁ ، f ₂ ، ... ، f _n هو متوسط ​​القيم المذكورة هنا. علاوة على ذلك ، لأنه من السهل التحقق من خلال العمليات الحسابية البسيطة ، فإن القيمة SSE = $$$sum \ square \ values ​​\ - \ frac {square \ sum \ values} {n}$ .

القرار 10 نقاط : نحن ببساطة نعتبر متوسط ​​جميع قيم الوظيفة و SSE كـ O (n).

القرار هو 30 نقطة : نقوم بترتيب النقطة الأخيرة المتعلقة بالجزء الأول من ثبات الاثنين ، بالنسبة للقسم الثابت نحسب SSE ونختار النقطة المثلى. بالإضافة إلى ذلك ، من المهم ألا ننسى تفكيك القضية عندما يكون هناك قسم واحد فقط من الثبات. الصعوبة - يا (ن ² ).

القرار هو 50 نقطة : نقوم بتصنيف حدود التقسيم إلى أقسام من الثبات بالنسبة لـ O (n ² ) ، وللقسم الثابت إلى 3 قطاعات ، نقوم بحساب SSE واختيار الجزء الأمثل. الصعوبة - يا (ن ³ ).

القرار هو 70 نقطة : نقوم بحساب مبالغ ومربعات المربعات الخاصة بقيم f _i على البادئات ، وسيقوم هذا بحساب المتوسط ​​و SSE بسرعة على أي مقطع. نقوم بتصنيف حدود القسم إلى 4 أقسام من الثبات لـ O (n ³ ) ، باستخدام القيم المحسوبة مسبقًا على البادئات لـ O (1) ، نقوم بحساب SSE. الصعوبة - يا (ن ³ ).

الحل الكامل : فكر في وظيفة البرمجة الديناميكية dp [s] [i]. هذه هي أصغر قيمة لـ SSE إذا قمنا بتقدير قيمة i الأولى باستخدام شرائح s. ثم
dp [0] [0] = 0 ، وبالنسبة لجميع مجموعات المعلمات الأخرى ، نقوم بتعيين القيمة مساوية لـ infinity من أجل تقليل هذه القيمة إلى الحد الأدنى. سنقوم بحل المشكلة ، وزيادة قيمة s تدريجيا. كيف يتم حساب dp [s] [i] إذا كانت قيم الديناميات لكل s أصغر يتم حسابها بالفعل؟ يكفي تعيين عدد النقاط الأولى التي تغطيها الأجزاء (s - 1) السابقة ، وترتيب جميع قيم t ، وتقريب النقاط المتبقية (i - t) باستخدام الجزء المتبقي. من الضروري اختيار أفضل قيمة t لـ SSE النهائي عند نقاط i. إذا قمنا بحساب مجموع ومربعات المربعات الخاصة بقيم f _i على البادئات ، فسيتم إجراء هذا التقريب في O (1) ، ويمكن حساب القيمة dp [s] [i] في O (n). الجواب النهائي هو موانئ دبي [ك] [ن]. التعقيد الكلي للخوارزمية هو O (kn ² ).

كود الحل الكامل:

 n, k = map(int, input().split()) f = list(map(float, input().split())) prefix_sum = [0.0] * (n + 1) prefix_sum_sqr = [0.0] * (n + 1) for i in range(1, n + 1): prefix_sum[i] = prefix_sum[i - 1] + f[i - 1] prefix_sum_sqr[i] = prefix_sum_sqr[i - 1] + f[i - 1] ** 2 def get_best_sse(l, r): num = r - l + 1 s_sqr = (prefix_sum[r] - prefix_sum[l - 1]) ** 2 ss = prefix_sum_sqr[r] - prefix_sum_sqr[l - 1] return ss - s_sqr / num dp_curr = [1e100] * (n + 1) dp_prev = [1e100] * (n + 1) dp_prev[0] = 0.0 for num_segments in range(1, k + 1): dp_curr[num_segments] = 0.0 for num_covered in range(num_segments + 1, n + 1): dp_curr[num_covered] = 1e100 for num_covered_previously in range(num_segments - 1, num_covered): dp_curr[num_covered] = min(dp_curr[num_covered], dp_prev[num_covered_previously] + get_best_sse(num_covered_previously + 1, num_covered)) dp_curr, dp_prev = dp_prev, dp_curr print(dp_prev[n]) 

التنبؤ بنقرات المستخدم

حالة

واحدة من أهم الإشارات لنظام التوصية هو سلوك المستخدم. , .

..

2 : (train.csv) (test.csv). , . :

— sample_id — id ,
— item — id ,
— publisher — id ,
— user — id ,
topic_i, weight_i — id i- ( 0 100) (i = 0, 1, 2, 3, 4),
— target — (1 — , 0 — ). .

.

, item, publisher, user, topic .

csv-, : sample_id target, sample_id — id , target — . test.csv. sample_id ( , test.csv). target 0 1.

logloss.

150 . logloss :

$$

$$\begin{equation*} score = \begin{cases} 0 &\text{, logloss > 0.5}\\ min(150,(200 * (0.5 - logloss))^2) &\text{, logloss ≤ 0.5} \end{cases} \end{equation*}$$

logloss . 2 , logloss 4 .

, . . , (, , , ) , — , - , .

, 100 ( 150).

— CatBoost . CatBoost ( ), . , . , -: $$$(\frac{\ \ \ }{\ })$ , , , , - ( ).

. , - , : FM (Factorization Machines) FFM (Field-aware Factorization Machines).

---

, ML- .