طبقة تلافيفية: الإلتواء السريع وفقًا لطريقة شموئيل فينوغراد

مقدمة

هذه المقالة هي سلسلة من المقالات التي تصف الخوارزميات الأساسية.
Synet هو إطار لإطلاق شبكات عصبية مدربة مسبقًا على وحدة المعالجة المركزية.

في مقال سابق ، وصفت الأساليب القائمة على الضرب المصفوفة. هذه الطرق بأقل جهد ممكن يمكن أن تحقق في كثير من الحالات أكثر من 80٪ من الحد الأقصى النظري. يبدو ، حسنًا ، أين يمكننا تحسينه؟ اتضح أنك تستطيع! هناك طرق رياضية يمكن أن تقلل من عدد العمليات المطلوبة للالتفاف. سوف نتعرف على إحدى هذه الطرق ، خوارزمية الالتواء باستخدام طريقة Vinograd ، في هذه المقالة.


شموئيل فينوغراد 1936.01.04 - 2019.03.25 - عالم كمبيوتر إسرائيلي وأمريكي بارز ، مصمم لوغاريتمات الضرب السريع للمصفوفة ، الإلتفاف وتحويل فورييه.

قليلا من الرياضيات

على الرغم من أنه في التعلم الآلي ، يتم استخدام التلفيفات ذات النواة المربعة في أغلب الأحيان ، من أجل تبسيط العرض التقديمي ، سننظر أولاً في الحالة أحادية البعد. لنفترض أن لدينا صورة أحادية الأبعاد للإدخال $$$1 \ times4$ :

$$

$$d = \ تبدأ {bmatrix} d_0 & d_1 & d_2 & d_3 \ end {bmatrix} ^ T ،$$

وحجم مرشح $$$1 \ times3$ :

$$

$$g = \ تبدأ {bmatrix} g_0 & g_1 & g_2 \ end {bmatrix} ^ T ،$$

بعد ذلك ستكون نتيجة الإلتواء:

$$

$$F (2،3) = \ تبدأ {bmatrix} d_0 g_0 + d_1 g_1 + d_2 g_2 \\ d_1 g_0 + d_2 g_1 + d_3 g_2 \ end {bmatrix}.$$

سيتم إعادة كتابة هذه التعبيرات بشكل مريح في شكل مصفوفة:

$$

$$F (2،3) = \ start {bmatrix} d_0 & d_1 & d_2 \\ d_1 & d_2 & d_3 \ end {bmatrix} \ start {bmatrix} g_0 \\ g_1 \\ g_2 \ end {bmatrix} = \ start {bmatrix} d_0 g_0 + d_1 g_1 + d_2 g_2 \\ d_1 g_0 + d_2 g_1 + d_3 g_2 \ end {bmatrix} = \ تبدأ {bmatrix} m_1 + m_2 + m_3 \\ m_2 - m_3 - m_4 \ end {bmatrix} ، (1) دولا$$

حيث يتم استخدام الترميز:

$$

$$m_1 = (d_0-d_2) g_0، \\ m_2 = (d_1 + d_2) \ frac {g_0 + g_1 + g_2} {2}، \\ m_3 = (d_2-d_1) \ frac {g_0-g_1 + g_2} {2} ، \\ m_4 = (d_1-d_3) g_2.$$

للوهلة الأولى ، يبدو البديل الأخير بلا معنى إلى حد ما - من الواضح أن هناك المزيد من العمليات. لكن التعبيرات $$$\ frac {g_0 + g_1 + g_2} {2}$ و $$$\ frac {g_0-g_1 + g_2} {2}$ تحتاج فقط إلى حساب مرة واحدة. مع وضع ذلك في الاعتبار ، نحتاج إلى إجراء 4 عمليات للضرب فقط ، بينما في الصيغة الأصلية يجب أن يتم ذلك 6.
نعيد كتابة التعبير (1):

$$

$$F (2،3) = A ^ T [(G g) \ odot (B ^ T d)] ، (2)$$

حيث $$$\ odot$ يدل على الضرب بالعنصر ، ويستخدم الترميز التالي أيضًا:

$$

$$B ^ T = \ start {bmatrix} 1 & 0 & -1 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & -1 & 1 & 0 \\ 0 & 1 & 0 & -1 \ end { bmatrix}، (3) \\ G = \ تبدأ {bmatrix} 1 & 0 & 0 \\ \ frac {1} {2} & \ frac {1} {2} & \ frac {1} {2} \\ \ frac {1} {2} & - \ frac {1} {2} & \ frac {1} {2} \\ 0 & 0 & 1 \ end {bmatrix}، (4) \\ A ^ T = \ تبدأ {bmatrix} 1 & 1 & 1 & 0 \\ 0 & 1 & -1 & -1 \ end {bmatrix}. (5) دولا$$

يمكن تعميم التعبير (2) على الحالة ثنائية الأبعاد:

$$

$$F (2 \ times2،3 \ times3) = A ^ T \ bigg [[G g G ^ T] \ odot [B ^ T d B] \ bigg] A. (6)$$

العدد المطلوب من عمليات الضرب ل $$$F (2 \ times2،3 \ times3)$ يتقلص من $$$2 \ times2 \ times3 \ times3 = 36$ إلى $$ . وبالتالي نحصل على المكسب الحسابي في $$$\ frac {36} {16} = 2.25 دولا$ مرات. إذا قمت بالتخيل ، فعندئذ في الواقع ، بدلاً من حساب منفصل الإلتواء لكل نقطة في الصورة ، سنقوم بحسابها على الفور لحجم من الحجم $$$2 \ times2$ :

في أي حال ، لالتواء مع النافذة $$$r \ times s$ وحجم الكتلة $$$م \ مرات ن$ عدد الضرب المطلوب سيكون

$$

$$count = (m + r - 1) \ times (n + s - 1)، (7)$$

ويتم وصف الكسب بالصيغة:

$$

$$k = \ frac {m \ times n \ times r \ times s} {(m + r - 1) \ times (n + s - 1)}. (8) دولا$$

في الحد الأقصى ، كبيرة بما فيه الكفاية $$$م دولا$ و $$$ن$ لأي إلتواء ، عملية الضرب فقط بنقطة واحدة تكفي! لسوء الحظ ، تؤدي الزيادة في حجم الكتلة إلى زيادة سريعة في مقدار الحمل $$$B ^ T d B$ وعطلة نهاية الاسبوع $$$A ^ T [...]$ الصور ، لذلك في الممارسة العملية عادة لا تستخدم حجم كتلة أكبر من $$$4 \ times4$ .

مثال التنفيذ

من أجل التنفيذ العملي لخوارزمية Vinograd ، أود أن أفكر في أبسط الحالات - الالتحام مع النواة $$ لكتلة $$$2 \ times2$ . لزيادة تبسيط العرض التقديمي ، سنفترض أيضًا عدم وجود حشوة لصورة الإدخال ، وأن أحجام الصور المدخلة والمخرجات هي مضاعفات 2.

سيبدو تطبيق الالتفاف المستند إلى ضرب المصفوفة:

float relu(float value) { return value > 0 ? return value : 0; } void gemm_nn(int M, int N, int K, float alpha, const float * A, int lda, float beta, const float * B, int ldb, float * C, int ldc) { for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) { C[i*ldc + j] = beta; for (int k = 0; k < K; ++k) C[i*ldc + j] += alpha * A[i*lda + k] * B[k*ldb + j]; } } void im2col(const float * src, int srcC, int srcH, int srcW, int kernelY, int kernelX, float * buf) { int dstH = srcH - kernelY + 1; int dstW = srcW - kernelX + 1; for (int sc = 0; sc < srcC; ++sc) for (int ky = 0; ky < kernelY; ++ky) for (int kx = 0; kx < kernelX; ++kx) for (int dy = 0; dy < dstH; ++dy) for (int dx = 0; dx < dstW; ++dx) *buf++ = src[((b * srcC + sc)*srcH + dy + ky)*srcW + dx + kx]; } void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC, float * buf) { int dstH = srcH - kernelY + 1; int dstW = srcW - kernelX + 1; int M = dstC; int N = dstH * dstW; int K = srcC * kernelY * kernelX; for (int b = 0; b < batch; ++b) { im2col(src, srcC, srcH, srcW, kernelY, kernelX, buf); gemm_nn(M, N, K, 1, weight, K, 0, buf, N, dst, N)); for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) dst[i*N+ j] = relu(dst[i*N + j] + bias[i]); src += srcC*srcH*srcW; dst += dstC*dstH*dstW; } } 

يجب على من يريد أن يفهم بالتفصيل ما يحدث هنا أن يلجأ إلى مقالتي السابقة . يتم الحصول على التنفيذ الحالي من التطبيق السابق ، إذا وضعنا:

 strideY = strideX = dilationY = dilationX = group = 1, padY = padX = padH = padW = 0. 

خوارزمية الإلتفاف المعدلة

أعطي هنا مرة أخرى الصيغة (6):

$$

$$F (2 \ times2،3 \ times3) = A ^ T \ bigg [[G g G ^ T] \ odot [B ^ T d B] \ bigg] A.$$

إذا قمت بالتبديل من حجم صورة الإخراج $$$2 \ times2$ إلى صورة ذات حجم تعسفي ، ثم سيتعين علينا تقسيمها إلى كتل من الحجم $$$2 \ times2$ . لكل كتلة ، سيتم تكوين صورة إدخال $$$(2 + 3 - 1) \ مرة (2 + 3 - 1) = 16 دولا$ القيم التي تم تضمينها في 16 تحويلها $$$B ^ T d B$ الصور المدخلة انخفاض في حجم نصف. ثم ، يتم ضرب كل من هذه المصفوفات 16 بالمصفوفة المقابلة للأوزان المحولة $$$G g G ^ T$ . يتم تحويل 16 المصفوفات الناتجة إلى صورة الإخراج $$$A ^ T \ bigg [... \ bigg] A$ . أدناه يتم رسم هذه العملية في الرسم البياني:



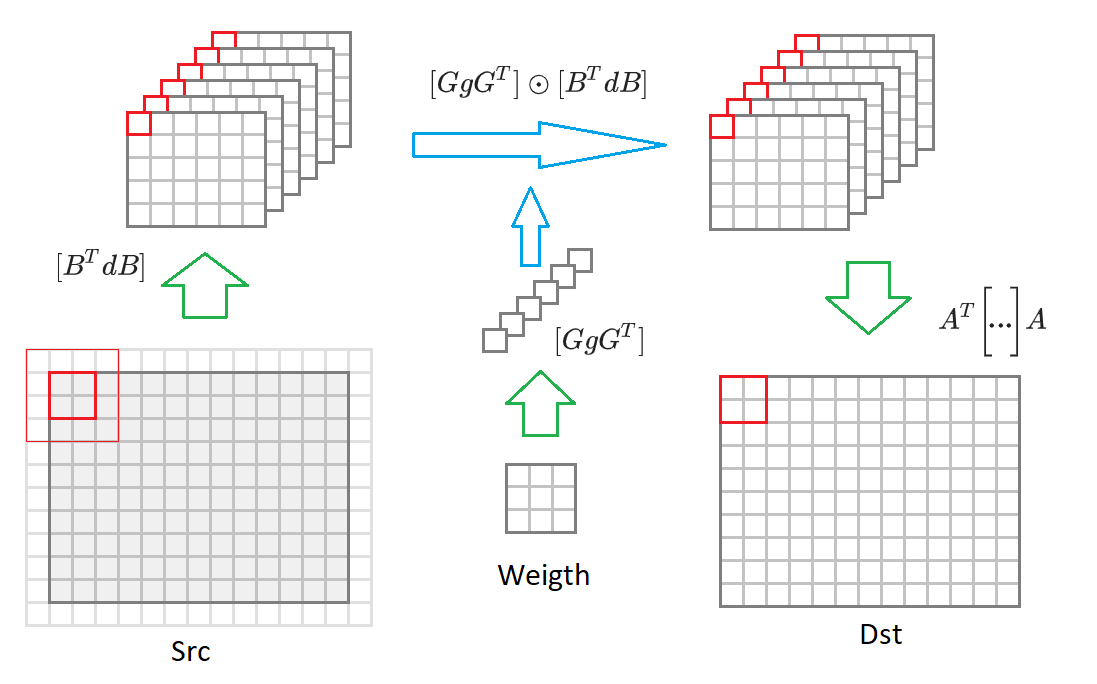
في ضوء هذه التعليقات ، تأخذ خوارزمية الالتواء النموذج:

 void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC, float * buf) { const int block = 2, kernel = 3; int count = (block + kernel - 1)*(block + kernel - 1); // 16 int dstH = srcH - kernelY + 1; int dstW = srcW - kernelX + 1; int tileH = dstH / block; int tileW = dstW / block; int sizeW = srcC * dstC; int sizeS = srcC * tileH * tileW; int sizeD = dstC * tileH * tileW; int M = dstC; int N = tileH * tileW; int K = srcC; float * bufW = buf; float * bufS = bufW + sizeW*count; float * bufD = bufS + sizeS*count; set_filter(weight, sizeW, bufW); for (int b = 0; b < batch; ++b) { set_input(src, srcC, srcH, srcW, bufS, sizeS); for (int i = 0; i < count; ++i) gemm_nn(M, N, K, 1, bufW + i * sizeW, K, bufS + i * sizeS, N, 0, bufD + i * sizeD, N)); set_output(bufD, sizeD, dst, dstC, dstH, dstW); for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) dst[i*N+ j] = relu(dst[i*N + j] + bias[i]); src += srcC*srcH*srcW; dst += dstC*dstH*dstW; } } 

عدد العمليات المطلوبة دون الأخذ في الاعتبار تحويلات صورة المدخلات والمخرجات: ~ srcC * dstC * dstH * dstW * count . بعد ذلك ، نقوم بوصف الخوارزميات لتحويل الأوزان وإدخال الصور وإخراجها.

تحويل المقاييس التلافيفية

كما يتضح من التعبير (6) ، يجب إجراء التحويل التالي على أوزان الالتواء: $$$G g G ^ T$ اين المصفوفة $$$G$ المعرفة في التعبير (4). سيبدو رمز هذا التحويل كما يلي:

 void set_filter(const float * src, int size, float * dst) { for (int i = 0; i < size; i += 1, src += 9, dst += 1) { dst[0 * size] = src[0]; dst[1 * size] = (src[0] + src[2] + src[1])/2; dst[2 * size] = (src[0] + src[2] - src[1])/2; dst[3 * size] = src[2]; dst[4 * size] = (src[0] + src[6] + src[3])/2; dst[5 * size] = ((src[0] + src[6] + src[3]) + (src[2] + src[8] + src[5]) + (src[1] + src[7] + src[4]))/4; dst[6 * size] = ((src[0] + src[6] + src[3]) + (src[2] + src[8] + src[5]) - (src[1] + src[7] + src[4]))/4; dst[7 * size] = (src[2] + src[8] + src[5])/2; dst[8 * size] = (src[0] + src[6] - src[3])/2; dst[9 * size] = ((src[0] + src[6] - src[3]) + (src[2] + src[8] - src[5]) + (src[1] + src[7] - src[4]))/4; dst[10 * size] = ((src[0] + src[6] - src[3]) + (src[2] + src[8] - src[5]) - (src[1] + src[7] - src[4]))/4; dst[11 * size] = (src[2] + src[8] - src[5])/2; dst[12 * size] = src[6]; dst[13 * size] = (src[6] + src[8] + src[7])/2; dst[14 * size] = (src[6] + src[8] - src[7])/2; dst[15 * size] = src[8]; } } 

لحسن الحظ ، يجب إجراء هذا التحويل مرة واحدة فقط. لذلك ، لا يؤثر على الأداء النهائي.

إدخال صورة التحويل

كما يتضح من التعبير (6) ، يجب إجراء التحويل التالي على صورة الإدخال: $$$B ^ T d B$ اين المصفوفة $$$B ^ T$ المعرفة في التعبير (3). سيبدو رمز هذا التحويل كما يلي:

 void set_input(const float * src, int srcC, int srcH, int srcW, float * dst, int size) { int dstH = srcH - 2; int dstW = srcW - 2; for (int c = 0; c < srcC; ++c) { for (int row = 0; row < dstH; row += 2) { for (int col = 0; col < dstW; col += 2) { float tmp[16]; for (int r = 0; r < 4; ++r) for (int c = c; c < 4; ++c) tmp[r * 4 + c] = src[(row + r) * srcW + col + c]; dst[0 * size] = (tmp[0] - tmp[8]) - (tmp[2] - tmp[10]); dst[1 * size] = (tmp[1] - tmp[9]) + (tmp[2] - tmp[10]); dst[2 * size] = (tmp[2] - tmp[10]) - (tmp[1] - tmp[9]); dst[3 * size] = (tmp[1] - tmp[9]) - (tmp[3] - tmp[11]); dst[4 * size] = (tmp[4] + tmp[8]) - (tmp[6] + tmp[10]); dst[5 * size] = (tmp[5] + tmp[9]) + (tmp[6] + tmp[10]); dst[6 * size] = (tmp[6] + tmp[10]) - (tmp[5] + tmp[9]); dst[7 * size] = (tmp[5] + tmp[9]) - (tmp[7] + tmp[11]); dst[8 * size] = (tmp[8] - tmp[4]) - (tmp[10] - tmp[6]); dst[9 * size] = (tmp[9] - tmp[5]) + (tmp[10] - tmp[6]); dst[10 * size] = (tmp[10] - tmp[6]) - (tmp[9] - tmp[5]); dst[11 * size] = (tmp[9] - tmp[5]) - (tmp[11] - tmp[7]); dst[12 * size] = (tmp[4] - tmp[12]) - (tmp[6] - tmp[14]); dst[13 * size] = (tmp[5] - tmp[13]) + (tmp[6] - tmp[14]); dst[14 * size] = (tmp[6] - tmp[14]) - (tmp[5] - tmp[13]); dst[15 * size] = (tmp[5] - tmp[13]) - (tmp[7] - tmp[15]); dst++; } } src += srcW * srcH; } } 

عدد العمليات المطلوبة لهذا التحويل هو: ~ srcH * srcW * srcC * count .

تحويل صورة الناتج

كما يتضح من التعبير (6) ، يجب إجراء التحويل التالي على صورة الإخراج: $$$A ^ T [...]$ اين المصفوفة $$$B ^ T$ المعرفة في التعبير (5). سيبدو رمز هذا التحويل كما يلي:

 void set_output(const float * src, int size, float * dst, int dstC, int dstH, int dstW) { for (int c = 0; c < dstC; ++c) { for (int row = 0; row < dstH; row += 2) { for (int col = 0; col < dstW; col += 2) { float tmp[8]; tmp[0] = src[0 * size] + src[1 * size] + src[2 * size]; tmp[1] = src[1 * size] - src[2 * size] - src[3 * size]; tmp[2] = src[4 * size] + src[5 * size] + src[6 * size]; tmp[3] = src[5 * size] - src[6 * size] - src[7 * size]; tmp[4] = src[8 * size] + src[9 * size] + src[10 * size]; tmp[5] = src[9 * size] - src[10 * size] - src[11 * size]; tmp[6] = src[12 * size] + src[13 * size] + src[14 * size]; tmp[7] = src[13 * size] - src[14 * size] - src[15 * size]; dst[col + 0] = tmp[0] + tmp[2] + tmp[4]; dst[col + 1] = tmp[1] + tmp[3] + tmp[5]; dst[dstW + col + 0] = tmp[2] - tmp[4] - tmp[6]; dst[dstW + col + 1] = tmp[3] - tmp[5] - tmp[7]; src++; } dst += 2*dstW; } } } 

عدد العمليات المطلوبة لهذا التحويل هو: ~ dstH * dstW * dstC * count .

ميزات التنفيذ العملي

في المثال أعلاه ، وصفنا خوارزمية Vinohrad لكتلة من الحجم $$$2 \ times2$ . في الممارسة العملية ، غالبًا ما يتم استخدام إصدار أكثر تقدماً من الخوارزمية: $$$F (4 \ times4،3 \ times3)$ . في هذه الحالة ، سيكون حجم الكتلة $$$4 \ times4$ ، وعدد المصفوفات المحولة هو 36. وسيصل الكسب الحسابي ، وفقًا للصيغة (8) ، إلى 4 . المخطط العام للخوارزمية هو نفسه ، فقط مصفوفة خوارزميات التحويل تختلف.

هناك مشروع صغير على جيثب يسمح لك بحساب هذه المصفوفات مع معاملات لحجم النواة الإلتواء التعسفي وحجم الكتلة.

قدمنا ​​متغيرًا من خوارزمية Vinograd لتنسيق صورة NCHW ، ولكن يمكن تنفيذ الخوارزمية بطريقة مماثلة لتنسيق NHWC (تحدثت بمزيد من التفاصيل حول تنسيقات الصور هذه في المقالة السابقة .

على الرغم من وجود تحويلات إضافية ، فإن العبء الحسابي الرئيسي في خوارزمية Vinograd (مع تطبيقه المختص ، بالطبع) لا يزال يكمن في ضرب المصفوفة. لحسن الحظ ، هذه عملية قياسية ويتم تنفيذها بشكل فعال في العديد من المكتبات.

يمكن العثور على وظائف التحويل المحسّنة لمنصات مختلفة لخوارزمية Vinohrad هنا .

إيجابيات وسلبيات خوارزمية العنب

أولاً ، بالطبع ، الايجابيات:

• تسمح الخوارزمية عدة مرات (في أغلب الأحيان 2-3 مرات) بتسريع حساب الإلتواء. وبالتالي ، من الممكن حساب الإلتواء بشكل أسرع من الحد "النظري".
• تعتمد الخوارزمية في تنفيذها على خوارزمية الضرب المصفوفة القياسية.
• يمكن تنفيذه لتنسيقات الصور المدخلة المختلفة: NCHW ، NHWC .
• حجم المخزن المؤقت لتخزين القيم المتوسطة أصغر من ذلك المطلوب لخوارزمية الضرب المصفوفة.

حسنا وأين دون السلبيات:

• تتطلب الخوارزمية تنفيذ منفصل لوظائف التحويل لكل حجم نواة الالتواء ، وكذلك لكل حجم كتلة. ربما هذا هو أحد الأسباب الرئيسية لأنه يتم تطبيقه في كل مكان تقريبًا فقط من أجل الالتفاف على النواة. $$ .
• مع نمو حجم الكتلة ، يزداد تعقيد تنفيذ وظائف التحويل بسرعة. لذلك ، لا توجد تطبيقات عمليًا بحجم كتلة أكبر من $$$4 \ times4$ .
• تفرض الخوارزمية قيودًا صارمة على معلمات الالتواء strideY = strideY = dilationY = dilationX = group = 1 . على الرغم من أنه من الناحية النظرية ، من الممكن تطبيق الخوارزمية عند انتهاك هذه القيود ، إلا أنها في الواقع صغيرة التطبيق بسبب انخفاض الكفاءة.
• تتناقص كفاءة الخوارزمية إذا كان عدد قنوات الإدخال أو الإخراج في الصورة صغيرًا (ويعزى ذلك إلى تكلفة تحويل صور المدخلات والمخرجات).
• تتناقص كفاءة الخوارزمية بالنسبة لأحجام صغيرة من الصور المدخلة (المصفوفات الناتجة من صورة الإدخال صغيرة جدًا ، وتصبح خوارزمية مضاعفة المصفوفة القياسية غير فعالة بالنسبة لهم).

النتائج

يمكن لطريقة حساب الإلتفاف بناءً على خوارزمية Vinograd زيادة الكفاءة الحسابية بشكل ملحوظ مقارنة بالطريقة القائمة على الضرب البسيط للمصفوفة. لسوء الحظ ، فإنه ليس عالميًا وصعب التنفيذ. بالنسبة لعدد من الحالات الخاصة ، توجد طرق أسرع ، أوصي وصفها بتأجيل المقالات التالية من هذه السلسلة . في انتظار ردود الفعل والتعليقات من القراء. آمل أن تكونوا مهتمين!

ملاحظة: يتم تنفيذ هذا النهج وغيره من الأساليب في إطار Convolution Framework كجزء من مكتبة Simd .
يرتكز هذا الإطار على Synet ، وهو إطار لتشغيل الشبكات العصبية المدربة مسبقًا على وحدة المعالجة المركزية.