كتب بواسطة rakf
كجزء من Summer of Hack 2019 في Digital Security ، تعاملت مع هجوم قوي وعملت مع ChipWhisperer.
ما هذا
تحليل الطاقة هو نوع من الهجوم من خلال قنوات الطرف الثالث. بمعنى ، الهجمات التي تستخدم المعلومات التي تظهر كنتيجة للتنفيذ الفعلي للنظام.
ما المعلومات التي قد تكون مفيدة للمهاجمين:
- وقت تحويل التشفير ؛
- استهلاك الطاقة ؛
- المجالات الكهرومغناطيسية ؛
- الضوضاء الخ
يعتبر هجوم الطاقة الأكثر عالمية.
لماذا تعمل؟
تعتمد المعالجات الدقيقة ووحدات التحكم الدقيقة وذاكرة الوصول العشوائي والعديد من الدوائر المنطقية الأخرى على تقنية CMOS. يتكون استهلاك طاقة دوائر CMOS من مكونين: ثابت وديناميكي. استهلاك الطاقة الثابت صغير جدًا ، وهو أحد أسباب احتكار التكنولوجيا. الطاقة الديناميكية ناتجة عن تبديل الترانزستورات وتعتمد على البيانات المعالجة والعمليات المنجزة. نظرًا لأن المكون الثابت ثابت بشكل أساسي ، فإن التغيير في إجمالي الطاقة يرجع بشكل حصري إلى القدرة الديناميكية ، وبالتالي ، يمكن استخدام إجمالي استهلاك الطاقة للتحليل.
أدوات
ChipWhisperer ، استخدمت الإصدار المكون من جزأين:

ChipWhisperer عبارة عن مجموعة أدوات مفتوحة المصدر للبحث في أمان الأجهزة المدمجة. لأنها تتيح تحليل الطاقة والهجمات القائمة على الخطأ.
سوف رسوم تكلفة 250 دولار. يضعه المطورون كحل ثوري ، لأن هذه المجمعات ، وفقًا للمبدعين ، تكلف 30 ألف دولار. يتكون الجهاز من لوحين: لوحة الهدف والتقاط.
هناك إصدارات أخرى ، مع مزاياها (ولكن أيضًا بتكلفة كبيرة) ، يمكنك أيضًا شراء مختلف اللوحات المستهدفة وبطاقات التوسيع والتحقيق لإجراء تحليل كامل للأجهزة الخاصة بك واستخدام ChipWhisperer فقط للإزالة.
ChipWhisperer لديه ويكي ممتازة ، ومختبرات تطوير صغيرة ، وحتى الإصدار الخامس قاموا بعمل وثائق API جيدة. تتم إزالة المسارات من الجهاز المتصل باستخدام برامجهم وتسجيلها كصفيف NumPy.
تحتاج أولاً إلى كتابة البرنامج الثابت للجهاز الهدف. كجزء من المختبر ، تعتبر الأصفار AES ، DES ، TEA. بالنسبة لهم ، هناك بالفعل إعدادات وإعدادات ثابتة جاهزة لإزالة الآثار (عدد العينات التي يجب أخذها ، الإزاحة ، تردد ADC ، إلخ). لإعدادات البحث المستقلة ، يجب تحديدها تجريبياً.
كما ذكر أعلاه ، يمكنك إثارة فشل اللوحة الهدف: التسبب في خلل في إشارة الساعة ، وتخطي التعليمات واستخراج المعلومات السرية.
في المجمعات الكبيرة ، يستخدم الذبذبات لتتبع المسارات.
تحليل
هناك العديد من طرق التحليل الأساسية:
- تحليل الطاقة البسيطة (SPA) ؛
- تحليل القوة التفاضلية (DPA) ؛
- تحليل ارتباط الطاقة (CPA).
يتضمن تحليل الطاقة البسيط تحليلًا مرئيًا للرسم البياني للطاقة. على سبيل المثال ، يمكن الحصول على كلمة المرور حرفًا واحدًا في كل مرة من خلال ملاحظة ملف تعريف الطاقة عند إدخال الحرف الصحيح ومقارنته بالحرف الخطأ.
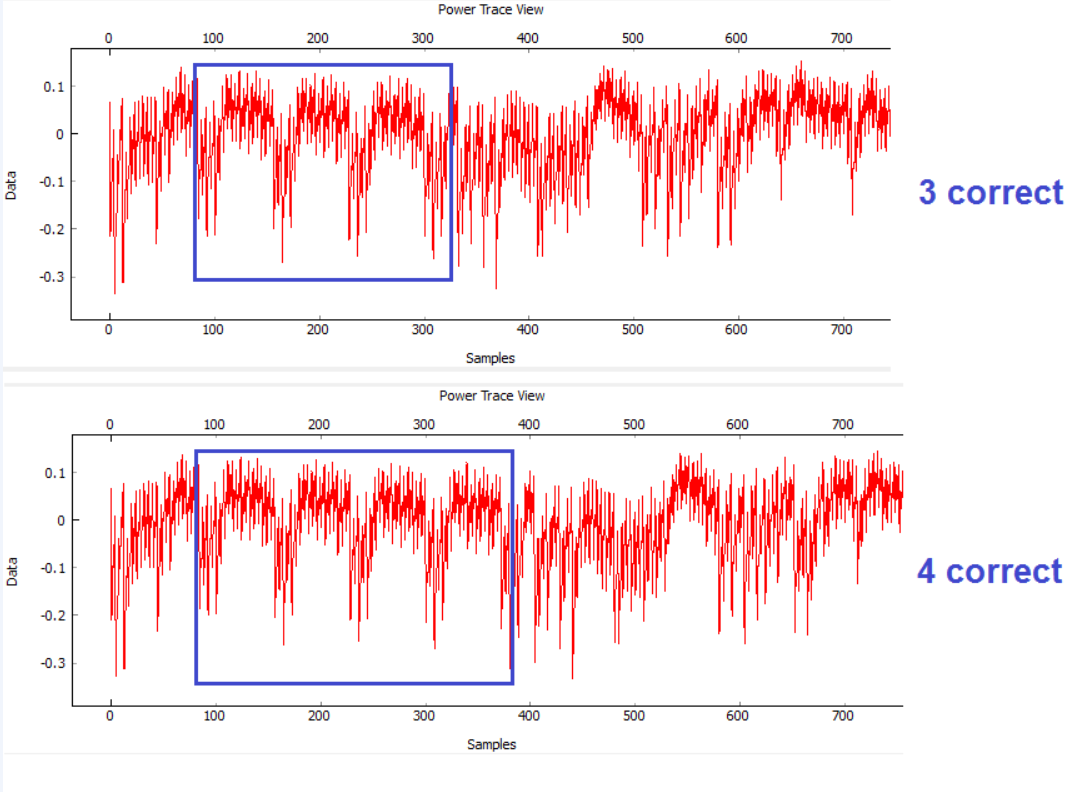
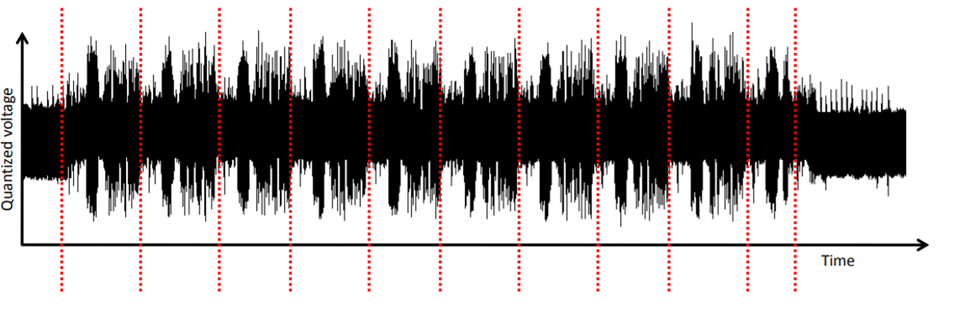
أو يمكنك رؤية جولات التشفير على المسارات. لا يكفي الحصول على البيانات ، ولكن يمكن افتراض الخوارزمية التي يتم تنفيذها. يوضح الشكل بوضوح 10 جولات من AES.
يعد التحليل التفاضلي (DPA) أكثر فعالية من التحليل البسيط ، حيث يعتمد تحليل DPA على طرق التحليل الإحصائي لاكتشاف الاختلافات في آثار الطاقة. ومع ذلك ، فإن أداة فعالة للغاية "لفتح" المفتاح ستتطلب عددًا كبيرًا من المسارات. لم أستخدم هذه الطريقة للتحليل ، لكن في النهاية سأقدم بعض الروابط إلى المصادر التي تم وصفها جيدًا.
أساس تحليل الارتباط هو جهاز إحصائي لتحديد مفتاح التشفير السري. في بعض الأحيان يتم عزله في نوع منفصل ، يشار إليه أحيانًا باسم DPA. هذه الطريقة تتطلب آثار أقل من DPA ، لقد استخدمتها لتحليل الطاقة. سوف أخبركم المزيد حول هذا الموضوع.
المهمة الرئيسية هي بناء نموذج دقيق لاستهلاك الطاقة للجهاز قيد الدراسة. إذا تم بناء نموذج دقيق ، فهناك ارتباط واضح بين القيمة المتوقعة والقيمة الفعلية.
واحد من نماذج الطاقة التي يمكن استخدامها هو نموذج الوزن هامينغ. وزن Hamming هو عدد القيم غير الصفرية في التمثيل الثنائي. يفترض هذا النموذج أن عدد وحدات البت المحددة في السجل سوف يرتبط بالطاقة التي يستهلكها الجهاز. يستخدم وزن هامينغ نفسه فيما بعد كوحدة طاقة تقليدية. يستخدم نموذج مسافة Hamming أيضًا - عدد البتات المختلفة في قيمتين.
لمقارنة نموذج وزن Hamming واستهلاك الطاقة الحقيقي ، يتم استخدام معامل Pearson الخطي. يُظهر الاعتماد الخطي لكمية واحدة على أخرى. باستخدام نموذج تم إنشاؤه بشكل صحيح ، يميل هذا المعامل إلى 1.
تتكون خوارزمية CPA المعممة من الخطوات الرئيسية التالية:
- إزالة استهلاك الطاقة عند تحويل الرسائل على مفتاح غير معروف ؛
- نبني نموذجًا لاستهلاك الطاقة للرقاقة عند تحويل الرسائل نفسها على جميع المتغيرات المحتملة للكتلة الفرعية الرئيسية (256 خيارًا لكل بايت) ؛
- نجد معامل الارتباط الخطي لاستهلاك الطاقة المحاكي والحقيقي. في حالة وجود مفتاح حقيقي ، يميل المعامل إلى 1 ؛
- يتم تكرار الخوارزمية للكتل الفرعية الرئيسية المتبقية.
نتيجة لذلك ، يتم استعادة المفتاح بالتتابع ، في أجزاء صغيرة. إذا هاجمنا بايت واحد من المفتاح في وقت واحد ، فإننا نستخدم 2 8 محاولات لكل مفتاح. على سبيل المثال ، إذا اخترت AES - 128 ، فسيكون العدد الإجمالي لمحاولات 16 بايت من المفتاح هو 2 12 ، وهو أفضل بكثير من ضرب 2 128 .
تحليل الصهارة التشفير
الصهارة هو رمز تم تعريفه في GOST R 34.12-2015 ، في الواقع نفس GOST 28147-89 ، فقط في الملف الشخصي. تمر الكتلة المشفرة خلال 32 جولة تحدث فيها بعض التحويلات. يتكون المفتاح من 256 بت ، كل مفتاح دائري جزء من الأصل.
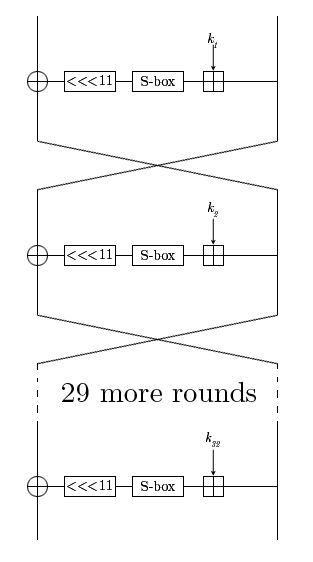
سنقوم بتحليل البيانات التي تم الحصول عليها باستخدام طريقة اتفاق السلام الشامل.
أولاً ، تحتاج إلى اختيار قيمة وسيطة للخوارزمية ، والتي تعتمد على البيانات المعروفة وجزء صغير من المفتاح ويمكن حسابها بتحويلات بسيطة. عادةً ما تكون هذه القيمة هي إخراج S-box (يحتوي Magma الآن على جدول بديل واحد ، لذلك من الأسهل تنفيذ مثل هذه الهجمات) من الأولى (النصوص المفتوحة معروفة) أو الجولة الأخيرة (تُعرف النصوص المشفرة).
لقد بحثت في مفتاح يحتوي على نصوص مفتوحة معروفة ، وبالتالي سيتم النظر في هذا الخيار. في خوارزمية الصهارة ، على عكس DES ، AES ، تحدث إضافة كتلة 32 بت مع مفتاح مستدير المعيار 2 32 ، لذلك ، من الأفضل أن تبدأ التحليل من آخر مخرجات S-box ، لأن إضافة أعلى القيم لا تؤثر على الأصغر سناً. نحن نعتبر إخراج كل صندوق S: أول 8 ، ثم يعطى 8 ، 7 وهكذا حتى الأول. تم تنفيذ إزالة المسار على متحكم 8 بت ، ويمكننا أن نفترض أنها عملت مع صناديق S مزدوجة. لذلك ، سأهاجم على الفور بواسطة 1 بايت.
حساب نموذج الطاقة لآخر بايت رئيسي:
for kguess in range(0, 256):
حيث تقوم دالة التسرب ببساطة بإرجاع إخراج S-box للبايت الأخير.
نحسب معامل بيرسون الخطي للقيم المحاكاة والحقيقية وفقًا للصيغة:
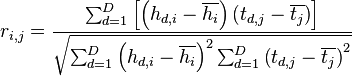
cpaoutput = [0]*256 maxcpa = [0]*256
عند اختيار مفتاح فرعي حقيقي ، سيكون لمعامل الارتباط زيادة ملحوظة:
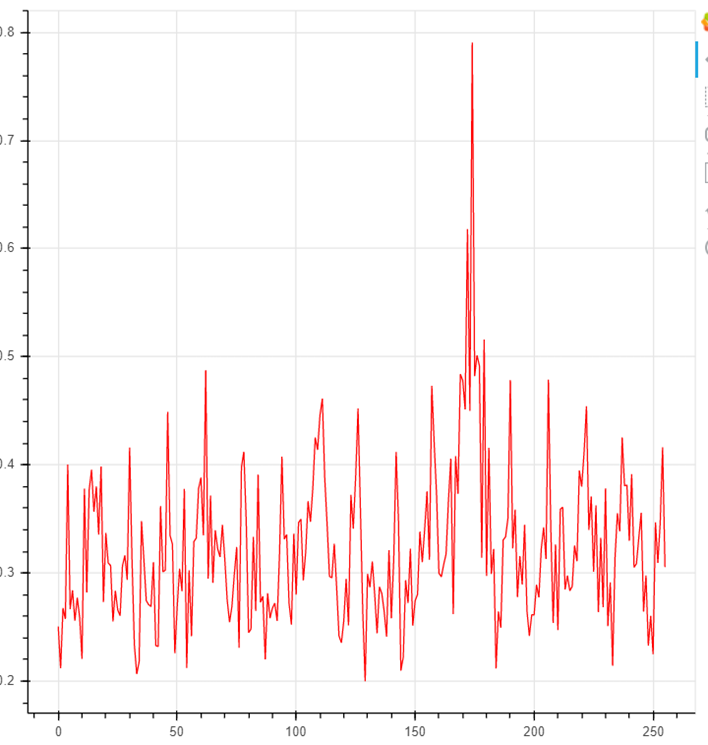
وبالتالي ، يتم تحليل كل بايت من مفتاح الجولة.
for bnum in range(0, 4): cpaoutput = [0]*256 maxcpa = [0]*256 for kguess in range(0, 256): best_round_key = kguess << (bnum * 8) | best_round ...
بالنظر إلى مفتاح الجولة الأولى ، يمكننا حساب مفاتيح الجولة 2 واللاحقة بنفس الطريقة. يمكن الحصول على مفتاح Magma الكامل من خلال إخراج 8 مفاتيح مستديرة.
في عملية حل هذه المشكلة ، تنشأ عدة فروق دقيقة. على عكس AES ، DES ، الأصفار Grasshopper ، إضافة مفتاح مستدير غير ظاهر يحدث في المعامل 2 32 . تؤثر إضافة وحدات البت المنخفضة على النسبة العالية ، على عكس XORa. عند حساب كل مفتاح فرعي لاحق ، يجب عليك مراعاة نتائج الماضي. وبالمثل مع مفاتيح الجولة. البيانات حساسة للغاية. إذا تم حساب إحدى القيم بشكل غير صحيح ، فسيكون الحساب الإضافي للمفتاح بأكمله غير صحيح.
تجدر الإشارة أيضًا إلى أنه من الصعب للغاية الآن العثور على شريحة بها بنية ذات أربعة بتات: معظم الشرائح بها ثمانية بتات. بالطبع ، هناك شرائح تشفير متخصصة مصممة لخوارزمية تحويل أمان معينة (أو عدة خوارزميات) ولديها البنية الأكثر كفاءة.
لتنفيذ تشفير DES ، يمكن أن يكون لمعالج التشفير هذا بنية من ستة بتات لـ Magma - واحدة بأربعة بت ، والتي تسمح بمعالجة كل S-box بشكل منفصل. جهازي المستهدف هو 8 بت ، وفي حالة "الصهارة" ، سيتم إجراء التحويل على ثماني بتات في طريقة واحدة ، أي سيحدث الاستبدال على 2 S-box ، وسيتم النظر في استهلاك الطاقة لمدة 2 S-box. إذا تطابق أحد الصناديق S ، كبير أو صغير ، مع المفتاح الحقيقي ، والآخر غير متطابق ، فقد تحدث رشقات ارتباط عالية.
بالنظر إلى كل ما سبق ، في الناتج لدينا النص التالي لتحليل مسارات استهلاك الطاقة لشفرات الصهارة:
بيثون النصي import numpy as np path = r'C:\Users\user\chipwhisperer\projects\gost_10000_2_data\traces\2019.08.11-19.53.25_' traces = np.load(path + 'traces.npy') text = np.load(path + 'textin.npy') keys = np.load(path + 'keylist.npy') HW = [bin(n).count("1") for n in range(0,256)] SBOXES = {"Gost28147_tc26_ParamZ": ( (12, 4, 6, 2, 10, 5, 11, 9, 14, 8, 13, 7, 0, 3, 15, 1), (6, 8, 2, 3, 9, 10, 5, 12, 1, 14, 4, 7, 11, 13, 0, 15), (11, 3, 5, 8, 2, 15, 10, 13, 14, 1, 7, 4, 12, 9, 6, 0), (12, 8, 2, 1, 13, 4, 15, 6, 7, 0, 10, 5, 3, 14, 9, 11), (7, 15, 5, 10, 8, 1, 6, 13, 0, 9, 3, 14, 11, 4, 2, 12), (5, 13, 15, 6, 9, 2, 12, 10, 11, 7, 8, 1, 4, 3, 14, 0), (8, 14, 2, 5, 6, 9, 1, 12, 15, 4, 11, 0, 13, 10, 3, 7), (1, 7, 14, 13, 0, 5, 8, 3, 4, 15, 10, 6, 9, 12, 11, 2), )} def _K(s, _in): """ S-box substitution :param s: S-box :param _in: 32-bit word :returns: substituted 32-bit word """ return ( (s[0][(_in >> 0) & 0x0F] << 0) + (s[1][(_in >> 4) & 0x0F] << 4) + (s[2][(_in >> 8) & 0x0F] << 8) + (s[3][(_in >> 12) & 0x0F] << 12) + (s[4][(_in >> 16) & 0x0F] << 16) + (s[5][(_in >> 20) & 0x0F] << 20) + (s[6][(_in >> 24) & 0x0F] << 24) + (s[7][(_in >> 28) & 0x0F] << 28) ) def block2ns(data): """ Convert block to N1 and N2 integers """ data = bytearray(data) return ( data[7] | data[6] << 8 | data[5] << 16 | data[4] << 24, data[3] | data[2] << 8 | data[1] << 16 | data[0] << 24, ) def addmod(x, y, mod=2 ** 32): """ Modulo adding of two integers """ r = x + int(y) return r if r < mod else r - mod def _shift11(x): """ 11-bit cyclic shift """ return ((x << 11) & (2 ** 32 - 1)) | ((x >> (32 - 11)) & (2 ** 32 - 1)) def round(sbox, key, data, byte): s = SBOXES[sbox] _in = addmod(data, key) sbox_leak = _K(s, _in); return (sbox_leak >> (8 * byte)) & 0xFF def Feistel(sbox, key, data, nround): s = SBOXES[sbox] w = bytearray(key) x = [ w[3 + i * 4] | w[2 + i * 4] << 8 | w[1 + i * 4] << 16 | w[0 + i * 4] << 24 for i in range(8) ] n1, n2 = block2ns(data) for i in range(nround): n1, n2 = _shift11(_K(s, addmod(n1, x[i]))) ^ n2, n1 return n1 numtraces = len(traces) numpoint = np.shape(traces)[1] bestguess = [0]*32 round_data = [0] * numtraces for i in range(numtraces): round_data[i] = [0] * 8 for rnum in range(0, 8): best_round = 0 for tnum_r in range(numtraces): round_data[tnum_r][rnum] = Feistel("Gost28147_tc26_ParamZ", bestguess, text[tnum_r], rnum) for bnum in range(0, 4): cpaoutput = [0]*256 maxcpa = [0]*256 for kguess in range(0, 256):
مستودع جيثب للنتائج
النتائج
كجزء من الدراسة ، عملت مع ChipWhisperer. على الرغم من أنني لم أجرب كل الأدوات (على سبيل المثال ، التزوير) ، فإنني بالتأكيد أجد ChipWhisperer مفيدًا ، خاصة إذا كنت لا ترغب في شراء أجهزة خاصة باهظة الثمن.
بالنسبة لتحليل الشفرات الخاص بنا لاستهلاك الطاقة ، فهو أكثر مقاومة لهذا الهجوم من الأصفار الموصوفة أعلاه ، ولكن مع وجود بيانات كافية ، يمكن الحصول على المفتاح دون مشاكل.
مواد مثيرة للاهتمام: