تخيل أنك محاط بجدار عالٍ بلا حدود ، لكن لا يعرف شيئًا عن ما وراء الجدار. الآن تخيل أن تجسيد هذا الجدار هو هذه المعادلة:
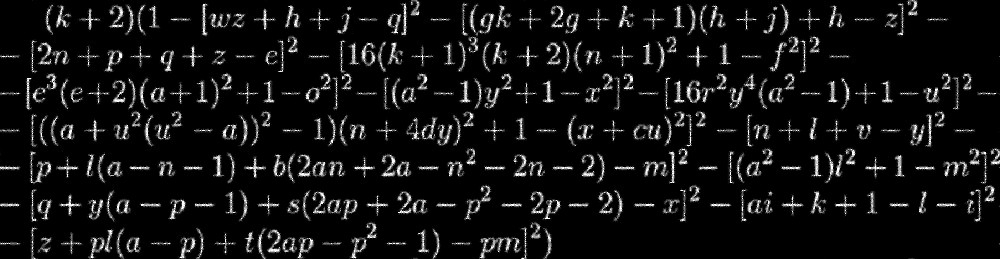
سيكون هذا الاستعارة أسهل في الفهم إذا وضعنا تشابهاً مع وجود ثقب أسود: لا نعرف ما هو في أفق الأحداث ، ومعرفة أننا بحاجة إلى التوصل إلى وسيلة للوصول إلى هناك. يوجد شيء مشابه في عالم الرياضيات. هذه المعادلة هي "صيغة" حقيقية لعدد أولي ، ولكن من أجل استخدامها ، نحتاج إلى معرفة كيفية البحث عن
{a ، b ، c ، d ، e ، f ، g ، h ، i ، j ، k ، l ، m ، n ، o ، p ، q ، w ، v ، x ، y ، z} .
الثقب الأسود وهذه المعادلة هي الحالات النهائية لشيء حقيقي ومجرّد. وإذا كان هناك ما يكفي من التخمينات والأفكار حول الأولى ، ثم حول الثانية ، لا يوجد شيء عملي معروف. ولكن ، ماذا لو كانت حقًا ثقبًا أسودًا "رياضيًا"؟ ألا تشعر بالفضول ماذا يمكن أن يحدث إذا وقعنا تحت الأفق؟
ماذا يتكون الجدار من؟
الأرقام - ليسوا في العالم الحقيقي. هناك سبعة نرد ، وسبعة ذرات ، وسبعة خطايا مميتة ، لكن السبعة نفسها لا وجود لها - إنها تجريدية. نعم ، يمكننا أن نقول أن الأرقام ليست سوى الكثير من الأشياء المجردة ، ومع ذلك ، هذا هو العالم بأسره. عالم فيه ، كما في العالم الحقيقي ، توجد قوانين. فكر هذا الأمر يبدو غريبًا جدًا. ومع ذلك ، فإن وجود مثل هذا الفرع من الرياضيات كما نظرية الأعداد يشير إلى أن هذا "الغريب" مهم للغاية بالنسبة لنا.
الشيء الأكثر إثارة هو أنه من بين هذه الأشياء الخيالية هناك أشياء خاصة - الأعداد الأولية. إنهم مثل الفوضى الحتمية - يمكن التنبؤ بها ولا يمكن التنبؤ بها في نفس الوقت ، وهذا يتوقف على نطاق نظرهم. على سبيل المثال ، نظرًا لوجودهم ، يمكننا أن نلاحظ أن عددهم أمام عدد تعسفي n لن يتجاوز:
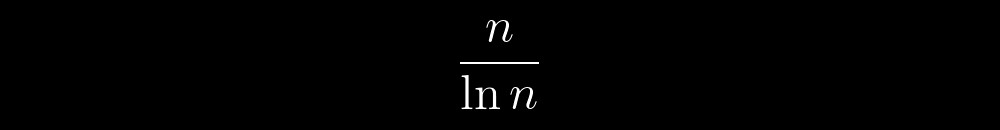
عند تغيير المقياس ، نبدأ في ملاحظة الكثير من التلميحات حول بعض القواعد الداخلية لسلوكهم. تدريجيا ، أصبحت هذه التلميحات كثيرة للغاية. في كثير من الأحيان الأسئلة "من أين أتوا؟" ، "ماذا لو كان هناك خوارزمية معينة للحصول على الأعداد الأولية؟" ، "ماذا لو كان يمكن الحصول على كل عدد أولي باستخدام نفس الخوارزمية؟"
كيف ظهر الجدار
إذا تم الحصول على تسلسل معين من الأرقام كنتيجة لتشغيل خوارزمية معينة ، فإن مجموعة الأرقام من هذا التسلسل تعتبر قابلة للتعداد ، على الرغم من أنها كبيرة للغاية. المجموعات المذكورة لها خاصية واحدة رائعة - ديوفانتاين. هذا يعني أنه يمكن تمثيل أي مجموعة من هذه المعادلات معادلة ديوفانتاين - كثير الحدود مع معاملات عدد صحيح موجب والقوى.
قد يبدو البيان التالي غير قابل للتصديق تمامًا ، ولكن استنادًا إلى هذا التعريف ، يمكننا القول بأن جميع مفاتيح وقيم وظائف التجزئة (حتى bitcoins) يمكن التعبير عنها من خلال معادلات Diophantine. أي المعادلات التي يتم حلها في الأعداد الصحيحة. ونعم ، من الناحية النظرية ، يمكن لأي شخص أن يتعلم أي أسرار ، ويكون شخصًا غنيًا وقويًا بلا حدود. لكن لكي تصبح مثل هذا الشخص ، يجب أولاً استنتاج هذه المعادلات ، ثم حلها.
يمكن للكمبيوتر التعامل مع مهمة تمثيل المجموعة بواسطة معادلة ديوفانتاين ، جزئيًا أو كليًا. ولكن هنا تبرز مشكلة أخرى - معادلات الديوفانتاين لا يتم حلها بشكل عام ، أي لا توجد خوارزمية واحدة لحلها. لا يبدو أن هذا يمثل مشكلة كبيرة ، لأننا نعلم أن بعض المعادلات يتم تمييزها في أشكال منفصلة ، والتي تم إيجاد حل فعال لها بالفعل.
ولكن على الرغم من وجود هذه الأساليب ، فإننا نواجه حتماً صعوبات حسابية مرتبطة إما بدقة الحسابات أو مع سرعة التكرار.
كيف حدث أن الأعداد الأولية كانت تعد؟ تعتمد عملية إنشاء معادلات تمثل مجموعات متعددة على أسس الرياضيات - الحساب والمنطق. وإذا كانت لدينا معرفة كافية بخصائص كائنات مجموعة معينة ، فيمكننا بناءً على هذه المعرفة افتراضات حول الخوارزمية التي تسمح بالحصول عليها. وكما اتضح فيما بعد ، فقد تراكمت معرفة خصائص الأعداد الأولية بما يكفي لهذا الغرض. تم الحصول على المعادلة ، والآن يتم تقليل كل الأسئلة المتعلقة بالأعداد الأولية إليها وحدها.
لكن لا يمكننا حلها.
سمك الجدار والقوة
في الواقع ، نحن نواجه تحديا. ونحن نعرف مقدما عن الهزيمة التي لا مفر منها. ربما يكون التراجع هو القرار الأكثر حكمة. لكن ألا نحتاج إلى هذه الهزائم لكي نتجاوز أنفسنا؟ دعونا نحاول حلها قليلا فقط.
ألقِ نظرة على المعادلة مرة أخرى:
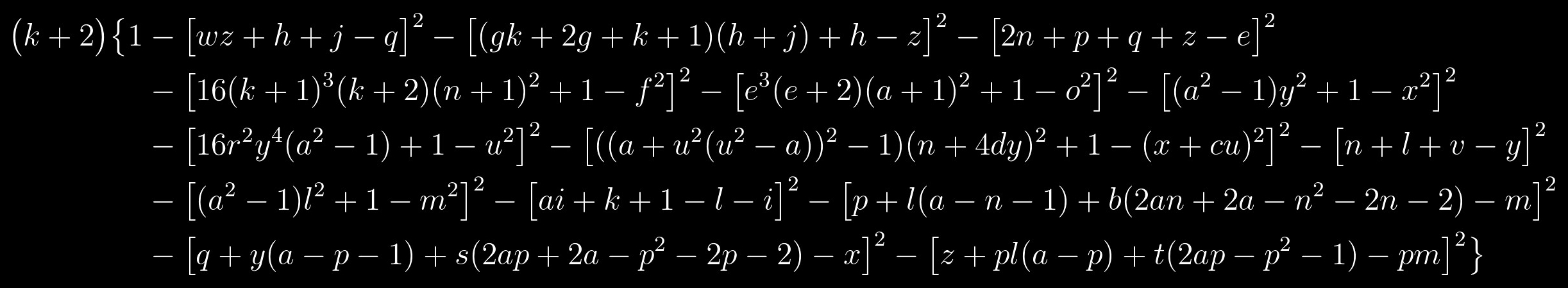
هذا متعدد الحدود تتزامن مجموعته من القيم الإيجابية مع مجموعة الأعداد الأولية. يتكون من عاملين: العامل الأيسر سيكون أولي فقط إذا كان العامل الأيمن ، المشار إليه بين قوسين مجعدين ، يساوي واحدًا ، وهذا ، بدوره ، ممكن فقط إذا كان كل مصطلح في العامل المحدد ، المشار إليه بين قوسين معقوفين ، يساوي الصفر . اتضح أن مسألة حل هذه المعادلة تقلل إلى حل نظام من المعادلات التالية:
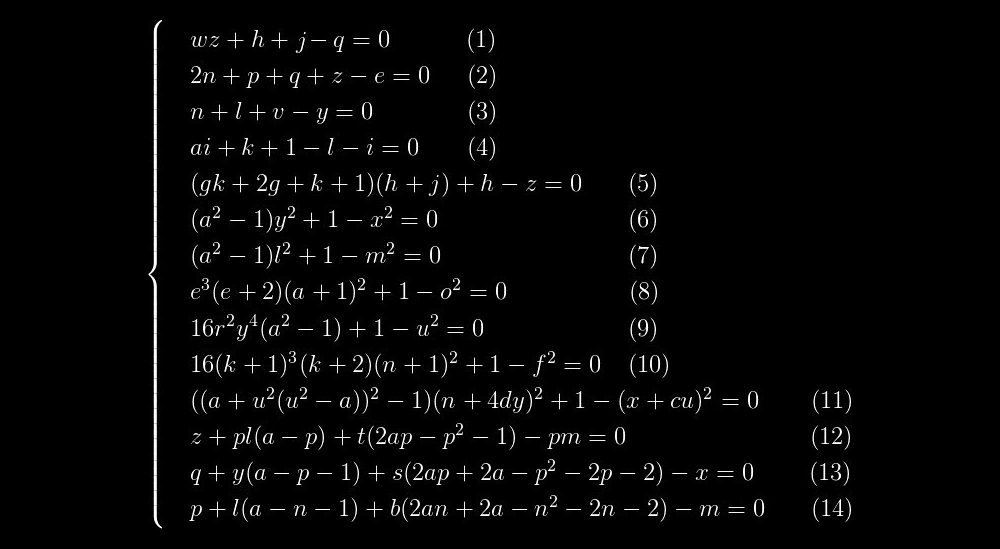
إذا حللنا نظام المعادلات هذا وأضفنا 2 إلى القيمة الموجودة
k ، فسوف نحصل على رقم أولي. ولكن يمكننا أن نذهب في الاتجاه الآخر. خذ عددًا أوليًا ، اطرح 2 منه ، وبالتالي احصل على قيمة
k ، ثم استبدل هذه القيمة في النظام وحاول العثور على قيم المتغيرات المتبقية ذات الصلة بها. بهذه الطريقة سنذهب - حاول إيجاد حل واحد على الأقل لهذه الحدود.
تخضع جميع المتغيرات لقيود صارمة ؛ يجب أن تكون عددًا صحيحًا ولا يمكن أن تكون سالبة. إذا أخذنا
k = 0 ، فإن أول عدد أولي يمكننا الحصول عليه هو 2. ستكون هذه نقطة البداية. بعد استبدال هذه القيمة في نظام المعادلات ، سوف يأخذ الشكل التالي:
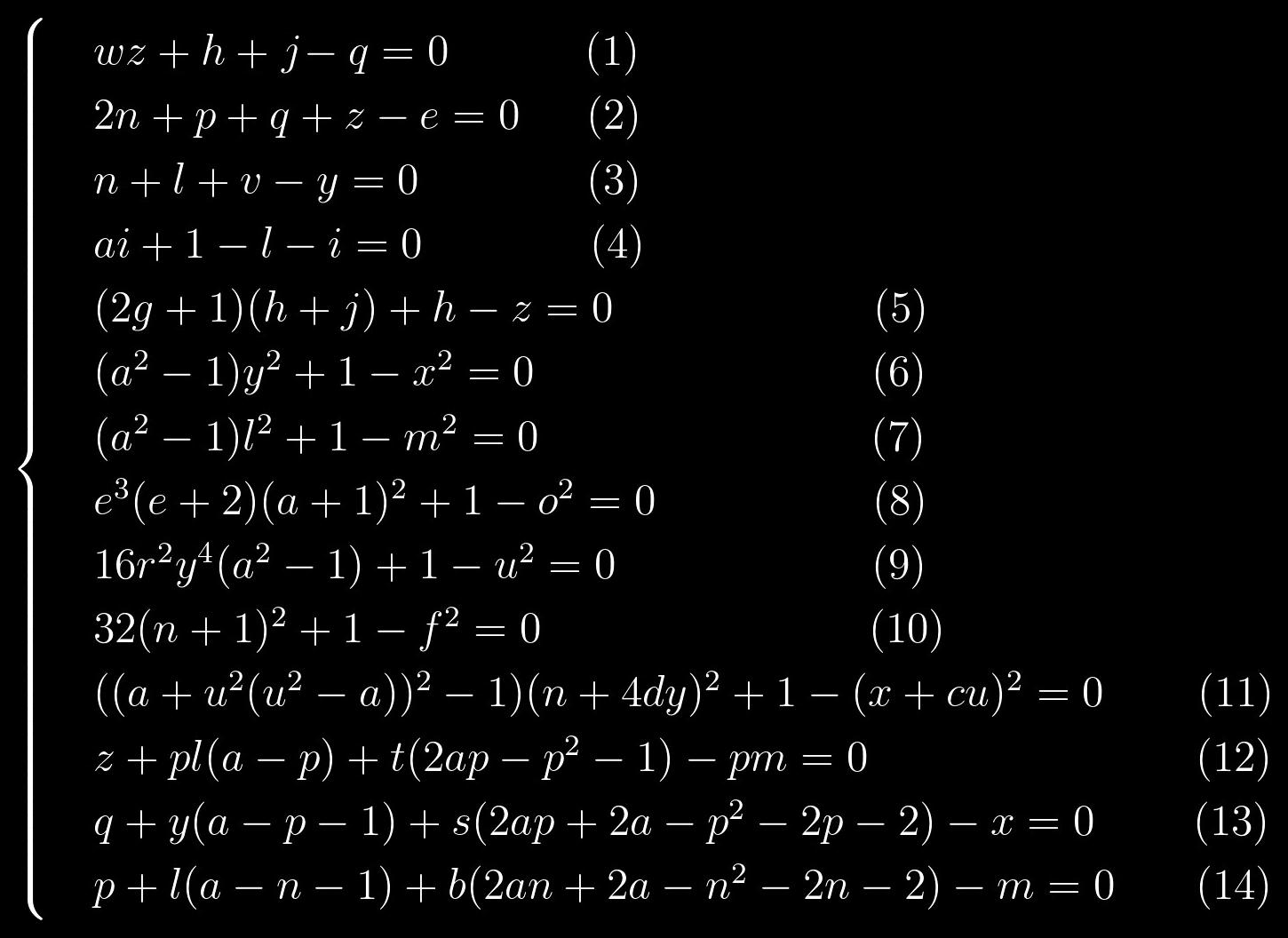
المعادلات (1) - (5) هي معادلات خطية ، أي درجات جميع المتغيرات هي 1. المعادلات (6) - (11) لها بنية متشابهة للغاية. وأخيرًا ، تبرز المعادلتان (12) - (14) أيضًا في مجموعة منفصلة ، وتشبه المعادلتان (13) و (14) بعضهما البعض ، مثل قطرتين من الماء.
يمكننا التخلص من المتغيرات ، أو خفض الدرجة ، لكننا فعلنا ذلك من قبل. يؤدي انخفاض عدد المتغيرات إلى زيادة قوية في درجات المتغيرات الأخرى ، ولا يمكن إجراء انخفاض في درجات المتغيرات إلا من خلال زيادة عددها. لذلك دعونا نحاول حل هذا النظام في هذا النموذج.
المعادلات (6) - (11) هي تعديلات لمعادلة Pell:
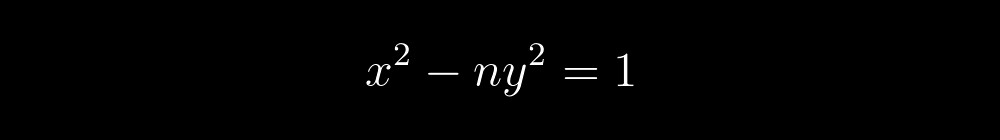
في الواقع ، إذا قمت بإعادة كتابتهم مثل هذا:
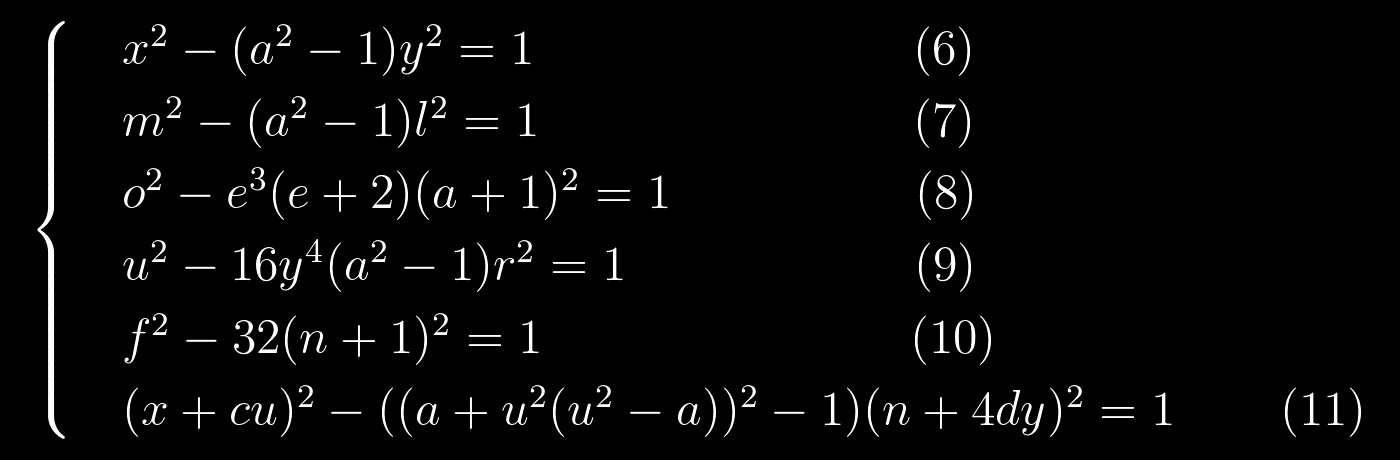
ثم التشابه يصبح واضحا. هذا أمر مشجع للغاية ، لأننا قادرون على حل معادلات بيل بشكل جيد. يمكننا محاولة حل هذا النظام على النحو التالي: أولاً ، نحل معادلة واحدة ، ونستبدل حلولها بمعادلة أخرى ، والتي نحلها أيضًا ، وهكذا دواليك. يبدو الأمر بسيطًا جدًا ، لكنه لن يضر برسم شيء مثل رسم التقليب من أجل معرفة ما يقرب من ذلك على الأقل من أجل حل المعادلات:
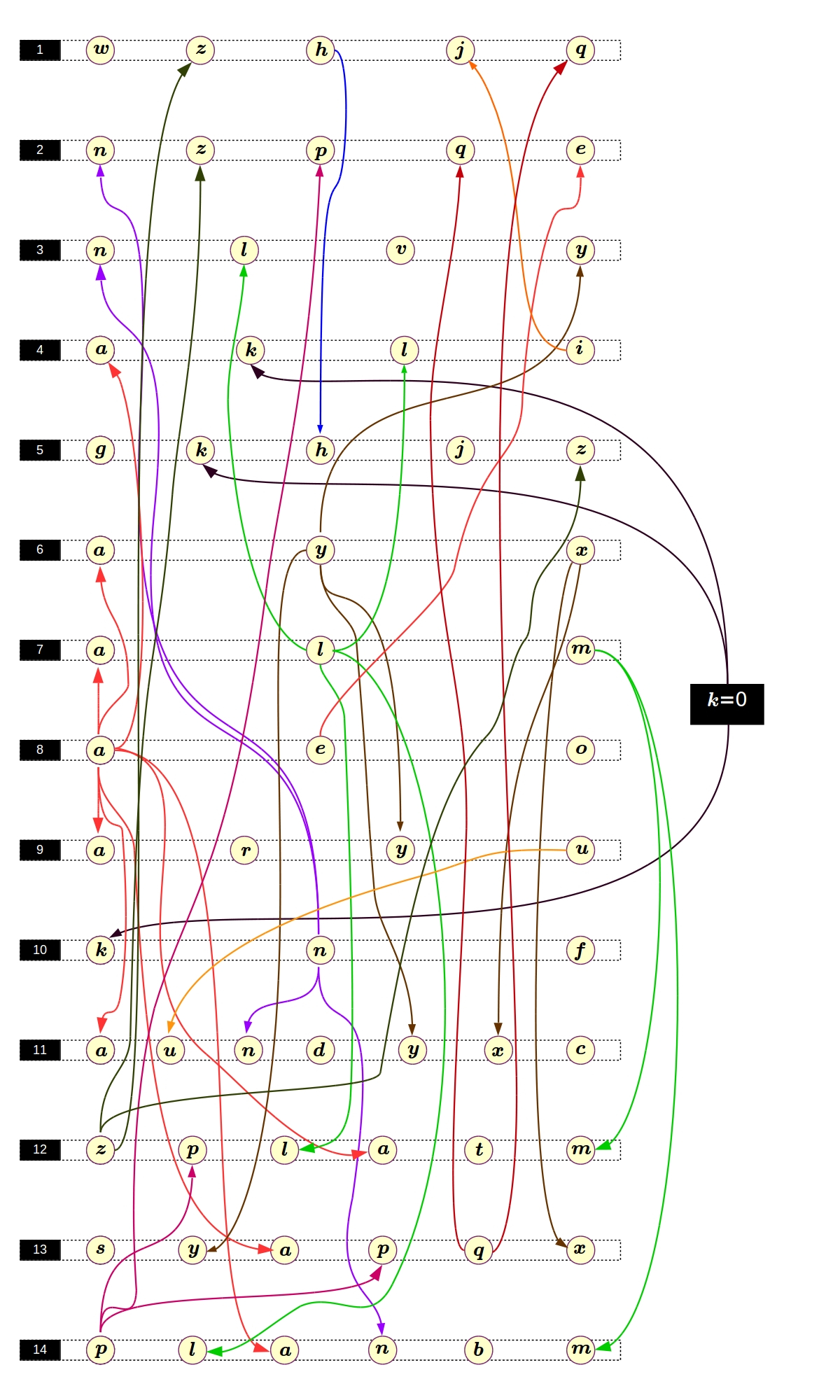
يبدو أن كل شيء بسيط.
ركل على الحائط
نبدأ معادلات بيل. لحلها ، سنقوم بكتابة نص صغير:
from decimal import * getcontext().prec = 50 def peq_dec(N): n = Decimal(N).sqrt() a = int(n) x = n - a p0, q0 = 1, 0 p1, q1 = int(a), 1 while True: a = int(1/x) x = 1/x - a p_i = a*p1 + p0 q_i = a*q1 + q0 if p_i**2 - N*q_i**2 == 1: return p_i, q_i break p0, q0 = p1, q1 p1, q1 = p_i, q_i
بفضله ، يمكننا إيجاد حل للمعادلة (10)
n = 2 ،
f = 17 . ومع ذلك ، قبل الانتقال ، نحتاج إلى معرفة شيء ما عن معادلة Pell.
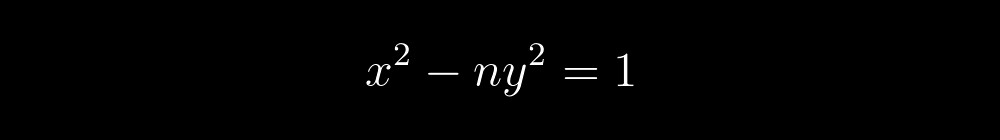
بادئ ذي بدء ، لا يمكن أن يكون مربع كامل. بالإضافة إلى ذلك ، تحتوي أي معادلة Pell على عدد لا حصر له من الحلول ، من بينها دائماً حل بسيط:
x = 1 و
y = 0 . يمكن الحصول على كل قرار لاحق على أساس القرارات السابقة ، وفقًا لمعادلة التكرار التالية:
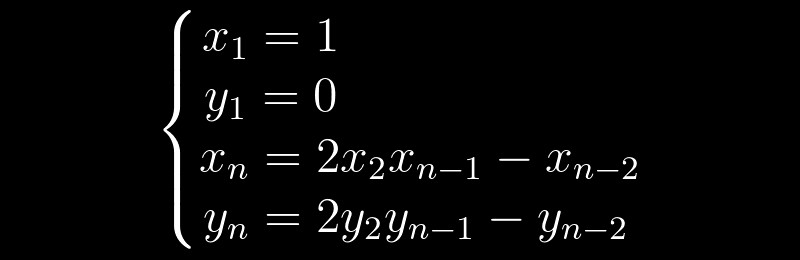
اتضح أنه يكفي بالنسبة لنا أن نجد الحد الأدنى من الحلول غير التافهة ، ويمكننا الحصول على الباقي باستخدام خوارزمية بسيطة. على سبيل المثال ، بالنسبة إلى
n = 2 ، يمكننا بسهولة إيجاد مثل هذا الحل ، فهو
x = 3 و
y = 2 ، ثم تبدو الحلول اللاحقة كما يلي:
17, 12 99, 70 577, 408 3363, 2378 19601, 13860 114243, 80782 665857, 470832 3880899, 2744210 22619537, 15994428 131836323, 93222358 768398401, 543339720 4478554083, 3166815962 26102926097, 18457556052 152139002499, 107578520350 886731088897, 627013566048
هل يستحق مواصلة اتخاذ قرار آخر؟ بالطبع الأمر يستحق ذلك ، لكن ... يمكننا محاولة التنبؤ بما ينتظرنا.
دعنا الآن نتخيل أننا نقوم بحل نظام معادلات من ثلاث معادلات Pell بالشكل التالي:
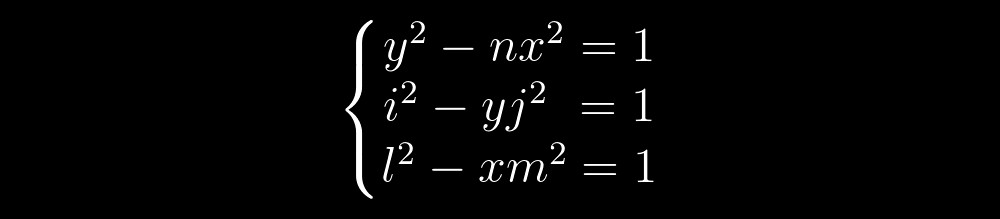
الحل لأي معادلة Pell هو نقاط القطع الزائدة مع الإحداثيات الصحيحة. بعد ذلك ، يمكننا أن نتخيل حلاً للمعادلتين الأوليين مثل هذا:
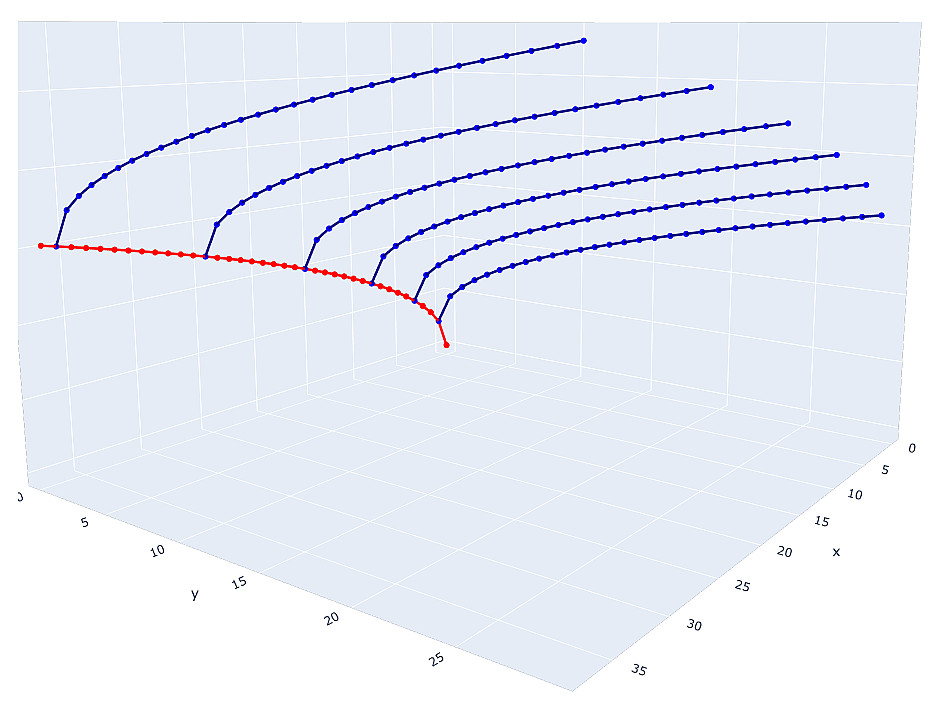
حل المعادلة الأولى هو النقاط الصحيحة للقطع الزائد الأحمر ، لكن إحداثي
y لكل نقطة من هذه النقطة موجود في المعادلة الثانية ويمكن أن يولد أي قطع زرقاء زرقاء تكون نقاطه الصحيحة هي حل المعادلة الثانية.
حتى هذا المخطط التخطيطي يكفي لفهم أننا نتعامل مع عدد كبير جدًا من المرشحين المحتملين لحل النظام. لماذا المرشحين؟ لأن بعض النقاط الصحيحة للقطع الزائد ستكون بالضرورة مربعات كاملة ، على سبيل المثال حلول غير مناسبة. وإذا كنت تتخيل فرض أي شروط إضافية على كل متغير في النظام ، فسيصبح العثور على مرشحين للحل أمرًا بالغ الصعوبة. وحتى الآن نتحدث فقط عن نظام من ثلاث معادلات.
ولكن دعونا نعود إلى "صيغة" الأعداد الأولية لدينا. ماذا يمكن أن يكون أمامنا؟
عاجلاً أم آجلاً ، سنجد أن المعلمة
n في معادلة Pell ستصبح كبيرة كارثية. سوف تصبح طريقة الكسور المستمرة عديمة الفائدة. سنحاول بالتأكيد شيئًا آخر ، على سبيل المثال تعداد القيم مع غربلة ، تعميم العملية بأكملها بطريقة ما والتوصل إلى خوارزميات مثل المنخل التربيعي أو غربال حقل العدد. في النهاية ، سوف نركز على طريقة "شقرافال" ، على الرغم من أنها ستواجه بعض الصعوبات أيضًا.
في لحظة معينة ، سنشعر ببعض الثقة في حل كل معادلة فردية للنظام. ولكن ليس النظام بأكمله. سنحاول تطبيق بعض أساليب التحسين الاسترشادي ، على سبيل المثال ، خوارزمية التلدين ، أو خوارزمية ant. ولكن هنا سوف نفشل. من أجل فهم أسباب هذه الإخفاقات بطريقة أو بأخرى على الأقل ، سيتعين علينا الغوص قليلاً في الهندسة الجبرية والطوبولوجيا. تدريجيا ، سوف نحصل على فكرة عن "المادة القابلة للتبلور". يمكننا أن نتخيل عن بعد بنية السطح الفائق الذي نطلق عليه النمل.
بناءً على هذه الأفكار ، سنحاول تحسين خوارزمياتنا. للقيام بذلك ، سنتخذ أفضل الإنجازات من العديد من فروع الرياضيات. تدريجيا ، ستكون هناك فرصة أقل في الخوارزميات ، لكن لا يزال يتعذر عليك التخلص منها. ماذا سيحدث بعد ذلك؟ وجدنا فجأة أن العديد من المرشحين المناسبين لاتخاذ قرار حقيقي في بعض الأماكن كثيفة المفارقة. كل هذه الكثافة سوف تعطي الأمل في مكان ما في وسطها يتم إخفاء الإجابة الخفية. ستبدو مثل هذه الكثافة للنمل كشيء يشبه فرط الموجات المقلوب. سنحاول "ضرب" مراكزهم وأعلى المستويات. لكن ماذا سيحدث؟
ما وراء الجدار؟
ربما لا أعرف كيف ، لكننا سنحل هذه المعادلة. ربما الكم أو (!) أجهزة الكمبيوتر كوارك سوف تساعدنا. ولكن هذا لن يصبح ثقبًا في الحائط. من المحتمل أن الأعداد الأولية الغوسية ومعادلة أكثر تعقيدًا تمثل الكثير منها سوف تنتظرنا أكثر. بعد ذلك ، ربما ، من بين أرقام hypercomplex الأخرى ، سنواجه مرة أخرى نوعًا من السلوك "البسيط". ربما يكون هذا ، في النهاية ، هو الحد ، وهو نوع من أفق الحدث لثقب أسود رياضي.
ماذا يمكن أن يكون تحت هذا الأفق؟ ربما نوعا من التفرد الرياضي. ربما ، سوف نعرف كل شيء تمامًا عن كل المجموعات ، وسنكون قادرين على حل أي معادلات وأي مشاكل. أو ربما لن يكون هناك أسئلة ومهام جديدة على الإطلاق؟
إنها بالضبط تلك الأفكار التي تنشأ. حسنًا ، في الواقع ، اطرح أي سؤال حول الأعداد الأولية وبفضل هذه المعادلة يمكنك الحصول على إجابة عليها. هو عدد من التوائم الأولية لا حصر له؟ حل هذه المعادلة ، وجعل بضع حسابات جبري والحصول على الجواب. ما هي الأعداد الأولية التي تنتهي في 1 أو 3 أو 7 أو 9؟ نفس الخوارزمية: بضع حسابات واستبدال المعادلة. هل تريد تحلل الأرقام بسرعة إلى عوامل أولية؟ ..
في الختام
قابلت هذه المعادلة لأول مرة في عام 2008 ، حينها كنت مجنونةً بالفعل من نظرية التشفير والأرقام ، ولا سيما مخطط RSA ومشكلة التعمير. بالطبع ، بدا لي أن الأعداد الأولية متعددة الحدود بالنسبة لي موضوع مهم للغاية ، لكنها معقدة للغاية. ومع ذلك ، كانت جميع المشاكل التي يمكن أو لا يمكن حلها مرتبطة بطريقة ما مع معادلات ديوفانتاين. لذلك ، في عام 2014 ، انتقلت مرة أخرى إلى هذا الحد متعدد الحدود ، وقررت ببساطة استكشاف جميع أقسام الرياضيات على التوالي والبحث عن شيء يمكن أن يكون مفيدًا في حلها. بالطبع ، لا يمكن الحديث عن أي ثقافة أكاديمية حول جميع أعمالي - لم أحتفظ أبداً بسجلات منتظمة ، ولم أقم بتجميع الشفرة التي تم إنشاؤها. هذه مجرد هوايتي.
ظهرت فكرة كتابة هذا المقال بعد أن رأيت فيلم Interstellar. لم أستطع أن أصدق أن الثقوب السوداء والجاذبية يمكن أن تكون مثيرة للغاية. ولكن ، كما اتضح فيما بعد ، فإن عالم الرياضيات "غير الموجود" قدم لي نفس الانطباعات طوال الوقت. يحتوي هذا العالم أيضًا على "فضاء عميق" لا يمكن الوصول إليه و "جزيئاته الأولية".
مع هذا المقال أردت أن أوضح أنه من الممكن الاقتراب قليلاً على الأقل من أي مهمة أصعب أو مستحيلة. هناك الكثير من هذه المهام ، ويمكنك اختيار واحدة ترضيك والأقرب إلى مجال الاهتمام. بطبيعة الحال ، فإن التعقيد المفرط والهزيمة المضمونة سيحرمان من أدنى رغبة في هذا المشروع. لكن المفارقة هي أن أكثر الرحلات والمغامرات إثارة للاهتمام ، حتى في عالم الرياضيات "غير الموجود" ، في معظم الأحيان ، تبدأ بهذه الطريقة.