تحتوي القطعة الأكثر شعبية في تاريخ StackOverflow على خطأ!

كشفت دراسة حديثة ، بعنوان "استخدام قصاصات الكود Stack Overflow في مشاريع GitHub وإسنادها" ، فجأة أنه في معظم الأوقات في مشاريع مفتوحة المصدر ، تمت كتابة إجابتي قبل عشر سنوات تقريبًا. ومن المفارقات أن هناك خطأ.

ذات مرة ...

مرة أخرى في عام 2010 ، كنت جالسًا في مكتبي وأمارس الهراء: كنت مولعًا بلعبة الكود وأضفت تصنيفًا إلى Stack Overflow.

جذب السؤال التالي انتباهي: كيفية عرض عدد البايتات بتنسيق قابل للقراءة؟ بمعنى ، كيفية تحويل شيء مثل 123456789 بايت إلى "123.5 ميغابايت".


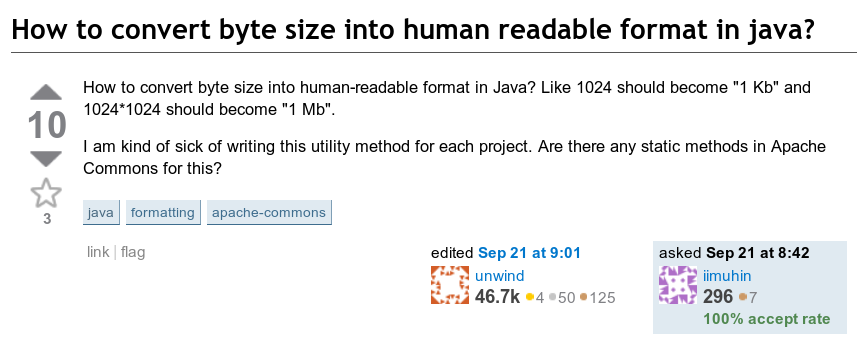واجهة 2010 قديمة جيدة ، بفضل آلة Wayback

ضمنياً ، ستكون النتيجة عددًا يتراوح بين 1 و 999.9 مع الوحدة المناسبة.

كان هناك بالفعل إجابة واحدة مع حلقة. الفكرة بسيطة: تحقق من جميع الدرجات من أكبر وحدة (EB = 10 ¹⁸ بايت) إلى الأصغر (B = 1 بايت) وتطبيق الأول ، وهو أقل من عدد البايتات. في الكود الزائف ، يبدو مثل هذا:

suffixes = [ "EB", "PB", "TB", "GB", "MB", "kB", "B" ] magnitudes = [ 10^18, 10^15, 10^12, 10^9, 10^6, 10^3, 10^0 ] i = 0 while (i < magnitudes.length && magnitudes[i] > byteCount) i++ printf("%.1f %s", byteCount / magnitudes[i], suffixes[i]) 

عادة ، مع الإجابة الصحيحة مع تصنيف إيجابي ، من الصعب اللحاق به. في المصطلح Stack Overflow ، يطلق عليه اسم مشكلة الأسرع في الغرب . لكن هنا كان للإجابة العديد من العيوب ، لذلك ما زلت آمل أن أتجاوزها. على الأقل رمز مع حلقة يمكن تخفيض كبير.

حسنًا ، هذا جبر ، كل شيء بسيط!

ثم اتضح لي. البادئات هي كيلو ، ميجا ، جيجا ، ... - لا شيء أكثر من درجة 1000 (أو 1024 في معيار IEC) ، لذلك يمكن تحديد البادئة الصحيحة باستخدام اللوغاريتم ، وليس الدورة.

بناءً على هذه الفكرة ، قمت بنشر ما يلي:

 public static String humanReadableByteCount(long bytes, boolean si) { int unit = si ? 1000 : 1024; if (bytes < unit) return bytes + " B"; int exp = (int) (Math.log(bytes) / Math.log(unit)); String pre = (si ? "kMGTPE" : "KMGTPE").charAt(exp-1) + (si ? "" : "i"); return String.format("%.1f %sB", bytes / Math.pow(unit, exp), pre); } 

بالطبع ، هذا ليس قابلاً للقراءة ، وسجل / أسرى الحرب أقل كفاءة في الخيارات الأخرى. ولكن لا توجد حلقة ولا يكاد يوجد أي متفرعة ، وبالتالي فإن النتيجة جميلة ، في رأيي.

الرياضيات بسيطة . يتم التعبير عن عدد البايتات كـ byteCount = 1000 ^s ، حيث تمثل s الدرجة (في التدوين الثنائي ، القاعدة هي 1024.) الحل s يعطي s = log ₁₀₀₀ (byteCount).

لا يوجد سجل تعبير بسيط ₁₀₀₀ في API ، ولكن يمكننا التعبير عنه من حيث اللوغاريتم الطبيعي كما يلي s = log (byteCount) / log (1000). بعد ذلك نقوم بتحويل s إلى int ، لذلك إذا كان لدينا ، على سبيل المثال ، أكثر من ميغا بايت واحد (ولكن ليس غيغا بايت كامل) ، فسيتم استخدام MB كوحدة قياس.

اتضح أنه إذا كانت s = 1 ، فإن البعد هو كيلو بايت ، وإذا كانت s = 2 - ميغابايت وهكذا. قسّم البايت كاونت على 1000 ^ثانية واضبط الحرف المقابل في البادئة.

كل ما تبقى هو الانتظار ورؤية كيف ينظر المجتمع إلى الإجابة. لم أستطع أن أعتقد أن هذه الشفرة ستصبح الأكثر انتشارًا في تاريخ Stack Overflow.

دراسة الإسناد

سريع إلى الأمام حتى عام 2018. ينشر طالب الدراسات العليا سيباستيان باليتس مقالًا في المجلة العلمية " هندسة البرمجيات التجريبية " بعنوان "استخدام قصاصات كود المكدس وإضافتها في مشاريع جيثب" . موضوع بحثه هو مدى احترام ترخيص Stack Overflow CC BY-SA 3.0 ، أي هل يشير المؤلفون إلى Stack Overflow كمصدر للتعليمات البرمجية؟

للتحليل ، تم استخراج مقتطفات من الشفرة من تفريغ Stack Overflow وتم تعيينها إلى الكود في مستودعات GitHub العامة. اقتباس من الملخص:

نقدم نتائج دراسة تجريبية واسعة النطاق لتحليل استخدام وإسناد شظايا غير تافهة من كود جافا من إجابات SO في مشاريع GitHub العامة (GH).

(Spoiler: لا ، معظم المبرمجين لا يمتثلون لمتطلبات الترخيص).

المقالة لديها مثل هذا الجدول:



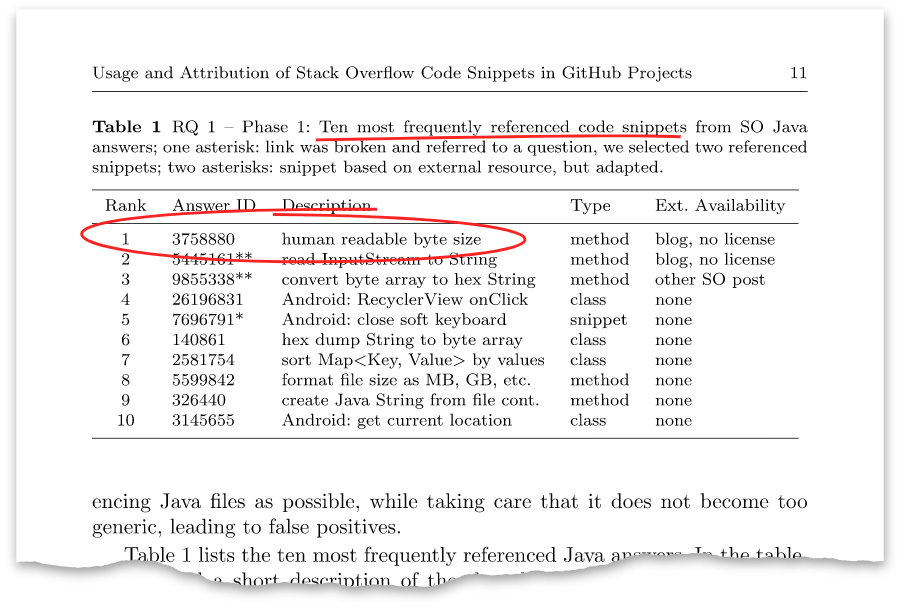
تبين أن الإجابة المذكورة أعلاه ذات المعرف 3758880 هي الإجابة التي نشرتها قبل ثماني سنوات. في الوقت الحالي ، لديه أكثر من مائة ألف مشاهدة وأكثر من ألف إيجابيات.

يؤدي البحث السريع على GitHub إلى إنتاج الآلاف من المستودعات باستخدام الرمز humanReadableByteCount .



ابحث عن هذه القطعة في مستودعك:

 $ git grep humanReadableByteCount 

قصة مضحكة ، كما علمت عن هذه الدراسة.

عثر Sebastian على تطابق في مستودع OpenJDK دون أي إسناد ، ورخصة OpenJDK غير متوافقة مع CC BY-SA 3.0. في قائمة المراسلات jdk9-dev ، سأل: هل تم نسخ كود Stack Overflow من OpenJDK أو العكس؟

الشيء المضحك هو أنني عملت للتو في Oracle ، في مشروع OpenJDK ، لذلك كتب زميلي وصديقي السابق ما يلي:

مرحبا،

لماذا لا تسأل مؤلف هذا المنشور مباشرة على SO (aioobe)؟ وهو عضو في OpenJDK وعمل في Oracle عندما ظهر هذا الرمز في مستودعات مصدر OpenJDK.

أوراكل يأخذ هذه القضايا على محمل الجد. أعلم أن بعض المديرين شعروا بالارتياح عندما قرأوا هذه الإجابة وعثروا على "الجاني".

ثم كتب لي سيباستيان لتوضيح الموقف ، وهو ما قمت به: تمت إضافة هذا الرمز قبل انضمامي إلى Oracle وليس لدي أي علاقة بالالتزام. من الأفضل عدم المزاح مع Oracle. بعد أيام قليلة من فتح التذكرة ، تم حذف هذا الرمز.

بق

أراهن أنك فكرت بالفعل في ذلك. أي نوع من الخطأ في الرمز؟

مرة أخرى:

 public static String humanReadableByteCount(long bytes, boolean si) { int unit = si ? 1000 : 1024; if (bytes < unit) return bytes + " B"; int exp = (int) (Math.log(bytes) / Math.log(unit)); String pre = (si ? "kMGTPE" : "KMGTPE").charAt(exp-1) + (si ? "" : "i"); return String.format("%.1f %sB", bytes / Math.pow(unit, exp), pre); } 

ما هي الخيارات؟

بعد exabytes (10 ¹⁸ ) هي zettabytes (10 ²¹ ). ربما سوف يتجاوز عدد كبير حقا kMGTPE؟ لا. القيمة القصوى هي 2 ⁶³ -1 ≈ 9.2 × 10 ¹⁸ ، لذلك لن تتجاوز أي قيمة إكسبايت.

ربما الخلط بين وحدات SI والنظام الثنائي؟ لا. كان هناك ارتباك في الإصدار الأول من الإجابة ، ولكن تم إصلاحه بسرعة كبيرة.

ربما ينتهي الأمر بالتصفير ، مما يؤدي إلى تعطل charAt (exp-1)؟ لا كذلك. الأول إذا كان البيان يغطي هذه القضية. ستكون قيمة exp دائمًا 1 على الأقل.

ربما بعض خطأ التقريب غريب في التسليم؟ حسنًا ، أخيرًا ...

العديد من تسعة

يعمل الحل حتى يقترب من 1 ميغابايت. عند تحديد "1000,0 kB" بايت كإدخال ، تكون النتيجة (في وضع SI) هي "1000,0 kB" . على الرغم من أن 999،999 أقرب إلى 1000 × 1000 ¹ من 999.9 × 1000 ¹ ، إلا أن علامة 1000 محظورة بموجب المواصفات. النتيجة الصحيحة هي "1.0 MB" .

في دفاعي ، يمكنني القول أنه في وقت كتابة هذا التقرير ، كان هذا الخطأ في جميع الإجابات المنشورة الـ 22 ، بما في ذلك مكتبات Apache Commons ومكتبات Android.

كيفية اصلاحها؟ بادئ ذي بدء ، نلاحظ أن الأس (exp) يجب أن يتغير من 'k' إلى 'M' بمجرد أن يكون عدد البايتات أقرب إلى 1 × 1000 ² (1 MB) من 999.9 × 1000 ¹ (999.9 كيلو بايت) ). يحدث هذا عند 999،950. وبالمثل ، يجب أن ننتقل من "M" إلى "G" عندما نذهب إلى 999،950،000 وما إلى ذلك.

نحسب هذه العتبة exp إذا كانت bytes أكبر:

 if (bytes >= Math.pow(unit, exp) * (unit - 0.05)) exp++; 

مع هذا التغيير ، يعمل الرمز بشكل جيد حتى يقترب عدد البايتات من 1 EB.

المزيد من تسعة

عند حساب 999 949 999 999 999 999 ، يعطي الكود 1000.0 PB ، والنتيجة الصحيحة هي 999.9 PB . رياضيا ، الكود دقيق ، فماذا يحدث هنا؟

الآن نواجه قيودًا double .

مقدمة لحساب النقطة العائمة

وفقًا لمواصفات IEEE 754 ، فإن قيم النقطة العائمة القريبة من الصفر لها تمثيل كثيف للغاية ، في حين أن القيم الكبيرة لها تمثيل ضئيل للغاية. في الواقع ، يتراوح نصف القيم بين -1 و 1 ، وعندما يتعلق الأمر بالأرقام الكبيرة ، فإن قيمة الحجم Long.MAX_VALUE لا تعني شيئًا. بالمعنى الحرفي.

 double l1 = Double.MAX_VALUE; double l2 = l1 - Long.MAX_VALUE; System.err.println(l1 == l2); // prints true 

انظر "بتات النقطة العائمة" للحصول على التفاصيل.

تتمثل المشكلة في حسابين:

• الانقسام في String.format و
  
• توسيع عتبة exp

يمكننا التبديل إلى BigDecimal ، لكنه ممل. بالإضافة إلى ذلك ، تنشأ المشاكل أيضًا هنا ، لأن واجهة برمجة التطبيقات القياسية لا تحتوي على لوغاريتم BigDecimal .

تقليل القيم الوسيطة

لحل المشكلة الأولى ، يمكننا تقليل قيمة bytes إلى النطاق المطلوب ، حيث الدقة أفضل ، وضبط exp وفقًا لذلك. في أي حال ، يتم تقريب النتيجة النهائية ، لذلك لا يهم أن نتخلص من الأرقام الأقل أهمية.

 if (exp > 4) { bytes /= unit; exp--; } 

إعداد بت الأقل أهمية

لحل المشكلة الثانية ، تكون البتات الأقل أهمية بالنسبة لنا (99994999 ... 9 و 99995000 ... 0 يجب أن يكون لها درجات مختلفة) ، لذلك يتعين علينا إيجاد حل مختلف.

أولاً ، لاحظ أن هناك 12 قيمة عتبة مختلفة (6 لكل وضع) ، وأحدها يؤدي إلى حدوث خطأ. يمكن تحديد نتيجة غير صحيحة بشكل فريد لأنها تنتهي في D00 ₁₆ . حتى تتمكن من اصلاحها مباشرة.

 long th = (long) (Math.pow(unit, exp) * (unit - 0.05)); if (exp < 6 && bytes >= th - ((th & 0xFFF) == 0xD00 ? 52 : 0)) exp++; 

نظرًا لأننا نعتمد على أنماط بتات معينة في نتائج الفاصلة العائمة ، فإننا نستخدم معدّل rigfp لضمان عمل الشفرة بشكل مستقل عن الجهاز.

قيم المدخلات السلبية

ليس من الواضح تحت أي ظرف من الظروف قد يكون لعدد سلبي من وحدات البايت معنى ، ولكن بما أن Java ليس لديها long غير موقعة ، فمن الأفضل معالجة هذا الخيار. الآن ، ينتج إدخال مثل -10000 B

دعنا نكتب absBytes :

 long absBytes = bytes == Long.MIN_VALUE ? Long.MAX_VALUE : Math.abs(bytes); 

التعبير مطول جدًا لأن -Long.MIN_VALUE == Long.MIN_VALUE . نحن الآن نقوم بجميع العمليات الحسابية باستخدام absBytes بدلاً من bytes .

النسخة النهائية

فيما يلي النسخة النهائية من الكود ، مختصرة ومكثفة بروح النسخة الأصلية:

 // From: https://programming.guide/the-worlds-most-copied-so-snippet.html public static strictfp String humanReadableByteCount(long bytes, boolean si) { int unit = si ? 1000 : 1024; long absBytes = bytes == Long.MIN_VALUE ? Long.MAX_VALUE : Math.abs(bytes); if (absBytes < unit) return bytes + " B"; int exp = (int) (Math.log(absBytes) / Math.log(unit)); long th = (long) (Math.pow(unit, exp) * (unit - 0.05)); if (exp < 6 && absBytes >= th - ((th & 0xfff) == 0xd00 ? 52 : 0)) exp++; String pre = (si ? "kMGTPE" : "KMGTPE").charAt(exp - 1) + (si ? "" : "i"); if (exp > 4) { bytes /= unit; exp -= 1; } return String.format("%.1f %sB", bytes / Math.pow(unit, exp), pre); } 

لاحظ أن هذا بدأ كمحاولة لتجنب الحلقات المتفرعة. ولكن بعد تخفيف جميع المواقف الحدودية ، أصبح الرمز أقل قابلية للقراءة من الإصدار الأصلي. شخصيا ، أنا لن نسخ هذه الشظية في الإنتاج.

للحصول على إصدار محدث من جودة الإنتاج ، راجع مقالة منفصلة: "تنسيق حجم البايت بتنسيق قابل للقراءة . "

النتائج الرئيسية

• قد تكون هناك أخطاء في الإجابات على Stack Overflow ، حتى إذا كانت تحتوي على آلاف المزايا الإضافية.
  
• تحقق من كل الحالات الحدودية ، خاصةً في الكود باستخدام Stack Overflow.
  
• حساب النقطة العائمة معقد.
  
• تأكد من تضمين الإسناد الصحيح عند نسخ الكود. قد يأخذك شخص لتنظيف المياه.