طريقة Y هي طريقة سهلة حقا لبناء مكعب روبيك

مقدمة

يناقش المقال "طريقة Y" لتجميع مكعب روبيك - من السهل أن نفهمه ونتذكره. يعتمد على تسلسل واحد فقط ، والذي يسمى "Y- الحركة". بعد فهم هذه الخوارزمية ، من غير المرجح أن تنسى كيفية تجميع المكعب بنفسك.

إذا حاولت استخدام google لتعليمات التجميع لـ Rubik's Cube ، فهناك العديد من الخيارات مع وصف "التجميع البسيط" ، بما في ذلك على Wikipedia . التي ، بشكل عام ، هي حقا بسيطة جدا لفهم ، ولكن لديها عيب كبير. من أجل تجميع مكعب ، تحتاج إلى معرفة خمسة أو أكثر من التسلسلات غير التافهة (الخوارزميات) لإعادة ترتيب مكعبات فردية ، لتجميع مكعب روبيك في طبقات. في هذا الصدد ، من الصعب تذكر هذه التعليمات وإعادة إنتاجها بشكل مستقل. في الآونة الأخيرة ، تعثرت بطريق الخطأ عند ذكر الخوارزمية " الحل النهائي لمكعب روبيك " ، الذي زُعم أنه سهل التذكر والفهم ، ويستخدم متسلسلين فقط. وعندما بدأت في معرفة المزيد من التفاصيل ، وجدت أيضًا خوارزمية أخرى - " الطريقة Y " ، وهي أيضًا بسيطة وتستخدم تسلسلًا واحدًا فقط.

لسوء الحظ ، لم أجد وصفًا لهذه الخوارزمية باللغة الروسية ، لذلك قررت ملء هذه الفجوة. يبدو لي أيضًا أن الشيء الرئيسي في هذه الطريقة هو فهم كيفية عملها. لذلك ، هنا لا أقدم مجموعات جاهزة من الحركات لحالات معينة ، لكنني حاولت بدلاً من ذلك أن أصف بمزيد من التفصيل ما يحدث.

تم إنشاء الصور في هذه المقالة باستخدام الأداة على ruwix.com . الروابط على الصور ستفتح هذه الأداة مع المعلمات المقابلة للصورة. هذه إما الحالة الموضحة للمكعب ويمكنك تدويرها بالماوس ، أو في بعض الحالات ، يتم تحديد الحركات الموصوفة هناك ، والتي يمكن "ضياعها" جيئة وذهابا.

حركة Y

أساس هذه الخوارزمية هو الحركة ص. ومكون مهم إلى حد ما من الخوارزمية هو فهم ميكانيكا هذه الحركة.

يُسمى هذا التسلسل من الأدوار لأن المكعبات التي يلمسها تشبه الحرف "Y" ، الذي يتكون من ثلاثة حواف تخرج من زاوية واحدة من المكعب.

حركة Y بسيطة للغاية وتتكون من أربع لفات من وجهين متجاورين ، على سبيل المثال ، اليمين والأمام. في تدوين تناوب شائع لمكعب روبيك ، يبدو كالتالي: R 'FR F'. ما يمكن وصفه على النحو التالي:

1. الجانب الأيمن عكس اتجاه عقارب الساعة بدوره ربع
2. الوجه الأمامي في اتجاه عقارب الساعة ربع بدوره
3. الجانب الأيمن ربع بدوره في اتجاه عقارب الساعة
4. الوجه الأمامي ربع بدوره عكس اتجاه عقارب الساعة

أي أن الوجوه تدور أولاً "تجاه أنفسهم" ، ثم بترتيب عكسي "عن أنفسهم".

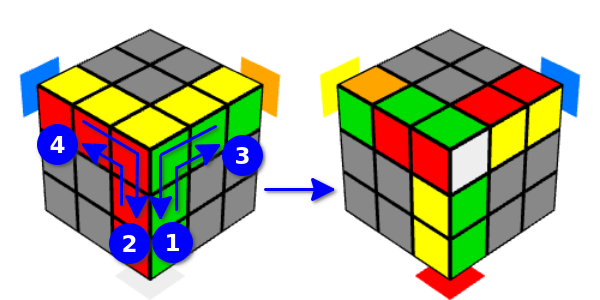
سوف نسمي هذا الخيار "حركة Y الصحيحة" (حيث يتم تدوير الوجه لأول مرة إلى اليمين). في هذه الحالة ، يتغير وضع المكعبات على الحافة ، وهو أمر شائع لهذه الوجوه وعلى الحواف العلوية. إذا بدأت المنعطفات من الوجه الأمامي ، فسوف تتأثر نفس المكعبات ، وسوف نسمي هذا الخيار "Y - حركة اليسار" (حيث يتم تشغيل الوجه أولاً من اليسار).


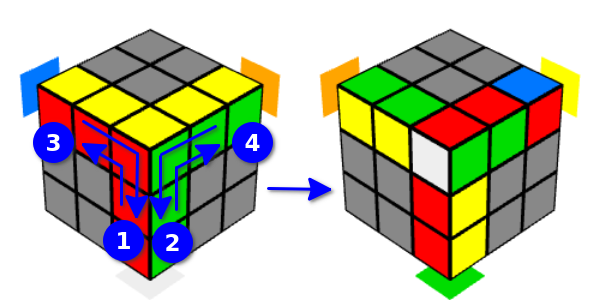
يمكنك أيضًا بدء المنعطفات "بمفردك" - ستكون هي نفسها إذا قلبنا المكعب وبدأنا بمناوبات "على أنفسنا" ، لذلك سنطلق على مثل هذه الخيارات "حركة Y مقلوبة إلى اليمين واليسار". مع حركات Y المقلوبة ، ستتأثر الحافة المجاورة أيضًا ، وليس الحافة العلوية ، ولكن الحواف السفلية المجاورة لها.



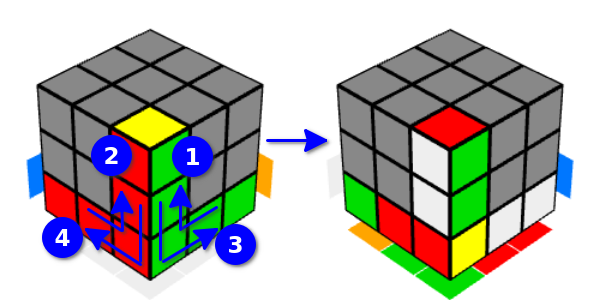
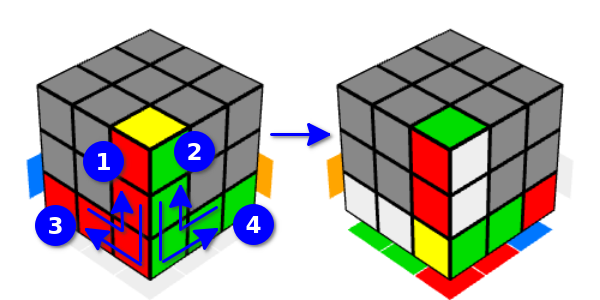
بالطبع ، لا يوجد فرق أساسي في كل هذه الحركات. هذا التنوع هو للراحة فقط.

نحن ندرج بعض خصائص Y-motion:

• حركات Y اليمنى واليسرى معكوسة لبعضها البعض ، أي تسلسل الحركات اليمنى واليسرى واليسرى واليمنى لن يغير حالة المكعب.
• تتسبب إحدى الحركات Y في مكعبين زاوية على وجه مجاور ومكعبات زاوية أخرى لتغيير أماكن الزوج. وتتحرك ثلاثة مكعبات في منتصف الحواف (حواف) في دائرة.
• كما قد تخمن ، بعد حركات ، تعود مكعبات الزاوية إلى أماكنها. ولكن في نفس الوقت يتم تشغيلها.
  
  
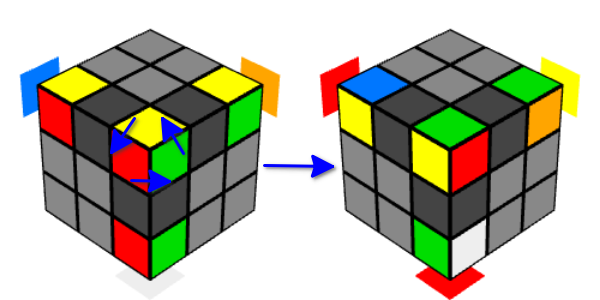
• وإذا قمت بأداء ثلاث مرات في حركتين ، فستدور المكعبات ثلاث مرات ، وبالتالي ستعود إلى حالتها الأصلية.
• تعود مكعبات الحافة إلى حالتها الأصلية بعد دورة من ثلاث حركات.
  
  
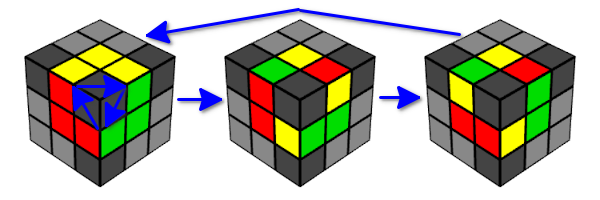
• وبالتالي ، إذا قمت بحركة Y ست مرات متتالية ، فستعود حالة المكعب إلى حالته الأصلية.
• بعد حركة Y واحدة ، تتحرك مكعبات الحافة في اتجاه الدوران الأول ، في حين يبدو أن مكعبين يدوران على طول الوجوه المقابلة (حول محورهما) ، بينما يدور الثالث ، لكنه ينقلب. المكعب الذي يتحرك بين الحواف العليا ، في حالة حركة Y المعتادة (غير المقلوبة) ، ينقلب. عند العمل مع مكعبات الحافة ، يمكن القيام بحركة Y على طول الحواف نفسها من خلال تحويل المكعب في اتجاهات مختلفة ، وبالتالي تحقيق ثورة المكعب التي نحتاج إليها.

تسلسل تجميع المكعب

أولاً ، يتم تجميع الطبقتين السفليتين للمكعب ، باستثناء حافة رأسية واحدة تمر عبر هذه الطبقات. نحن نحتفظ بهذا المكان كمساحة للمناورة. يتم تجميع مكعبات الزاوية السفلية والدنيا ببساطة شديدة ، ولكن إذا كانت هناك صعوبات ، فليس من الصعب للغاية تكييف حركة Y لهذا أو مشاهدة أحد الإرشادات لتجميع الطبقات البسيط للمكعب.


بعد ذلك ، تحتاج إلى جمع المكعبات الوسطى على الحواف الرأسية (الحواف). للقيام بذلك ، قم بتدوير الوجه العلوي باستخدام المكعب المرغوب بحيث يكون على أحد الوجوه المجاورة للحافة المستهدفة. وأيضًا مؤقتًا (لا تنسَ بعد ذلك العودة إلى المكان) لتدوير الوجه السفلي بحيث يوجد في مكانه الحافة المستهدفة مكعب ، تركناه بدون تجميع. يمكنك الآن استخدام حركة Y لنقل المكعب من الوجه العلوي إلى المكان الذي نحتاج إليه. يجب القيام بحركة Y بحيث يدور مكعب الحافة هذا في الاتجاه الصحيح نحو الضلع ، وعندئذٍ ينقلب.

إذا لم يكن المكعب المرغوب على الوجه العلوي ، فمن الضروري "تحريره" من هناك مسبقًا ، وأيضًا بحركة Y ، دون أن ننسى مرة أخرى بديلاً للزاوية غير المفككة على الوجه السفلي.


حتى الآن ، قمنا بجمع الطبقتين السفليتين بدون حافة واحدة. بعد ذلك ، سوف نحتاج إلى جمع مكعبين من الحواف على الحواف العلوية ، لا يتطابقان مع ما لا نجمعه على وجه التحديد. بعد ذلك ، من مكعبات الحافة ، سيبقى ثلاثة مفكك فقط ، على الحواف التي تشكل الحرف "Y": الحافة الرأسية التي لم نجمعها ، والحافتان العلويتان المتجاورتان لها.


وبالطبع ، نجمعها باستخدام حركة Y أو أكثر ، ونقلبها ونضعها في الأماكن الصحيحة. هنا تحتاج فقط إلى أن تأخذ في الاعتبار لحظة واحدة مع عدد التباديل ، والتي يرد وصفها أدناه قليلا.
عند تجميع مكعبات الحافة الخمسة الأخيرة ، قد نحتاج إلى إلغاء تحريك هذه الحرف "Y" لجعل الحركة Y في الاتجاه الآخر (تحويل الوجوه الأخرى على طول هذه الحواف) ، وبالتالي تحقيق حركة المكعبات التي نحتاجها إلى أماكن أخرى مع أو بدون ثورة.



في هذه المرحلة ، سيكون لدينا مكعب تجميعيًا تقريبًا لا يتم فيه تجميع مكعبات الزاوية الموجودة على الوجه العلوي وعلى الحافة الرأسية التي لم نجمعها. باستخدام الطرق الموضحة أدناه ، نقوم أولاً بإعادة ترتيب الزوايا مع بعضها البعض بحيث تكون في أماكنها ، وربما تكون موجهة بشكل غير صحيح. ثم نشرناهم.

الصيحة ، يتم تجميع مكعب لدينا!

نحن نعتبر التباديل

ما تحتاج إلى الانتباه إليه عندما نقوم بجمع مكعبات الحافة الخمسة الأخيرة. عندما يتبقى ثلاثة منهم فقط ، من أجل أن ينجح كل شيء في إعادة ترتيبهم في الحرف "Y" ، من الضروري أن يكونوا جميعًا في أماكنهم (ربما رأسًا على عقب) أو يجب أن يكونوا جميعًا في غير محله. هذا يرجع إلى حقيقة أن حركة Y تعيد ترتيب ثلاثة مكعبات حافة في وقت واحد. إذا أخذنا في الاعتبار ذلك من وجهة نظر التبادلات الزوجية للمكعبات في الأماكن على الحواف المجاورة ، فهناك تبادلتان (التباديل). الآن يجب أن يكون من الواضح لماذا ، في حالة وجود مكعبين بالضبط من مكانه ، فلن نكون قادرين على جمعهما. لأن نحن بحاجة إلى عمل تقليب واحد ، وبمساعدة حركات Y ، يمكننا فقط القيام بعدد من التباديل.

ماذا تفعل في هذه الحالة؟ لاحظ أنه إذا قمت بتدوير وجه المكعب ، فإننا نتبادل أربعة مكعبات حواف في نفس الوقت ، أي ما يعادل ثلاثة التباديل ، أي عدد فردي ، وهو ما نحتاجه. من هذا ، يجب أن يكون الوجه العلوي موجهًا بشكل صحيح حتى نتمكن من جمع مكعبات الحافة الثلاثة الأخيرة. إذا حدث ذلك أن مكعبات الحافة الثلاثة الأخيرة تتطلب تقليبًا واحدًا ، فهذا يعني أنك بحاجة إلى إعادة ترتيب مكعبات الحافة المجمعتين بالفعل على الوجه العلوي في الأماكن المجاورة.

بالإضافة إلى ذلك ، يمكننا حساب مسبقًا ، قبل تجميع أول مكعبين من هذه الخمسة ، عدد التباديل التي ستكون مطلوبة لوضع جميع مكعبات الحافة الخمسة في مكانها. إذا كان هذا الرقم متساويًا ، فسيتم توجيه الحد العلوي بشكل صحيح. وإذا كان الأمر غريبًا ، فأنت بحاجة إلى تحويله مرة واحدة في أي اتجاه. وبالتالي ، يمكننا وضع هذين الزهر على الفور في الأماكن الصحيحة.

العمل مع مكعبات الزاوية

في المرحلة الأخيرة من التجميع ، نحتاج إلى إعادة ترتيب مكعبات الزاوية في الأماكن وتدويرها. للقيام بذلك ، نستخدم الخصائص المذكورة سابقًا لحركة Y فيما يتعلق بمكعبات الزاوية. لأن إنه أكثر ملاءمة للعمل مع مكعبات الزاوية الموجودة على الوجه العلوي ، ولهذا سنستخدم حركة Y المقلوبة (تبدأ بدورها "بعيدًا عنك"). في هذا القسم ، سيتم استخدام هذه الخيارات دون مزيد من التوضيح. دعونا نلاحظ على الفور أن هذه الحركة تغير حالة مكعب واحد فقط على الوجه العلوي - وهذا مكعب زاوي على "الحافة المجاورة".

لإعادة ترتيب مكعبات الزاوية ، نلاحظ أن حركة Y واحدة (على اليمين واليسار) تقوم بتبادل زوج من مكعبات الزاوية على "الحافة المجاورة" ، وأن الاستخدام المتسلسل للحركة Y اليمنى واليسرى (أو اليمين واليسار) يُرجع المكعب بالكامل في الحالة الأولية. دعونا نفكر فيما يحدث إذا قمنا بتدوير الوجه العلوي بين هذه الحركات. كما لاحظنا بالفعل ، في الجانب العلوي ، يتغير مكعب واحد فقط في الزاوية ، ويتم إعادة ترتيبه باستخدام مكعب زوج على الحافة. في هذه الحالة ، سيكون لدينا تبادلتان لمكعبات الزاوية على الحافة ، ولكن في كل مرة سيتم استبدال زاوية مختلفة في الأعلى ، وستظل جميع المكعبات الأخرى كما هي (بالطبع ، لا يزال عليك تذكر تدوير الوجه العلوي إلى حالته الأصلية). وبالتالي ، تبادلنا أماكن مكعبات الزاوية الثلاثة - واحدة من الأسفل واثنتان من الأعلى.


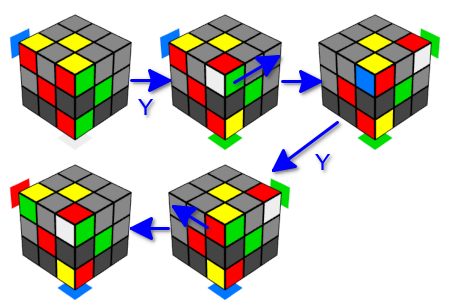
الآن سنتعامل مع دوران المكعبات. للقيام بذلك ، استخدم خدعة مماثلة. سنفعل حركات Y متتالية في اتجاه واحد. نتيجة لذلك ، تبقى مكعبات الزاوية في مكانها ، لكن مع تغيير اتجاهها. نحن هنا مهتمون بخيارين لمجموعة من الحركات: ثلاث حركات مزدوجة في اتجاه واحد (يسار أو يمين) أو حركة مزدوجة في اتجاه واحد وحركة مزدوجة في الاتجاه المعاكس. في كل من هذه الخيارات ، يعود المكعب بالكامل إلى حالته الأصلية. ومرة أخرى ، سنستبدل بين الحركات المزدوجة الزاوية التالية التي نحتاجها بدلاً من الزاوية العليا من "الضلع المجاور". وبالتالي ، يمكننا تدوير ثلاثة مكعبات زاوية على وجه واحد في اتجاه واحد ، أو مكعبين زاوية على وجه واحد في اتجاهات مختلفة ، دون تغيير حالة مكعبات المتبقية. لاحظ أنه بعد حركة مزدوجة ، يدور المكعب العلوي من الضلع المجاور في نفس الاتجاه الذي يتم فيه تنفيذ أول حركة ص.

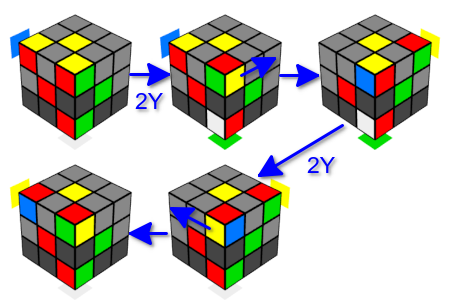
استنتاج

لا أعرف كيف سيكون الأمر في حالتك ، لكن بالنسبة لي فإن ميزة هذه الخوارزمية ليست فقط من السهل تذكرها ولا تحتاج إلى وضع تعليمات التجميع. ولكن أيضًا في حقيقة الأمر ، الآن ، بجمع المكعب ، أقوم بتجميعه بنفسي ، لفهم ما يحدث ، بدلاً من اتباع الإرشادات تقريبًا بشكل ميكانيكي ، وهذا أكثر متعة. ما اتمنى لك ايضا