في كل لعبة ورق تقريبًا بعد اللعبة ، تحتاج إلى خلط الأوراق. بينما أقوم بخلط البطاقات ، فإن السؤال الذي يطرح نفسه دائمًا هو: "هل يكفي بالفعل؟" هذا سؤال جاد - لا أريد أن أقضي الكثير من الوقت ، كما أن اللعب على سطح مشحون ليس ممتعًا أيضًا.

المادة سوف تتعامل مع الوضع.

خلط ورق اللعب الطريق

هناك طرق رائعة لتبديل البطاقات ، خلط ورق اللعب ، على سبيل المثال.

لا أعرف كيف ، ولا يمكن خلط بطاقات الكرتون بهذه الطريقة ، لذلك أنا أخلطها بطريقة بسيطة ، يبدو الأمر كما يلي:

أولاً ، أفصل الجزء عن السطح ، ثم أرمي نصيب هذا الجزء إلى الجانب الآخر ، ثم أبلغ عن الحصة المتبقية. وفقًا لملاحظاتي ، يقوم الأشخاص بتبديل البطاقات بهذه الطريقة أو بالقرب منها. بشكل عام ، يمكن تقسيمها إلى عدد أكبر من الأجزاء ، ولكن هذه هي التفاصيل بالفعل. في المقال سوف نقوم بتحليل هذه الطريقة خلط ورق اللعب.

ما هو تخطيط بطاقة عشوائية؟

أول ما حدث لي هو أنه تصميم جيد ، حيث من المحتمل أن تكون أي بطاقة في المركز الأول.

لكن هذا لا يكفي. على سبيل المثال ، إذا قمت بقطع السطح - قسمه إلى قسمين في مكان عشوائي وقم بتبديلهما - فإن البطاقة الأولى يمكن أن تكون أي فرصة. ولكن في الوقت نفسه ، من الواضح أن هذا تخطيط سيئ: بعد كل بطاقة ، باستثناء عدد قليل ، ستذهب نفس البطاقة بعدها قبل "القطع". وهذا هو ، سوف يحصل اللاعبون على بطاقات "مرتبطة". في حالة الخداع ، سيتم ضرب أحدهم ، وسيتم ضرب الآخر ، ولن يكون ذلك عرضيًا.

هناك طريقة أخرى لتحديد التصميم الجيد وهي أنه في مكان i + 1st توجد بطاقة مستقلة عن البطاقة في مكان i. يمكنك أن تتخيلها بهذه الطريقة: إذا نظرت إلى البطاقة العلوية على سطح السفينة ، لا يمكنك تخمين البطاقة التي ستكون التالية.

قد يكون لهذا النهج أيضًا مشكلات تم حلها عن طريق النظر في توزيعات مشتركة كبيرة ، ولكن بالنسبة للتحليل الحالي ، سيكون مناسبًا تمامًا لنا.

كيفية قياس "الخير" للتخطيط

أخذنا السطح المتبقي من اللعبة السابقة. نحن عدد جميع البطاقات بالترتيب. الوضع السيئ هو أنه بعد خلط في مكان ما بعد البطاقة مع رقم i هناك بطاقة مع رقم i + 1. لذلك ، سوف نقيس نسبة البطاقات التي يتم ترتيبها بعد خلط الأوراق.

def next_stat(a): c_next = 0 c_total = 0 for i in range(len(a)-1): c_total += 1 c_next += a[i] == (a[i+1]-1) return c_next * 1.0 / c_total 

من الواضح أنه حتى على سطح السفينة المزدحمة جيدًا ، ستنخفض بعض البطاقات بشكل عشوائي. ستكون حصتها في المتوسط ​​1 / (n-1) ، حيث n هو عدد البطاقات في المجموعة.

النتائج

نحن نحسب احتمال البطاقات المتتالية لمجموعة من 52 بطاقة ، وهذا يتوقف على عدد من خلط التكرارات.

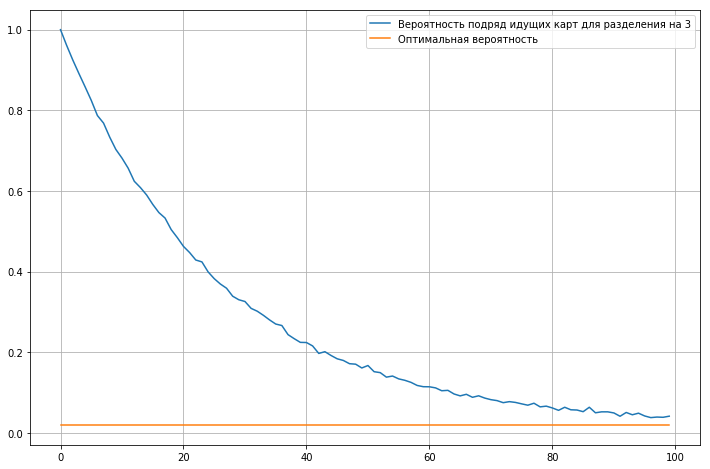
يوضح الرسم البياني أنه حتى بعد مئات التكرارات ، فإن احتمال البطاقات المتتالية يزيد بحوالي الضعف عن الاحتمال المثالي.

 import random def two_split_shuffle(a): s1 = random.randint(1,len(a)-1) s2 = random.randint(1,len(a)-1) s_min = min(s1, s2) s_max = max(s1, s2) p1 = a[:s_min] p2 = a[s_min:s_max] p3 = a[s_max:] return p3 + p2 + p1 def shuffle_n(a, f, n): for _ in range(n): a = f(a) return a def next_stat(a): c_next = 0 c_total = 0 for i in range(len(a)-1): c_total += 1 c_next += a[i] == (a[i+1]-1) return c_next * 1.0 / c_total def expected(f, n = 100): s = 0 for _ in range(n): s += f() return s / n def get_expected_next_stat(shuf, n, cards): return expected(lambda: next_stat(shuffle_n(range(cards), shuf, n))) cards = 52 x = range(100) y = map(lambda i: get_expected_next_stat(two_split_shuffle, i, cards), x) import matplotlib.pyplot as plt %matplotlib inline plt.figure(figsize=(12,8)) plt.plot(x, y, label = u'       3') plt.plot(x, [1./(cards-1)] * len(x), label = u' ') plt.grid() plt.legend() 

بشكل عام ، يمكننا أن نفترض أن 60 تكرارًا هي الكمية المثلى ، وأقلها سيئة بالتأكيد. أفعل حوالي 16-17 التكرار في 30 ثانية. هذا يعني أنه في حالة خلط ورق اللعب العادي ، سيستغرق الأمر دقيقتين تقريبًا .

أنا وأصدقائي لن أخلط البطاقات كثيرًا. وهذا يعني أن لعبتنا تتأثر كثيرًا بتوازن اللعبة الأخيرة.

كن حذرا :)