طرق Newton-Cotes هي مزيج من تقنيات التكامل التقريبية القائمة على:
- تقسيم الفاصل الزمني للتكامل إلى فواصل زمنية متساوية ؛
- تقريب integrand على فترات مختارة من متعددو الحدود.
- العثور على المساحة الإجمالية للرباعي المنحني الذي تم الحصول عليه.
سوف تغطي هذه المقالة العديد من أساليب نيوتن كوتس:
- شبه منحرف طريقة؛
- طريقة سيمبسون
- طريقة رومبرج.
شبه منحرف الطريقة
طريقة شبه منحرف هي أبسط من تلك النظر فيها. كمثال ، خذ المكمل التالي:
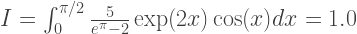
تعتمد دقة التقريب على عدد N للقطاعات التي يتم تقسيم فاصل التكامل عليها. وبالتالي ، فإن طول الفجوة:
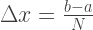
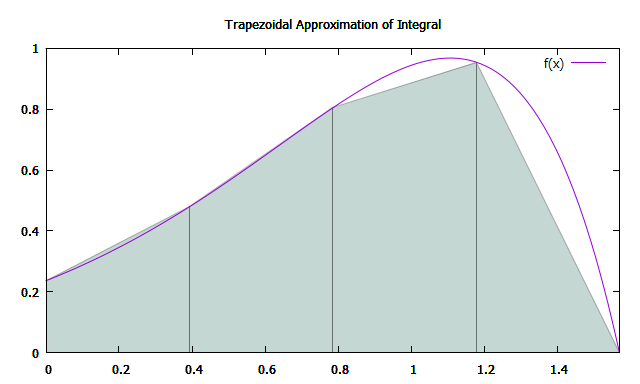
يمكن حساب مساحة شبه المنحرف من خلال الصيغة:
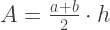
تلخيص كل ما سبق ، يتم حساب القيمة التقريبية للتكامل بالمعادلة:
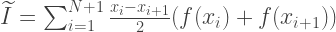
يجب أن تأخذ الدالة التي تحسب التكامل بواسطة طريقة شبه المنحرف 4 معلمات:
- حدود قطاع التكامل ؛
- وظيفة متكاملة
- عدد N للفواصل الزمنية للقسم.
double trapezoidalIntegral(double a, double b, int n, const std::function<double (double)> &f) { const double width = (ba)/n; double trapezoidal_integral = 0; for(int step = 0; step < n; step++) { const double x1 = a + step*width; const double x2 = a + (step+1)*width; trapezoidal_integral += 0.5*(x2-x1)*(f(x1) + f(x2)); } return trapezoidal_integral; }
طريقة سيمبسون
تتكون طريقة سيمبسون من تكامل متعدد الحدود من الدرجة الثانية للدالة f (x) مع عقد الاستيفاء a و b و m = (a + b) / 2 - parabolas p (x). لزيادة الدقة ، من المنطقي تقسيم جزء التكامل إلى فواصل زمنية متساوية ( عن طريق القياس مع طريقة شبه المنحرف) ، على كل منها تطبيق طريقة سيمبسون.
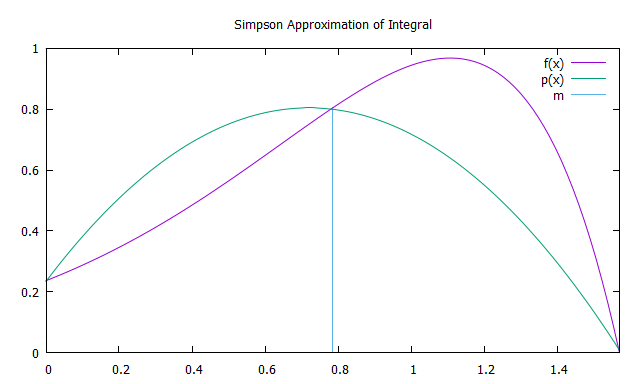
يمكن العثور على مساحة القطع المكافئة عن طريق جمع مساحات 6 مستطيلات متساوية العرض. يجب أن يكون ارتفاع أولهم مساوياً لـ f (a) ، من الثالث إلى الخامس - f (m) ، السادس - f (m). وبالتالي ، يتم العثور على التقريب بواسطة أسلوب Simpson بواسطة الصيغة:
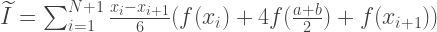
double simpsonIntegral(double a, double b, int n, const std::function<double (double)> &f) { const double width = (ba)/n; double simpson_integral = 0; for(int step = 0; step < n; step++) { const double x1 = a + step*width; const double x2 = a + (step+1)*width; simpson_integral += (x2-x1)/6.0*(f(x1) + 4.0*f(0.5*(x1+x2)) + f(x2)); } return simpson_integral; }
طريقة رومبرج
دع T (x) هو التقريب الكامل الذي تم الحصول عليه بواسطة طريقة شبه المنحرف مع الخطوة x. نحصل على 3 تقريبات من هذا القبيل ، مما يقلل من حجم الخطوة بمقدار 2 مرات مع كل حساب.

نقوم الآن ببناء مكافئ مكافئ فيما يتعلق بالمحور y ، مروراً بالنقطتين T (1) و T (1/2) لاستنباط القيم التي تم الحصول عليها ل x تميل إلى 0.
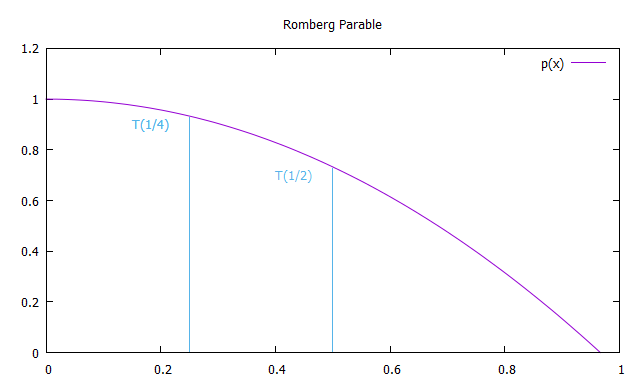
لذلك ، كل عضو في العمود الأول R (n ، 0) من تقريبات Romberg يكافئ الحلول التي تم الحصول عليها بواسطة الطريقة شبه المنحرف ، وكل حل في العمود الثاني من R (n ، 1) مكافئ لطريقة Simpson. وبالتالي ، فإن صيغ التكامل التقريبي بطريقة رومبرغ:
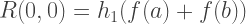
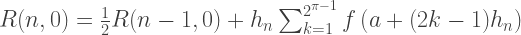
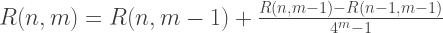
تنفيذ C ++:
std::vector<std::vector<double>> rombergIntegral(double a, double b, size_t n, const std::function<double (double)> &f) { std::vector<std::vector<double>> romberg_integral(n, std::vector<double>(n)); romberg_integral.front().front() = trapezoidalIntegral(a, b, 1, f); double h = ba; for(size_t step = 1; step < n; step++) { h *= 0.5; double trapezoidal_integration = 0; size_t stepEnd = pow(2, step - 1); for(size_t tzStep = 1; tzStep <= stepEnd; tzStep++) { const double deltaX = (2*tzStep - 1)*h; trapezoidal_integration += f(a + deltaX); } romberg_integral[step].front() = 0.5*romberg_integral[step - 1].front() + trapezoidal_integration*h; for(size_t rbStep = 1; rbStep <= step; rbStep++) { const double k = pow(4, rbStep); romberg_integral[step][rbStep] = (k*romberg_integral[step][rbStep-1] - romberg_integral[step-1][rbStep-1])/(k-1); } } return romberg_integral; }