نأتي معادلة الانحدار الخطي في شكل مصفوفة

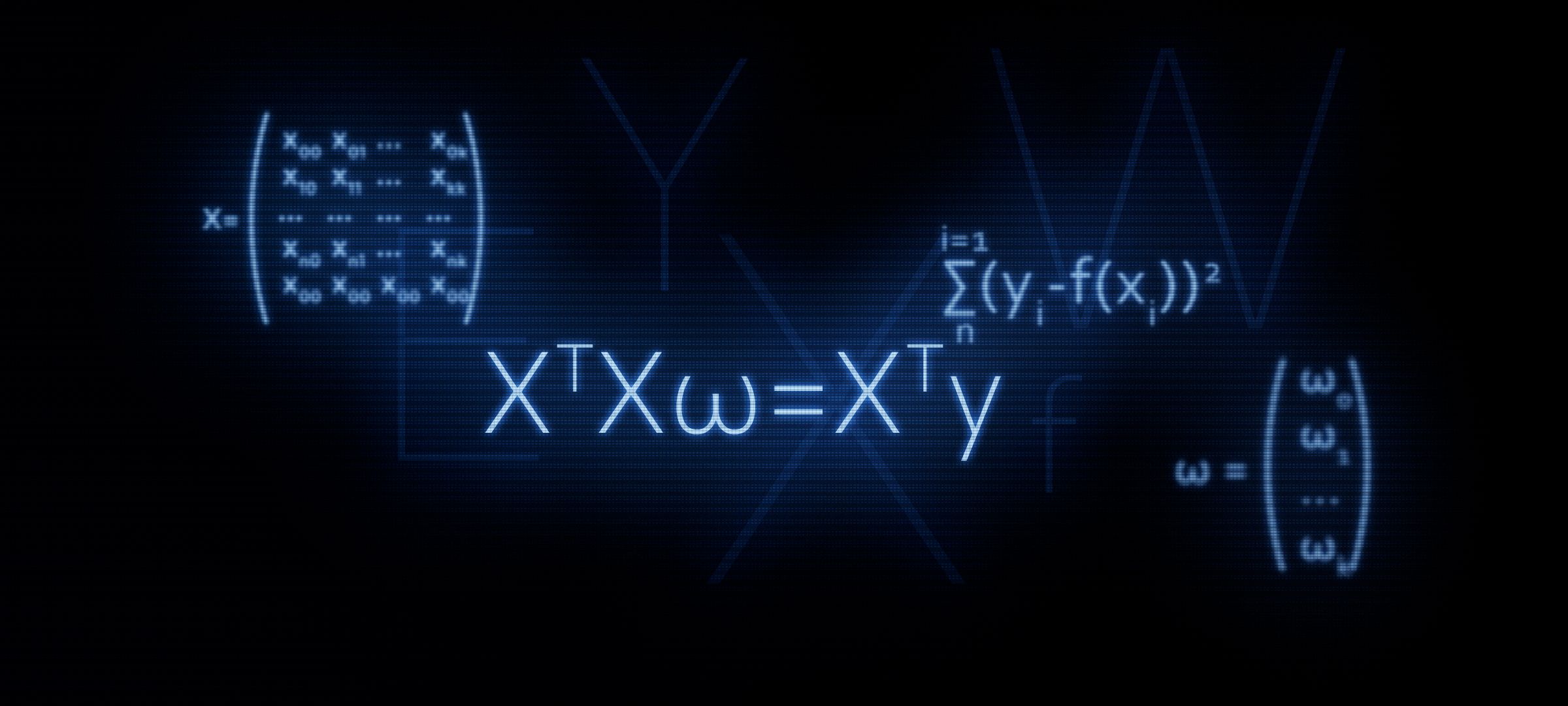
الغرض من المقالة هو توفير الدعم لمديري بيانات المبتدئين. في المقالة السابقة ، درسنا على الأصابع ثلاث طرق لحل معادلة الانحدار الخطي: حل تحليلي ، أصل متدرج ، أصل تدرج عشوائي. ثم من أجل الحل التحليلي طبقنا الصيغة $$$X ^ T X \ vec {w} = X ^ T \ vec {y}$ . في هذه المقالة ، على النحو التالي من العنوان ، سنبرر استخدام هذه الصيغة ، أو بمعنى آخر ، سوف نستمدها بشكل مستقل.

لماذا يكون من المنطقي إيلاء المزيد من الاهتمام لهذه الصيغة $$$X ^ T X \ vec {w} = X ^ T \ vec {y}$ ؟

مع معادلة المصفوفة ، يبدأ التعارف الخطي في معظم الحالات. في الوقت نفسه ، الحسابات التفصيلية لكيفية اشتقاق الصيغة نادرة.

على سبيل المثال ، في دورات Yandex للتعلم الآلي ، عندما يتم تعريف الطلاب على التنظيم ، يقترحون استخدام الوظائف من مكتبة sklearn ، بينما لم يتم ذكر كلمة حول تمثيل المصفوفة للخوارزمية. في هذه اللحظة ، قد يرغب بعض المستمعين في فهم هذه المشكلة بمزيد من التفصيل - كتابة التعليمات البرمجية دون استخدام وظائف جاهزة. ولهذا ، يجب أولاً تقديم المعادلة مع المنظم في شكل مصفوفة. هذه المادة سوف تسمح لأولئك الذين يرغبون في إتقان هذه المهارات. لنبدأ.

الظروف الأولية

أهداف

لدينا عدد من القيم المستهدفة. على سبيل المثال ، قد يكون الهدف هو سعر الأصل: النفط ، الذهب ، القمح ، الدولار ، إلخ. في الوقت نفسه ، نعني بعدد من قيم المؤشر الهدف عدد المشاهدات. قد تكون هذه الملاحظات ، على سبيل المثال ، أسعار النفط الشهرية لهذا العام ، أي أنه سيكون لدينا 12 قيمة مستهدفة. نبدأ في تقديم التدوين. نخصص كل قيمة مستهدفة $$$y_i$ . المجموع لدينا $$$ن$ الملاحظات ، مما يعني أنه يمكننا تخيل ملاحظاتنا على أنها $$$y_1 ، y_2 ، y_3 ... y_n$ .

regressors

نحن نفترض أن هناك عوامل تفسر إلى حد ما قيم المؤشر المستهدف. على سبيل المثال ، يتأثر سعر صرف زوج الدولار / الروبل بشدة بسعر النفط ، وسعر بنك الاحتياطي الفيدرالي ، وما إلى ذلك. وتسمى هذه العوامل عوامل التراجع. في الوقت نفسه ، يجب أن تتوافق كل قيمة من المؤشر المستهدف مع قيمة المراجع ، أي إذا كان لدينا 12 هدفًا لكل شهر في عام 2018 ، فيجب أن يكون لدينا أيضًا 12 من التراجعات لنفس الفترة. تدل على قيم كل ريتور بواسطة $$$x_i: x_1 ، x_2 ، x_3 ... x_n$ . دع في حالتنا هناك $$$ك$ التراجع (أي $$$ك$ العوامل التي تؤثر على قيمة الهدف). لذلك يمكن تمثيل التراجعات الخاصة بنا على النحو التالي: بالنسبة للتراجع الأول (على سبيل المثال ، سعر النفط): $$$x_ {11} ، x_ {12} ، x_ {13} ... x_ {1n}$ بالنسبة إلى التراجع الثاني (على سبيل المثال ، معدل الاحتياطي الفيدرالي): $$$x_ {21} ، x_ {22} ، x_ {23} ... x_ {2n}$ ل" $$$ك$ ال "التراجع: $$$x_ {k1}، x_ {k2}، x_ {k3} ... x_ {kn}$

اعتماد الأهداف على التراجع

تفترض التبعية الهدف $$$y_i$ من التراجع " $$$i$ - يمكن التعبير عن "الملاحظة" من خلال معادلة الانحدار الخطي للشكل:

$$

$$f (w، x_i) = w_0 + w_1 x_ {1i} + ... + w_k x_ {ki}$$

حيث $$$x_i$ - " $$$i$ ال "قيمة التراجع من 1 إلى $$$ن$ .

$$$ك$ - عدد النواقص من 1 إلى $$$ك$

$$$w$ - المعاملات الزاوية التي تمثل المقدار الذي سيتغير به المؤشر الهدف المحسوب في المتوسط ​​عندما يتغير التراجع.

وبعبارة أخرى ، نحن للجميع (باستثناء $$$w_0 دولا$ ) من التراجع نحدد معامل "لدينا" $$$w$ ، ثم اضرب المعاملات بقيم التراجع " $$$i$ - "الملاحظة ، ونتيجة لذلك نحصل على تقريب معين" $$$i$ ال "الهدف.

لذلك ، نحن بحاجة إلى تحديد هذه المعاملات $$$w$ التي قيم وظيفة تقريب لدينا $$$f (w ، x_i)$ سيكون موجودا في أقرب وقت ممكن لقيم الأهداف.

تقدير جودة الوظيفة التقريبية

سنحدد تقدير الجودة لوظيفة التقريب بأسلوب المربعات الصغرى. ستتخذ وظيفة تقييم الجودة في هذه الحالة النموذج التالي:

$$

$$Err = \ sum \ limit_ {i = 1} ^ n (y_i-f (x_i)) ^ 2 \ rightarrow min$$

نحن بحاجة إلى اختيار هذه القيم للمعاملات $ w $ التي القيمة $$ سيكون أصغر.

نترجم المعادلة إلى شكل مصفوفة

ناقلات الرأي

أولاً ، لجعل حياتك أسهل ، يجب الانتباه إلى معادلة الانحدار الخطي ولاحظ أن المعامل الأول $$$w_0 دولا$ لا مضروبة في أي التراجع. علاوة على ذلك ، عندما نترجم البيانات إلى شكل مصفوفة ، فإن الظرف أعلاه سيعقد العمليات الحسابية بشكل خطير. في هذا الصدد ، يُقترح إدخال مُراجع آخر للمعامل الأول $$$w_0 دولا$ وتساوي واحد. أو بالأحرى ، كل " $$$i$ "قيمة" هذا التراجع تساوي الوحدة - لأنه عند ضرب الوحدة ، لن يتغير شيء من حيث نتيجة الحسابات ، ومن وجهة نظر القواعد الخاصة بمنتج المصفوفات ، سيتم تقليل عذابنا بشكل كبير.

الآن ، لفترة من الوقت ، لتبسيط المواد ، لنفترض أن لدينا واحدة فقط " $$$i$ ال "ملاحظة. ثم ، تخيل قيم التراجع" $$$i$ ال عشر كما ناقلات $$$\ vec {x_i}$ . سهم التوجيه $$$\ vec {x_i}$ لديه البعد $$$(ك \ مرات 1)$ هذا هو $$$ك$ الصفوف والعمود 1:

$$

$$\ vec {x_i} = \ تبدأ {pmatrix} x_ {0i} \\ x_ {1i} \\ ... \\ x_ {ki} \ end {pmatrix} \ qquad$$

يمكن تمثيل المعاملات المطلوبة باعتبارها ناقلات $$$\ vec {w}$ وجود البعد $$$(ك \ مرات 1)$ :

$$

$$\ vec {w} = \ تبدأ {pmatrix} w_0 \\ w_1 \\ ... \\ w_k \ end {pmatrix} \ qquad$$

معادلة الانحدار الخطي لـ " $$$i$ - الملاحظة "سوف تأخذ الشكل:

$$

$$f (w، x_i) = \ vec {x_i} ^ T \ vec {w}$$

ستتخذ وظيفة تقييم الجودة للنموذج الخطي الشكل التالي:

$$

$$Err = \ sum \ limit_ {i = 1} ^ n (y_i- \ vec {x_i} ^ T \ vec {w}) ^ 2 \ rightarrow min$$

لاحظ أنه وفقًا لقواعد ضرب المصفوفة ، نحتاج إلى نقل المتجه $$$\ vec {x_i}$ .

تمثيل المصفوفة

نتيجة لضرب المتجهات ، نحصل على الرقم: $$$(1 \ times k) \ centerdot (k \ times 1) = 1 \ times 1$ كما هو متوقع. هذا الرقم هو تقريب " $$$i$ "الهدف. لكننا بحاجة إلى تقريب قيمة واحدة من الهدف ، ولكن كل شيء. للقيام بهذا ، نكتب كل شيء" $$$i$ مصفوفات التراجع $$$X$ . المصفوفة الناتجة لها البعد $$$(ن \ مرات ك)$ :

$$عرض $$ $ X = \ تبدأ {pmatrix} x_ {00} & x_ {01} & ... & x_ {0k} \\ x_ {10} & x_ {11} & ... & x_ {1k} \\ ... & ... & ... & ... \\ x_ {n0} & x_ {n1} & ... & x_ {nk} \ end {pmatrix} \ qquad $$ عرض $$

الآن سوف تأخذ معادلة الانحدار الخطي الشكل:

$$

$$f (w، X) = X \ vec {w}$$

تشير إلى قيم المؤشرات المستهدفة (الكل $$$y_i$ ) لكل متجه $$$\ vec {y}$ الأبعاد $$$(ن \ مرة 1)$ :

$$

$$\ vec {y} = \ start {pmatrix} y_ {0} \\ y_ {1} \\ ... \\ y_ {n} \ end {pmatrix} \ qquad$$

الآن يمكننا أن نكتب في نسق المصفوفة المعادلة لتقييم جودة النموذج الخطي:

$$

$$Err = (X \ vec {w} - \ vec {y}) ^ 2 \ rightarrow min$$

في الواقع ، من هذه الصيغة نحصل على الصيغة المعروفة لنا $$$X ^ T X w = X ^ T y$

كيف يتم ذلك؟ يتم فتح الأقواس ، ويتم تنفيذ التمايز ، ويتم تحويل التعبيرات الناتجة ، وما إلى ذلك ، وهذا ما سنفعله الآن.

التحولات المصفوفة

توسيع الأقواس

$$$(X \ vec {w} - \ vec {y}) ^ 2 = (X \ vec {w} - \ vec {y}) ^ T (X \ vec {w} - \ vec {y})$

$$$= (X \ vec {w}) ^ TX \ vec {w} - \ vec {y} ^ TX \ vec {w} - (X \ vec {w}) ^ T \ vec {y} + \ \ vec { y} ^ T \ vec {y}$

إعداد معادلة للتمايز

للقيام بذلك ، نقوم ببعض التحولات. في الحسابات اللاحقة ، سيكون أكثر ملاءمة لنا إذا كان المتجه $$$\ vec {w} ^ T$ سيتم تقديمه في بداية كل عمل في المعادلة.

التحويل 1

$$$\ vec {y} ^ TX \ vec {w} = (X \ vec {w}) ^ T \ vec {y} = \ vec {w} ^ TX ^ T \ vec {y}$

كيف حدث هذا؟ للإجابة على هذا السؤال ، فقط انظر إلى أحجام المصفوفات المضروبة وشاهد أنه في المخرجات نحصل على رقم أو غير ذلك $$$const$ .

نكتب أبعاد تعبيرات المصفوفة.

$$$\ vec {y} ^ TX \ vec {w}: (1 \ times n) \ centerdot (n \ times k) \ centerdot (k \ times 1) = (1 \ times 1) = const$

$$$(X \ vec {w}) ^ T \ vec {y}: ((n \ times k) \ centerdot (k \ times 1)) ^ T \ centerdot (n \ times 1) = (1 \ times n) \ centerdot (n \ times 1) = (1 \ times 1) = const$

$$$\ vec {w} ^ TX ^ T \ vec {y}: (1 \ times k) \ centerdot (k \ times n) \ centerdot (n \ times 1) = (1 \ times 1) = const$

التحويل 2

$$$(X \ vec {w}) ^ TX \ vec {w} = \ vec {w} ^ TX ^ TX \ vec {w}$

نكتب بالمثل التحول 1

$$$(X \ vec {w}) ^ TX \ vec {w}: ((n \ times k) \ centerdot (k \ times 1)) ^ T \ centerdot (n \ times k) \ centerdot (k \ times 1 ) = (1 \ مرة 1) = const$

$$$\ vec {w} ^ TX ^ TX \ vec {w}: (1 \ times k) \ centerdot (k \ times n) \ centerdot (n \ times k) \ centerdot (k \ times 1) = (1 \ مرات 1) = const$

في المخرجات ، نحصل على معادلة يجب أن نفرقها:
$$$Err = \ vec {w} ^ TX ^ TX \ vec {w} - 2 \ vec {w} ^ TX ^ T \ vec {y} + \ vec {y} ^ T \ vec {y}$

نحن نفرق بين وظيفة تقييم جودة النموذج

التفريق بواسطة ناقل $$$\ vec {w}$ :

$$

$$\ frac {d (\ vec {w} ^ TX ^ TX \ vec {w} - 2 \ vec {w} ^ TX ^ T \ vec {y} + \ vec {y} ^ T \ vec {y}) } {d \ vec {w}}$$

$$$(\ vec {w} ^ TX ^ TX \ vec {w}) '- (2 \ vec {w} ^ TX ^ T \ vec {y})' + (\ vec {y} ^ T \ vec {y }) '= 0$

$$$2X ^ TX \ vec {w} - 2X ^ T \ vec {y} + 0 = 0$

$$$X ^ TX \ vec {w} = X ^ T \ vec {y}$

أسئلة لماذا $$$(\ vec {y} ^ T \ vec {y}) '= 0$ لا ينبغي أن يكون ، ولكن العمليات لتحديد المشتقات في التعبيرات الأخرى ، سنحلل بمزيد من التفصيل.

التمايز 1

نكشف التمايز: $$$\ frac {d (\ vec {w} ^ TX ^ TX \ vec {w})} {d \ vec {w}} = 2X ^ TX \ vec {w}$

من أجل تحديد مشتق مصفوفة أو متجه ، تحتاج إلى معرفة ما لديهم في الداخل. نحن ننظر:

$$$ inline $ \ vec {w} ^ T = \ تبدأ {pmatrix} w_0 & w_1 & ... & w_k \ end {pmatrix} \ qquad $ inline $

$$$\ vec {w} = \ تبدأ {pmatrix} w_0 \\ w_1 \\ ... \\ w_k \ end {pmatrix} \ qquad$

$$$ inline $ X ^ T = \ start {pmatrix} x_ {00} & x_ {10} & ... & x_ {n0} \\ x_ {01} & x_ {11} & ... & x_ {n1} \\ ... & ... & ... & ... \\ x_ {0k} & x_ {1k} & ... & x_ {nk} \ end {pmatrix} \ qquad $ inline $$$ $ inline $ X = \ تبدأ {pmatrix} x_ {00} & x_ {01} & ... & x_ {0k} \\ x_ {10} & x_ {11} & ... & x_ {1k} \\ ... & ... & ... & ... \\ x_ {n0} & x_ {n1} & ... & x_ {nk} \ end {pmatrix} \ qquad $ inline $

تشير إلى المنتج من المصفوفات $$$X ^ TX$ من خلال المصفوفة $$$دولا$ . قالب $$$دولا$ مربع وعلاوة على ذلك ، فمن متماثل. هذه الخصائص ستكون مفيدة لنا أكثر ، تذكرها. قالب $$$دولا$ لديه البعد $$$(ك \ مرات ك)$ :

$$$ inline $ A = \ تبدأ {pmatrix} a_ {00} & a_ {01} & ... & a_ {0k} \\ a_ {10} & a_ {11} & ... & a_ {1k} \\ ... & ... & ... & ... \\ a_ {k0} & a_ {k1} & ... & a_ {kk} \ end {pmatrix} \ qquad $ inline $

الآن مهمتنا هي مضاعفة المتجهات بشكل صحيح من خلال المصفوفة وعدم الحصول على "مرتين خمسة خمسة" ، لذلك سنركز ونكون حذرين للغاية.

$$$ inline $ \ vec {w} ^ TA \ vec {w} = \ تبدأ {pmatrix} w_0 & w_1 & ... & w_k \ end {pmatrix} \ qquad \ times \ تبدأ {pmatrix} a_ {00} & a_ {01} & ... & a_ {0k} \\ a_ {10} & a_ {11} & ... & a_ {1k} \\ ... & ... & ... & ... \ \ a_ {k0} & a_ {k1} & ... & a_ {kk} \ end {pmatrix} \ qquad \ times \ تبدأ {pmatrix} w_0 \\ w_1 \\ ... \\ w_k \ end {pmatrix} \ qquad = $ inline $

$$$ inline $ = \ تبدأ {pmatrix} w_0a_ {00} + w_1a_ {10} + ... + w_ka_ {k0} & ... & w_0a_ {0k} + w_1a_ {1k} + ... + w_ka_ {kk} \ end {pmatrix} \ times \ تبدأ {pmatrix} w_0 \\ w_1 \\ ... \\ w_k \ end {pmatrix} \ qquad = $ inline $

$$$= \ تبدأ {pmatrix} (w_0a_ {00} + w_1a_ {10} + ... + w_ka_ {k0}) w_0 \ mkern 10mu + \ \ mkern 10mu ... \ mkern 10mu + \ mkern 10mu (w_0a_ {0k} + w_1a_ {1k} + ... + w_ka_ {kk}) w_k \ end {pmatrix} =$

$$$= w_0 ^ 2a_ {00} + w_1a_ {10} w_0 + w_ka_ {k0} w_0 \ mkern 10mu + \ mkern 10mu ... \ mkern 10mu + \ mkern 10mu w_0a_ {0k} $ . + w_k ^ 2a_ {kk}$

ومع ذلك ، حصلنا على تعبير معقد! في الواقع ، حصلنا على رقم - عددية. والآن ، بالفعل بالفعل ، نمر بالتمييز. من الضروري إيجاد مشتق التعبير الذي تم الحصول عليه لكل معامل $$$w_0 w_1 ... w_k$ والحصول على ناقل البعد في الإخراج $$$(ك \ مرات 1)$ . فقط في حالة ، سوف أصف إجراءات الإجراءات:

1) التفريق من قبل $$$w_o$ حصلنا على: $$$2w_0a_ {00} + w_1a_ {10} + w_2a_ {20} + ... + w_ka_ {k0} + a_ {01} w_1 + a_ {02} w_2 + ... + a_ {0k} w_ {k}$

2) التفريق من قبل $$$w_1$ حصلنا على: $$$w_0a_ {01} + 2w_1a_ {11} + w_2a_ {21} + ... + w_ka_ {k1} + a_ {10} w_0 + a_ {12} w_2 + ... + a_ {1k} w_ {k}$

3) التفريق من قبل $$$w_k$ حصلنا على: $$$w_0a_ {0k} + w_1a_ {1k} + w_2a_ {2k} + ... + w _ {(k-1)} a _ {(k-1) k} + a_ {k0} w_0 + a_ {k1} w_1 + a_ {k2} w_2 + ... + 2w_ka_ {kk}$

في الإخراج ، ناقلات وعدت حجمها $$$(ك \ مرات 1)$ :

$$

$$\ تبدأ {pmatrix} 2w_0a_ {00} + w_1a_ {10} + w_2a_ {20} + ... + w_ka_ {k0} + a_ {01} w_1 + a_ {02} w_2 + ... + a_ {0k} w_ {k} \\ w_0a_ {01} + 2w_1a_ {11} + w_2a_ {21} + ... + w_ka_ {k1} + a_ {10} w_0 + a_ {12} w_2 + ... + a_ {1k} w_ { k} \\ ... \\ ... \\ ... \\ w_0a_ {0k} + w_1a_ {1k} + w_2a_ {2k} + ... + w _ {(k-1)} a _ {(k -1) k} + a_ {k0} w_0 + a_ {k1} w_1 + a_ {k2} w_2 + ... + 2w_ka_ {kk} \ end {pmatrix}$$

إذا ألقيت نظرة فاحصة على المتجه ، ستلاحظ أن العناصر اليمنى واليسرى المقابلة من المتجه يمكن تجميعها بطريقة ، ونتيجة لذلك ، يمكن تمييز المتجه عن المتجه المقدم $$$\ vec {w}$ الحجم $$$(ك \ مرات 1)$ . على سبيل المثال $$$w_1a_ {10}$ (العنصر الأيسر من السطر العلوي للمتجه) $$$+ a_ {01} w_1$ (يمكن تمثيل العنصر الأيمن من السطر العلوي من المتجه) كـ $$$w_1 (a_ {10} + a_ {01})$ و $$$w_2a_ {20} + a_ {02} w_2$ - كيف $$$w_2 (a_ {20} + a_ {02})$ إلخ على كل سطر. مجموعة نحن:

$$

$$\ تبدأ {pmatrix} 2w_0a_ {00} + w_1 (a_ {10} + a_ {01}) + w_2 (a_ {20} + a_ {02}) + ... + w_k (a_ {k0} + a_ { 0k}) \\ w_0 (a_ {01} + a_ {10}) + 2w_1a_ {11} + w_2 (a_ {21} + a_ {12}) + ... + w_k (a_ {k1} + a_ {1k }) \\ ... \\ ... \\ ... \\ w_0 (a_ {0k} + a_ {k0}) + w_1 (a_ {1k} + a_ {k1}) + w_2 (a_ {2k } + a_ {k2}) + ... + 2w_ka_ {kk} \ end {pmatrix}$$

اخراج المتجه $$$\ vec {w}$ وفي الإخراج نحصل على:

$$عرض $$ $$ \ تبدأ {pmatrix} 2a_ {00} & a_ {10} + a_ {01} & a_ {20} + a_ {02} & ... & a_ {k0} + a_ {0k} \\ a_ {01} + a_ {10} & 2a_ {11} & a_ {21} + a_ {12} & ... & a_ {k1} + a_ {1k} \\ ... & ... & .. . & ... & ... \\ ... & ... & ... & ... & ... \\ ... & ... & ... & .. . \\ a_ {0k} + a_ {k0} & a_ {1k} + a_ {k1} & a_ {2k} + a_ {k2} & ... & 2a_ {kk} \ end {pmatrix} \ times \ تبدأ {pmatrix} w_0 \\ w_1 \\ ... \\ ... \\ ... \\ w_k \ end {pmatrix} \ qquad $$ عرض $$

الآن ، دعونا نلقي نظرة على المصفوفة الناتجة. المصفوفة هي مجموع المصفوفات اثنين $$$A + A ^ T$ :

$$عرض $$ $$ \ تبدأ {pmatrix} a_ {00} & a_ {01} & a_ {02} & ... & a_ {0k} \\ a_ {10} & a_ {11} & a_ {12} & ... & a_ {1k} \\ ... & ... & ... & ... & ... \\ a_ {k0} & a_ {k1} & a_ {k2} & ... & a_ {kk} \ end {pmatrix} + \ start {pmatrix} a_ {00} & a_ {10} & a_ {20} & ... & a_ {k0} \\ a_ {01} & a_ {11} & a_ {21} & ... & a_ {k1} \\ ... & ... & ... & ... & ... \\ a_ {0k} & a_ {1k} & a_ {2k} & ... & a_ {kk} \ end {pmatrix} \ qquad $$ عرض $$

أذكر أنه في وقت سابق قليلا ، لاحظنا خاصية واحدة مهمة للمصفوفة $$$دولا$ - إنه متماثل. بناءً على هذه الخاصية ، يمكننا أن نقول بثقة أن التعبير $$$A + A ^ T$ متساوين $$$2A$ . هذا سهل التحقق من خلال الكشف عن المنتج المصفوفة حسب العنصر $$$X ^ TX$ . لن نفعل ذلك هنا ، يمكن لأولئك الذين يرغبون في إجراء التحقق بأنفسهم.

دعنا نعود إلى تعبيرنا. بعد تحولاتنا ، اتضح كما أردنا رؤيته:

$$

$$(A + A ^ T) \ times \ تبدأ {pmatrix} w_0 \\ w_1 \\ ... \\ w_k \ end {pmatrix} \ qquad = 2A \ vec {w} = 2X ^ TX \ vec {w}$$

لذلك ، تعاملنا مع التمايز الأول. نمر إلى التعبير الثاني.

التمايز 2

$$$\ frac {d (2 \ vec {w} ^ TX ^ T \ vec {y})} {d \ vec {w}} = 2X ^ T \ vec {y}$

دعنا نذهب على طول الطريق المطروق. سيكون أقصر بكثير من السابق ، لذلك لا تذهب بعيدا عن الشاشة.

نكشف عن ناقلات المصفوفة والعناصر الحكيمة:

$$$ inline $ \ vec {w} ^ T = \ تبدأ {pmatrix} w_0 & w_1 & ... & w_k \ end {pmatrix} \ qquad $ inline $

$$$ inline $ X ^ T = \ start {pmatrix} x_ {00} & x_ {10} & ... & x_ {n0} \\ x_ {01} & x_ {11} & ... & x_ {n1} \\ ... & ... & ... & ... \\ x_ {0k} & x_ {1k} & ... & x_ {nk} \ end {pmatrix} \ qquad $ inline $

$$$\ vec {y} = \ تبدأ {pmatrix} y_0 \\ y_1 \\ ... \\ y_n \ end {pmatrix} \ qquad$

لفترة من الوقت ، نزيل الشيطان من الحسابات - لا يلعب دورًا كبيرًا ، ثم سنعيده إلى مكانه. اضرب المتجهات بواسطة المصفوفة. بادئ ذي بدء ، نضرب المصفوفة $$$X ^ T$ على ناقلات $$$\ vec {y}$ ، هنا ليس لدينا قيود. الحصول على ناقلات الحجم $$$(ك \ مرات 1)$ :

$$

$$\ تبدأ {pmatrix} x_ {00} y_0 + x_ {10} y_1 + ... + x_ {n0} y_n \\ x_ {01} y_0 + x_ {11} y_1 + ... + x_ {n1} y_n \\ ... \\ x_ {0k} y_0 + x_ {1k} y_1 + ... + x_ {nk} y_n \ end {pmatrix} \ qquad$$

قم بتنفيذ الإجراء التالي - اضرب المتجه $$$\ vec {w}$ إلى ناقلات الناتجة. في الخرج ، سوف ينتظرنا رقم:

$$

$$\ تبدأ {pmatrix} w_0 (x_ {00} y_0 + x_ {10} y_1 + ... + x_ {n0} y_n) + w_1 (x_ {01} y_0 + x_ {11} y_1 + ... + x_ {n1 } y_n) \ mkern 10mu + \ mkern 10mu ... \ mkern 10mu + \ mkern 10mu w_k (x_ {0k} y_0 + x_ {1k} y_1 + ... + x_ {nk} y_n) \ end {pmatrix} \ qquad$$

نحن ثم نفرق ذلك. في الإخراج نحصل على ناقل البعد $$$(ك \ مرات 1)$ :

$$

$$\ تبدأ {pmatrix} x_ {00} y_0 + x_ {10} y_1 + ... + x_ {n0} y_n \\ x_ {01} y_0 + x_ {11} y_1 + ... + x_ {n1} y_n \\ ... \\ x_ {0k} y_0 + x_ {1k} y_1 + ... + x_ {nk} y_n \ end {pmatrix} \ qquad$$

هل يشبه شيئا؟ حسنًا! هذا هو نتاج المصفوفة. $$$X ^ T$ على ناقلات $$$\ vec {y}$ .

وهكذا ، تم الانتهاء من التمايز الثاني بنجاح.

بدلا من الاستنتاج

الآن نحن نعرف كيف جاءت المساواة. $$$X ^ T X \ vec {w} = X ^ T \ vec {y}$ .

أخيرًا ، نصف طريقة سريعة لتحويل الصيغ الرئيسية.

تقدير جودة النموذج وفقًا لطريقة المربعات الصغرى:
$$$\ sum \ limit_ {i = 1} ^ n (y_i-f (x_i)) ^ 2 \ mkern 20mu = \ mkern 20mu \ sum \ limit_ {i = 1} ^ n (y_i- \ vec {x_i} ^ T \ vec {w}) ^ 2 =$

$$$= (X \ vec {w} - \ vec {y}) ^ 2 \ mkern 20mu = \ mkern 20mu (X \ vec {w} - \ vec {y}) ^ T (X \ vec {w} - \ vec {y}) \ mkern 20mu = \ mkern 20mu \ vec {w} ^ TX ^ TX \ vec {w} - 2 \ vec {w} ^ TX ^ T \ vec {y} + \ vec {y} ^ T \ vec {y}$

نحن نفرق بين التعبير الناتج:
$$$\ frac {d (\ vec {w} ^ TX ^ TX \ vec {w} - 2 \ vec {w} ^ TX ^ T \ vec {y} + \ vec {y} ^ T \ vec {y}) } {d \ vec {w}} =$$$$2X ^ TX \ vec {w} - 2X ^ T \ vec {y} = 0$

$$$X ^ TX \ vec {w} = X ^ T \ vec {y}$

$$$\ leftarrow$ العمل السابق للمؤلف - "نحل معادلة الانحدار الخطي البسيط"
$$$\ rightarrow$ العمل التالي للمؤلف - "مضغ الانحدار اللوجستي"

أدب

مصادر الانترنت:

1) habr.com/en/post/278513
2) habr.com/ru/company/ods/blog/322076
3) habr.com/en/post/307004
4) nabatchikov.com/blog/view/matrix_der

الكتب المدرسية ومجموعات المهام:

1) ملاحظات محاضرة في الرياضيات العليا: دورة كاملة / D.T. مكتوب - 4th الطبعة. - م: مطبعة ايريس ، 2006
2) تحليل الانحدار التطبيقي / N. Draper ، G. Smith - 2nd ed. - م: المالية والإحصاء ، 1986 (مترجم من الإنجليزية)
3) مهام حل معادلات المصفوفة:
function-x.ru/matrix_equations.html
mathprofi.ru/deistviya_s_matricami.html