الرياضيات العامة غير الآمنة في C #

لسوء الحظ ، لم يكن من السهل ترجمة اسم القبح الذي بدأته إلى اللغة الروسية. لقد فوجئت عندما وجدت أن وثائق MSDN الرسمية تستدعي "قوالب" "عامة" (على غرار قوالب C++ ، أفترض). في الطبعة الرابعة من "CLR عبر C# التي صدمتني ، Jeffrey Richter ، التي ترجمها بيتر ، تسمى الأدوية الجنيسة "التعميمات" ، والتي تعكس جوهر المفهوم بشكل أفضل. هذه المادة سوف نتحدث عن العمليات الحسابية المعممة غير آمنة في C# . بالنظر إلى أن C# ليس مخصصًا للحوسبة عالية الأداء (على الرغم من أنه قادر بالطبع على ذلك ، لكنه غير قادر على التنافس مع نفس C/C++ ) ، فإن العمليات الرياضية في BCL لا تحظى كثيرًا من الاهتمام. دعونا نحاول تبسيط العمل باستخدام أنواع حسابية أساسية باستخدام C# و CLR .

بيان المشكلة

إخلاء المسئولية : سوف تحتوي المقالة على العديد من أجزاء التعليمات البرمجية ، والتي سأوضحها مع روابط إلى المورد الرائع SharpLab ( Gi r tHub ) بواسطة Andrey Shchekin .

تتلخص معظم العمليات الحسابية بطريقة أو بأخرى في العمليات الأساسية. الجمع والطرح (الانقلاب ، النفي) ، الضرب والقسمة يمكن استكمالها بعمليات المقارنة والتحقق من المساواة. بالطبع ، يمكن تنفيذ جميع هذه الإجراءات بسهولة وببساطة على متغيرات من أي أنواع حسابية أساسية من C# . المشكلة الوحيدة هي أن C# يجب أن تعلم في وقت الترجمة أن العمليات يتم تنفيذها على أنواع محددة ، ويبدو أن كتابة طريقة تضيف بنفس القدر من الكفاءة (والشفافية) رقمين صحيحين ورقمين من الفاصلة العائمة أمر مستحيل.

دعونا نحدد رغباتنا لطريقة معممة افتراضية تقوم ببعض العمليات الرياضية البسيطة:

1. يجب أن تحتوي الطريقة على قيود نوع عامة تحمينا من محاولة إضافة (أو ضرب ، قسمة) نوعين اعتباطيين. نحن بحاجة إلى بعض القيود النوع العام.
2. لنقاء التجربة ، يجب أن تكون الأنواع المقبولة والمعادة هي نفسها. على سبيل المثال ، يجب أن يكون لدى المشغل الثنائي توقيع النموذج (T, T) => T
3. يجب أن تكون الطريقة محسنة جزئيًا على الأقل. على سبيل المثال ، الملاكمة في كل مكان غير مقبولة.

وماذا عن الجيران؟

دعنا ننظر إلى F# . لست قوياً في F# ، لكن معظم قيود C# تمليها قيود CLR ، مما يعني أن F# تعاني من نفس المشكلات. يمكنك محاولة الإعلان عن طريقة إضافة معممة صريحة وطريقة الإضافة المعتادة ومعرفة ما يقوله نظام الاستدلال من النوع F# :

 let add_gen (x : 'a) (y : 'a) = x + y let add xy = x + y add_gen 5.0 6.0 |> ignore add 5.0 6.0 |> ignore 

في هذه الحالة ، سوف تتحول كلتا الطريقتين إلى عدم التعميم ، وسوف تكون الشفرة التي تم إنشاؤها متطابقة. نظرًا لصلابة نظام النوع F# ، حيث لا توجد تحويلات ضمنية للنموذج int -> double ، بعد أول استدعاء لهذه الطرق مع معلمات النوع double (في مصطلحات C# ) ، طرق الاتصال مع معلمات أنواع أخرى (حتى مع احتمال فقد الدقة بسبب تحويل الكتابة) أكثر سوف تفشل.

تجدر الإشارة إلى أنه إذا استبدلت عامل التشغيل + بعامل تشغيل المساواة = ، ستصبح الصورة مختلفة قليلاً : تتحول كلتا الطريقتين إلى معممة (من وجهة نظر C# ) F# ويتم استدعاء أسلوب مساعد خاص ، متاح في F# لإجراء المقارنة.

 let eq_gen (x : 'a) (y : 'a) = x = y let eq xy = x = y eq_gen 5.0 6.0 |> ignore eq_gen 5 6 |> ignore eq 5.0 6.0 |> ignore eq 5 6 |> ignore 

ماذا عن Java ؟

من الصعب بالنسبة لي التحدث عن Java ، ولكن ، بقدر ما أستطيع أن أقول ، هناك أنواع مهمة ليست موجودة في الشكل المعتاد بالنسبة لنا ، ولكن لا تزال هناك أنواع بدائية . للعمل مع البدائيين في Java هناك غلافات (على سبيل المثال ، مرجع Long لـ قيمة بدائية long ) ، والتي لها Number فئة أساسي مشترك. وبالتالي ، يمكنك تعميم العمليات جزئيًا باستخدام Number ، ولكن هذا نوع مرجعي ، من غير المرجح أن يكون له تأثير إيجابي على الأداء.

تصحيح لي إذا كنت مخطئا.

C++ ؟

C++ هي لغة للغشاشين.
تمهد C++ الطريق لميزات يعتبرها البعض ... غير طبيعية .
القوالب (الملقب قوالب) ، على عكس التعميمات (الوراثة) ، هي ، بالمعنى الحرفي ، قوالب . عند الإعلان عن قالب ، يمكنك تقييد الأنواع التي يتوفر لها هذا القالب بشكل صريح. لهذا السبب ، في C++ ، على سبيل المثال ، التعليمة البرمجية التالية صالحة:

 #include <iostream> template<typename T, std::enable_if_t<std::is_arithmetic<T>::value>* = nullptr> T Add (T left, T right) { return left + right; } int main() { std::cout << Add(5, 6) << std::endl; std::cout << Add(5.0, 6.0) << std::endl; // std::cout << Add("a", "b") << std::endl; Does not compile } 

is_arithmetic ، للأسف ، يسمح لكل من char و bool كمعلمات. من ناحية أخرى ، يمكن أن يكون char مكافئًا لـ sbyte في مصطلحات C# ، على الرغم من أن الأحجام الفعلية لأنواع الأعداد الصحيحة تعتمد على مرحلة النظام الأساسي / المترجم / القمر.

لغات الطباعة الديناميكية

أخيرًا ، فكر في بضع لغات مكتوبة ديناميكيًا (ومترجمة) ، تم شحذها بواسطة الحساب. في مثل هذه اللغات ، لا يؤدي تعميم الحساب عادةً إلى حدوث مشكلات: إذا كان نوع المعلمات مناسبًا للتنفيذ ، مشروطًا ، فسيتم تنفيذ العملية ، وإلا فسوف تفشل مع حدوث خطأ.

في Python (3.7.3 × 64):

 def add (x, y): return x + y type(add(5, 6)) # <class 'int'> type(add(5.0, 6.0)) # <class 'float'> type(add('a', 'b') # <class 'str'> 

في R (3.6.1 × 64)

 add <- function(x, y) x + y # Or typeof() vctrs::vec_ptype_show(add(5, 6)) # Prototype: double vctrs::vec_ptype_show(add(5L, 6L)) # Prototype: integer vctrs::vec_ptype_show(add("5", "6")) # Error in x + y : non-numeric argument to binary operator 

على العكس من ذلك ، في عالم C #: نقوم بتقييد النوع العام للوظيفة الرياضية

لسوء الحظ ، لا يمكننا القيام بذلك. في C# تكون الأنواع البدائية أنواعًا حسب القيمة ، أي الهياكل التي ، على الرغم من أنها موروثة من System.Object (و System.ValueType ) ، لا تملك الكثير من القواسم المشتركة. القيد الطبيعي والمنطقي هو where T : struct . بدءًا من C# 7.3 لدينا where T : unmanaged قيد where T : unmanaged ، مما يعني أن T هو , null . بالإضافة إلى الأنواع الحسابية البدائية التي نحتاجها ، char ، bool ، decimal ، أي Enum وأي بنية تحتوي جميع حقولها على نفس النوع unmanaged تفي بهذه المتطلبات. أي هذا النوع سوف يجتاز الاختبار:

 public struct Coords<T> where T : unmanaged { public TX; public TY; } 

وبالتالي ، لا يمكننا كتابة وظيفة معممة تقبل فقط الأنواع الحسابية المطلوبة. ومن هنا Unsafe في عنوان المقال - سنضطر إلى الاعتماد على المبرمجين باستخدام رمزنا. محاولة استدعاء الأسلوب المعمم الافتراضي T Add<T>(T left, T right) where T : unmanaged إلى نتائج غير متوقعة إذا قام المبرمج بتمرير كائنات من نوع غير متوافق كوسائط.

التجربة الأولى ، ساذجة: dynamic

dynamic هي الأداة الأولى والواضحة التي يمكن أن تساعدنا في حل مشكلتنا. بطبيعة الحال ، فإن استخدام dynamic لإجراء العمليات الحسابية أمر لا طائل منه على الإطلاق - dynamic مكافئة object ، ويتم تحويل الأساليب التي يطلق عليها المتغير dynamic إلى انعكاس وحشي من قبل المترجم. كمكافأة - تعبئة / تفريغ أنواعنا ذات القيمة. هنا مثال :

 public class Class { public static void Method() { var x = Add(5, 6); var y = Add(5.0, 6.0); } private static dynamic Add(dynamic left, dynamic right) => left + right; } 

مجرد إلقاء نظرة على IL Method الأسلوب:

 .method public hidebysig static void Method () cil managed { // Method begins at RVA 0x2050 // Code size 53 (0x35) .maxstack 8 IL_0000: ldc.i4.5 IL_0001: box [System.Private.CoreLib]System.Int32 IL_0006: ldc.i4.6 IL_0007: box [System.Private.CoreLib]System.Int32 IL_000c: call object Class::Add(object, object) IL_0011: pop IL_0012: ldc.r8 5 IL_001b: box [System.Private.CoreLib]System.Double IL_0020: ldc.r8 6 IL_0029: box [System.Private.CoreLib]System.Double IL_002e: call object Class::Add(object, object) IL_0033: pop IL_0034: ret } // end of method Class::Method 

محملة 5 ، معبأة ، محملة 6 ، معبأة ، تسمى object Add(object, object) .
الخيار الواضح لا يناسبنا.

التجربة الثانية ، "في الجبهة"

حسنًا ، dynamic ليست لنا ، لكن عدد أنواعنا محدود ، وهي معروفة مسبقًا. فلنسلح أنفسنا بمجموعة من الفروع ونكتبها : إذا كان نوعنا هو ، فلنحسب شيئًا ، وإلا - هنا هو الاستثناء.

 public static T Add<T>(T left, T right) where T : unmanaged { if(left is int i32Left && right is int i32Right) { // ??? } // ... throw new NotSupportedException(); } 

ثالثًا ، ها نحن نواجه مشكلة. إذا فهمت الأنواع التي نعمل معها ، فلا يزال بإمكانك تطبيق العملية عليها أيضًا ، ثم يجب تحويل int الشرطي الناتج إلى نوع T غير معروف وهذا ليس بالأمر السهل. لا يتم تجميع return (T)(i32Left + i32Right) ليس هناك ما يضمن أن يكون T int (على الرغم من أننا نعرف أنه). يمكنك محاولة return (T)(object)(i32Left + i32Right) التحويل المزدوج return (T)(object)(i32Left + i32Right) . أولاً ، يتم تعبئة الكمية ، ثم يتم تفريغها في T لن يعمل هذا إلا إذا كانت الأنواع مطابقة قبل التعبئة وبعد التغليف. لا يمكنك حزم int ، لكن تفريغها double ، حتى إذا كان هناك تحويل ضمني int -> double . المشكلة في هذا الكود هي التفرع العملاق ووفرة حزم التفريغ ، حتى if الظروف. هذا الخيار هو أيضا ليست جيدة.

الانعكاس والبيانات الوصفية

حسنا ، العب وهذا يكفي. يعلم الجميع أن هناك عوامل تشغيل في C# يمكن تجاوزها. هناك ، + ، - ، == ، == != وهلم جرا. كل ما نحتاج إلى القيام به هو سحب أسلوب ثابت من النوع T يتوافق مع المشغل ، على سبيل المثال ، الإضافات - هذا كل شيء. حسنا ، نعم ، مرة أخرى بضع حزم ، ولكن لا المتفرعة ولا مشاكل. يمكن تخزين كل شيء في ذاكرة التخزين المؤقت حسب النوع T وبصورة عامة تسريع العملية بكل طريقة ، مما يقلل من عملية رياضية واحدة لاستدعاء طريقة انعكاس واحدة. حسنًا ، شيء مثل هذا:

 public static T Add<T>(T left, T right) where T : unmanaged { // Simple example without cache. var method = typeof(T) .GetMethod(@"op_Addition", new [] {typeof(T), typeof(T)}) ?.CreateDelegate(typeof(Func<T, T, T>)) as Func<T, T, T>; return method?.Invoke(left, right) ?? throw new InvalidOperationException(); } 

لسوء الحظ هذا لا يعمل . والحقيقة هي أن الأنواع الحسابية (ولكن ليس decimal ) لا تملك مثل هذه الطريقة الساكنة. يتم تنفيذ جميع العمليات من خلال عمليات IL ، مثل add . الانعكاس الطبيعي لا يحل مشكلتنا.

System.Linq.Expressions

تم توضيح الحل القائم على Expressions في مدونة John Skeet هنا (بواسطة Marc Gravell).
الفكرة بسيطة جدا. افترض أن لدينا نوع T يدعم العملية + . لنقم بإنشاء تعبير مثل هذا:

 (x, y) => x + y; 

بعد ذلك ، بعد التخزين المؤقت ، سوف نستخدمها. بناء مثل هذا التعبير سهل جدا. نحن بحاجة إلى معلمتين وعملية واحدة. لذلك دعونا نكتبها.

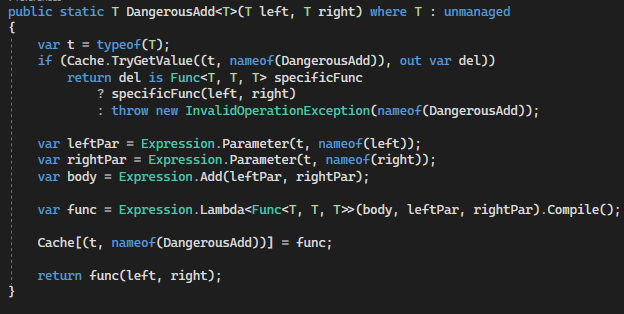
 private static readonly Dictionary<(Type Type, string Op), Delegate> Cache = new Dictionary<(Type Type, string Op), Delegate>(); public static T Add<T>(T left, T right) where T : unmanaged { var t = typeof(T); // If op is cached by type and function name, use cached version if (Cache.TryGetValue((t, nameof(Add)), out var del)) return del is Func<T, T, T> specificFunc ? specificFunc(left, right) : throw new InvalidOperationException(nameof(Add)); var leftPar = Expression.Parameter(t, nameof(left)); var rightPar = Expression.Parameter(t, nameof(right)); var body = Expression.Add(leftPar, rightPar); var func = Expression.Lambda<Func<T, T, T>>(body, leftPar, rightPar).Compile(); Cache[(t, nameof(Add))] = func; return func(left, right); } 

تم نشر معلومات مفيدة حول أشجار التعبير والمندوبين على المحور

من الناحية الفنية ، تسمح لنا التعبيرات بحل جميع مشكلاتنا - أي عملية أساسية يمكن اختزالها إلى استدعاء طريقة عامة. يمكن كتابة أي عملية أكثر تعقيدًا بنفس الطريقة ، باستخدام تعبيرات أكثر تعقيدًا. هذا يكفي تقريبا .

نحن كسر كل القواعد

هل من الممكن تحقيق شيء آخر باستخدام قوة CLR/C# ؟ لنرى ما هي السنة التي يتم فيها إنشاء الكود بواسطة طرق الإضافة لأنواع مختلفة :

 public class Class { public static double Add(double x, double y) => x + y; public static int Add(int x, int y) => x + y; // Decimal only to show difference public static decimal Add(decimal x, decimal y) => x + y; } 

يحتوي رمز IL المطابق على نفس مجموعة التعليمات:

 ldarg.0 ldarg.1 add ret 

هذا هو رمز المرجع ذاته الذي يتم فيه جمع أنواع بدائية حسابية. decimal في هذا المكان يستدعي static decimal decimal.op_Addition(decimal, decimal) . ولكن ماذا لو كتبنا طريقة سيتم تعميمها ، ولكن تحتوي على هذا الرمز بالضبط؟ حسنًا ، جون سكيت يحذر من أن هذا لا يستحق العناء . في حالته ، فهو يأخذ في الاعتبار جميع الأنواع (بما في ذلك decimal ) ، وكذلك nullable الفارغة. سيتطلب ذلك عمليات IL غير تافهة تمامًا وسيؤدي بالضرورة إلى حدوث خطأ. ولكن لا يزال بإمكاننا محاولة تنفيذ العمليات الأساسية.

لدهشتي ، لا يحتوي Visual Studio على قوالب لمشاريع IL وملفات IL . لا يمكنك فقط أخذ جزء من الكود ووصفه في IL وإدراجه في التجميع الخاص بك. بطبيعة الحال ، المصدر المفتوح يأتي لمساعدتنا. يحتوي مشروع ILSupport على قوالب لمشاريع IL ، بالإضافة إلى مجموعة من الإرشادات التي يمكن إضافتها إلى *.csproj لتضمين IL code في المشروع. بالطبع ، من الصعب جدًا وصف كل شيء في IL ، لذلك يستخدم مؤلف المشروع السمة MethodImpl مع علامة ForwardRef . تسمح لك هذه السمة بتعريف الطريقة على أنها extern وليس وصف نص الطريقة. يبدو شيء مثل هذا:

 [MethodImpl(MethodImplOptions.ForwardRef)] public static extern T Add<T>(T left, T right) where T : unmanaged; 

الخطوة التالية هي كتابة تنفيذ الطريقة في ملف *.il برمز IL :

 .method public static hidebysig !!T Add<valuetype .ctor (class [mscorlib]System.ValueType modreq ([mscorlib]System.Runtime.InteropServices.UnmanagedType)) T>(!!T left, !!T right) cil managed { .param type [1] .custom instance void System.Runtime.CompilerServices.IsUnmanagedAttribute::.ctor() = (01 00 00 00 ) ldarg.0 ldarg.1 add ret } 

في أي مكان تشير صراحة إلى النوع !!T ، نقترح CLR لإضافة وسيطين وإرجاع النتيجة. لا توجد اختبارات النوع ، وكل شيء على ضمير المطور. والمثير للدهشة ، أنه يعمل ، وبسرعة نسبيا .

قليلا من المعيار

ربما ، سيتم بناء معيار صريح على بعض التعقيدات المعقدة إلى حد ما ، حيث يتم حساب "وجهاً لوجه" بمقارنة هذه الأساليب الخطيرة. كتبت خوارزمية بسيطة تلخص مربعات الأرقام التي تم حسابها مسبقًا وتخزينها في صفيف double وقسمت المبلغ النهائي على عدد الأرقام. لتنفيذ العملية ، استخدمت عوامل تشغيل C# + و * و / و ، كما يفعل الأشخاص الأصحاء ، وظائف تم إنشاؤها باستخدام Expressions ووظائف IL .

 BenchmarkDotNet=v0.12.0, OS=Windows 10.0.18362 Intel Core i7-2700K CPU 3.50GHz (Sandy Bridge), 1 CPU, 8 logical and 4 physical cores .NET Core SDK=3.1.100 [Host] : .NET Core 3.1.0 (CoreCLR 4.700.19.56402, CoreFX 4.700.19.56404), X64 RyuJIT Job-POXTAH : .NET Core 3.1.0 (CoreCLR 4.700.19.56402, CoreFX 4.700.19.56404), X64 RyuJIT Runtime=.NET Core 3.1 

الكود غير الآمن لدينا هو حوالي 2.5 مرة أبطأ (من حيث عملية واحدة). يمكن أن يعزى ذلك إلى حقيقة أنه في حالة حساب "الجبين" ، يقوم المترجم بتجميع a + b في كود add op ، وفي حالة طريقة غير آمنة ، تسمى وظيفة ثابتة ، والتي تكون بطيئة بشكل طبيعي.

بدلاً من الاستنتاج: عندما يكون true != true

قبل بضعة أيام ، صادفت مثل هذه التغريدة من Jared Parsons:

هناك حالات حيث تتم طباعة ما يلي "false"
منطقي ب = ...
إذا (ب) Console.WriteLine (b.IsTrue ()) ؛

كان هذا هو الرد على هذا الإدخال ، والذي يعرض رمز التحقق bool لـ true ، والذي يبدو كالتالي:

 public static bool IsTrue(this bool b) { if (b == true) return true; else if (b == false) return false; else return !true && !false; } 

الشيكات تبدو زائدة عن الحاجة ، أليس كذلك؟ يقدم Jared مثالاً معارضًا يوضح بعض ميزات السلوك bool . الفكرة هي أن bool byte ( sizeof(bool) == 1 ) ، في حين أن التطابقات false 0 والمطابقة true 1 . طالما أنك لا تتأرجح المؤشرات ، يتصرف bool بشكل لا لبس فيه ويمكن التنبؤ به. ومع ذلك ، كما أظهر Jared ، يمكنك إنشاء bool باستخدام الرقم 2 كقيمة أولية ، وسيفشل جزء من عمليات التحقق بشكل صحيح:

 bool b = false; byte* ptr = (byte*)&b; *ptr = 2; 

يمكننا تحقيق تأثير مماثل باستخدام عملياتنا الرياضية غير الآمنة (هذا لا يعمل مع Expressions ):

 var fakeTrue = Subtract<bool>(false, true); var val = *(byte*)&fakeTrue; if(fakeTrue) Assert.AreNotEqual(fakeTrue, true); else Assert.Fail("Clause not entered."); 

نعم ، نعم ، نحن نتفحص داخل الفرع true ما إذا كانت الحالة true ، ونتوقع أن تكون غير true في الواقع. لماذا هذا هكذا؟ إذا قمت بطرح من 0 ( =false ) 1 ( =true ) بدون شيكات ، فإن byte يساوي 255 . بطبيعة الحال ، 255 ( fakeTrue لدينا) ليس 1 ( true حقيقي) ، لذلك يتم تنفيذ التأكيد. المتفرعة تعمل بشكل مختلف.

if حدوث انقلاب: يتم إدخال فرع مشروط ؛ إذا كانت الحالة خاطئة ، يحدث الانتقال إلى النقطة بعد نهاية كتلة if . يتم التحقق من الصحة بواسطة عبارة brfalse / brfalse_S . يقارن القيمة الأخيرة على المكدس مع صفر . إذا كانت القيمة صفرية ، فعندئذ تكون false ، فإننا نخطو كتلة if . في حالتنا ، فإن fakeTrue لا تساوي الصفر ، وبالتالي فإن عملية الفحص تستمر والتنفيذ داخل كتلة if ، حيث نقارن fakeBool بالقيمة الحقيقية والحصول على نتيجة سلبية.

UPD01:
بعد المناقشة في التعليقات مع shai_hulud و blowin ، أضفت طريقة أخرى للمعايير التي تنفذ فرعا مثل if(typeof(T) == typeof(int)) return (T)(object)((int)(object)left + (int)(object)right); . على الرغم من حقيقة أنه يجب على JIT تحسين عمليات الفحص ، على الأقل عندما تكون T struct ، فإن هذه الأساليب لا تزال تعمل بترتيب أبطأ. ليس من الواضح ما إذا كانت التحويلات T -> int -> T أمثل أم لا ، أو ما إذا كان يتم استخدام الملاكمة / unboxing. MethodImpl تتأثر نتائج المؤشر بشكل كبير MethodImpl .

UPD02:
وأظهر xXxVano في التعليقات مثالًا على استخدام المتفرعة حسب النوع Unsafe.As<TFrom, TTo>() T <--> نوعًا محددًا باستخدام Unsafe.As<TFrom, TTo>() . عن طريق القياس مع التفرع المعتاد والعرف من خلال object ، كتبت ثلاث عمليات (الجمع والضرب والقسمة) مع المتفرعة لجميع أنواع الحسابات ، وبعد ذلك أضفت معيارًا آخر ( UnsafeBranchSum ). على الرغم من حقيقة أن جميع الطرق (باستثناء التعبيرات) تولد رمز asm متطابقًا تقريبًا (بقدر ما تسمح لي معرفتي المحدودة بالتجميع بالحكم) ، لسبب غير معروف ، فإن كلا الطريقتين DirectSum بطيئة جدًا مقارنة بكل من الجمع المباشر ( DirectSum ) و باستخدام الوراثة و IL رمز. ليس لدي أي تفسير لهذا التأثير ، حقيقة أن الوقت الذي تستغرقه الزيادات يتناسب مع N يشير إلى وجود نوع من الحمل الثابت لكل عملية ، على الرغم من سحر JIT . هذا الحمل مفقود من إصدار IL الأساليب. , IL - , / / , 100% ( , ).
, , - .