مساء الخير
سأحاول في هذه المقالة إلقاء نظرة جديدة على الخوارزمية لإيجاد حل عام لنظام المعادلات الخطية.
المهمة التي سنفعلها سليمة مثل هذا.
ابحث عن حل عام لنظام المعادلات التالي
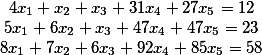
يتم حل هذه المشكلة عن طريق تقليل النظام الأولي إلى شكل مثلث وفقًا لطريقة Gauss. ثم ، باختيار المتغيرات المجانية ، يتم حساب الحل العام.
أريد أن أوضح كيف يمكن للمرء أن يحل مثل هذه الأنظمة بطريقة أخرى. بقدر ما هو معروف وتطبيقها في مكان آخر ، لم أستطع معرفة ذلك. في جميع المواد العامة / الشعبية ، يتم استخدام طريقة غاوس.
يجب أن أقول على الفور أن الحل ليس بالتأكيد هو الأمثل (من حيث السرعة) ، لأنه عند حساب منتج متجه ، من الضروري حساب محدد المصفوفة ، وهذا هو حساب المصفوفة الثلاثية بطريقة أو بأخرى.
لكن الحل جميل وواضح ، إلى جانب ذلك ، من السهل أن نرى المعيار الذي لا يوجد فيه أي حلول للنظام.
ما هو جوهر هذه التقنية؟
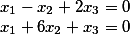
حل هذا النظام كمنتج من متجهين نحصل عليه
i%20+%20(%201%20)j%20+%20(%207%20)k)
لذلك ، جذور النظام متساوية
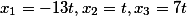
بالنسبة لأولئك الذين لا يؤمنون ، يتم التحقق من ذلك بسهولة عن طريق الاستبدال.
نحن نستخدم هذه التقنية وننظر في كيفية حل هذه الأنظمة باستخدام منتجات مكافحة ناقلات الأمراض.
لذلك لدينا نظام المصدر
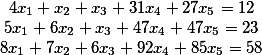
نقل الشروط الحرة إلى الجانب الأيسر
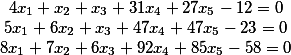
لدينا 6 أعمدة.
في هذه المرحلة ، لن نقدم كيانات جديدة ولن نستخدم مفاهيم ترتيب المصفوفات في عملنا. (من فضلك عاملني بشكل متقن)
نرى فقط أن هناك 3 معادلات ، و 5 متغيرات. لذلك ، سوف يستخدم الحل العام 5-3 = 2 متغيرات مستقلة.
في نفس الخطوة ، يمكننا تحديد أي من المتغيرات ستكون حرة. نحن نأخذ متغيرين سيكونان على يمين الجميع ونطلق سراحهما.
ملاحظة: بالنسبة للمعادلات الأخرى ، لا يتضح دائمًا أنه من الضروري أخذ آخر معاملات صحيحة فقط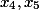
والآن في ثلاث خطوات نحدد الحل الأساسي للنظام الأصلي
الخطوة 1. هنا العمود الأخير هو أعضاء النظام المجانيين.
i%20+%20(%20-162%20)j%20+%20(%20-486%20)k%20+%20(%20-81%20)l)
الخطوة 2. هنا العمود الأخير هو معاملات للمتغير
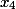
i%20+%20(%20162%20)j%20+%20(%20405%20)k%20+%20(%20-81%20)l)
الخطوة 3. هنا العمود الأخير هو معاملات للمتغير
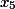
i%20+%20(%20243%20)j%20+%20(%20324%20)k%20+%20(%20-81%20)l)
ليست هناك حاجة لمعرفة التفاصيل التي نحصل عليها من البيانات. أعتقد أن هذا واضح للقراء. (كل من حل نظام المعادلات باستخدام طريقة Cramer سيجد ميزات مشتركة)
ما هو أكثر إثارة للاهتمام هو ما سنفعله مع هذه "المتجهات".
قسّمهم على -81
نحصل على المتجهات الثلاثة التالية
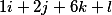
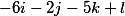
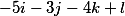
رتبهم رأسياً وبالتالي يتخذ القرار الأساسي الشكل
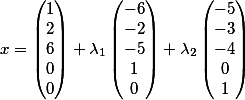
عظيم! أليس كذلك ...
بالنسبة لمعيار القابلية للحل لنظام معادلات معين ، في معظم الحالات يتم استخدام قاعدة Kronecker-Copelli ، وهنا يتم تحليل نتيجة منتج المتجه ببساطة.
إذا كان المتجه الناتج لديه النموذج
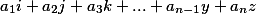
حيث 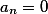 ، ومن بين كل ما تبقى هناك واحد على الأقل غير صفري ، ثم لا يوجد مثل هذا النظام من الحلولإذا كان المتجه الناتج يحتوي على جميع معاملات الصفر ، فإن هذا يشير إلى أن أحد المعادلات على الأقل يمثل خطيًا للآخر ، و / أو أن أحد المتغيرات يتناسب مع الآخر.
، ومن بين كل ما تبقى هناك واحد على الأقل غير صفري ، ثم لا يوجد مثل هذا النظام من الحلولإذا كان المتجه الناتج يحتوي على جميع معاملات الصفر ، فإن هذا يشير إلى أن أحد المعادلات على الأقل يمثل خطيًا للآخر ، و / أو أن أحد المتغيرات يتناسب مع الآخر.هذا المقال هو الأول ، وأود أن أسمع التعليقات والنقد والرغبات في خطابي.
تم
إنشاء الخوارزمية والحاسبة
مرة أخرى في يناير 2019 ، واليوم فقط قررت نشر معلومات عن حبري.
إذا وافقت في فريقك / مجتمعك ، فسيكون الموضوع التالي
- كيفية إيجاد حل عام لنظام معادلات ديوفانتاين.