
تعد أجهزة الكمبيوتر الكمومية والحوسبة الكمومية كلمة طنانة جديدة تمت إضافتها إلى مساحة المعلومات الخاصة بنا جنبًا إلى جنب مع الذكاء الاصطناعي والتعلم الآلي ومصطلحات التكنولوجيا المتقدمة الأخرى. في الوقت نفسه ، لم أتمكن من العثور على مواد على الإنترنت تضع في ذهني لغزًا يسمى "كيف تعمل أجهزة الكمبيوتر الكمومية" . نعم ، هناك العديد من الأعمال الممتازة ، بما في ذلك على Habré (انظر قائمة الموارد ) ، التعليقات التي ، كما يحدث عادة ، أكثر إفادة ومفيدة ، ولكن الصورة في الرأس ، كما يقولون ، لم تضيف ما يصل.
ومؤخراً ، جاء إليّ زملائي وسألوا "هل تفهم كيف يعمل الكمبيوتر الكمومي؟ هل يمكن أن تخبرنا؟ "ثم أدركت أن مشكلة طي صورة كاملة في رأسي ليست مشكلتي فقط.
نتيجة لذلك ، جرت محاولة لتجميع المعلومات حول أجهزة الكمبيوتر الكمومية في مخطط منطقي ثابت ، وفي المستوى الأساسي ، وبدون الانغماس العميق في الرياضيات وبنية العالم الكمومي ، تم شرح ماهية الكمبيوتر الكمومي ، وما هي المبادئ التي يعمل عليها ، وأيضًا المشكلات التي واجهته. العلماء في إنشائها وتشغيلها.
جدول المحتويات
تنصل
(للمحتويات)
المؤلف ليس متخصصًا في الحوسبة الكمومية ، والجمهور المستهدف من المقال هو نفس خبراء تكنولوجيا المعلومات ، وليسوا متخصصي الكم ، الذين يريدون أيضًا أن يضعوا في رؤوسهم صورة تسمى "كيف تعمل أجهزة الكمبيوتر الكمومية". ولهذا السبب ، يتم تبسيط العديد من المفاهيم في المقالة بشكل متعمد لفهم أفضل لتقنيات الكم على المستوى "الأساسي" ، ولكن دون تبسيط كبير مع فقد محتوى المعلومات وكفايتها .
في بعض الأماكن ، تستخدم المقالة مواد من مصادر أخرى ، يتم تقديم قائمة بها في نهاية المقالة . حيثما كان ذلك ممكنا ، يتم إدراج الروابط المباشرة والمراجع إلى النص الأصلي أو الجدول أو الصورة. إذا نسيت شيئا ما (أو شخص ما) ، فاكتب - سأقوم بتصحيحه.
مقدمة
(للمحتويات)
في هذا الفصل ، سننظر بإيجاز في كيفية بدء عصر الكم ، والذي كان الدافع وراء فكرة وجود كمبيوتر كمومي ، والذي (أي البلدان والشركات) هو اللاعب الرئيسي في هذا المقاصة ، وسنتحدث بإيجاز عن الاتجاهات الرئيسية لتطوير الحوسبة الكمومية.
كيف بدأ كل شيء
(للمحتويات)

تعتبر النقطة المرجعية للعصر الكمومي هي عام 1900 ، عندما طرح M. Planck أولاً فرضية أن الطاقة تنبعث وتستوعب ليس بشكل مستمر ، ولكن في كمية منفصلة (أجزاء). تم اختيار الفكرة وتطويرها من قبل العديد من العلماء البارزين في ذلك الوقت - بوهر ، آينشتاين ، هايزنبرغ ، شرودنجر ، مما أدى في النهاية إلى إنشاء وتطوير علم مثل فيزياء الكم . هناك الكثير من المواد الجيدة حول تطور فيزياء الكم كعلم على شبكة الإنترنت ، في هذه المقالة لن نتحدث عن ذلك بالتفصيل ، ولكن كان من الضروري الإشارة إلى التاريخ الذي دخلنا فيه إلى عصر الكم الجديد.
جلبت فيزياء الكم إلى حياتنا العادية العديد من الاختراعات والتقنيات ، والتي بدونها يصعب الآن تخيل العالم من حولنا. على سبيل المثال ، ليزر ، يُستخدم الآن في كل مكان ، من الأجهزة المنزلية (مستويات الليزر ، إلخ) إلى أنظمة التكنولوجيا الفائقة (ليزر تصحيح الرؤية ، مرحباً بالماكلون ). سيكون من المنطقي أن نفترض أن شخصًا ما عاجلاً أم آجلاً سوف يطرح فكرة لماذا لا نستخدم الأنظمة الكمية لإجراء العمليات الحسابية. وهذا ما حدث في عام 1980.
تشير ويكيبيديا إلى أن العالم يوري مانين كان أول من عبر عن فكرة الحوسبة الكمومية في عام 1980. لكنهم بدأوا بالفعل الحديث عن ذلك فقط في عام 1981 ، عندما أشار R. Feynman المشهور ، في تقرير في المؤتمر الأول حول الفيزياء الحاسوبية الذي عقد في معهد ماساتشوستس للتكنولوجيا ، إلى أنه من المستحيل وضع نموذج لتطور نظام الكم على جهاز كمبيوتر كلاسيكي بطريقة فعالة. اقترح نموذجًا أوليًا للكمبيوتر الكمومي الذي سيكون قادرًا على إجراء مثل هذه المحاكاة.
يوجد مثل هذا العمل على الويب حيث يتم اعتبار التسلسل الزمني لتطوير الحوسبة الكمومية أكثر أكاديمية وتفصيلية ، لكننا سننتقل بإيجاز:
المعالم البارزة في تاريخ الحواسيب الكمومية:
كما ترون ، مرت 17 عامًا (من 1981 إلى 1998) من لحظة الفكرة إلى أول تطبيق لها في جهاز كمبيوتر يحتوي على 2 بت ، و 21 عامًا (من 1998 إلى 2019) حتى اللحظة التي زاد فيها عدد البتات إلى 53. استغرق الأمر 11 عامًا (من 2001 إلى 2012) لتحسين نتيجة خوارزمية Shore (سنتطرق إليها أكثر قليلاً) من الرقم 15 إلى 21. أيضًا ، قبل ثلاثة أعوام فقط أدركنا ما كان يتحدث عنه فينمان ، و تعلم محاكاة أبسط النظم المادية.
تطوير الحوسبة الكمومية بطيء. يواجه العلماء والمهندسون مهام معقدة للغاية ، والحالات الكمومية قصيرة الأجل وهشة للغاية ، ومن أجل إبقائها طويلة بما يكفي لإجراء العمليات الحسابية ، يتعين على المرء بناء التابوت لعشرات الملايين من الدولارات ، حيث يتم الحفاظ على درجة الحرارة أعلى من الصفر المطلق ، والتي تكون محمية من التأثيرات الخارجية. كذلك سنتحدث عن هذه المهام والمشاكل بمزيد من التفصيل.
كبار اللاعبين
(للمحتويات)

شرائح هذا القسم مأخوذة من مقالة Quantum Computer: A Big Boost Game. محاضرة في ياندكس ، من باحث في المركز الكمي الروسي الكم أليكسي فيدوروف. سأسمح لنفسي باقتباسات مباشرة:
تعمل جميع البلدان الناجحة تقنياً حاليًا بنشاط في تطوير التقنيات الكمومية. يتم استثمار مبلغ كبير من المال في هذه الدراسات ، ويتم إنشاء برامج خاصة لدعم تقنيات الكم.

سباق الكم لا يشمل فقط الدول ، ولكن يشمل أيضًا الشركات الخاصة. في المجموع ، استثمرت Google و IBM و Intel و Microsoft حوالي 0.5 مليار دولار في تطوير أجهزة الكمبيوتر الكمومية في السنوات الأخيرة ، وأنشأت مختبرات ومراكز أبحاث كبيرة.
هناك العديد من المقالات حول Habré وعلى الويب ، على سبيل المثال ، هنا ، هنا وهنا ، حيث يتم النظر في الوضع الحالي مع تطور تقنيات الكم في بلدان مختلفة بمزيد من التفصيل. بالنسبة لنا الآن ، الشيء الرئيسي هو أن جميع الدول واللاعبين الرائدين من الناحية التكنولوجية يستثمرون مبالغ ضخمة من المال في البحث في هذا الاتجاه ، مما يعطي الأمل في الخروج من المأزق التكنولوجي الحالي.
اتجاهات التنمية
(للمحتويات)

في الوقت الحالي (قد أكون مخطئًا وصحيحًا) تتركز الجهود الرئيسية (ونتائج أكثر أو أقل أهمية) لجميع اللاعبين الرئيسيين في اتجاهين:
- أجهزة الكمبيوتر الكمومية المتخصصة التي تهدف إلى حل مشكلة معينة محددة ، على سبيل المثال ، مشاكل التحسين. مثال على أحد المنتجات هو أجهزة الكمبيوتر الكمومية D-Wave.
- أجهزة الكمبيوتر الكمومية الشاملة - والتي هي قادرة على تنفيذ خوارزميات الكم التعسفي (شور ، غروفر ، وما إلى ذلك). تطبيقات من IBM و Google.
متجهات تطور أخرى تعطينا فيزياء الكم ، مثل:
بالتأكيد أيضًا في قائمة مجالات البحث ، لكن يبدو أن هناك نوعًا من النتائج المهمة أو الأكثر أهمية في الوقت الحالي.
بالإضافة إلى ذلك ، يمكنك قراءة خارطة الطريق لتطوير تقنيات الكم ، حسنا ، جوجل " تطوير تقنيات الكم " ، على سبيل المثال ، هنا ، هنا وهنا .
الأساسيات. كائن الكم والأنظمة الكمومية
(للمحتويات)

الشيء الأكثر أهمية لفهم من هذا القسم هو ذلك
يستخدم الكمبيوتر الكمومي (على عكس الكمبيوتر التقليدي) الكائنات الكمومية كموجهات نقل معلومات ، ويجب توصيل الكائنات الكمومية بنظام كمومي لإجراء العمليات الحسابية.
ما هو كائن الكم؟
الكائن الكمومي هو كائن من العالم المصغر (عالم الكم) الذي يعرض خصائص الكم:
- لديه دولة معينة مع مستويين الحدود
- في تراكب حالته حتى لحظة القياس
- متشابك مع كائنات أخرى لإنشاء أنظمة الكم
- يقوم بنظرية حظر الاستنساخ (لا يمكنك نسخ حالة الكائن)
دعنا نحلل كل خاصية بمزيد من التفاصيل:
لديه حالة معينة مع مستويين حد (الحالة النهائية)
مثال كلاسيكي من العالم الحقيقي هو عملة معدنية. لديها حالة من "الجانب" ، والتي تأخذ مستويين من الحدود - "النسر" و "ذيول".
في تراكب حالته حتى لحظة القياس
قذف قطعة معدنية ، يطير ويدور. أثناء الدوران ، من المستحيل تحديد أي من مستويات الحدود تقع حالتها "الجانبية". ولكن إذا صفقنا ونظرنا إلى النتيجة ، فإن تراكب الدول ينهار على الفور إلى واحد من الحدود - "الرؤوس" و "ذيول". يعتبر انتزاع عملة معدنية في حالتنا بُعدًا.
متشابك مع كائنات أخرى لإنشاء أنظمة الكم
هذا صعب باستخدام عملة معدنية ، لكننا سنحاول. تخيل أننا ألقينا ثلاث عملات معدنية بحيث تدور حول التشبث ببعضها البعض ، مثل خلط العملات. في كل لحظة من الزمن ، ليس كل واحد منهم فقط في حالة تراكب للولايات ، ولكن هذه الدول تؤثر بعضها على بعض (تصطدم العملات المعدنية).
يقوم بنظرية حظر الاستنساخ (لا يمكنك نسخ حالة الكائن)
بينما تطير العملات المعدنية وتدور ، لا يمكننا بأي حال إنشاء نسخة من حالة الدوران لأي من العملات المعدنية المنفصلة عن النظام. يعيش النظام في حد ذاته وهو غيور جدًا على إعطاء أي معلومات.
كلمتين حول مفهوم "التراكب" ذاته ، في جميع المقالات تقريبًا ، يتم شرح التراكب على أنه "موجود في جميع الولايات في نفس الوقت" ، وهو أمر صحيح بالطبع ، ولكنه في بعض الأحيان مربك للغاية. يمكن أيضًا اعتبار تراكب الحالات كحقيقة أنه في كل لحظة من الزمن ، يكون للجسم الكمومي احتمالات معينة للانهيار في كل من مستوياته الحدودية ، وفي المجموع تساوي هذه الاحتمالات بشكل طبيعي 1 . علاوة على ذلك ، عند النظر في qubit ، سنناقش هذا بمزيد من التفصيل.
بالنسبة للعملات المعدنية ، يمكن تخيل ذلك بصريًا - اعتمادًا على السرعة الأولية ، وزاوية إرم ، وحالة البيئة التي تطير فيها العملة المعدنية ، في كل لحظة من الأوقات ، يختلف احتمال الحصول على "نسر" أو "ذيول". وكما ذُكر سابقًا ، يمكن تخيل حالة هذه العملة المتطايرة على أنها "في جميع حالاتها الحدودية في نفس الوقت ، ولكن مع احتمال مختلف لتنفيذها".
يمكن استخدام أي كائن يتم استيفاء الخصائص المذكورة أعلاه والذي يمكننا إنشاؤه وإدارته كوسيط تخزين في كمبيوتر الكم.
أبعد من ذلك بقليل ، سنتحدث عن الوضع الحالي مع التنفيذ المادي للبتات ككائنات كمومية ، وما الذي يستخدمه العلماء الآن بهذه الصفة.
لذلك ، تقول الخاصية الثالثة أن الكائنات الكمومية يمكن أن تتشابك لإنشاء أنظمة كمومية. ما هو نظام الكم؟
نظام الكم هو نظام من الكائنات الكمومية متشابكة مع الخصائص التالية:
- نظام الكم هو في تراكب جميع الحالات المحتملة للأشياء التي يتكون منها
- من المستحيل معرفة حالة النظام حتى لحظة القياس
- في وقت القياس ، يقوم النظام بتنفيذ أحد المتغيرات المحتملة لحالات حدوده
(والتقدم قليلاً)
النتيجة الطبيعية لبرامج الكم :
- يحتوي البرنامج الكمي على حالة معينة من النظام عند الإدخال ، تراكب في الداخل ، تراكب في الإخراج
- عند إخراج البرنامج بعد القياس ، لدينا تطبيق احتمالي لأحد الحالات النهائية المحتملة للنظام (بالإضافة إلى الأخطاء المحتملة)
- أي برنامج كمي له بنية مدخنة (المدخلات -> الإخراج. لا توجد دورات ، لا يمكنك رؤية حالة النظام في منتصف العملية.)
مقارنة بين الكمبيوتر الكم والتقليدية
(للمحتويات)

لنقم الآن بمقارنة الكمبيوتر التقليدي بالكمبيوتر الكمومي.
مستوى المنطق

على جهاز كمبيوتر عادي ، وهذا قليلا. معروفة بعض الشيء حتمية من خلال وعبر. يمكن أن تأخذ القيم إما 0 أو 1. تتكيف بشكل جيد مع دور وحدة منطقية لجهاز كمبيوتر عادي ، ولكنها غير مناسبة تمامًا لوصف حالة كائن الكم ، والتي ، كما قلنا بالفعل ، موجودة في البرية مع افتراض حالات الحدود .
لهذا ، اخترع qubit . في حالاته الحدودية ، فإنه يدرك الحالات | 0> و | 1> تشبه 0 و 1 ، وفي التراكب يمثل توزيع احتمالي على حالاته الحدودية |0> و |1> :
a|0> + b|1>, , a^2+b^2=1
في هذه الحالة ، تمثل a و b سعة الاحتمالات ، وتمثل المربعات في الوحدات الخاصة بها الاحتمالات في الواقع للحصول على مثل هذه القيم للحالات الحدودية على وجه التحديد |0> و |1>, حالة انهيار qubit بواسطة القياس في الوقت الحالي.
المستوى المادي
في المستوى التكنولوجي الحالي للتنمية ، يعد التنفيذ الفعلي للبتات لجهاز الكمبيوتر العادي بمثابة ترانزستور أشباه الموصلات ، بالنسبة لكمية ، كما قلنا ، أي كائن كمي . في القسم التالي ، سنتحدث عن ما يتم استخدامه حاليًا كحاملات مادية للبتات.
متوسطة التخزين
بالنسبة إلى جهاز كمبيوتر عادي ، يكون هذا تيارًا كهربائيًا - مستويات الجهد ، وجود أو عدم وجود تيار ، وما إلى ذلك ، بالنسبة للكم الكمومي - حالة الجسم الكمومي (اتجاه الاستقطاب ، الدوران ، إلخ) ، والتي قد تكون في حالة تراكب.
العمليات
لتنفيذ دوائر منطقية على جهاز كمبيوتر عادي ، نستخدم جميعنا عمليات منطقية معروفة ؛ وبالنسبة للعمليات على الكبت ، كان علينا التوصل إلى نظام مختلف تمامًا للعمليات يسمى البوابات الكمومية . البوابات أحادية البايت واثنين من البايتات ، اعتمادًا على عدد البتات التي تم تحويلها.
أمثلة على البوابات الكمومية:
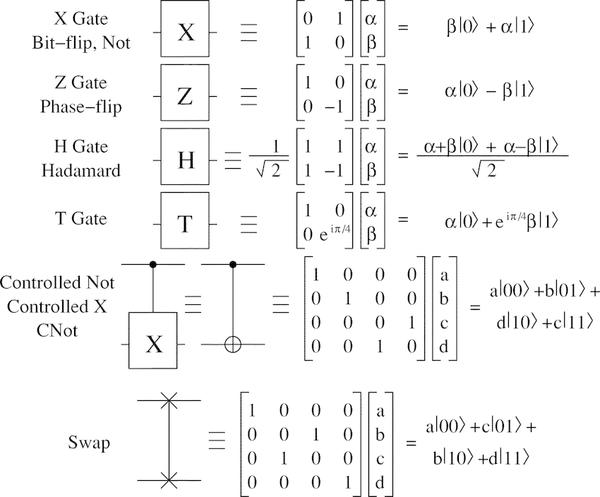
هناك مفهوم مجموعة عالمية من البوابات ، والتي هي كافية لإجراء أي حساب الكم. على سبيل المثال ، تشتمل المجموعة الشاملة على صمام Hadamard وصمام إزاحة الطور وصمام CNOT وصمام π⁄8. من خلال مساعدتهم ، يمكنك إجراء أي حساب الكم على مجموعة عشوائية من البتات.
في هذه المقالة ، لن نتناول بالتفصيل نظام البوابات الكمومية ؛ بمزيد من التفصيل عنهم ، يمكن قراءة العمليات المنطقية على البتات ، على سبيل المثال ، هنا . الشيء الرئيسي الذي يجب تذكره:
- تتطلب العمليات على الكائنات الكمومية إنشاء عوامل تشغيل منطقية جديدة (بوابات كمومية)
- الصمامات الكمومية أحادية البايت واثنين من الكوابت
- هناك مجموعات عالمية من البوابات التي يمكنك إجراء أي حساب الكم
العلاقة المتبادلة
لا يعد لنا أي ترانزستور عديم الفائدة تمامًا ، ولإجراء عمليات حسابية نحتاج إلى توصيل العديد من الترانزستورات ببعضها البعض ، أي إنشاء رقاقة أشباه الموصلات من ملايين الترانزستورات ، التي نبني عليها بالفعل دوائر منطقية و ALU ، وفي النهاية نحصل على معالج حديث في شكله الكلاسيكي.
واحد بايت هو أيضا عديمة الفائدة تماما بالنسبة لنا (حسنا ، إذا فقط من الناحية الأكاديمية) ،
لإجراء عمليات حسابية ، نحتاج إلى نظام من وحدات البت (الأجسام الكمومية)
والتي ، كما قلنا بالفعل ، يتم إنشاؤها عن طريق تشابك معاهدات الاستثمار الثنائية فيما بينها بحيث تحدث التغييرات في ولاياتها في حفلة موسيقية.
خوارزميات
الخوارزميات القياسية التي تراكمت لدى البشرية حتى اللحظة الحالية غير مناسبة تمامًا للتنفيذ على كمبيوتر الكم. نعم ، بشكل عام ، وليس هناك حاجة. تتطلب أجهزة الكمبيوتر الكمومية المستندة إلى منطق البوابة عبر وحدات البت إنشاء خوارزميات مختلفة تمامًا ، خوارزميات الكم. من خوارزميات الكم الأكثر شهرة ، يمكن تمييز ثلاث:
مبدأ
والفرق الأكثر أهمية هو مبدأ العمل. بالنسبة إلى الكمبيوتر القياسي ، يعد هذا مبدأ رقميًا ومحددًا تمامًا ، استنادًا إلى حقيقة أننا إذا وضعنا بعض الحالة الأولية للنظام وتمريره من خلال خوارزمية معينة ، فستكون نتيجة الحسابات هي نفسها بغض النظر عن عدد المرات التي نجري فيها هذا الحساب. في الواقع ، هذا السلوك هو بالضبط ما نتوقعه من الكمبيوتر.
يعمل الكمبيوتر الكمومي على مبدأ احتمالي تمثيلي . نتيجة لخوارزمية معينة في حالة أولية معينة هي عينة من توزيع الاحتمالات للتطبيقات النهائية للخوارزمية بالإضافة إلى الأخطاء المحتملة.
ترجع هذه الطبيعة الاحتمالية للحوسبة الكمومية إلى الجوهر الاحتمالي للغاية للعالم الكمومي. قال آينشتاين القديم: "الله لا يلعب النرد مع الكون " ، لكن كل التجارب والملاحظات حتى الآن (في النموذج العلمي الحالي) تؤكد عكس ذلك.
تطبيقات البدنية لل qubits
(للمحتويات)

كما قلنا بالفعل ، يمكن تمثيل الكوبيت بواسطة كائن كمي ، أي كائن مادي يقوم بتنفيذ الخصائص الكمومية الموصوفة أعلاه. وهذا يعني ، تقريبًا ، أن أي كائن مادي يوجد به حالتان وتكون هاتان الولايتان في حالة تراكب يمكن استخدامه لإنشاء كمبيوتر كمّي.
"إذا استطعنا وضع ذرة على مستويين مختلفين والتحكم فيها ، فهناك غبي. إذا استطعنا القيام بذلك مع أيون ، غبي. إنه نفس الشيء مع التيار. إذا قمنا بتشغيله في اتجاه عقارب الساعة وعكس اتجاه عقارب الساعة في نفس الوقت ، فهناك غبي. " (C)
يوجد تعليق رائع على المقالة التي يتم فيها النظر في مجموعة متنوعة من الإنجازات المادية الحالية لـ qubit بمزيد من التفصيل ، لكننا نورد أكثرها شهرة وشائعة:
من بين كل هذا التنوع ، فإن الطريقة الأولى لإنتاج البتات على أساس الموصلات الفائقة هي الطريقة الأكثر تفصيلاً. تستخدمه Google و IBM و Intel واللاعبون الرئيسيون الآخرون في بناء أنظمتها.
حسنًا ، اقرأ أيضًا استعراض الإنجازات الجسدية المحتملة للبتات من أندرو دالي ، 2014 .
الأساسيات. مبدأ تشغيل الكمبيوتر الكم
(للمحتويات)

المواد لهذا القسم (المهمة والصور) مأخوذة من مقالة "فقط حول المجمع. كيف يعمل الكمبيوتر الكمومي . "
لذلك ، دعونا نتخيل أن لدينا المهمة التالية:
هناك مجموعة من ثلاثة أشخاص: (أ) ندري ، (ب) أولوديا و (C) بدعة . هناك نوعان من سيارات الأجرة (0 و 1) .
ومن المعروف أيضًا أن:
- (أ) ندري ، (ب) أولوديا - الأصدقاء
- (أ) ندري ، (ج) بدعة - أعداء
- (ب) olodya و (C) بدعة - أعداء
المهمة: ضع الأشخاص بسيارات الأجرة حتى يتمكن Max (الأصدقاء) و Min (الأعداء)
النتيجة: L = (عدد الأصدقاء) - (عدد الأعداء) لكل خيار إقامة
هام: افترض أنه لا يوجد منهج إرشادي ، لا يوجد حل مثالي. في هذه الحالة ، يتم حل المشكلة فقط من خلال البحث الشامل للخيارات.
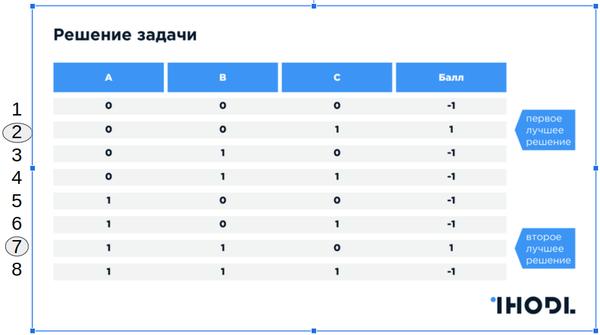
الحل على الكمبيوتر العادي
كيفية حل هذه المشكلة على جهاز كمبيوتر (أو مجموعة) عادي (فائق) - من الواضح أننا نحتاج إلى فرز جميع الخيارات الممكنة في حلقة . إذا كان لدينا نظام متعدد المعالجات ، فيمكننا عندئذ موازاة حساب الحلول على عدة معالجات ثم نجمع النتائج.
لدينا خياران ممكنان للإقامة (التاكسي 0 وسيارة الأجرة 1) و 3 أشخاص. مساحة الحلول هي 2 ^ 3 = 8 . يمكنك الذهاب من خلال 8 خيارات حتى على آلة حاسبة ، هذه ليست مشكلة. والآن سوف نعقد المهمة - لدينا 20 شخصًا وحافلتين ، مساحة الحل هي 2 ^ 20 = 1،048،576 . لا شيء معقد للغاية. دعنا نزيد عدد الأشخاص بمقدار 2.5 مرة - خذ 50 شخصًا وقطارين ، مساحة القرار الآن 2 ^ 50 = 1.12 x 10 ^ 15 . الكمبيوتر العادي (الفائق) بدأ بالفعل في مواجهة مشكلات خطيرة. سنزيد عدد الأشخاص مرتين ، وسيمنحنا 100 شخص 1.2 × 10 ^ 30 خيارًا ممكنًا.
كل شيء ، في وقت معقول ، لا يمكن حساب هذه المهمة.
نحن نربط العملاق
يعد أقوى جهاز كمبيوتر حاليًا هو الرقم 1 في جهاز Top500 ، وهو جهاز القمة بسعة 122 Pflops . لنفترض أنه لحساب خيار واحد ، 100 عملية كافية بالنسبة لنا ، ثم لحل المشكلة بالنسبة إلى 100 شخص نحتاج:
(1.2 × 10 ^ 30 100) / 122 × 10 ^ 15 / (60 60 24 365) = 3 × 10 ^ 37 سنة.
كما نرى ، مع زيادة بُعد البيانات المصدر ، يزداد مساحة الحلول وفقًا لقانون الطاقة ، وفي الحالة العامة بالنسبة إلى N bits لدينا 2 ^ N من الحلول الممكنة التي ، مع وجود عدد صغير نسبيًا (100) ، توفر لنا مساحة غير قابلة للقراءة (على المستوى التكنولوجي الحالي) الحلول.
هل هناك أي بدائل؟ كما كنت قد خمنت ، نعم ، هناك.
ولكن قبل أن ننتقل إلى كيف ولماذا تستطيع أجهزة الكمبيوتر الكمومية حل هذه المشاكل بفعالية ، دعنا نتذكر قليلاً حول ماهية توزيع الاحتمالات . لا تشعر بالقلق ، مقالة المراجعة ، لن يكون هناك رياضيات صعبة هنا ، سنحصل على مثال كلاسيكي مع حقيبة وكرات.
قليلا جدا من التوافقية ، ونظرية الاحتمال وتجربة غريبة
خذ حقيبة وضعي فيها 1000 كرة بيضاء و 1000 كرة سوداء . سنجري تجربة - نخرج الكرة ونكتب اللون ونعيد الكرة إلى الكيس ونخلط الكرات في الكيس.
أجرينا التجربة 10 مرات ، وانسحبت 10 كرات سوداء . ربما؟ هو عليه. هل تعطينا هذه العينة مفهومًا معقولًا للتوزيع الحقيقي في الكيس؟ من الواضح لا. ما عليك القيام به هو الصحيح ، كرر التجربة مليون مرة وحساب وتيرة سقوط الكرات بالأبيض والأسود. نحصل ، على سبيل المثال ، 49.95٪ أسود و 50.05٪ أبيض . في هذه الحالة ، تكون بنية التوزيع التي نتخذ منها عينة أكثر وضوحًا بالفعل (نأخذ كرة واحدة).
الشيء الرئيسي الذي تحتاج إلى فهمه هو أن التجربة بحد ذاتها احتمالية بطبيعتها ، مع عينة واحدة (كرة) لا نتعرف على بنية التوزيع الحقيقية ، نحتاج إلى تكرار التجربة عدة مرات ومتوسط النتائج.
أضف 10 كرات حمراء و 10 كرات خضراء إلى حقيبة (أخطاء). كرر التجربة 10 مرات. في سحبت 5 أحمر و 5 أخضر . ربما؟ نعم. يمكننا أن نقول شيئا عن التوزيع الحقيقي - لا. ما يجب القيام به - حسنا ، أنت تفهم.
لفهم بنية توزيع الاحتمالات ، من الضروري أن يتم بشكل متكرر أخذ عينات فردية من هذا التوزيع ومتوسط النتائج.
نحن نربط النظرية بالممارسة
الآن ، بدلاً من الكرات السوداء والبيضاء ، دعنا نأخذ كرات البلياردو ونضع في الكيس 1000 كرة برقم 2 ، 1000 برقم 7 و 10 كرات بأرقام أخرى . تخيل مجربًا تم تدريبه في خطوات بسيطة (احصل على كرة ، اكتب الرقم ، ضع الكرة في الكيس ، امزج الكرات في الكيس) وهو يقوم بذلك في 150 ميكروثانية. حسنا ، هذا مجرب على المساعدات (وليس الإعلان عن المخدرات!). ثم في 150 ثانية سيكون قادراً على إجراء تجربتنا مليون مرة وتزويدنا بنتائج المتوسط.
جلسوا المجرب ، أعطوا الكيس ، انصرفوا ، انتظروا 150 ثانية - استلموا:
عدد 2 - 49.5 ٪ ، رقم 7 - 49.5 ٪ ، والأرقام المتبقية في المبلغ - 1 ٪.
نعم ، هذا صحيح ، حقيبتنا هي كمبيوتر الكم مع خوارزمية تحل مشكلتنا ، والكرات هي الحلول الممكنة. نظرًا لوجود حلين صحيحين ، فإن الكمبيوتر الكمي يعطينا على الأرجح أيًا من هذه الحلول الممكنة ، وأخطاء بنسبة 0.5٪ (10/2000) ، والتي سنتحدث عنها لاحقًا.
للحصول على نتيجة كمبيوتر الكم ، تحتاج إلى تشغيل خوارزمية الكم مرارا وتكرارا على نفس مجموعة بيانات الإدخال ومتوسط النتيجة.
قابلية الكمبيوتر الكم
الآن دعونا نتخيل أنه بالنسبة لمشكلة يشارك فيها 100 شخص (نتذكر مساحة القرار 2 ^ 100 ) ، لا يوجد سوى حلين صحيحين. ثم ، إذا أخذنا 100 بتة وكتبنا خوارزمية تحسب وظيفتنا الموضوعية (L ، انظر أعلاه) على هذه الكميات ، فسنحصل على كيس يحتوي على 1000 كرة برقم الإجابة الصحيحة الأولى ، 1000 مع رقم الإجابة الصحيحة الثانية و 10 كرات مع أرقام أخرى. وسيعطينا مجربنا في نفس 150 ثانية تقديراً للتوزيع الاحتمالي للإجابات الصحيحة .
يمكن اعتبار وقت تنفيذ خوارزمية الكم (مع بعض الافتراضات) ثابتًا O (1) فيما يتعلق بأبعاد مساحة الحل (2 ^ N).
وهذا هو بالضبط خاصية الكم للكمبيوتر - ثبات وقت التنفيذ فيما يتعلق بتعقيد مساحة القرار الذي ينمو وفقا لقانون السلطة هو المفتاح.
Qubit والعوالم المتوازية
كيف يحدث هذا؟ ما الذي يسمح للكمبيوتر الكمومي بإجراء حسابات بهذه السرعة؟ الأمر كله يتعلق بالطبيعة الكمومية للبت.
انظر ، قلنا أن الكوبيت ككائن كمي يدرك إحدى حالتيه عندما يتم ملاحظته ، ولكن في "الطبيعة الحية" يكون في تراكب الحالات ، أي أنه في كلتا الحالتين الحدوديتين في نفس الوقت (مع بعض الاحتمالات).
خذ (أ) ندري وتخيل حالته (التي تكون فيها السيارة 0 أو 1) كغريبة. ثم لدينا (في حيز كمي) عالمين متوازيين ، في واحد (أ) يجلس في سيارة أجرة 0 ، في عالم آخر - في سيارة أجرة 1. في نفس الوقت في سيارة أجرة اثنين ، ولكن مع بعض فرصة للعثور عليه في كل منهما عند المراقبة.
خذ (B) olod وتخيل حالته أيضًا على أنها مبتلة. عالمين متوازيين آخرين تنشأ. ولكن في حين أن هذه الأزواج من العالمين (أ) و (ب) لا تتفاعل بأي شكل من الأشكال. ما الذي يجب القيام به لإنشاء نظام متصل ؟ هذا صحيح ، تحتاج إلى الاتصال (الخلط) هذه البتات. نحن نأخذ ونخلط بين (أ) و (ب) - نحصل على نظام كم من اثنين من البتات (أ ، ب) ، والذي ينفذ أربعة عوالم متوازية مترابطة داخل نفسه. أضف (C) erge واحصل على نظام مكون من ثلاثة وحدات بت (ABC) ، والذي ينفذ ثمانية عوالم متوازية مترابطة .
إن جوهر الحوسبة الكمومية (تنفيذ سلسلة من البوابات الكمومية على نظام من البتات المزدوجة) هو حقيقة أن الحساب يتم في جميع العوالم المتوازية في وقت واحد.
وبغض النظر عن عدد منهم ، 2 ^ 3 أو 2 ^ 100 ، سيتم تنفيذ خوارزمية الكم في وقت محدد على كل هذه العوالم المتوازية وتعطينا النتيجة ، وهي عينة من التوزيع الاحتمالي لإجابات الخوارزمية.
لفهم أفضل ، يمكننا أن نتخيل أن الكمبيوتر الكمومي على مستوى الكم يبدأ عمليات القرار المتوازي 2 ^ N ، كل منها يعمل على خيار واحد ممكن ، ثم يجمع نتائج العمل ويعطينا الجواب في شكل تراكب الحل (توزيع الاحتمالات للأجوبة) ، من التي نأخذها مرة واحدة في كل مرة (في كل تجربة).
تذكر الوقت الذي يستغرقه مجربنا (150 )s) لإجراء التجربة ، وسوف يأتي هذا مفيدًا قليلاً عندما نتحدث عن المشكلات الرئيسية لأجهزة الكمبيوتر الكمومية ووقت فك الارتباط.
خوارزميات الكم
(للمحتويات)
كما ذكرنا سابقًا ، لا تنطبق الخوارزميات التقليدية القائمة على المنطق الثنائي على كمبيوتر الكم الذي يستخدم المنطق الكمومي (البوابات الكمومية). بالنسبة له ، كان عليه أن يأتي بأخرى جديدة تستفيد بالكامل من الإمكانات الكامنة في الطبيعة الكمومية للحوسبة.
الخوارزميات الأكثر شهرة اليوم هي:
على عكس أجهزة الكمبيوتر الكلاسيكية ، ليست أجهزة الكمبيوتر الكمومية عالمية.
حتى الآن ، تم العثور على عدد صغير فقط من خوارزميات الكم. (C)
بفضل oxoron على الارتباط بحديقة حيوان خوارزمية الكم ، وهو المكان الذي يجتمع فيه أفضل ممثل للعالم الخوارزمي ، وفقًا للمؤلف ( ستيفن جوردان ) ويستمر في التجمع.
في هذه المقالة ، لن نقوم بتحليل الخوارزميات الكمومية بالتفصيل ، فهناك الكثير من المواد الممتازة على الويب لأي مستوى من التعقيد ، ولكن لا تزال بحاجة إلى استعراض الخوارزميات الثلاثة الأكثر شهرة لفترة وجيزة.
خوارزمية شور.
(للمحتويات)
خوارزمية الكم الأكثر شهرة هي خوارزمية Shor (اخترعها عالم الرياضيات الإنجليزي بيتر شور في عام 1994) ، والتي تهدف إلى حل مشكلة تحليل الأرقام إلى عوامل رئيسية (مشكلة التعميق ، اللوغاريتم المنفصل).
يتم استخدام هذه الخوارزمية كمثال عندما يكتبون أنه سيتم اختراق الأنظمة المصرفية وكلمات المرور الخاصة بك قريبًا. بالنظر إلى أن طول المفاتيح المستخدمة اليوم لا يقل عن 2048 بت ، فإن وقت الحد الأقصى لم يحن بعد.
حتى الآن ، كانت النتائج أكثر من متواضعة. أفضل نتائج للمعاملات باستخدام خوارزمية Shore هي الأعداد 15 و 21 ، أي أقل بكثير من 2048 بت. بالنسبة للنتائج المتبقية من الجدول ، تم استخدام خوارزمية حساب مختلفة ، ولكن حتى أفضل النتائج وفقًا لهذه الخوارزمية (291311) ليست بعيدة عن التطبيق الحقيقي.
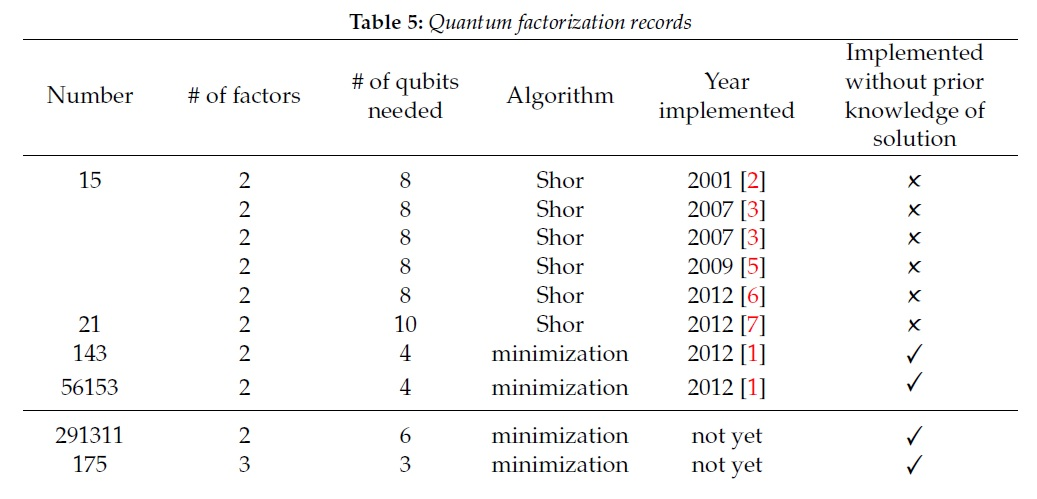
يمكنك قراءة المزيد حول خوارزمية Shore ، على سبيل المثال ، هنا . حول التنفيذ العملي - هنا .
واحد من التقديرات الحالية للتعقيد والطاقة اللازمة لتحديد عدد 2048 بت هو جهاز كمبيوتر مع 20 مليون بت. نحن ننام بسلام.
خوارزمية غروفر
(للمحتويات)
خوارزمية Grover هي خوارزمية كمية لحل مشكلة التعداد ، أي إيجاد حل للمعادلة F(X) = 1 ، حيث F هي دالة منطقية للمتغيرات n . اقترحه عالم الرياضيات الأمريكي لوف غروفر في عام 1996 .
يمكن استخدام خوارزمية Grover للعثور على الوسط الحسابي والحساب لسلسلة الأرقام. بالإضافة إلى ذلك ، يمكن استخدامه لحل مشاكل NP-Complete من خلال البحث الشامل بين العديد من الحلول الممكنة. قد يؤدي ذلك إلى زيادة كبيرة في السرعة مقارنة بالخوارزميات الكلاسيكية ، على الرغم من عدم توفير " حل متعدد الحدود " بشكل عام . (C)
يمكنك قراءة المزيد هنا ، أو هنا . يوجد أيضًا تفسير جيد للخوارزمية على سبيل المثال الصناديق والكرة ، ولكن للأسف ، لأسباب خارجة عن إرادتي ، لا يفتح هذا الموقع لي من روسيا. إذا تم حظر موقعك أيضًا ، فهناك ضغط قصير:
خوارزمية غروفر. تخيل أن لديك N قطعة من صناديق مغلقة مرقمة. كلها فارغة باستثناء تلك التي تقع فيها الكرة. مهمتك: لمعرفة عدد الصندوق الذي توجد فيه الكرة (غالباً ما يُشار إلى هذا الرقم غير المعروف بالحرف w).

كيفية حل هذه المشكلة؟ , , . , ? N/2. , 100 , 100 , , .
. , , (Oracle). — « 732», « 732 ». , , « , »
, , , : N SQRT(N) !
.
-
( )
— ( — ) — [ ]( https://ru.wikipedia.org/wiki/%D0%9A%D0%B2%D0%B0%D0%BD%D1%82%D0%BE%D0%B2%D1%8B%D0%B9 %D0%B0%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%82%D0%BC), 1992 , , . _
— , F(x1, x2, … xn) ( 0, 1 ) ( 0, 1). , , . ()
. :
( — ) , . , . : «» «» – , «», «» — . , , – . ()
( )

, . ( ) :
“ ”, .
:
( )
N+1 .
, , ( ) . , , — .
, (-273.14 ) - , () .
, , .
.
, . — IBM IBM Q System One Google Sycamore . , (2) 200 .
Sycamore, — 1 200 , — 130 . 150 . ? .
?
, 150 N — .
:
150 . — .
...
( )

, , 100% , - . , . :
, , , . , , . , , , .
— () , , , . — “ ?” — 5050, .
, ( ) - . . N 1 .
— . , 100 , 80 , 20.
— , . .
. , — IBM IBM Q System One Google Sycamore :
— . 1-Fidelity. , 2- .
2016 NQIT .
( )

, . () , , .
1- , , 12-, , , . , , , , .
, , , “ ” “” . .
:
, , . , , . - , .
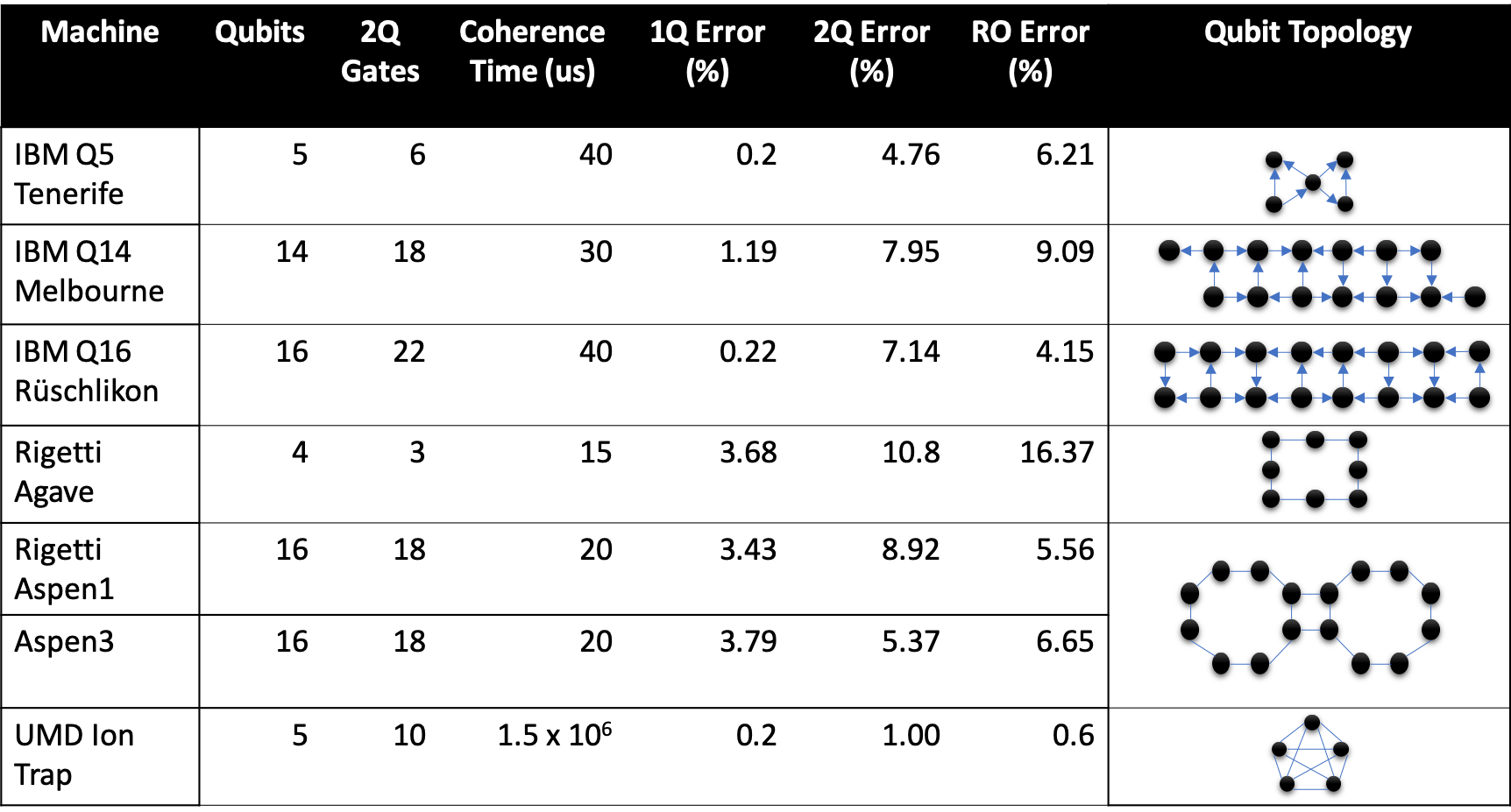
:
( )
— . 150 :
, 0.5 , :
We measure a qubit coherence time in excess of 0.5 s, and with magnetic shielding we expect this to improve to be longer than 1000 s
, , .
, , , .
, , , 1 4 1 6.
( )
, :
, , ( ) , . ( ), , .
D-Wave
( )

2000- D-Wave 2000Q. : D-Wave Systems
Google 53- , D-Wave, , . , 53 , 2048 ? ...
( ):
D-Wave ( ), , .
, , , (, ), Scott Aaronson . , ,
D-Wave. , 2014 IBM , D-Wave . , 2015 Google NASA , , , . Google , , .
, D-Wave, . , . , — . , D-Wave ASIC .
( )
. , :
- , 232 264 (8-16 )
- N 2^N , .. 2^(3+N) 32- 2^(4+N) 64- .
- N 2^N x 2^N
:
()
, Summit ( Top-1 Top-500 ) 2.8 .
— 49 ( Sunway Taihu Light )
.
. :
— 49 - 39 "" ( ) 2^63 — 4 4
50+ . - Google 53- .
.
( )

:
́ ́ — , .
, , , , , . .
, “ ”. , 50+ , , , . .
, . , Google, Sycamore .
Google
( )

54- Sycamore
, 2019 Google Nature « ». 54- «Sycamore».
Sycamore 54- , 53-. , , 54- , . , 53- .
, .
IBM , Google . , 2,5 , , . .
, , Scott Aaronson . Scott's Supreme Quantum Supremacy FAQ! , . FAQ, , , .
Google? , :
, , , . : (.. 1- 2- — — , 20, 2D n=50-60 ). , 0, {0,1}, n- () . , , .
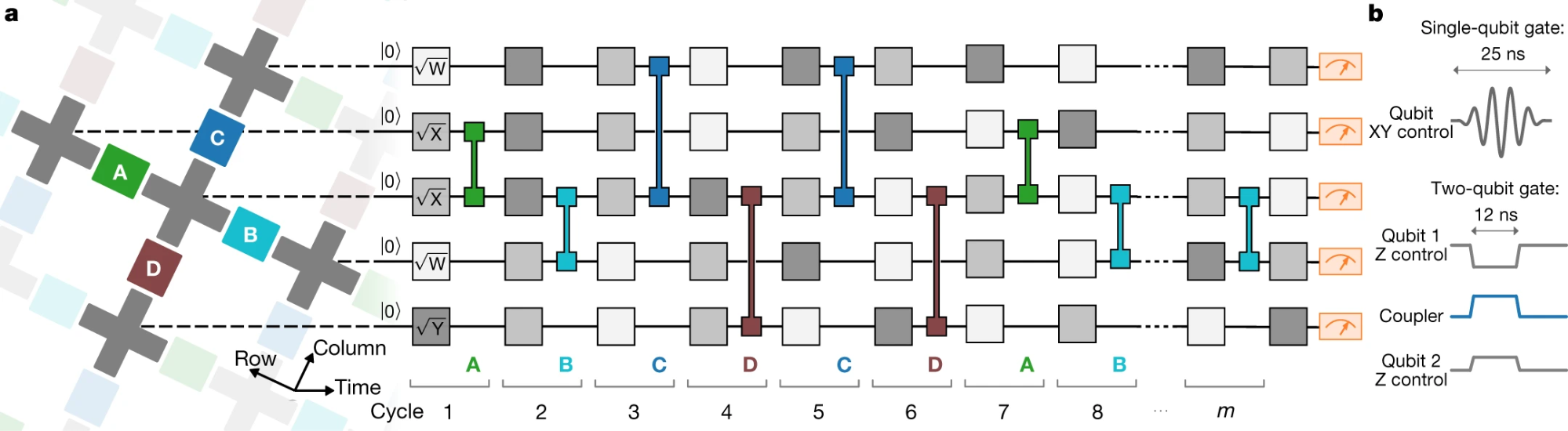
:
Google 53- , .
— Google , , , , , . , 2048- .
ملخص
( )

— , .
(-) :
:
:
:
( ), , - , .
— , , . .
استنتاج
( )
, , , , D-Wave Google .
(, , ..) , , , , .. , .
, - .
() Kruegger
( )

@Oxoron , “ ”
@a5b - “ ” , , .
, .
( )

[The National Academies Press]