أدت دراسة النيوتريونات إلى اكتشاف غير متوقع في الرياضيات

أراد ثلاثة علماء في الفيزياء حساب عملية تغيير النيوتريونات. نتيجة لذلك ، وجدوا علاقة غير متوقعة بين بعض الأشياء الأكثر شيوعًا في الرياضيات.

ذات يوم في أغسطس ، في صباح اليوم التالي للإفطار ، افتتح عالم الرياضيات تيرنس تاو رسالة بريد إلكتروني كتبها ثلاثة علماء في الفيزياء لم يكن يعرفهم. أوضحت لها الثالوث أنها تعثرت في صيغة بسيطة ، والتي ، إذا كانت صحيحة ، ستصف علاقة غير متوقعة بين بعض الأشياء الأساسية والهامة للجبر الخطي.

وقال تاو ، الأستاذ بجامعة كاليفورنيا في لوس أنجلوس ، وهو أحد رواد الحقول ، أحد علماء الرياضيات الرائدين في العالم ، "الصيغة تبدو جيدة للغاية". وقال "شيء قصير وبسيط كان ينبغي أن يكون في الكتب المدرسية منذ وقت طويل". "لذلك ، في البداية فكرت - لا ، هذا لا يمكن أن يكون."

ثم فكر أكثر من ذلك بقليل.

فيزيائيون - ستيفن بارك من المعمل الوطني للتسريع. حصل فيرمي ، شينينغ زهانج من جامعة شيكاغو وبيتر دنتون من مختبر بروكهافن الوطني - على هذه الهوية الرياضية قبل شهرين ، في محاولة للتعامل مع السلوك الغريب للجزيئات الأولية التي تسمى النيوتريونات .

لقد لاحظوا أن " عوامل التكاثر" ، التي يصعب حسابها ، والتي تصف في حالتهم كيفية انتشار النيوتريونات في المادة ، تُعادل بمجموعة من المصطلحات المعروفة باسم "القيم الذاتية" ، والتي يسهل حسابها. علاوة على ذلك ، فقد أدركوا أن هذه العلاقة بين المستحثات الذاتية والقيم الذاتية - أشياء شائعة جدًا في الرياضيات والفيزياء والهندسة ، والتي تمت دراستها منذ القرن الثامن عشر - تبدو ذات ترتيب عام.

على الرغم من أن الفيزيائيين لم يصدقوا أنهم اكتشفوا حقيقة جديدة تتعلق بهذه الرياضيات الأساسية ، إلا أنهم لم يتمكنوا من إيجاد مثل هذه العلاقة سواء في الكتب أو في المقالات. لذلك ، قرروا اغتنام الفرصة والاتصال بـ Tao ، على الرغم من تقديم طلب على موقع الويب الخاص به لعدم إزعاجه في مثل هذه الحالات.

قال بارك: "لمفاجأتنا ، أجاب بعد ساعتين ، وقال إنه لم يسبق له مثيل من قبل". وإلى جانب ذلك ، في إجابة تاو كان هناك ثلاثة أدلة مستقلة على هذه الهوية.


شينينغ زانج وبيتر دنتون وستيفن بارك مع تركيبة مفتوحة

بعد أسبوع ونصف ، قام الفيزيائيون وتاو ، الذين يطلق عليهم بارك اسم "خرطوم الحريق في الرياضيات" ، بنشر ورقة على شبكة الإنترنت تبلغ عن صيغة جديدة. الآن يتم تقييم هذا العمل من قبل المتخصصين في مجلة الاتصالات في الفيزياء الرياضية. في ورقة منفصلة نشرت في مجلة فيزياء الطاقة العالية ، استخدم Denton و Park و Zhang هذه الصيغة لتبسيط المعادلات التي تصف سلوك النيوترونات.

يقول الخبراء إن هذه الصيغة قد يكون لها طرق أكثر للتطبيق ، لأنه في عدد كبير من المهام ، يلزم حساب عوامل الاستنتاج والقيم الذاتية. وقال جون بيكوم ، المتخصص في فيزياء الجسيمات في جامعة أوهايو: "لها مجموعة واسعة من الاستخدامات". "من يعرف ما هي الأبواب التي يمكن أن تفتح".

يفكر علماء الرياضيات بنفس الطريقة. وقال فان وو ، عالم الرياضيات في جامعة ييل: "هذا أمر مثير للدهشة ومثير للاهتمام." "لم أكن أظن أنه كان من الممكن حساب مضادات التكاثر باستخدام معلومات فقط عن القيم الذاتية."

أثبتت فو وتاو هوية مماثلة في عام 2009 (وهذا هو السبب قرر دينتون وبارك وتشانغ الاتصال تاو) ، ولكن الصيغة الجديدة لا تتبع بوضوح من الصيغة القديمة. وعلى الرغم من ظهور صيغة مماثلة عن طريق الصدفة في عمل رياضي في شهر مايو من هذا العام ، إلا أن مؤلفيها لم يربطوها بالمُحَثِّيات الذاتية والقيم الذاتية.

بمعنى ما ، ليس من المستغرب أن تكون فكرة جديدة عن الأجسام الرياضية منذ عدة قرون تأتي من علماء الفيزياء. ألهمت الطبيعة الأبحاث الرياضية منذ أن بدأ الناس في الاعتماد على 10 أصابع. قال فو: "لكي تزدهر الرياضيات ، يجب أن تكون مرتبطة بالطبيعة". "لا توجد وسيلة أخرى."

حيل التحول

تعد عوامل التوليد والقيم الذاتية شائعة جدًا لأنها تميز التحويلات الخطية: العمليات التي تمد أو تضغط أو تدور أو تغير بأي طريقة أخرى جميع أجزاء الكائن نفسه بالتساوي. يتم تمثيل هذه التحولات بواسطة صفائف مستطيلة من الأرقام تسمى المصفوفات. مصفوفة واحدة تدور الكائن 90 درجة ؛ الآخر ينقلب رأساً على عقب وينقصه إلى النصف.


تطبيق هذه المصفوفة على كائن معين سيعكسها بالنسبة إلى المستوى ، وأيضًا مضاعفة ارتفاعها. تصف متغيرات المصفوفة الأولية الاتجاهات التي لا يتغير فيها الكائن ، باستثناء القياس. تصف القيم الذاتية للمصفوفة مقدار تحجيم الكائن على طول هذه المتغيرات الذاتية.
eigenvector A موازية للمحور العمودي. القيمة الذاتية لها هي 2 ، لأن الكائن يضاعف ارتفاعه.
يقع eigenvector B في مستوى الانعكاس. القيمة الذاتية لها هي 1 ، لأن الكائن لا يتغير على طوله.
Eigenvector C عمودي على مستوى الانعكاس. قيمها الذاتية هي -1 ، مما يعني انعكاس نسبة إلى الطائرة.
عن طريق حذف صفوف وأعمدة المصفوفة ، يمكن إنشاء مصفوفات أصغر. يمكن استخدام القيم الذاتية المتماثلة مع القيم الذاتية للمصفوفات الأصلية لحساب المتجهات الذاتية للمصفوفات الأصلية.

تقوم المصفوفات بذلك عن طريق تغيير "المتجهات" للكائنات - أسهم رياضية تشير إلى كل مكان مادي للكائن. المتجهات الذاتية للمصفوفة هي تلك المتجهات التي تستمر في الإشارة في نفس الاتجاه كما كان من قبل ، بعد تطبيق المصفوفة. لنفترض أننا نأخذ مصفوفة تدور كائنًا بزاوية 90 درجة حول المحور السيني: يتم توجيه المتجهات الذاتية على طول المحور السيني ، نظرًا لأن النقاط الموجودة على هذا المحور لا تدور عندما تدور البقية حولها.

يمكن لمصفوفة مماثلة تدوير الكائنات حول المحور س وضغطها مرتين. إلى أي مدى تضغط المصفوفة أو تمدد المتجهات الذاتية للكائن ، تصف القيم المتماثلة المتناظرة - في هذه الحالة ، 1/2 (إذا لم يتغير المتغير المستقل ، تكون القيمة المتماثلة الأولية الخاصة به هي 1).


تيرينس تاو

تكون وحدات التهيئة الذاتية والقيم الذاتية مستقلة ، وعادة ما يجب حسابها بشكل منفصل ، بدءًا من الصفوف والأعمدة في المصفوفة نفسها. يتعلم الطلاب القيام بذلك لمصفوفات بسيطة. لكن الصيغة الجديدة تختلف عن الأساليب الحالية. وقال تاو "الأمر المثير للاهتمام في هذه الهوية هو أنك لست بحاجة إلى معرفة أي قيم موجودة في المصفوفة من أجل حساب شيء ما".

يتم تطبيق الهوية على مصفوفات هيرميت التي تقوم بتحولات حقيقية من متغيرات eigenvector (على عكس الأرقام وهمية) ، وبالتالي ، تنطبق على المواقف التي تحدث في الواقع. تعبر الصيغة عن كل متجانس من المصفوفة الهرمية من حيث القيم الذاتية لهذه المصفوفة و "المصفوفة الثانوية" - مثل مصفوفة أصغر ، والتي يتم الحصول عليها عن طريق حذف الصف والعمود من الأصل.

وقال تاو: "إذا نظرنا إلى الوراء ، فإن الصيغة تبدو معقولة ، لأن القيم الذاتية للمصفوفة الثانوية تشفر المعلومات المخفية في حد ذاتها. ومع ذلك ، "على سبيل المثال ، أنا شخصيا لم أفكر أبدا في شيء من هذا القبيل."

وقال إن أداة لا علاقة لها مهمة نادرا ما تظهر في الرياضيات. ومع ذلك ، فهو يعتقد أن الترابط بين القيم الذاتية والقيم الذاتية يجب أن يكون مهمًا. وقال "إنها جميلة لدرجة أنني متأكد من أن المعادلة ستجد بعض التطبيق في المستقبل القريب". "حتى الآن ، لدينا استخدام واحد لها فقط."

جزيئات بالذئب

ويرتبط هذا التطبيق مع النيوتريونات: أغرب وأقل درس وأكثر سرية من الجزيئات الأساسية المعروفة. في كل ثانية ، تمر تريليونات من هذه الجسيمات عبر جسم الإنسان ، ولكن بما أنها لا تظهر وجودها عمليا ، فإن الكثير من خصائصها تظل غير معروفة.

ومن المثير للاهتمام ، أن النظرية تدعي أن الاختلافات في سلوك النيوتريونات ومضادات النيوترونات بالضبط هي التي يمكن أن تتسبب في هيمنة المادة على المادة المضادة في الكون . إذا ظهر الأضداد بكميات متساوية بعد الانفجار الكبير ، فسوف يهلك كل منهما الآخر ، ولن يتبقى في الفضاء سوى الضوء. يمكن أن يؤدي الاختلاف بين النيوترينو ومضادات الإلتهاب إلى زيادة حيوية في المادة. وقالت ديبورا هاريس ، عالِمة الفيزياء بجامعة يورك وفيرميلاب ، التي تعمل في تجربة DUNE (تجربة ديب أندرراوند نيوترينو ، وهي نيوترينو عميقة تحت الأرض): "إذا تصرفوا بطريقة مختلفة ، فسوف يعطينا فكرة عن سبب امتلاء الكون بالمادة". التجربة) مصممة لقياس مثل هذه الاختلافات.

تستخدم التجربة ، التي تقيس خصائص النيوتريونات التي تم إطلاقها من فيرميلاب في إلينوي إلى جهاز كشف تحت الأرض يقع على بعد 1300 كم من المصدر في ساوث داكوتا ، حقيقة أن هناك ثلاثة أنواع مختلفة من النيوتريونات - الإلكترون ، والميون ، والتاو. ومع ذلك ، فإن كل نوع هو خليط ميكانيكي الكم ، ويتأرجح النيوتريونات ، وتغيير أنواعها أثناء التنقل. عندما تنتقل النيوتريونات من فيرميلاب ، يتغير خليطها ، لذلك يمكن أن يتحول الميون نيوترينو إلى إلكترون أو تاو نيوترينو.

يتم وصف هذه التذبذبات بمصفوفة 3x3 معقدة للغاية. استنادًا إلى عوامل التثبيط والقيم الذاتية ، يمكن للفيزيائيين حساب تعبير يصف احتمال أن يتحول نيوترينو الميون إلى نيوترينو إلكتروني بحلول وصوله إلى ساوث داكوتا. كما أنهم يحسبون احتمالية أن يصبح الميون نيوترينو مضادًا للإلكترون.


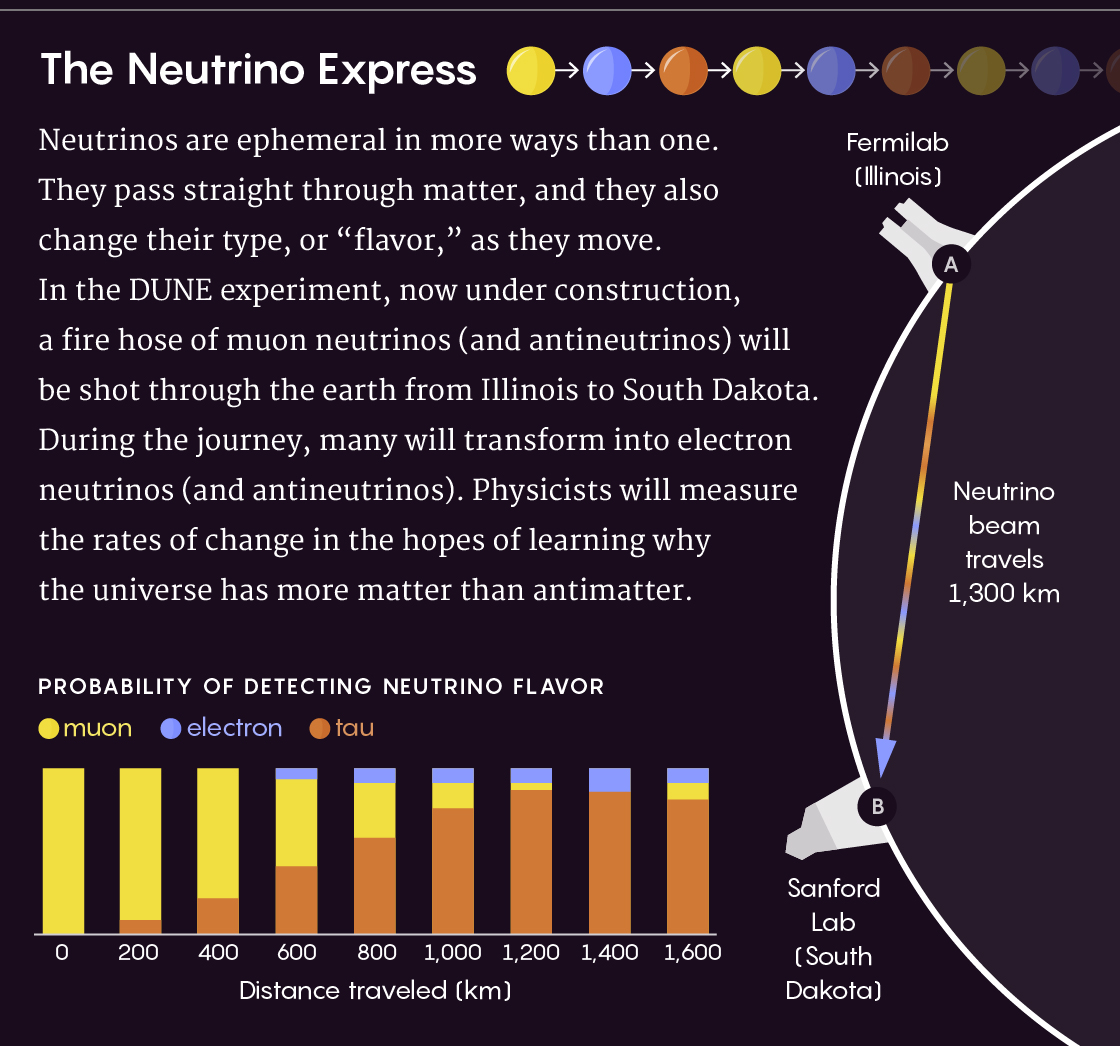لا تمر جسيمات النيوترينو سريعة الزوال عبر المادة فحسب ، بل تغير أيضًا نوعها أثناء الطيران. في تجربة DUNE ، سيتم إطلاق حزمة النيوترينو ، سيغير الكثير منها أنواعها في الطريق من المصدر إلى الهدف. سيتم قياس هذه التغييرات بواسطة علماء الفيزياء.
يوضح الرسم البياني احتمال اكتشاف النيوتريونات بأنواعها المختلفة حسب مسافة السفر بالكيلومتر. الأصفر - muon ، الأزرق - الإلكترونية ، البني - تاو.

تحتوي هذه التعبيرات على المجهول: "مرحلة انتهاك ثبات CP " ، والتي توضح كيف تختلف قوانين التذبذبات المضادة للنيوترينو ومضادات التريوتين عن بعضها البعض. من خلال قياس ومقارنة نسب التذبذب الحقيقية ، يمكن للعلماء الذين يحملون DUNE حساب هذا المجهول. إذا كانت مرحلة الاضطراب كبيرة بدرجة كافية ، فسيساعد ذلك في توضيح سبب امتلاء الكون بالمادة.

وكما لو أن هذه الصعوبات ليست كافية ، فإن أحد الآثار الغريبة ، التي اكتشفها الفيزيائي لنكولن ولفنشتاين لأول مرة عام 1978 ، تجعل مصفوفة النيوترينو أكثر تعقيدًا. نادراً ما يتفاعل النيوتريونات مع المادة بالمعنى المعتاد ، لكن ولفينشتاين وجد أن مرورها عبر المادة ، على عكس الفضاء الفارغ ، لا يزال يغير الطريقة التي ينتشر بها. في بعض الأحيان يتفاعل اختراق النيوترينو خلال المادة مع الإلكترونات في ذرة ، مما يؤدي في الأساس إلى تغيير الأماكن: يتحول النيوترينو الإلكتروني إلى إلكترون والعكس بالعكس.

هذه البدائل تقدم مصطلحًا جديدًا في المصفوفة ، مما يؤثر على النيوتريونات الإلكترونية ، مما يعقد الرياضيات إلى حد كبير. هذا هو تأثير ميكيف - سميرنوف - ولفنشتاين [الذي تم التنبؤ به من قبل علماء الفيزياء السوفيتيين ستانيسلاف ميكيف وأليكسي سميرنوف في عام 1985 على أساس حالة تذبذبات النيوترينو في وسط مع كثافة ثابتة في ولفينشتاين] دفعت بارك ، وتشانغ ، ودنتون .

إن تعبير حساب القيم الذاتية أبسط من التعبير عن القيم الذاتية ، لذلك استخدم بارك وتشانغ ودنتون هذا كنقطة انطلاق. قبل ذلك ، قاموا بتطوير طريقة جديدة لحساب القيمة التقريبية للقيم الذاتية. واستنادا إلى ذلك ، لاحظوا أن التعبيرات الطويلة لعوامل الاستنتاج من الأعمال السابقة كانت مساوية لمجموعات هذه القيم الذاتية. قال تشانغ إن وضع كل ذلك معًا "يمكنك بسهولة وبسرعة حساب التذبذبات النيوترينية في المادة".

فيما يتعلق بكيفية رؤية النموذج الذي تتبعه الصيغة ، فإن الفيزيائيين ليسوا متأكدين تمامًا. يقول بارك إنهم لاحظوا ببساطة المظاهر الفردية للنمط وقاموا بتعميمه. كما يعترف بأنه يجيد حل الألغاز. شارك في تأليف كتاب انتظام مهم آخر ، اكتشف عام 1986 ، والذي سهل الحسابات في مجال فيزياء الجسيمات ، وحتى يومنا هذا يلهم العلماء لاكتشافات جديدة.

ومع ذلك ، فإن حقيقة أن السلوك الغريب للنيوترينو يمكن أن يؤدي إلى ظهور أفكار جديدة تتعلق بالمصفوفة صدمت الكثيرين. "لقد تم حل الناس الجبر الخطي لفترة طويلة جدا جدا" ، وقال بارك. "ما زلت أنتظر أن يقوم شخص ما بإرسال رسالة بريد إلكتروني لي فيها: إذا نظرت إلى هذا العمل غير المعروف لـ Cauchy ، فهناك هذه الصيغة في الملاحظة على الملحق الثالث."

فرق بسيط

في الواقع ، كانت هناك صيغة مماثلة معروفة بالفعل ، لكن لم يلاحظها أحد ، لأنها كانت ملثومة.

في سبتمبر ، تلقى Tao بريدًا إلكترونيًا آخر غير متوقع ، هذه المرة من Jiyuan Zhang ، وهو طالب دراسات عليا في الرياضيات من جامعة ملبورن في أستراليا. أشار تشانغ إلى وجود صيغة معادلة في عمل كتبه مع أمينه بيتر فورستر في مايو ، قبل ظهور عمل تاو وثلاثة فيزيائيين. عمل تشانغ وفوريستر في مجال الرياضيات البحتة ، نظرية المصفوفات العشوائية. طبقوا هذه الصيغة ، واستكشفوا المشكلة المرتبطة بحل تاو وزملائه في عام 1999.

أوضح لنا فورستر أنه لأول مرة ظهرت هذه الصيغة في شكل آخر في عمل عام 2001 ، من تأليف جوليا باريشنيكوفا ، عالم رياضيات تعمل الآن في جامعة إلينوي في أوربانا شامبين ، والتي استندت أعمالها إلى فورستر وتشانغ. لكن هؤلاء الرياضيين وصفوا كائنات هويتهم ليس كمتغيرات ذاتية ، ولكن كمصطلحات ضرورية لحساب القيم الذاتية لبعض المصفوفات الثانوية التي تظهر في سياق حل مشكلتهم.

دعا فورستر الصيغة في عمله مع تشانغ "مماثلة" لتلك المستخدمة من قبل تاو والفيزيائيين الثلاثة. ووصف تاو الصيغ بأنها "متطابقة تقريبًا" ، مشيرًا إلى بعضهما البعض بالطريقة نفسها التي يتحدث بها الجانبان عن وهم الأرنب / البط. "بعض الناس بحثوا عن الأرانب ، والبعض الآخر بحث فقط عن البط" ، قال.



كتب دنتون في رسالة بالبريد الإلكتروني أن الصيغة التي كانت موجودة من قبل "قريبة من نتيجتنا ، ولكنها ليست مثالية". وأضاف أنه "في ضوء أهمية المتجهات الذاتية للعديد من المشكلات ، ما زلنا نعتقد أن نتائجنا مختلفة تمامًا عن الباقي لاعتبارها جديدة".

ربما ليس غريباً أن يحدث هذا الإثارة المفاجئة في هذا المجال في صيف واحد بعد عدة قرون. وقال تاو "هناك العديد من الأمثلة على الاكتشافات المتزامنة في الرياضيات". - النتائج معلقة بطريقة ما في الهواء. ويبدأ الناس في البحث عنهم في الأماكن المناسبة. "