كتبت ذات مرة
مقالة وصفت فيها نموذجًا رياضيًا بسيطًا لتطور الشبكة العصبية واختيارها للقدرة على إضافة أرقام في أنظمة الأرقام ذات القواعد 2 والنسبة الذهبية ، واتضح أن النسبة الذهبية تعمل بشكل أفضل. لذلك ، تبين أن تجربتي الأولى كانت سيئة للغاية ، حيث أنني لم أضع في الاعتبار عددًا من الفروق الدقيقة المهمة المتعلقة بحقيقة أن الخطأ لا ينبغي أن يؤخذ في الاعتبار بالنسبة للخلية العصبية ، ولكن بالنسبة إلى القليل من المعلومات ، لذلك قررت تحسين تجربتي ، وأقدم عددًا قليلاً منها التعديلات.
- قررت فحص 100 زوج من عينات مكونة من 15 (عينة تدريب) و 1000 (عينة اختبار) متجه في أنظمة الأرقام ذات قواعد موزعة بشكل موحد من 1-2 إلى 2 بدلاً من قاعدتين معروفتين سابقًا.
- لقد قمت أيضًا بتحول خطي ليس فقط من المسافة من القاعدة إلى النسبة الذهبية ، ولكن أيضًا من القاعدة نفسها ، وعدد الإحداثيات في المتجه ومتوسط قيمة الإحداثيات في متجه الاستجابة ، لأخذ في الاعتبار الاعتماد غير الخطي للخطأ على القاعدة.
- لقد راجعت أيضًا بعض العينات للتأكد من طبيعتها وفقًا لمعيار كولموجوروف-سميرنوف ، ANOVE ، لكن هذه المعايير أظهرت أن العينات من المرجح أن تنحرف عن الغاوسي ، لذلك قررت أن تجعل الانحدار الخطي الموزون بدلاً من المعتاد. ومع ذلك ، ANOVA ، على الرغم من أنها أظهرت F أقل بقليل من ذي قبل (في منطقة 700-800 بدلاً من 800-900) ، ولكن لا تزال النتيجة أكثر من ذات دلالة إحصائية ، مما يعني أنه يجب إجراء المزيد من الاختبارات. أثناء هذه الاختبارات ، أخذت رسم بياني لكثافة توزيع مخلفات الانحدار و QQ العادي - رسم بياني لوظيفة التوزيع لهذه المخلفات.
هذه الرسوم البيانية هما:
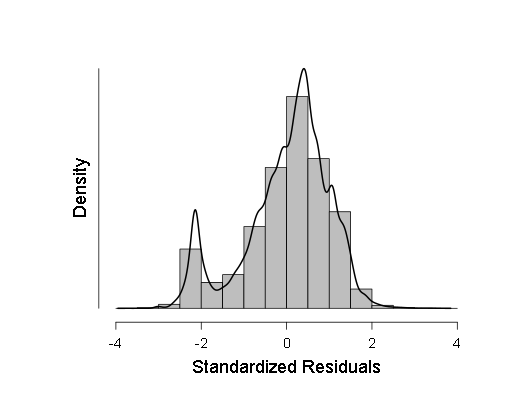
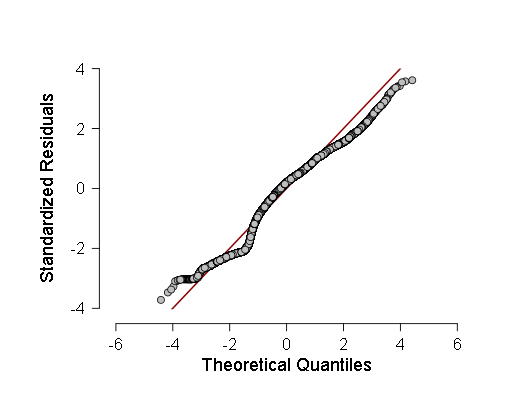
كما يمكن أن نرى ، على الرغم من أن الانحراف عن التوزيع الطبيعي في توزيع البقايا له دلالة إحصائية (وعلى اليسار ، حتى وضع ثانٍ صغير مرئي على الرسم البياني) ، في الواقع أنه قريب جدًا من غاوسي ، لذلك ، من الممكن (بحذر وفواصل ثقة أكبر) الاعتماد على هذا الانحدار الخطي .
الآن عن كيفية إنشاء عينات لاختبار الشبكات العصبية عليها.
هنا هو رمز لتوليد العينات: وهنا هو رمز ملف الرأس: #include <stdio.h> #include <stdlib.h> #include <math.h> int main(void); void calculus(double a, double x, bool *t, int n);// x a t n . void calculus(double a, double x, bool *t, int n) { int i,m,l; double b,y; b=0; m=0; l=0; b=1; int k; k=0; i=0; y=0; y=x; // t . for (i=0;i<n;i++) { (*(t+i))=false; } k=((int) (log((double)2))/(log(a)))+1;// , . while ((l<=k-1)&&(m<nk-1)) // x a ( ), { m=0; if (y>1) { b=1; l=0; while ((b*a<y)&&(l<=k-1)) { b=b*a; l++; } if (b<y) { y=yb; (*(t+kl))=true; } } else { b=1; m=0; while ((b>y)&&(m<nk-1)) { b=b/a; m++; } if ((b<y)||(m<nk-1)) { y=yb; (*(t+k+m))=true; } } } return; }
قررت أيضًا نشر الرمز الكامل للشبكة العصبية: بعد ذلك ، دعونا نتحدث عن كيفية إجراء الانحدار الخطي الموزون. للقيام بذلك ، قمت ببساطة بحساب الانحرافات المعيارية لنتائج الشبكة العصبية ، ثم قسّمت الوحدة إليها.
فيما يلي الكود المصدري للبرنامج الذي قمت به بهذا: #include <stdio.h> #include <stdlib.h> #include <math.h> int main(void) { int i; FILE *input,*output; while (fopen("input.txt","r")==NULL) i=0; input = fopen("input.txt","r");// . double mu,sigma,*x; mu=0; sigma=0; while (malloc(1000*sizeof(double))==NULL) i=0; x = (double *) malloc(sizeof(double)*1000); fscanf(input,"%lf",&mu); mu=0; for (i=0;i<1000;i++) { fscanf(input,"%lf",x+i); } for (i=0;i<1000;i++) { mu = mu+(*(x+i)); } mu = mu/1000; while (fopen("WLS.txt","w") == NULL) i=0; output = fopen("WLS.txt","w"); for (i=0;i<1000;i++) { sigma = sigma + (mu - (*(x+i)))*(mu - (*(x+i))); } sigma = sigma/1000; sigma = sqrt(sigma); sigma = 1/sigma; fprintf(output,"%10.9lf\n",sigma); fclose(input); fclose(output); free(x); return 0; };
بعد ذلك ، أضفت الأوزان الناتجة إلى الجدول ، حيث قمت بتقليل جميع البيانات التي تم الحصول عليها نتيجة للبرنامج ، وكذلك قيم المتغيرات لحساب الانحدار ، ثم قمت بحسابها في JASP. وهنا النتائج:
النتائج
الانحدار الخطي
بعد ذلك ، لدي رسم بياني لكثافة التوزيع لمخلفات الانحدار القياسية:

بالإضافة إلى الرسم البياني الكمي العادي لمخلفات الانحدار القياسي:

ثم قمت بتطبيق متوسط قيم معاملات الانحدار التي تم الحصول عليها في مسارها على المتغيرات ، وقمت بتحليلي الإحصائي لإيجاد الحد الأدنى المحتمل لوظيفة الخطأ من قاعدة نظام الأعداد (مقدار ارتباطها بهذه المتغيرات) باستخدام lemma الخاص بفيرما ونظرية Bayes ونظرية Lagrange على النحو التالي:
والحقيقة هي أن توزيع قواعد نظام الأرقام في العينة كان واضحًا بشكل موحد ، لذلك ، إذا كانت قاعدة معينة في الفاصل (1،2 ؛ 2) هي الحد الأدنى للخطأ المتوسط المربّع ، عندئذٍ ، بواسطة lemma لـ Fermat ، سيكون له مشتق صفري ، ثم كثافة الاحتمالية للقيم سوف تكون وظيفة لانهائية.
الآن عن كيفية تطبيق نظرية بايز. حسبت فواصل الثقة لتوزيع بيتا (هذا هو توزيع احتمالية "النجاح" في التجربة تحت شرط "النجاحات" و "الإخفاقات" مع كثافة الاحتمالات
) قيم دالة التوزيع (هذا هو احتمال ألا يكون المتغير العشوائي أكبر من الوسيطة) للأخطاء المحسوبة ، بناءً على حقيقة أنه إذا لم يكن المتغير العشوائي أكبر من الوسيطة ، فهو "نجاح" ، وإذا كان أكثر من ذلك ، فإن "الفشل". ثم ، باستخدام نظرية بايز ، نطبق التوزيع التجريبي لوظيفة التوزيع للأخطاء المحسوبة ، ونحسب فواصل الثقة [دالة التوزيع] الخاصة بها بنسبة 99٪ في كل خطأ محسوب.
نمر إلى نظرية لاغرانج. تنص نظرية لاغرانج على أنه إذا كانت الوظيفة f (x) قابلة للتمييز بشكل مستمر على الفاصل الزمني [a؛ b] ، عند نقطة واحدة على الأقل من هذا الفاصل الزمني ، يكون لها مشتق يساوي
. كيف أطبق هذه النظرية: الحقيقة هي أن الكثافة الاحتمالية هي مشتق من وظيفة التوزيع ، لذلك تأخذ القيمة القصوى بين تلك التي تأخذها بالضبط في بعض الفواصل الزمنية من الحد الأدنى من الخطأ إلى الأخطاء المتبقية. ثم أقوم بحساب فواصل الثقة لهذه القيم في 98٪ (باستخدام تصحيح Bonferroni) باستخدام الصيغة التالية:
حيث F1 هي الطرف الأيسر من فاصل الثقة لوظيفة التوزيع ، و F2 هي اليمين ، x_i ، x_1 هي الأخطاء المحسوبة كوسيطة لدالة التوزيع. بعد ذلك ، يبحث البرنامج عن فاصل زمني مع الطرف الأيسر الأكبر والأكبر الأيمن (بحيث تكون القيمة في الفاصل الزمني الأقصى) ، ثم يبحث عن الحد الأقصى والحد الأدنى في القواعد التي تتوافق مع الأخطاء المحسوبة في هذا الفاصل الزمني. هذه الحد الأقصى والحد الأدنى هي وسيطات دالة الخطأ من أسفل ، والتي تقع بين الحد الأدنى للدالة نفسها مع احتمال 98 ٪.
فيما يلي رمز البرنامج الذي أجريته هذا التحليل الإحصائي مع شرح: وهنا هو رمز ملف الرأس: #include <stdio.h> #include <stdlib.h> #include <math.h> int main(void); double Bayesian(int n, int m, double x);// - n "" m "", " " " " , : double Bayesian(int n, int m, double x) { double c; c=(double) 1; int i; i=0; for (i=1;i<=m;i++) { c = c*((double) (n+i)/i); } for (i=0;i<n;i++) { c = c*x; } for (i=0;i<m;i++) { c = c*(1-x); } c=(double) c*(n+m+1); return c; } double Bayesian_int(int n, int m, double x);// - ( ): double Bayesian_int(int n, int m, double x) { double c; int i; c=(double) 0; i=0; for (i=0;i<=m;i++) { c = c+Bayesian(n+i+1,mi,x); } c = (double) c/(n+m+2); return c; } // : void Bayesian_99CI(int n, int m, double &x1, double &x2, double &mu); void Bayesian_99CI(int n, int m, double &x1, double &x2, double &mu) { double y,y1,y2; y=(double) n/(n+m); int i; for (i=0;i<1000;i++) { y = y - (Bayesian_int(n,m,y)-0.5)/Bayesian(n,m,y); } mu = y; y=(double) n/(n+m); for (i=0;i<1000;i++) { y = y - (Bayesian_int(n,m,y)-0.995)/Bayesian(n,m,y); } x2=y; y=(double) n/(n+m); for (i=0;i<1000;i++) { y = y - (Bayesian_int(n,m,y)-0.005)/Bayesian(n,m,y); } x1=y; }
إليكم نتيجة عمل هذا البرنامج ، عندما أعطيتها أسس نظام الأرقام ونتائج الانحدار:
x (- [1.501815; 1.663988] y (- [0.815782; 0.816937]
("(-" في هذه الحالة هو مجرد تدوين للعلامة "ينتمي" من نظرية المجموعة ، وتشير الأقواس المربعة إلى الفاصل الزمني.)
وهكذا ، اتضح لي أن أفضل أساس لنظام الأرقام من حيث أقل عدد من الأخطاء في نقل المعلومات يكمن في النطاق من 1.501815 إلى 1.663988 ، أي أن النسبة الذهبية تقع فيه بالكامل. صحيح ، لقد قمت بافتراض واحد عند حساب الحد الأدنى وواحد آخر عند حساب كمية المعلومات في أنظمة الأرقام المختلفة: أولاً ، افترضت أن وظيفة الخطأ من القاعدة مختلفة باستمرار ، وثانيًا ، أن احتمال أن يكون العدد الموزع بشكل موحد هو 1 ، سيكون الرقم من رقم 2 إلى رقم واحد في رقم محدد ، وسيكون هو نفسه تقريبًا بعد بعض الأرقام بعد العلامة العشرية.
إذا ارتكبت شيئًا خاطئًا تمامًا أو كنت مخطئًا ، فأنا منفتح على النقد والاقتراحات. آمل أن تكون هذه المحاولة أكثر نجاحًا.
UPD. قمت بتحرير المقالة مرتين لتوضيح بعض الأماكن في الجزء "العلمي المحض" ، وقمت أيضًا بتنسيق الكود.
UPD2. بعد التشاور مع شخص يفهم المعلوماتية الحيوية (خريج مدرسة الدراسات العليا في مكتب الأمن الفيدرالي بجامعة موسكو الحكومية ، ويعمل في IPPI RAS) ، تقرر استبدال كلمة "الدماغ" بكلمة "شبكة عصبية" ، نظرًا لأنها تختلف اختلافًا كبيرًا.