
الغرض من هذا المقال هو تعليم الشبكة العصبية للعب لعبة الحياة دون تعليمها قواعد اللعبة.
مرحبا يا هبر! أقدم إليكم ترجمة المقال "استخدام شبكة عصبية تلافيفية للعب لعبة كونوي للحياة مع Keras" بواسطة kylewbanks.
إذا لم تكن على دراية باللعبة المسماة Life ( هذه عبارة عن إنسان آلي خلوي اخترعه عالم الرياضيات الإنجليزي جون كونواي في عام 1970 ) ، فإن القواعد هي كما يلي.
كون اللعبة عبارة عن شبكة لا نهائية ثنائية الأبعاد من الخلايا المربعة ، كل واحدة منها في واحدة من حالتين محتملتين: حي أو ميت (أو مأهول وغير مأهول ، على التوالي). تتفاعل كل خلية مع جيرانها الثمانية أفقيا أو رأسيا أو قطريا. في كل خطوة زمنية ، تحدث التحولات التالية:
- أي خلية حية مع أقل من اثنين من الجيران الأحياء يموت.
- أي خلية حية مع اثنين أو ثلاثة من الجيران الذين يعيشون على قيد الحياة إلى الجيل القادم.
- أي خلية حية مع أكثر من ثلاثة جيران يعيشون يموتون.
- أي خلية ميتة مع ثلاثة جيران يعيشون بالضبط تصبح خلية حية.
يتم إنشاء الجيل الأول من خلال تطبيق القواعد المذكورة أعلاه في وقت واحد على كل خلية في الحالة الأولية ، وتحدث الولادة والموت في وقت واحد في نقاط منفصلة في الوقت المناسب. كل جيل هو وظيفة نقية من السابق. تستمر القواعد المطبقة على الجيل الجديد لإنشاء الجيل التالي.
انظر ويكيبيديا للحصول على التفاصيل.
لماذا هذا؟ أساسا للترفيه ، ومعرفة القليل عن الشبكات العصبية التلافيفية.
لذلك ...
منطق اللعبة
أول شيء يجب فعله هو تحديد وظيفة تأخذ ساحة اللعب كمدخلات وتُرجع الحالة التالية.
لحسن الحظ ، تتوفر العديد من التطبيقات على الإنترنت ، مثل: https://jakevdp.imtqy.com/blog/2013/08/07/conways-game-of-life/ .
في الواقع ، تأخذ مصفوفة ملعب اللعب كمدخلات ، حيث يمثل 0 خلية ميتة ، وتمثل 1 خلية حية وترجع مصفوفة من نفس الحجم ، ولكن تحتوي على حالة كل خلية في التكرار التالي للعبة.
import numpy as np def life_step(X): live_neighbors = sum(np.roll(np.roll(X, i, 0), j, 1) for i in (-1, 0, 1) for j in (-1, 0, 1) if (i != 0 or j != 0)) return (live_neighbors == 3) | (X & (live_neighbors == 2)).astype(int)
لعب جيل الميدان
باتباع منطق اللعبة ، نحتاج إلى طريقة لإنشاء حقول اللعبة بشكل عشوائي وطريقة لتصورها.
generate_frames دالة num_frames حقول اللعبة العشوائية ذات شكل معين واحتمالًا محددًا مسبقًا بأن تكون كل خلية "حية" ، render_frames للعبة جنبًا إلى جنب للمقارنة (الخلايا الحية عبارة عن خلايا بيضاء وخلايا ميتة سوداء):
import matplotlib.pyplot as plt def generate_frames(num_frames, board_shape=(100,100), prob_alive=0.15): return np.array([ np.random.choice([False, True], size=board_shape, p=[1-prob_alive, prob_alive]) for _ in range(num_frames) ]).astype(int) def render_frames(frame1, frame2): plt.subplot(1, 2, 1) plt.imshow(frame1.flatten().reshape(board_shape), cmap='gray') plt.subplot(1, 2, 2) plt.imshow(frame2.flatten().reshape(board_shape), cmap='gray')
لنرى كيف تبدو هذه الحقول:
board_shape = (20, 20) board_size = board_shape[0] * board_shape[1] probability_alive = 0.15 frames = generate_frames(10, board_shape=board_shape, prob_alive=probability_alive) print(frames.shape)
(10, 20, 20)
print(frames[0])
[[0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0], [0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1], [1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0], [1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0], [0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0], [0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0], [0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0]])
بعد ذلك ، يتم أخذ تمثيل عدد صحيح لملعب وعرضه كصورة.
يتم أيضًا عرض حالة الملعب التالية على اليمين باستخدام دالة life_step :
ender_frames(frames[1], life_step(frames[1]))

بناء التدريب واختبار مجموعات
الآن يمكننا توليد بيانات للتدريب والتحقق والاختبار.
y_train كل عنصر في y_train / y_val / y_test مجال اللعبة التالي لكل إطار في الحقل في X_train / X_val / X_test .
def reshape_input(X): return X.reshape(X.shape[0], X.shape[1], X.shape[2], 1) def generate_dataset(num_frames, board_shape, prob_alive): X = generate_frames(num_frames, board_shape=board_shape, prob_alive=prob_alive) X = reshape_input(X) y = np.array([ life_step(frame) for frame in X ]) return X, y train_size = 70000 val_size = 10000 test_size = 20000
print("Training Set:") X_train, y_train = generate_dataset(train_size, board_shape, probability_alive) print(X_train.shape) print(y_train.shape)
Training Set: (70000, 20, 20, 1) (70000, 20, 20, 1)
print("Validation Set:") X_val, y_val = generate_dataset(val_size, board_shape, probability_alive) print(X_val.shape) print(y_val.shape)
Validation Set: (10000, 20, 20, 1) (10000, 20, 20, 1)
print("Test Set:") X_test, y_test = generate_dataset(test_size, board_shape, probability_alive) print(X_test.shape) print(y_test.shape)
Test Set: (20000, 20, 20, 1) (20000, 20, 20, 1)
بناء الشبكة العصبية التلافيفية
الآن يمكننا أن نتخذ الخطوة الأولى نحو بناء شبكة عصبية تلافيفية باستخدام Keras. النقطة الأساسية هنا هي حجم النواة (3 ، 3) والخطوة 1. ويخبرون CNN باستخدام مصفوفة 3 × 3 من الخلايا المحيطة لكل خلية في الحقل الذي تبحث عنه ، بما في ذلك الخلية الحالية.
على سبيل المثال ، إذا كان الحقل التالي عبارة عن حقل لعبة ، وكنا في الخلية الوسطى x ، فستنظر في جميع الخلايا التي تحمل علامة تعجب ! والخلية
0 0 0 0 0 0! ! ! 0 0! x ! 0 0! ! ! 0 0 0 0 0 0
ما تبقى من الشبكة بسيط للغاية ، لذلك لن أخوض في التفاصيل. إذا كنت مهتمًا بأي شيء ، أوصي بقراءة الوثائق.
from keras.models import Sequential from keras.layers import Dense, Dropout, Activation, Conv2D, MaxPool2D
ألق نظرة على إخراج وظيفة summary :
model.summary()
_________________________________________________________________ Layer (type) Output Shape Param # ================================================================= conv2d_9 (Conv2D) (None, 20, 20, 50) 500 _________________________________________________________________ dense_17 (Dense) (None, 20, 20, 100) 5100 _________________________________________________________________ dense_18 (Dense) (None, 20, 20, 1) 101 _________________________________________________________________ activation_9 (Activation) (None, 20, 20, 1) 0 ================================================================= Total params: 5,701 Trainable params: 5,701 Non-trainable params: 0 _________________________________________________________________
التدريب وحفظ نموذج
بعد أن بنيت CNN ، فلنقم بتدريب النموذج وحفظه على القرص:
def train(model, X_train, y_train, X_val, y_val, batch_size=50, epochs=2, filename_suffix=''): model.fit( X_train, y_train, batch_size=batch_size, epochs=epochs, validation_data=(X_val, y_val) ) with open('cgol_cnn{}.json'.format(filename_suffix), 'w') as file: file.write(model.to_json()) model.save_weights('cgol_cnn{}.h5'.format(filename_suffix)) train(model, X_train, y_train, X_val, y_val, filename_suffix='_basic')
Train on 70000 samples, validate on 10000 samples Epoch 1/2 70000/70000 [==============================] - 27s 388us/step - loss: 0.1324 - acc: 0.9651 - val_loss: 0.0833 - val_acc: 0.9815 Epoch 2/2 70000/70000 [==============================] - 27s 383us/step - loss: 0.0819 - acc: 0.9817 - val_loss: 0.0823 - val_acc: 0.9816
يوفر هذا النموذج دقة تفوق 98٪ لكل من مجموعات التدريب والاختبار ، وهو أمر جيد جدًا للمرور الأول. دعنا نحاول معرفة أين نخطئ.
محاولة
دعونا نلقي نظرة على التوقعات الخاصة بملعب عشوائي وكيف يعمل. أولاً ، قم بإنشاء ملعب واحد وانظر إلى الإطار التالي الصحيح:
X, y = generate_dataset(1, board_shape=board_shape, prob_alive=probability_alive) render_frames(X[0].flatten().reshape(board_shape), y)

بعد ذلك ، دعونا نفعل التنبؤ ونرى عدد الخلايا التي تم التنبؤ بها بشكل غير صحيح:
pred = model.predict_classes(X) print(np.count_nonzero(pred.flatten() - y.flatten()), "incorrect cells.")
4 incorrect cells.
بعد ذلك ، دعونا نقارن الخطوة التالية الصحيحة بالخطوة المتوقعة:
render_frames(y, pred.flatten().reshape(board_shape))
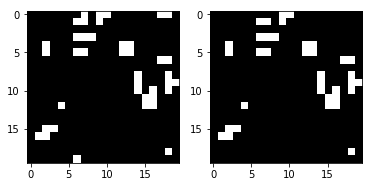
انها ليست مخيفة ، ولكن ترى أين فشل التنبؤ؟ يبدو أن الشبكة لا يمكنها التنبؤ بالخلايا على أطراف الملعب. دعنا ننظر إلى حيث تشير القيم غير الصفرية إلى تنبؤات غير صحيحة:
print(pred.flatten().reshape(board_shape) - y.flatten().reshape(board_shape))
[[ 0 0 0 0 0 0 0 -1 0 0 0 0 0 0 0 0 0 -1 -1 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 -1 0 0 0 0 0 0 0 0 0 0 0 0 0]]
كما ترون ، توجد كل القيم غير الصفرية عند حواف الملعب. دعونا نلقي نظرة على مجموعة الاختبار الكاملة ونؤكد أن هذه الملاحظة صحيحة.
عرض الأخطاء باستخدام مجموعة الاختبار
سنقوم بكتابة وظيفة تعرض خريطة حرارة توضح المكان الذي يرتكب فيه النموذج الأخطاء ، وسنسميها باستخدام مجموعة الاختبار بأكملها:
def view_prediction_errors(model, X, y): y_pred = model.predict_classes(X) sum_y_pred = np.sum(y_pred, axis=0).flatten().reshape(board_shape) sum_y = np.sum(y, axis=0).flatten().reshape(board_shape) plt.imshow(sum_y_pred - sum_y, cmap='hot', interpolation='nearest') plt.show() view_prediction_errors(model, X_test, y_test)

جميع الأخطاء عند الحواف والزوايا. هذا منطقي ، نظرًا لأن CNN لا يمكنها أن تنظر حولك ، لكن منطق اللعبة في life_step هو الذي يقوم بذلك. على سبيل المثال ، ضع في اعتبارك ما يلي. بالنظر إلى خلية الحافة x أدناه ، ترى CNN فقط x و ! الخلية:
0 0 0 0 0 ! ! 0 0 0 x ! 0 0 0 ! ! 0 0 0 0 0 0 0 0
ولكن ما نريده حقًا وما تفعله life_step هو إلقاء نظرة على الخلايا من الجانب الآخر:
0 0 0 0 0 ! ! 0 0 ! x ! 0 0 ! ! ! 0 0 ! 0 0 0 0 0
وضع مماثل في الزوايا:
x ! 0 0 ! ! ! 0 0 ! 0 0 0 0 0 0 0 0 0 0 ! 0 0 0 !
لإصلاح ذلك ، يجب على Conv2D إلقاء نظرة بطريقة ما على الجانب الآخر من الملعب. بدلاً من ذلك ، يمكن تجهيز كل حقل إدخال مسبقًا بملء الحواف على الجانب الآخر ، ومن ثم يمكن لـ Conv2D حذف العمود والصف الأول أو الأخير. نظرًا لأننا تحت رحمة Keras ووظائف التعبئة التي توفرها والتي لا تدعم ما نبحث عنه ، فسوف يتعين علينا اللجوء إلى إضافة التعبئة الخاصة بنا.
تصحيح عيوب الحافة باستخدام الملء
نحن بحاجة إلى تكملة كل حقل لعب بقيمة معاكسة لتقليد كيفية عمل life_step لقيم الحافة. يمكننا استخدام np.pad مع mode = 'wrap' لهذا الغرض. على سبيل المثال ، ضع في الاعتبار الصفيف التالي والإخراج المعزز أدناه:
x = np.array([ [1, 2, 3], [4, 5, 6], [7, 8, 9] ]) print(np.pad(x, (1, 1), mode='wrap'))
[[9, 7, 8, 9, 7], [3, 1, 2, 3, 1], [6, 4, 5, 6, 4], [9, 7, 8, 9, 7], [3, 1, 2, 3, 1]]
لاحظ أن العمود / الصف الأول والعمود / الصف الأخير يعكسان الجانب الآخر من المصفوفة الأصلية ، وأن المصفوفة 3x3 المتوسطة هي قيمة x الأصلية. على سبيل المثال ، تم نسخ الخلية [1] [1] على الجانب المقابل في الخلية [4] [1] ، وعلى نحو مشابه لـ [0] [1] تحتوي على [3] [1]. في كل الاتجاهات وحتى في الزوايا ، تم تصحيح الصفيف بحيث يحتوي على الجانب الآخر. سيسمح هذا لشبكة CNN بمراجعة ميدان اللعب بأكمله والتعامل مع الحالات القصوى بشكل صحيح.
الآن يمكننا كتابة وظيفة لملء جميع مصفوفات الإدخال لدينا:
def pad_input(X): return reshape_input(np.array([ np.pad(x.reshape(board_shape), (1,1), mode='wrap') for x in X ])) X_train_padded = pad_input(X_train) X_val_padded = pad_input(X_val) X_test_padded = pad_input(X_test) print(X_train_padded.shape) print(X_val_padded.shape) print(X_test_padded.shape)
(70000, 22, 22, 1) (10000, 22, 22, 1) (20000, 22, 22, 1)
يتم الآن استكمال جميع مجموعات البيانات بأعمدة / صفوف ملفوفة ، مما يسمح لـ CNN برؤية الجانب الآخر من الملعب ، كما هو الحال في life_step . لهذا السبب ، يبلغ حجم كل ملعب الآن 22 × 22 بدلاً من 20 × 20 الأصلي.
ثم ، يجب إعادة إنشاء CNN لتجاهل الحشو باستخدام padding = 'valid' (والذي يخبر Conv2D بتجاهل الحواف ، على الرغم من أن هذا غير واضح على الفور) ، والتعامل مع شكل إدخال جديد. وبالتالي ، عندما نتخطى ملاعب بحجم 22 × 22 ، فإننا لا نزال نحصل على حجم 20 × 20 كإخراج ، لأننا نتجاهل العمود / الصف الأول والأخير. الباقي يبقى متطابقه:
model_padded = Sequential() model_padded.add(Conv2D( filters, kernel_size, padding='valid', activation='relu', strides=strides, input_shape=(board_shape[0] + 2, board_shape[1] + 2, 1) )) model_padded.add(Dense(hidden_dims)) model_padded.add(Dense(1)) model_padded.add(Activation('sigmoid')) model_padded.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy']) model_padded.summary()
_________________________________________________________________ Layer (type) Output Shape Param # ================================================================= conv2d_10 (Conv2D) (None, 20, 20, 50) 500 _________________________________________________________________ dense_19 (Dense) (None, 20, 20, 100) 5100 _________________________________________________________________ dense_20 (Dense) (None, 20, 20, 1) 101 _________________________________________________________________ activation_10 (Activation) (None, 20, 20, 1) 0 ================================================================= Total params: 5,701 Trainable params: 5,701 Non-trainable params: 0 _________________________________________________________________
الآن يمكننا أن نتعلم باستخدام الحقل الانحياز:
train( model_padded, X_train_padded, y_train, X_val_padded, y_val, filename_suffix='_padded' )
Train on 70000 samples, validate on 10000 samples Epoch 1/2 70000/70000 [==============================] - 27s 389us/step - loss: 0.0604 - acc: 0.9807 - val_loss: 4.5475e-04 - val_acc: 1.0000 Epoch 2/2 70000/70000 [==============================] - 27s 382us/step - loss: 1.7058e-04 - acc: 1.0000 - val_loss: 5.9932e-05 - val_acc: 1.0000
دقة التنبؤ هي من 98 ٪ إلى 100 ٪ ، والتي تلقيناها قبل إضافة المسافة البادئة. دعونا نلقي نظرة على الخطأ في حالة الاختبار:
view_prediction_errors(model_padded, X_test_padded, y_test)

! ممتاز تشير خريطة الحرارة السوداء إلى عدم وجود فروق في القيم ، وهذا يعني أننا توقعنا بنجاح كل خلية لكل لعبة.
لقد كان تمرينًا صغيرًا ممتعًا للعب مع الشبكات العصبية التلافيفية دون استخدام مجموعة بيانات كبيرة. لا تتردد في التحقق من جيثب .