القبة الجيوديسية. حول الجهاز وتجربتي في العمليات الحسابية

ربما يكون من الصعب تسمية القباب الجيوديسية بشيء غير عادي أو جديد. في هذه المقالة ، سأتحدث قليلاً عن هذه التصميمات بشكل عام ، وعن بنيتها ، وأعرض أيضًا ، كمثال ، كيف فكرت في شيء حول هذا الموضوع. وسوف يكون رمز أيضا.



لن أقتبس ويكيبيديا. لماذا اخترت القبة كمنزلي؟

• مع حجم متساو ، ستكون مساحة سطح الكرة أقل من أي شكل آخر. هذا يؤثر إيجابيا على كل من استهلاك المواد واستهلاك الطاقة أثناء التشغيل.
• أنا أحب ما يشبه المجال.
• هذا مشروع هندسي مثير للاهتمام ، إلى حد ما ، يمثل تحديًا. إنه أمر صعب وصعب وبالتالي ممتع!
  

كيف يتم ترتيب هذه المجالات الجيوديسية بشكل عام؟ للوهلة الأولى ، يبدو أن هذا نوع من التشابك بين الحواف ومن الصعب اللحاق بالنظام. سنحاول معرفة ذلك.

أساس هذه الهياكل هو icosahedron أو octahedron. بشكل عام ، متعدد السطوح العادية.
في حالتي ، كان بالضبط icosahedron ويستخدم في كثير من الأحيان. بعد ذلك ، نأخذ وجهًا واحدًا ونستبدله بعدة مثلثات تتوضع رؤوسها على كرة يتزامن مركزها مع مركز المجسم الأيقوني. هذا لا يبدو جيدا جدا. دعونا استطرادا.

هناك آلة حاسبة رائعة www.acidome.ru والتي تسمح لك بتحريف مساح في الوقت الفعلي. خذ الإيكوساهيدرون كقاعدة ، اضبط التردد على 1 ، وهو جزء من الكرة 1/1.



هذا هو لدينا icosahedron الرئيسية. التكرار هو عدد الأجزاء التي سنكسرها كل حافة حافة إيكوساهيدرون. وضعنا 3.4 ، 5 ولا شيء واضح. قم بالتبديل إلى وضع السقف وابحث عن البنتاغونات. في تلك الأماكن التي نمتلك فيها الجزء العلوي من الإيكوساهيدرون - سيكون هناك البنتاغون. بين البنتاغون الثلاثة هو وجه إيكوساهيدرون.



إذا نظرت بعناية إلى الجيوديسية وتعرفت ما تبحث عنه (عادة ما يكون خماسيًا) ، يصبح انتظام الهيكل مرئيًا. على المحيط الحيوي في مونتريال ، مع بذل العناية الواجبة ، يمكنك العثور على البنتاغونات وحساب التردد. ترددنا يساوي عدد الحواف بين اثنين من البنتاغون.

مثلثات "كبيرة" نفسها ، مع رؤوس على قمم مجسم إيكولوجي ، لها هيكل أيضًا. على الأسطح الحمضية ، هذا مرئي بالألوان. توجد المثلثات بشكل متماثل فيما يتعلق بوسط المثلث "الكبير". عدد أنواعها أقل من العدد الإجمالي للمثلثات. في حالة تكرار 5 مثلثات فريدة 9.



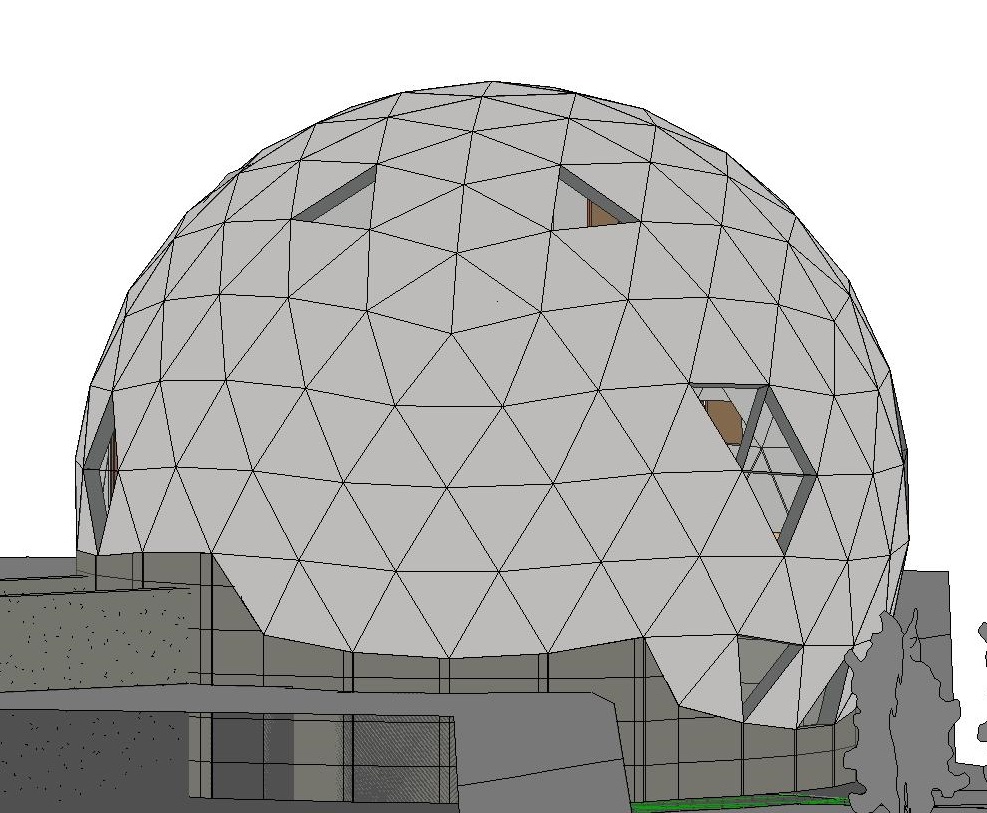
في عملية تصميم منزل ، واجهت مهمة بناء كرة في Dynamo. هذه هي الأداة التي تمكنك من تعليم Autodesk Revit للعمل مع النماذج المعقدة. مثل هذه البيئة البرمجة البصرية.
غوغلينغ ، حتى أنني وجدت رسمًا كرويًا بنى كرة أرضية في دينامو. لقد بنى الكرة ، لكن ليس ذلك.

هذا هو الشيء. عندما نأخذ إحدى حافة الإيكوساهيدرون ونقسمه إلى مثلثات صغيرة - يمكن القيام بذلك بعدة طرق. في acidome ، يكون مفتاح "طريقة التقسيم" مسؤولاً عن هذا.

قام الرسم الموجود ببناء الكرة باستخدام طريقة الوتر المتساوية. ماذا يعني هذا؟ نحن نأخذ مثلثًا كبيرًا من الإيكوساهيدرون ، ونقسم كل من حوافها إلى عدد الأجزاء التي نحتاجها ، وربط النقاط على الحواف مع بعضها البعض والحصول على شبكة مسطحة من المثلثات. ثم نعرض هذه الشبكة على الكرة. سيكون كل شيء على ما يرام ، ولكن هذه المثلثات نفسها مختلفة تمامًا في الحجم. وسط الأهم من ذلك كله. من المفهوم أن مركز المثلث "الكبير" يقع على مسافة بعيدة من المجال. هذا أمر سيء ، لأنه في هذه الحالة يكون من الأصعب تحسين استهلاك المواد. سيكون هناك المزيد من النفايات.

تفترض طريقة أخرى للتقسيم (بأقواس متساوية) أننا نبني أعلى المثلث "الكبير" للقوس ونقسمه بالفعل إلى أجزاء متساوية. النهج مختلف ، إسقاط بسيط لا يمكن القيام به.

رسم لم يصلح. حاولت إصلاحه وفي النهاية اضطررت إلى الغوص في هذا العمل برأسي.

كما اتضح فيما بعد ، بالإضافة إلى البيئة المرئية ، فإن Dynamo لديه بيثون مدمج. لم أواجه هذه اللغة من قبل ، لكن أين لم تختف لغتنا؟ في النهاية ، إنها مجرد أداة.

بعد ذلك ، سيكون هناك عدد من الكودات ، يرجى الانتباه إلى أن هذا هو عالم الترحيب الخاص بي في ثعبان ، والهدف ليس بناء الحل الأكثر فعالية وكفاءة ، ولكن بناء المجال المناسب.

طريقة أقواس متساوية.

نأخذ أحد وجوه الإيكوساهيدرون ونبني الأقواس من زوايا هذا المثلث.

for k, edge in enumerate(curves): #   arc = Arc.ByCenterPointStartPointEndPoint(sphere_center, edge.EndPoint, edge.StartPoint) #   ,    result_points.append(edge.EndPoint) result_points.append(edge.StartPoint) #    "",       if arc.SweepAngle > 90: arc = Arc.ByCenterPointStartPointEndPoint(center_point, edge.StartPoint, edge.EndPoint) #      arc_points = Arc.PointsAtEqualSegmentLength(arc, n) else: arc_points = list(reversed(Arc.PointsAtEqualSegmentLength(arc, n))) #     for p in arc_points: result_points.append(p) 

ثم نقسم الأقواس إلى أجزاء متساوية ونربط النقاط الموجودة على الأقواس بأقواس جديدة. جميع الأقواس لها مركز واحد - مركز الكرة. لا ترتبط النقاط بكل شيء ، ولكن بنفس الاسم. في الصورة يبدو أبسط مما في الكود.

 for edge_index, point_list in enumerate(points): edge_arcs = [] for point_index, point in enumerate(point_list): next_edge_index = edge_index + 1 if len(points) == next_edge_index: next_edge_index = 0 end_point_index = n - point_index - 2 arc = Arc.ByCenterPointStartPointEndPoint(center_point, points[next_edge_index][end_point_index], point) if arc.SweepAngle > 90: arc = Arc.ByCenterPointStartPointEndPoint(center_point, point, points[next_edge_index][end_point_index]) arc_points_count = n - point_index - 1; pp = Arc.PointsAtEqualSegmentLength(arc, arc_points_count) for po in pp: on_arc_points.append(po) edge_arcs.append(arc) edges_arcs.append(edge_arcs) 

عفوًا ، والأقواس لا تتقاطع! لم ينقلني غوغلينغ بطلاقة إلى كتاب أكد افتراضاتي أنه من الضروري استخدام مركز المثلث الذي يتكون من تقاطع الأقواس كأعلى حافة الجيوديسية. لقد قمت أيضًا بتدخين مصادر الحمض ، لكنني لا أتذكر إذا وجدت تأكيدًا هناك. أتذكر أنه كان مثيرا للاهتمام.
يجب أن توجد المراكز بطريقة ما. هذا هو مركز المثلث وليس من الصعب ، ولكن كان من الضروري أن نفهم أين هذه المثلثات في كومة من النقاط. بدا لي الخيار الأسهل لتوصيل النقاط الأقرب إلى بعضها البعض.

 for point in on_arc_points: distance = [] #       . for p2 in on_arc_points: distance.append(point.DistanceTo(p2)) distance.sort() #    three_points = [] for p2 in on_arc_points: if point.DistanceTo(p2) <= distance[2]: three_points.append(p2); #   poly = Polygon.ByPoints(three_points) #   .     ,    result_points.append(poly.Center()) 

الآن نحن بحاجة إلى ربط النقاط التي تم جمعها في مراحل مختلفة ، والتي هي قمم حواف الكرة الجيوديسية. في الصورة ، تكون هذه النقاط مرئية بوضوح ، ولكن عندما تكون في الصفيف - كل شيء أكثر تعقيدًا. كان هناك العديد من الخيارات ، ولكن نظرًا لأن المهمة كانت الحصول على برنامج نصي بأقل جهد ممكن ، فقد ظهر ذلك:

 #  -           ,    points = dict() for i, point in enumerate(projected): points[i] = dict() points[i]['point'] = point points[i]['id'] = i points[i]['distance'] = dict() for c, p2 in enumerate(projected): points[i]['distance'][c] = point.DistanceTo(p2) max_dist = 0 i = 0 for i, point in points.items(): max_distance = max(point['distance'].values()) if max_distance > max_dist: root_point = i max_dist = max_distance row = dict() row[root_point] = points[root_point] del points[root_point] surfaces = [] while len(row): #for x in range(0, 2): next_row = dict() for id, item in row.items(): point = closest_point(points, id) if point is not None: tmp = points[point] del points[point] point2 = closest_point(points, id) points[point] = tmp if point2 is not None: surfaces.append(Surface.ByPerimeterPoints([item['point'], points[point]['point'], points[point2]['point']])) next_row[point] = points[point] next_row[point2] = points[point2] for id, item in next_row.items(): point = closest_point(row, id) if point is not None: tmp = row[point] del row[point] point2 = closest_point(row, id) row[point] = tmp if point2 is not None: surfaces.append(Surface.ByPerimeterPoints([row[point]['point'], row[point2]['point'], item['point']])) row.clear() for id, po in next_row.items(): if po['id'] in points: del points[po['id']] if po['id'] not in row: row[po['id']] = po face_triangles = surfaces 

الجزء جاهز. ربما هناك نوع من الطريقة الصحيحة لحل هذه المشكلة ، لكنني مهدت بلدي.



ثم تتكشف القطعة ، يتم نسخها عدة مرات ، ويتم نسخها ، ويتم الحصول على كرة كاملة. هنا هو واحد من التقلبات:

 v = Vector.ByTwoPoints(sphere_center, curves[0].StartPoint) for face_triangle in face_triangles: geodesic_sphere.append(Geometry.Rotate(face_triangle, sphere_center, v, 72)) 

خرج البرنامج النصي قبيحًا ، قمت بنسخه عدة مرات ، لأنه كانت هناك مشاكل في التصدير إلى Revit. يعتقد أن هناك مشاكل مع البناء. نتيجة لذلك ، في منتدى Dynamo ، دفع الهندي الأوكراني وكان كل شيء ناجحًا!

يمكنك الآن إنشاء مجال من أي تردد وأي قطر. أظهرت مقارنة بين الأحجام والنتائج الحمضية أن كل شيء يتلاقى بدقة عالية. التكرار جيد.



لقد بدأت أيضًا في تحسين الأحجام لتقليل المحاصيل. لأن جميع الأحجام كانت في يدي ، لم يكن الأمر صعبًا للغاية. ونتيجة لذلك ، تحول نصف قطر الكرة إلى 5.65 مترًا بتردد 5. هذه الأبعاد تسمح لي باستخدام مواد بعرض 125 سم بشكل فعال ، مثل هذا العرض عبارة عن صفائح من OSB ، صفائح معدنية ، عزل ، دريوال. مع التحسين الجيد ، يكون عدد القصاصات ضئيلًا. يمكن تحقيق أفضل النتائج من خلال حساب تخطيطات المثلثات على المادة ، لكنني لم أفعل ذلك.

علاوة على ذلك ، كان الأمر أسهل ، نظرًا لأن Revit تناول شكلًا معقدًا وسمح للعمل معه بنفس النجاح تقريباً كما كان الحال مع التوازي المربعي.

بالطبع ، لم تنته الصعوبات هناك ، لكن هذه قصة مختلفة تمامًا.