مقابلة مع ويل كورت حول كتابه الجديد ، إحصائيات بايزي - إنه رائع

مرحبا يا هبر!

في نهاية العام ، نجحنا في إطلاعكم على الأخبار التي تفيد بأننا بدأنا العمل على Bayesian Statistics The Fun Way by No Starch Press. نحن نقدم ترجمة لمقابلة مفصلة مع مؤلف الكتاب ؛ يتعلق النص بكل من الكتاب نفسه والمواضيع ذات الصلة ، وحتى القراءة الإضافية.




أنا ، مثل معظم المطورين ، مهتم على الفور بالكثير من الأشياء: البرمجة الوظيفية وأنظمة التشغيل وأنظمة الأنواع والأنظمة الموزعة وعلوم البيانات. لهذا السبب ، ألهمتني معرفة أن ويل كورت ، مؤلف كتاب " الحصول على برمجة مع هاسكل" ، كتب كتابًا عن إحصائيات بايزي ، ونشرته نشرة No Starch Press. لا يوجد الكثير من الناس يكتبون كتبًا عن مواضيع مختلفة. أنا متأكد من أن لدى Will شيئًا لمشاركته مع القراء في كتابه الجديد - ولم يكن بخيبة أمل فيه. يعد الكتاب مادة تمهيدية ممتازة ، خاصة بالنسبة لأولئك الذين لا يجيدون الرياضيات القاسية ، لكنهم ما زالوا يرغبون في تحقيق شيء ما في مجال علوم البيانات. أوصي بقراءة كتاب Kurt الجديد بعد Think Stats ، ولكن قبل برمجة Python الاحتمالية: الاستدلال والخوارزميات Bayesian ، تحليل Bayesian مع Python و Doing Bayesian Data Analysis.

1. لماذا نحتاج إلى كتاب آخر عن الإحصاءات؟

تشير جميع الكتب الموجودة حاليًا حول إحصائيات بايزي إلى أن القارئ لديه بالفعل فكرة عامة عن الإحصاء وأساس متين في البرمجة. لذلك ، في الوقت الحالي ، غالبًا ما يُنظر إلى إحصائيات بايز كبديل متقدم للإحصاءات الكلاسيكية (مثل التكرار). وبالتالي ، على الرغم من تزايد إحصائيات Bayesian ، فإن المواد الموجودة عليها مصممة بشكل أساسي للأشخاص الذين لديهم بالفعل تدريب كمي جيد.

عندما يقرر الشخص "دراسة الإحصاءات" ببساطة ، فإنه يأخذ كتابًا تمهيديًا تُعرض فيه الإحصائيات من وجهة نظر متكررة ، ويقرأها ، وقد اكتشف نصفها مجموعة من الاختبارات والقواعد ، ويشعر أن هذا الموضوع بالكامل مربك للغاية. أردت أن أكتب مثل هذا الكتاب عن إحصائيات بايز بحيث يمكن لأي شخص أن يأخذها ويقرأها ، وبعد قراءتها ، يحصل على فكرة بديهية حول ماهية التفكير الإحصائي وكيفية حل المشكلات الحقيقية بمساعدة الإحصاءات. لا أرى أي سبب يجعل إحصائيات بايز لا يمكن أن تكون أول دورة تمهيدية في هذا الموضوع للمبتدئين المطلقين.

سأكون مسرورًا للغاية لو أن يومًا ما بكلمة "إحصائيات" بدأ الناس في إحصائيات بايز ، وأصبحت إحصائيات الترددات مجرد واحدة من المجالات الأكاديمية. لهذا الغرض ، هناك حاجة إلى المزيد من الكتب التي يُقترح فيها التعرف على الإحصاءات لدائرة واسعة من القراء باستخدام الأساليب البايزية ، علاوة على ذلك ، أخذ المؤلف في الحسبان أن هذا قد يكون أول من يعرف القارئ بالإحصاءات.
فكرت على الفور في تسمية هذا الكتاب "إحصائيات الطريق الممتع" ، لكنني اعتقدت أنني ربما أحصل على مجموعة من الرسائل الغاضبة من الأشخاص الذين اشتروا مثل هذا الكتاب للتحضير لامتحان القبول للإحصاءات - ووجدت الأمر مختلف تمامًا هناك! آمل أن يكون كتابي خطوة صغيرة نحو الوقت الذي سيتم فيه طلب إحصائيات بايز في اختبارات القبول ، وسيكون من المستحسن قراءة هذا الكتاب حتى بالنسبة لأولئك الذين يستعدون للامتحان.

2. ما هو الجمهور المستهدف من الكتاب؟ يمكن للشخص قراءتها دون أي خلفية رياضية؟

من خلال العمل على "إحصائيات بايز كبيرة" ، حاولت إنشاء كتاب ، من حيث المبدأ ، يمكن فهمه لأي شخص تعلم الرياضيات في نطاق برنامج المدرسة الثانوية. حتى لو كنت تتذكر بشكل غامض الجبر ، فإن سرعة العرض في كتاب ما هي التي يمكنك مواكبة ذلك. تتطلب إحصائيات Bayesian القليل جدًا من التحليل الرياضي وأكثرها تبسيطًا مع القليل من دعم كود البرنامج ، لذا أضفت تطبيقين إلى الكتاب الذي يوفر أساسيات اللغة R. هذه المادة كافية ل R لخدمتك كآلة حاسبة متقدمة ، ويتم تقديم الأفكار الأساسية للتحليل الرياضي في لدرجة أنه يمكنك معرفة جميع الأمثلة من هذا الكتاب ، حيث يتعلق الأمر بالتكاملات. ومع ذلك ، أعدك أن تقرأ الكتاب لن يكون عليك حل أي مشاكل من مجال التحليل الرياضي.

علاوة على ذلك ، بقدر ما عملت بجد ، في محاولة لتقليل مقدار المعرفة الرياضية اللازمة لقراءة كتاب ، وأنت تقرأ ، سوف تبدأ تدريجياً في تعلم طريقة التفكير الرياضية. إذا فهمت الرياضيات التي تعمل بها بشكل صحيح ، فسوف تفهمها بشكل أفضل. لذلك ، لم أحاول التهرب من الرياضيات الحقيقية ، لكنني أوضحها خطوة بخطوة ، حتى تصبح كل الرياضيات تدريجية واضحة لك. مثل الكثيرين ، اعتقدت ذات مرة أن الرياضيات هي علم معقد ، وأنه من الصعب التعامل معها. مع مرور الوقت ، أصبحت مقتنعًا أنه مع النهج الصحيح ، لا تسبب الرياضيات أي صعوبة تقريبًا. عادة ما ينشأ أي لبس في الرياضيات فقط بسبب محاولات اجتياز المادة بسرعة كبيرة - ولهذا السبب ، يتم تفويت الخطوات المهمة اللازمة للتفكير السليم.

3. لماذا يجب على مبرمج دراسة نظرية الاحتمالات والإحصاءات؟

أعتقد حقًا أنه يجب على الجميع دراسة نظرية وإحصائيات الاحتمالات إلى حد ما ، لأن هذه المعرفة ستساعد في الحكم على عدم اليقين الذي يحيط بنا في كل مكان في الحياة. بالنسبة للمبرمج ، سيتعين عليه بالتأكيد التعامل مع بعض المهام النموذجية حيث يكون من المفيد فهم الإحصاءات. من المحتمل جدًا ، في مرحلة ما من حياتك المهنية ، أن تضطر إلى كتابة رمز يتم فيه اتخاذ بعض القرارات بناءً على عوامل ضبابية مسبقة. ربما يكون هذا قياسًا لتحويل صفحة الويب ، أو توليد بعض المكافآت العشوائية في اللعبة ، أو التوزيع العشوائي للمستخدمين في مجموعات ، أو حتى قراءة المعلومات من بعض أجهزة الاستشعار الغامضة. في كل هذه الحالات ، سيساعدك فهم قوي لنظرية الاحتمالات كثيرًا. تُظهر ممارستي الخاصة أن النهج الاحتمالي يساعد كثيرًا في تصحيح العديد من الأخطاء التي يصعب إعادة إنتاجها أو تعقبها لمشكلة معقدة. إذا اتضح أن الخطأ ناتج عن عدم كفاية الذاكرة ، هل يمكنك التأكد من أن الخطأ سيحدث في كثير من الأحيان إذا تم قطع الذاكرة بشكل أصعب؟ إذا كان من الممكن شرح خلل معقد بطريقتين ، فما هي أفضل فرصة لاستكشاف أولاً؟ في كل هذه الحالات ، يمكن أن تساعد نظرية الاحتمالات. بطبيعة الحال ، فإن ذروة التعلم الآلي وعلوم البيانات تؤدي إلى حقيقة أن المهندسين يضطرون بشكل متزايد للتعامل مع المهام التي توفر فيها البرمجة العمل المباشر مع الاحتمالات.

4. هل من الممكن أن تصف باختصار الفرق بين تواتر ونهج بايزي لنظرية الاحتمالات؟

في تفسير التردد ، يتم تفسير الاحتمال على أنه بيان حول عدد المرات التي يجب أن يقع فيها الحدث أثناء المحاولات المتكررة. لذا ، عند طرح عملة معدنية مرتين ، يجب على المرء أن يتوقع أن يتم إسقاطها بحلول النسر 1 مرة ، نظرًا لأن العملة لها وجهان ، وواحد لديه نسر. في تفسير النظرية الافتراضية ، يتم تفسير الاحتمال على أنه سمة من سمات معرفتنا ، من حيث المبدأ ، باعتبارها استمرارًا للمنطق. احتمالية رمي عملة معدنية بنسر هي 0.5 ، لأنني لا أرى أي سبب وراء سقوط النسر أكثر من ذيوله. لذلك ، في حالة إرم عملة ، كلا النهجين تعمل بكامل طاقتها. ومع ذلك ، عندما يتعلق الأمر بأشياء مثل احتمالات فوز فريقك المفضل بكأس العالم ، يصبح عامل الثقة أكثر أهمية. هذا ، بالمناسبة ، يعني أيضًا أن إحصائيات Bayesian تدلي بتصريحات ليس حول العالم ، ولكن عن فهمنا للعالم. نظرًا لأن الجميع يفهمون العالم بشكل مختلف قليلاً ، فإن إحصائيات بايز تساعدنا على أخذ هذه الاختلافات في الاعتبار في تحليلنا. في نواح كثيرة ، تحليل بايزي هو علم تطور الآراء.

5. لماذا يركز الكتاب على نهج بايزي؟

هناك العديد من الأسباب الفلسفية الجيدة للتركيز على إحصائيات بايزي ، لكنني كنت مسترشداً لسبب عملي تمامًا: مع نهج بايزي ، يصبح كل شيء منطقيًا. بناءً على مجموعة صغيرة نسبيًا من القواعد البسيطة ، يمكنك تطوير حل لأي مشكلة تقريبًا قد تصادفك. هذا هو السبب في أن إحصائيات بايز قوية ومرنة للغاية ، ولهذا السبب فهي سهلة التعلم. أعتقد أن طريقة بايز في التفكير تناسب المبرمجين بالضبط. لا تحاول حل المشكلة بمساعدة اختبارات مرتجلة ، ولكنك تفكر في حلها وتدريجياً تتوصل إلى حل مبرر حقًا. من حيث المبدأ ، والإحصاءات Bayesian - وهذا هو السبب. أنت توافق على التحليل الثابت فقط إذا كان منطقيًا حقيقيًا ومُقنعًا لك ، وليس لأن اختبارك الذي يبدو تعسفيًا يمنحك قيمة لا أساس لها على قدم المساواة. بالإضافة إلى ذلك ، فإن إحصائيات Bayesian تجعل من الممكن الشك في النتيجة ومن وجهة نظر نوعية. في الممارسة اليومية ، يحدث غالبًا أن يتم عرض شخصين على نفس الحقائق ، لكن استنتاجاتهما مختلفة. تسمح لنا إحصائيات Bayesian بتصميم مثل هذا الاختلاف في الرأي رسميًا ، حتى نتمكن من التحقق من الحقائق التي نحتاج إليها حتى نغير وجهة نظرنا. لا يتعين عليك تصديق النتائج المذكورة على الورق بسبب بعض القيم p ، فأنت تصدقها ، لأنها تبدو لك مقنعة حقًا.

6. كيف ترتبط الإحصاءات البايزية بالتعلم الآلي

من بين أوجه التشابه بين التعلم الآلي (ولا سيما الشبكات العصبية) والإحصاءات البايزية التي فكرت فيها ما يلي: في كلا هذين التخصصين ، يمكن أن يكون التحليل الرياضي معقدًا للغاية. من حيث المبدأ ، التعلم الآلي هو فهم وحل المشتقات غير التافهة للغاية. يمكنك الحصول على وظيفة ، وبالتالي ، وظيفة الخسارة ، ثم (تلقائيًا) حساب المشتق ومحاولة متابعته حتى تقودك إلى المعلمات المثلى. يلاحظ العديد من الخبيثة أن الانتشار المتخلف هو مجرد "قاعدة سلسلة" ، ولكن في جميع المهام المعقدة تقريبًا المتعلقة بالتعلم الآلي ، يتم استخدامه بنجاح كبير.
إحصائيات Bayesian هي جانب آخر من جوانب التحليل الرياضي المرتبطة حل تكاملات معقدة حقا. أشار مايكل بيتانكورت ، مؤلف كتاب ستان ، تمامًا إلى أن كل التحليلات البايزية تقريبًا مرتبطة بحساب التوقعات ، أي بحساب التكاملات. نتيجة لتحليل بايزي ، لا يزال لديك توزيع خلفي ، لكن لا يمكنك استخدامه بأي شكل دون دمجه وبالتالي لا تحصل على إجابة محددة. لحسن الحظ ، لا أحد يصدر تعليقات شريرة حول التكاملات ، لأن الجميع يعلم أنه حتى أكثر العناصر تافهة معقدة للغاية. إليكم كيفية صياغة الأمثال في أحد كاريكاتير xkcd:



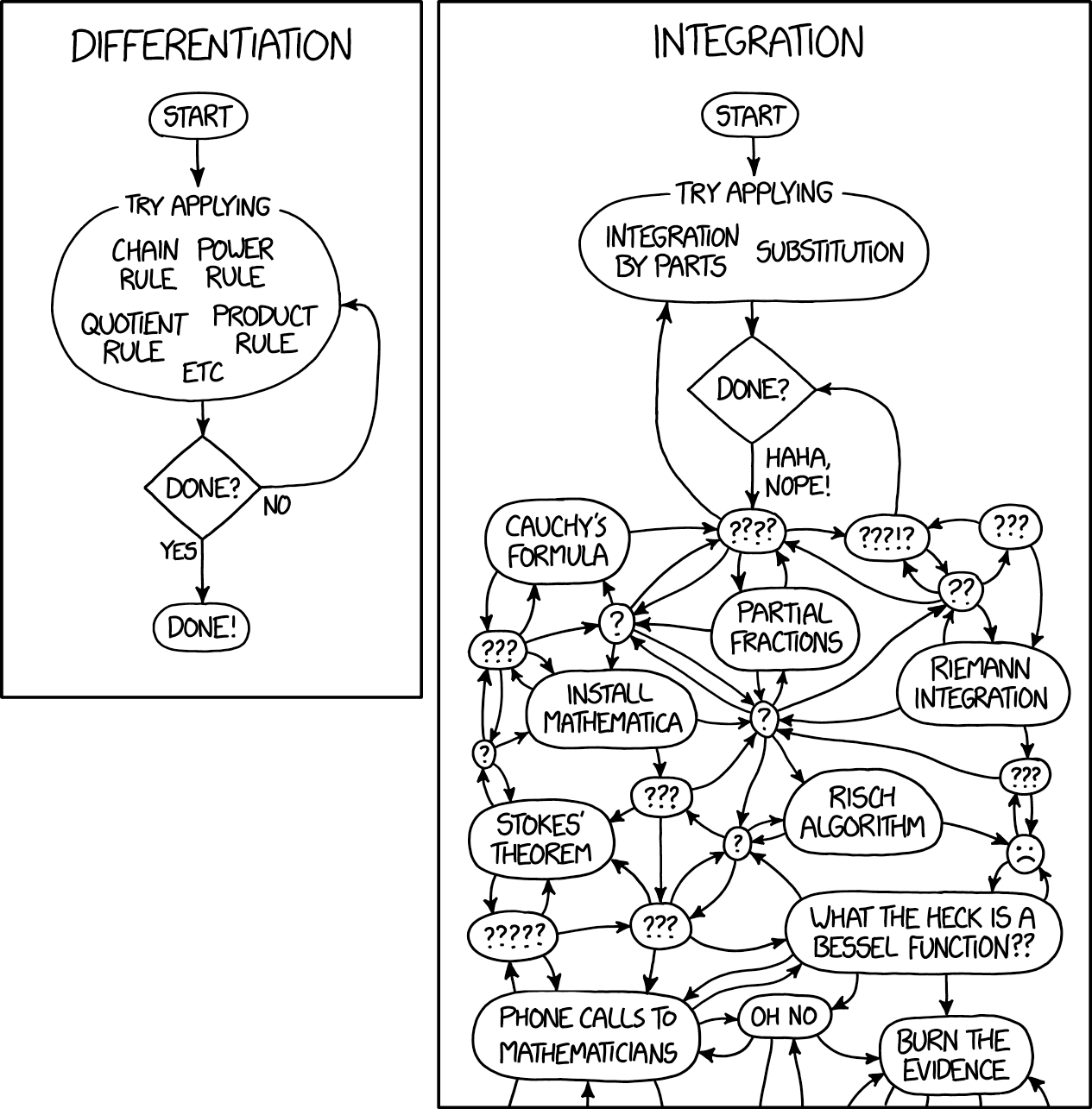
واليوم ، فإن التعليم الآلي والإحصاءات البايزية في مثل هذه الحالة الغريبة: نحن نطور أبسط أفكار التحليل الرياضي لدرجة من التعقيد لا تفسح المجال إلا للحساب.

تبرز هذه العلاقة أيضًا نقطة رئيسية واحدة. عندما نتحدث عن المشتقات ، فإننا نبحث عن نقطة محددة تتعلق بوظيفة ما. لذلك ، إذا كنت تعرف الموقف والوقت ، فإن السرعة هي أحد المشتقات التي من المفترض أن تحدد متى تسير بسرعة أكبر. هناك خطوة صغيرة نحو التقدم في MO هي عندما تكتشف أن المقياس الفردي أفضل من أي شخص آخر. التكامل هو خلاصة العملية برمتها. مرة أخرى ، إذا كنت تعرف المكان والزمان ، فإن المسافة هي المسافة البعيدة ، فهي تتيح لك معرفة المسافة التي وصلت إليها. تمثل إحصائيات Bayesian ملخصًا لكل ما تعرفه عن مشكلة ما ، لكنها لا تسمح لك بعمل توقعات منفصلة فحسب ، بل أيضًا تحديد درجة الثقة في توقعاتنا ، والتي توجد في مجموعة واسعة من الخيارات. التقدم في إحصاءات بايزي هو فهم لنظم المعلومات المتزايدة التعقيد.

7. إذا أراد القراء التعرف بشكل أعمق على موضوع الكتاب ، فما هي المواد (الكتب ، الدورات ، المدونات) التي تنصحهم بها؟

لقد استحوذت على أقصى قدر من الإلهام من كتاب I. T. Jane "نظرية الاحتمالات: منطق العلوم". سرًا ، آمل أن يصبح كتابي "إحصائيات بايزي رائعًا" نظيرًا لكتابه ، ولكنه يستهدف مجموعة واسعة من القراء. العمل مع كتاب جينس ليس بالمهمة السهلة ، فهو يمثل نتيجة جذرية للغاية لإحصاءات بايز. قام أوبري كلايتون بتقديم قدر لا بأس به من الخدمة لقرائه من خلال كتابة سلسلة من المحاضرات حول فصول هذا الكتاب.

بالطبع ، إذا كنت تحب الكتاب ، فمن المحتمل أن تحب مدونتي. في الآونة الأخيرة ، لم أكتب الكثير هناك ، لأنني كتبت كتاب "إحصائيات بايزي رائع" ، وقبل ذلك "احصل على برمجة مع هاسكل" ، لكن الآن لدي رأس مليء بالأفكار ، وليس كل منهم مكرسًا تمامًا للبيزي المواضيع. كقاعدة عامة ، أفكر في موضوع من مجال الإحصاء / الاحتمال ، ومن هذه الفكرة حددت بعناية مقالة جديدة للمدونة.

8. في تجربتك ، أي مفهوم في مجال نظرية الاحتمالات / الإحصائيات يصعب فهمه بشكل خاص؟

بصراحة ، الجزء الأصعب هو تفسير الاحتمالات. لقد فقد الناس في الواقع ثقتهم في العديد من المحللين البايزيين ، مثل Nate Silver (والعديد من الآخرين) ، عندما توقعوا أن هيلاري كلينتون ستفوز في انتخابات عام 2016 باحتمال بنسبة 80 ٪ - وفقدت. اعتقد الناس أن شخصًا ما قد خدعهم ، وكان الجميع على خطأ ، ولكن في الواقع ، فإن احتمال 80٪ ليس كثيرًا. إذا أخبرني الطبيب أن فرصي للبقاء على قيد الحياة هي 80 ٪ ، فأنا عصبي بشكل خطير.

وكقاعدة عامة ، يتم حل هذه المشكلة على النحو التالي: نشير إلى الاحتمالات على هذا النحو ونعلن أنها غير ملائمة للتعبير عن عدم اليقين. للتعامل مع هذا الإزعاج ، يجب عليك استخدام معاملات أو نسب احتمال ، أو نوع من نظام يشبه الديسيبل ، مثل مفهوم جين "للأدلة". ومع ذلك ، بعد التفكير في الاحتمالات لفترة طويلة ، توصلت إلى استنتاج مفاده أنه لا توجد وسيلة مناسبة فريدة للتعبير عن عدم اليقين.

جوهر المشكلة هو أن كل واحد منا في أعماقه مقتنع بأن هناك يقينا في العالم. حتى المتخصصين المتمرسين في نظرية الاحتمالات لديهم شعور بأنه إذا أجريت التحليل الصحيح ، واكتشف ما يلزم من بيانات مسبقة ، وأضف مستوى آخر إلى نموذجك الهرمي ، فسوف تنجح ، وستتخلص من عدم اليقين أو على الأقل تقلله . الاحتمالات جذابة بالنسبة لي جزئياً بسبب هذا المزيج الغريب من هذين العاملين: الرغبة في فهم العالم والاعتراف ، بغض النظر عن الطريقة التي تحاول بها ، أن العالم سيفاجئك على أي حال.

9. ما رأيك في القيم p كمقياس للأهمية الإحصائية؟ هل يمكن أن تصف بإيجاز ما هو القرصنة؟

في حالة القيم p ، غالباً ما يتم فهم شيئين. أولاً ، لن يحاول الشخص الذكي الإجابة عن الأسئلة ذات القيم p. تخيل كيف ستبدو المحادثة التالية في العمل:

المدير: "لقد قمت بإصلاح هذا الخطأ ، كيف تم تعيينه لك؟"
أنت: "حسنًا ، أنا أكثر من متأكد من أنني لم أصلحها ..."
المدير: "إذا قمت بإصلاحه ، فقم بتمييزه".
أنت: "أوه ، لا ، لا يمكنني القول أنني أصلحته ..."
المدير: "حسنًا ، هل ستضع علامة عليها" لن أصلحها؟ "
أنت: "لا ، لا ، بالطبع ليس الأمر كذلك على الإطلاق"

يتم الخلط بين القيم p للكثيرين لأنها غامضة بطبيعتها. تخبرك إحصائيات Bayesian بإمكانية لاحقة ، وهي إجابة إيجابية على سؤال تم وضعه كما تريد. في الحوار أعلاه ، يقول بايزي: "أنا متأكد من أنه قد تم إصلاح الخلل". إذا كان المدير يريد منك أن تستجيب بثقة أكبر ، فيمكن للبيزي جمع معلومات إضافية والقول: "أنا ، من حيث المبدأ ، أنا متأكد من أنها ثابتة".

والمشكلة الثانية هي العادة المتأصلة في اختيار 0.05 كنوع من المعنى السحري المفترض معنى. بالرجوع إلى السؤال السابق حول فهم الاحتمالات ، فإن احتمال 5٪ بحدوث حدث معين لا يعني أن هذا الحدث نادر. سيكون لديك فرصة 5 ٪ للحصول على 20 نقطة عند رمي الزهر 20 جانب. ومع ذلك ، فإن أي شخص لعب دور لعبة Dungeons و Dragons يعلم أن هذا أبعد ما يكون عن المستحيل. ما وراء آر بي جي ، رمي العظام ليس أفضل وسيلة لتمييز الحقيقة عن الأكاذيب.

هنا نأتي إلى القرصنة ع. تخيل أنك تلعب الأبراج المحصنة والتنين مع أصدقائك وتدير 20 من الزهر مرة واحدة. ثم تشير إلى النقطة التي سقطت عليها 20 نقطة ، وتعلن: "كان هذا هو العظم الذي كنت سأطرحه ، وكل الباقي كانت عبارة عن نقاط اختبار". بشكل رسمي ، لقد سجلت حقًا 20 نقطة ، ولكن هذا لا يزال عملية احتيال ، كما ترى. هذا هو جوهر القرصنة. يمكنك إجراء التحليل حتى تجد شيئًا "ضروريًا" ، ثم تدعي أن هذا هو ما كنت تبحث عنه منذ البداية.

10. التوصيات النهائية على أي كتاب لقراءة بعد لك؟

, , , , . «Bayesian Analysis with Python» (, Not Monad Tutorial). , PyMC3. , . , — “Statistical Rethinking” . , . . « – ». , «Doing Bayesian Data Analysis» .