نكتب "آلة حاسبة" في C #. الجزء الأول. حساب القيمة والمشتقات والتبسيط والأوز الأخرى

تحية!

لسبب ما ، ترتبط الحاسبة الخاصة بنا بشيء يجب على كل مبتدئ أن يكتبه. ربما لأن أجهزة الكمبيوتر تاريخيا لهذا الغرض تم إنشاؤها لحساب. لكننا سنكتب آلة حاسبة صعبة ، وليس sympy بالطبع ، ولكن لنكون قادرين على القيام بالعمليات الجبرية الأساسية ، مثل التمايز ، والبساطة ، وميزات مثل التجميع لتسريع العمليات الحسابية.


نحن نأخذ ملفات تعريف الارتباط المتبقية من العام الجديد ، وقادنا!

تجميع التعبير

ما هو التعبير؟

بالطبع ، هذا ليس خط. من الواضح أن الصيغة الرياضية هي إما شجرة أو كومة ، وهنا نتوقف عند البداية. أي أن كل عقدة ، كل عقدة من هذه الشجرة ، هي نوع من التشغيل ، متغير ، أو ثابت.



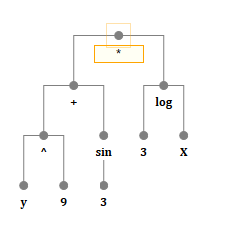
العملية إما وظيفة أو مشغل ، من حيث المبدأ ، تقريبًا نفس الشيء. أطفالها هم حجج دالة (عامل).

فئة التسلسل الهرمي في التعليمات البرمجية الخاصة بك

بالطبع ، يمكن أن يكون أي تنفيذ. ومع ذلك ، فإن الفكرة هي أنه إذا كانت الشجرة تتكون فقط من العقد والأوراق ، فستكون مختلفة. لذلك ، أنا أسمي هذه "الأشياء" - الكيانات. لذلك ، ستكون الطبقة العليا هي كيان الطبقة المجردة.


وستكون هناك أيضًا أربع فئات متتالية: NumberEntity و VariableEntity و OperatorEntity و FunctionEntity.

كيفية بناء تعبير؟

أولاً ، سنقوم ببناء تعبير في الكود ، أي

var x = new VariableEntity("x"); var expr = x * x + 3 * x + 12; 

إذا أعلنت فئة VariableEntity فارغة ، فإن مثل هذا الكود سوف يرميك خطأ ، يقولون إنهم لا يعرفون كيفية الضرب والجمع.

الغالبة مشغلي

ميزة مهمة ومفيدة للغاية لمعظم اللغات ، مما يتيح لك تخصيص تنفيذ العمليات الحسابية. يتم تنفيذه بشكل مختلف بناءً على اللغة. على سبيل المثال ، تطبيق في C #

 public static YourClass operator +(YourClass a, YourClass b) { return new YourClass(a.ToString() + b.ToString()); } 

تعرف على المزيد حول تجاوز العبارات في C #
يتم تطبيق اللفت هنا .

(غير) صب واضح

في اللغات المترجمة مثل C # ، عادة ما يكون هذا الشيء موجودًا ويسمح لك بإلقاء النوع إذا لزم الأمر دون الاتصال بـ myvar.ToAnotherType (). لذلك ، على سبيل المثال ، سيكون من المناسب الكتابة

 NumberEntity myvar = 3; 

بدلا من المعتاد

 NumberEntity myvar = new NumberEntity(3); 

المزيد عن صب النوع في C #
يتم تطبيق اللفت على هذا الخط.

تعليق

تحتوي فئة الكيان على حقل تابع - هذه مجرد قائمة بالكيان ، وهي الوسيطات لهذا الكيان.


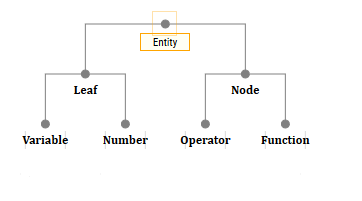
عندما نسمي وظيفة أو مشغل ، يجب أن ننشئ كيانًا جديدًا ، ونضع فيه الأطفال الذين يطلق عليهم الوظيفة أو المشغل. على سبيل المثال ، يجب أن يبدو المبلغ نظريًا كما يلي:

 public static Entity operator +(Entity a, Entity b){ var res = new OperatorEntity("+"); res.Children.Add(a); res.Children.Add(b); return res; } 

هذا هو ، الآن إذا كان لدينا كيان x وكيان 3 ، فسوف تُرجع x + 3 جوهر عامل التشغيل sum مع طفلين: 3 و x. لذلك ، يمكننا بناء الأشجار التعبير.

استدعاء الوظيفة أبسط وليست جميلة كما هو الحال مع المشغل:

 public Entity Sin(Entity a) { var res = new FunctionEntity("sin"); res.Children.Add(a); return res; } 

معلقة في اللفت تنفذ هنا .

حسنا ، لقد صنعنا شجرة تعبير.

استبدال متغير

كل شيء بسيط للغاية هنا. لدينا كيان - نتحقق مما إذا كان متغيرًا في حد ذاته ، وإذا كان الأمر كذلك ، فإننا نرجع القيمة ، وإلا فإننا نواجه الأطفال.

يقوم هذا الملف الضخم المكون من 48 سطرًا بتنفيذ مثل هذه الوظيفة المعقدة.

حساب القيمة

في الواقع ، لماذا كل هذا. من المفترض هنا إضافة نوع من الطريقة إلى الكيان

 public Entity Eval() { if (IsLeaf) { return this; } else return MathFunctions.InvokeEval(Name, Children); } 

الورقة لم تتغير ، لكن بالنسبة لكل شيء آخر ، لدينا حساب مخصص. مرة أخرى ، سأقدم مجرد مثال:

 public static Entity Eval(List<Entity> args) { MathFunctions.AssertArgs(args.Count, 1); var r = args[0].Eval(); if (r is NumberEntity) return new NumberEntity(Number.Sin((r as NumberEntity).Value)); else return r.Sin(); } 

إذا كانت الوسيطة رقمًا ، فسننتج دالة رقمية ، وإلا فإننا سنرجعها كما كانت.

العدد؟

هذا هو أبسط وحدة ، رقم. يمكن إجراء العمليات الحسابية عليها. بشكل افتراضي ، إنه معقد. لديه أيضًا عمليات مثل Sin و Cos وبعض العمليات الأخرى المحددة.

إذا كانت مهتمة ، يتم وصف الرقم هنا .

مشتق

يمكن لأي شخص حساب المشتق عدديًا ، وهذه الوظيفة مكتوبة حقًا في سطر واحد:

 public double Derivative(Func<double, double> f, double x) => (f(x + 1.0e-5) - f(x)) * 1.0e+5; 

لكن بالطبع نريد مشتقًا تحليليًا. نظرًا لأن لدينا بالفعل شجرة تعبير ، يمكننا استبدال كل عقدة بشكل متكرر وفقًا لقاعدة التمايز. يجب أن يعمل شيء مثل هذا:



هنا ، على سبيل المثال ، كيف يتم تنفيذ المبلغ في الكود الخاص بي:

 public static Entity Derive(List<Entity> args, VariableEntity variable) { MathFunctions.AssertArgs(args.Count, 2); var a = args[0]; var b = args[1]; return a.Derive(variable) + b.Derive(variable); } 

لكن العمل

 public static Entity Derive(List<Entity> args, VariableEntity variable) { MathFunctions.AssertArgs(args.Count, 2); var a = args[0]; var b = args[1]; return a.Derive(variable) * b + b.Derive(variable) * a; } 

وهنا هو الحل في حد ذاته:

 public Entity Derive(VariableEntity x) { if (IsLeaf) { if (this is VariableEntity && this.Name == x.Name) return new NumberEntity(1); else return new NumberEntity(0); } else return MathFunctions.InvokeDerive(Name, Children, x); } 

هذه هي طريقة الكيان. وكما نرى ، تحتوي الورقة على حالتين فقط - إما أنه متغير يمكننا من خلاله التمييز ، ثم مشتقها هو 1 ، أو يكون ثابتًا (رقم أو VariableEntity) ، ثم مشتقه هو 0 أو عقدة ، ثم هناك مرجع بالاسم (InvokeDerive يشير إلى قاموس الوظائف ، حيث يوجد المرغوب فيه (على سبيل المثال ، المجموع أو الجيب)).

لاحظ أنني لا أترك شيئًا مثل dy / dx هنا وأقول على الفور أن مشتق المتغير لا نفرقه هو 0. لكن هنا يتم بشكل مختلف.

يوصف كل التمايز في ملف واحد ، ولكن ليس من الضروري أكثر.

تبسيط التعبير. أنماط

تبسيط التعبير بشكل عام ليس تافهاً من حيث المبدأ. حسنًا ، على سبيل المثال ، أي التعبير أبسط: $$$x ^ 2 - y ^ 2$أو $$$(x - y) (x + y)$؟ لكننا نلتزم ببعض الأفكار ، وعلى أساسها نريد أن نجعل تلك القواعد التي تبسط التعبير بدقة.

من الممكن أن نكتب في كل Eval أنه إذا كان لدينا المبلغ ، وكان الأطفال يعملون ، فسنقوم بفرز أربعة خيارات ، وإذا كان هناك شيء متساوٍ في مكان ما ، فسنتخلص من العامل ... لكن بالطبع لا أريد القيام بذلك. لذلك ، يمكنك تخمين نظام القواعد والأنماط. إذن ماذا نريد؟ شيء مثل بناء الجملة هذا:

 { any1 / (any2 / any3) -> any1 * any3 / any2 }, { const1 * var1 + const2 * var1 -> (const1 + const2) * var1 }, { any1 + any1 * any2 -> any1 * (Num(1) + any2) }, 

فيما يلي مثال على الشجرة التي تم فيها العثور على الشجرة الفرعية (محاطة بدائرة باللون الأخضر) والتي تتطابق مع النمط any1 + const1 * any1 (any1 الموجود محاط بدائرة باللون البرتقالي).



كما ترون ، من المهم بالنسبة لنا في بعض الأحيان أن يتكرر نفس الكيان ، على سبيل المثال ، لتقصير التعبير x + a * x ، نحن بحاجة إلى أن نكون x هناك ، لأن x + a * y لم تعد مخفضة. لذلك ، نحتاج إلى عمل خوارزمية لا تتحقق فقط من تطابق الشجرة مع النمط ، ولكن أيضًا

1. تحقق من أن نمط الكيان نفسه يطابق الكيان نفسه.
2. لكتابة ما يتوافق مع ما ، ثم بديلا.

نقطة الدخول تبدو مثل هذا:

 internal Dictionary<int, Entity> EqFits(Entity tree) { var res = new Dictionary<int, Entity>(); if (!tree.PatternMakeMatch(this, res)) return null; else return res; } 

وفي tree.PaternMakeMatch ، نملأ القاموس بشكل متكرر بالمفاتيح وقيمها. فيما يلي مثال على قائمة بالكيانات ذات النمط:

 static readonly Pattern any1 = new Pattern(100, PatType.COMMON); static readonly Pattern any2 = new Pattern(101, PatType.COMMON); static readonly Pattern const1 = new Pattern(200, PatType.NUMBER); static readonly Pattern const2 = new Pattern(201, PatType.NUMBER); static readonly Pattern func1 = new Pattern(400, PatType.FUNCTION); 

عندما نكتب any1 * const1 - func1 وما إلى ذلك ، سيكون لكل عقدة رقم - هذا هو المفتاح. بمعنى آخر ، عند ملء القاموس ، ستظهر هذه الأرقام كمفاتيح: 100 ، 101 ، 200 ، 201 ، 400 ... وعند بناء شجرة ، سننظر في القيمة المقابلة للمفتاح ونستبدلها.

نفذت هنا .

تبسيط. فرز الشجرة

في المقالة التي خاطبتها بالفعل ، قرر المؤلف أن يفعل ذلك ببساطة ، وفرزها عمليًا حسب تجزئة الشجرة. تمكن من تقليل و-أ ، ب + ج + ب لتحويل 2 ب + ج. لكننا ، بالطبع ، نريد أيضًا تخفيض (x + y) + x * y - 3 * x ، وبصورة عامة الأشياء الأكثر تعقيدًا.

أنماط لا تعمل؟

بشكل عام ، ما فعلناه من قبل ، الأنماط شيء رائع بشكل فظيع. سيسمح لك بتقليل الفرق بين المربعات ، ومجموع مربع الجيب وجيب التمام ، والأشياء المعقدة الأخرى. لكن النخيل الأولي ، (((((x + 1) + 1) + 1) + 1) ، لن يقلل ، لأن القاعدة الرئيسية هنا هي تبادلية المصطلحات. لذلك ، فإن الخطوة الأولى هي عزل "الأطفال الخطيين".

"الأطفال الخطيون"

في الواقع ، لكل عقدة من المبلغ أو الفرق (وبالمناسبة ، المنتج / القسمة) ، نريد الحصول على قائمة بالمصطلحات (العوامل).



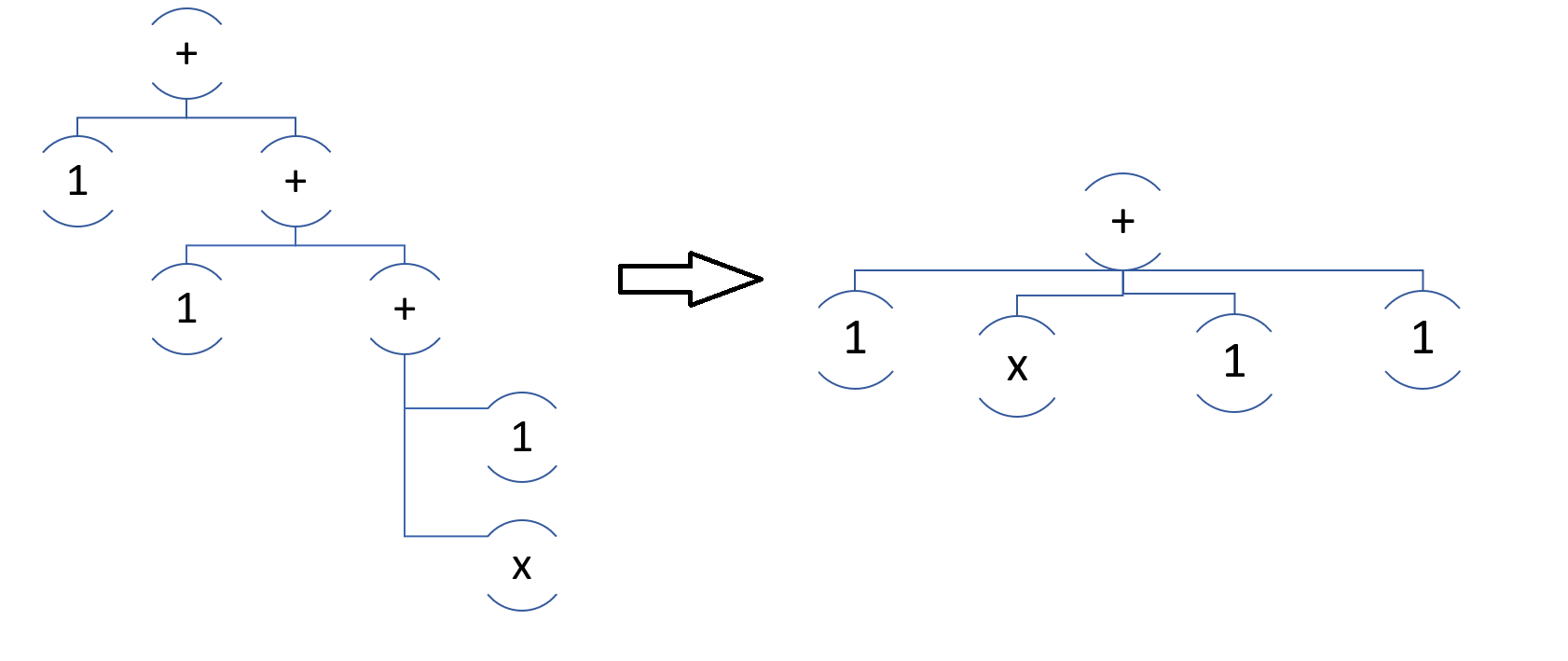
هذا واضح في الأساس. دع دالة LinearChildren (عقدة الكيان) تُرجع قائمة ، ثم ننظر إلى الطفل في العقدة. الأطفال: إذا لم يكن الطفل عبارة عن مبلغ ، فقم بنتيجة. إضافة (تابع) ، وإلا فانتيجة .AddRange (LinearChildren (تابع)).

ليست أجمل طريقة تنفذ هنا .

تجميع الأطفال

إذن لدينا قائمة بالأطفال ، لكن ماذا بعد؟ لنفترض أن لدينا خطيئة (x) + x + y + sin (x) + 2 * x. من الواضح ، ستتلقى خوارزمية لدينا خمس فصول. بعد ذلك ، نريد التجميع حسب التشابه ، على سبيل المثال ، يبدو x وكأنه 2 * x أكثر من sin (x).

هنا مجموعة جيدة:



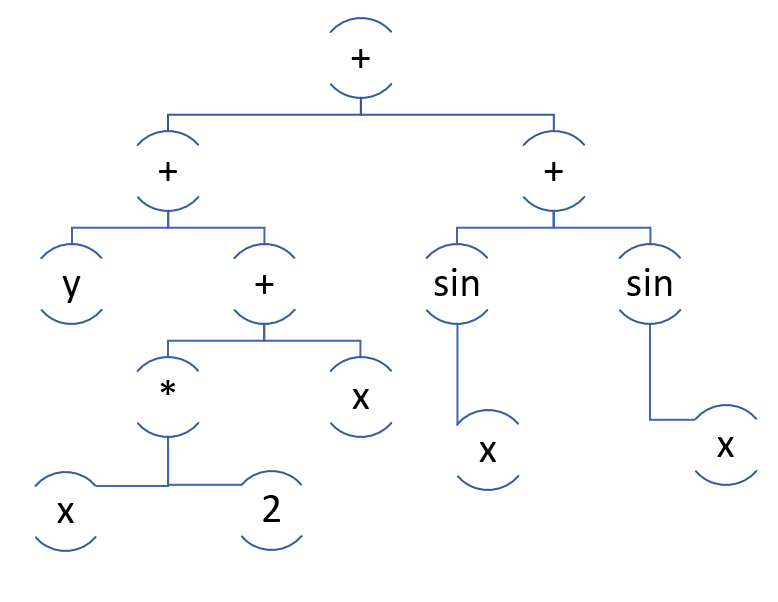
حيث أن الأنماط الموجودة فيه سوف تتأقلم أكثر مع تحويل 2 * x + x إلى 3 * x.

هذا هو ، نحن نجمع أولاً بعض العناصر ، ثم نقوم بتجميع MultiHang - تحويل مجموع n-ary إلى ثنائي.

تجزئة العقدة

من ناحية $$$x$و $$$× + 1 دولا$يجب أن توضع في مجموعة واحدة. من ناحية أخرى ، إن وجدت $$$a * x$وضعت في مجموعة واحدة مع $$$y * (x + 1)$معنى له.


لذلك ، نقوم بتنفيذ الفرز متعدد المستويات. أولاً ، نحن ندعي ذلك $$$× + 1 دولا$- نفس الشيء. مرتبة ، هدأت. ثم ندعي ذلك $$$× + 1 دولا$لا يمكن إلا أن توضع مع الآخرين $$$× + 1 دولا$. والآن لدينا $$$a * (x + 1)$و $$$y * (x + 1)$تعاونت أخيرا. نفذت بكل بساطة:

 internal string Hash(SortLevel level) { if (this is FunctionEntity) return this.Name + "_" + string.Join("_", from child in Children select child.Hash(level)); else if (this is NumberEntity) return level == SortLevel.HIGH_LEVEL ? "" : this.Name + " "; else if (this is VariableEntity) return "v_" + Name; else return (level == SortLevel.LOW_LEVEL ? this.Name + "_" : "") + string.Join("_", from child in Children where child.Hash(level) != "" select child.Hash(level)); } 

كما ترون ، تؤثر الوظيفة على الفرز بأي طريقة (بالطبع ، بسبب $$$f (x)$مع $$$x$عموما غير متصل في الحالة العامة). مثل متغير ، $$$x$مع $$$ذ$حسنًا ، لا ينجح الاختلاط. لكن الثوابت والمشغلين لا تؤخذ في الاعتبار على جميع المستويات. في هذا الترتيب ، فإن عملية التبسيط نفسها

 public Entity Simplify(int level) { //      :   ,   ,     . . var stage1 = this.InnerSimplify(); Entity res = stage1; for (int i = 0; i < level; i++) { //     .    -  x  x+1 (  ),  -  x-1  x+1 (,   ),  -  x+1  x+1 ( ). switch (i) { case 0: res = res.Sort(SortLevel.HIGH_LEVEL); break; case 2: res = res.Sort(SortLevel.MIDDLE_LEVEL); break; case 4: res = res.Sort(SortLevel.LOW_LEVEL); break; } //    . res = TreeAnalyzer.Replace(Patterns.CommonRules, res).InnerSimplify(); } return res; } 

أفرز الشجرة هنا .

"تجميع" من الوظائف

في علامات اقتباس - لأنه ليس في كود IL نفسه ، ولكن فقط في مجموعة سريعة للغاية من التعليمات. لكن الأمر بسيط للغاية.

مشكلة بديلة

لحساب قيمة دالة ، نحتاج فقط إلى استدعاء الإحلال المتغير و eval ، على سبيل المثال

 var x = MathS.Var("x"); var expr = x * x + 3; var result = expr.Substitute(x, 5).Eval(); 

لكنه يعمل ببطء ، حوالي 1.5 ميكروثانية لكل جيب.

تعليمات

لتسريع عملية الحساب ، نقوم بإجراء عملية حسابية على المكدس ، وهي:

1) لقد توصلنا إلى فئة FastExpression ، والتي ستحتوي على قائمة بالتعليمات

2) عند التجميع ، يتم تكديس التعليمات بالترتيب العكسي ، أي إذا كانت هناك دالة x * x + sin (x) + 3 ، فإن التعليمات ستكون مثل هذا:

 PUSHVAR 0 //    0 - x CALL 6 //    6 -  PUSHCONST 3 CALL 0 //    0 -  PUSHVAR 0 PUSHVAR 0 CALL 2 CALL 0 

بعد ذلك ، عند الاتصال ، نقوم بتشغيل هذه التعليمات ونعيد الرقم.

مثال على تنفيذ تعليمة المبلغ

 internal static void Sumf(Stack<Number> stack) { Number n1 = stack.Pop(); Number n2 = stack.Pop(); stack.Push(n1 + n2); } 

تم تخفيض استدعاء الجيب من 1500ns إلى 60ns (نظام Complex.Sin يعمل لمدة 30ns).
يتم تطبيق اللفت هنا .

فوه ، يبدو أن كل شيء الآن. على الرغم من أنه لا يزال هناك شيء يجب أن أخبر عنه ، إلا أنه يبدو لي أن حجم مقالة واحدة يكفي. هل هناك من يهتم بالتممة؟ وهي: تحليل من سلسلة ، والتنسيق في اللاتكس ، جزء لا يتجزأ معين ، وغيرها من الأشياء الجيدة.

ربط إلى مستودع مع كل رمز ، وكذلك الاختبارات والعينات.


شكرا لاهتمامكم!