محاكاة الجري في المطر

دخول

بدأ كل شيء ببيان استفزازي للغاية يحد من الجرأة ، والذي لا يتوافق بشكل قاطع مع فكرتي عن العالم من حولي: "يمكنك أن تبلل بدرجة أقل إذا تركضت تحت المطر - هذه خرافة". بمعنى آخر ، من هذا البيان ، يُعرف أنه من المعروف والمقبول عمومًا أن الشخص الذي يركض تحت المطر سوف يبلل أكثر من نفس الشخص الذي يمشي بنفس المسافة على الأقدام ، في نفس المطر. لكن بعض المصادر غير الموثوقة التي لم يتم التحقق منها تدعي عكس ذلك ، أنه إذا خرجت بسرعة من المطر فستصبح مبللاً بدرجة أقل.

جاء هذا البيان على البرنامج التلفزيوني Mythbusters (الحلقة 001). لقد قمت بالتدقيق مرتين عدة مرات - صياغة الأسطورة هي بالضبط: "سينتهي الأمر بالشخص أكثر جفافًا من خلال الجري في المطر بدلاً من المشي".
_{تحديث: كما اقترح rezdm هناك شريط فيديو مع صياغة مختلفة "هل يستحق تشغيل في المطر"}

علاوة على ذلك ، كانت نتيجة التحقق هي تدمير هذه الأسطورة ، أي أن القائد الذي كان يجري كان رطبًا أقوى من القائد الذي كان يمشي!؟ أي أن هذه المصادر غير الموثوقة وغير الجديرة بالثقة ، مع غباءها ، وضعت في مكانها. حتى تلك اللحظة ، كان كل شيء في العالم في الاتجاه المعاكس ، ولكي أقل بللاً ، حاولت أن أهرب إلى الملجأ.

علاوة على ذلك ، بعد عدة مواسم في وقت لاحق ، تم التحقق من هذه الأسطورة ومراجعتها (الحلقة 38). لكن النتائج في كل من الحالتين الأولى والثانية لم تكشف كثيرًا: كان الفرق في المياه التي تم جمعها ضئيلًا ، وكان بالكاد مختلفًا تمامًا عن الخطأ الإحصائي ، وعن خطأ القياس في الرصيد. في التجربة الأولى ، تم إنشاء المطر عن طريق توفير المياه إلى الرشاشات التي علقت من سقف حظيرة عالية. في التجربة الثانية ، عملوا مع ما يمكن أن يسقط من السماء. بعد التجربة الثانية ، أصبح الوضوح أقل.

لقد أحببت التجربة الأولى أكثر من ذلك ، حيث كانت هناك ظروف مسيطر عليها ، ويمكن الحفاظ على هذه الشروط في الوقت اللازم. في حالة هطول الأمطار العادية ، تتغير الظروف باستمرار - قد يتوقف المطر أو قد تتغير شدته أو تهب الرياح. في رأيي ، كان من الضروري مواصلة الدراسة الأولى: يمكنك زيادة المسافة ، ويمكن أن تلعب مع المعلمات المطر للحد من الخطأ الإحصائي وجعل النتائج أكثر إقناعا. Mythbusters هو برنامج تلفزيوني ممتاز ، لكن في هذه الحالة بالذات أردت أن أعتبره وأعيد كل شيء. مهتم بشكل خاص بموضوع تأثير طبيعة المطر على الرطب الناتج ، لأنه عادة في مثل هذه التجارب يكون متوسط ​​المطر ، وبعد كل المطر يختلف.

كما يحدث عادة ، تغلبت بشجاعة على هذه الرغبة التي لا معنى لها والتي فرضت على إعادة تجربة وأنسيتها. لكن الصيف هذا العام في منطقة موسكو بدا في كثير من الأحيان مدروسًا حول "ما إذا كان ينبغي علي الهرب من هذا المطر ، أو الذهاب بهدوء". نتيجة لذلك ، قررت أن أكتب مشروعًا صغيرًا واستكشف ما هو مثير للاهتمام بمساعدة نمذجة الكمبيوتر. كما اتضح ، في منطقة موسكو ، يبقى الموضوع ذا صلة الآن في ديسمبر.

يصف القسم التالي ما حدث ، لكنني أحتاج هنا إلى قول بضع كلمات حول تاريخ المشكلة. أثناء إعداد المقال ، اتضح أن مسألة "المشي أو الجري في المطر" كانت تطارد العديد من المهوسون حول العالم لبعض الوقت. على ما يبدو ، كانت الموجة الأولى التي صعدت هي الشهرة المعروفة للعلم ، ياكوف إيسيدوفيتش بيرلمان ، في كتابه "الميكانيكا الترفيهية" (لم ير سوى الطبعة الرابعة لعام 1937 ، لكن المهمة كانت ممكنة في المراحل السابقة التي بدأت من عام 1930) في الفصل التاسع ، "Treneye i Resistance of the Environment" " (نعم ، بداية القرن العشرين ، بعد كل شيء) يُطلق على القسم الأخير" متى ستبلل الأمطار بشكل أفضل ؟ "، لكن في الواقع ، المهمة هي" في هذه الحالة ، هل تلبس قبعتك أكثر؟ ". هناك فرق - في الكتاب الذي نتحدث فيه فقط عن عنصر المطر الذي تتصوره القبعة من الأعلى ، لا يوجد حديث عن تصادم مع المطر في المستوى الرأسي. بالإضافة إلى ذلك ، في المهمة ، يتم إجراء التجربة في نفس الوقت ، في المطر ، بينما نحن مهتمون بنفس المسافة. لا يوجد شك حول العدالة الممنوحة في كتاب القرار ، لكن اسم القسم نفسه ، والاستنتاجات المستقلة للقراء ، يمكن أن يؤدي إلى استنتاجات غير صحيحة وظهور صورة نمطية.

بعد بيرلمان كانت هناك مقالات في المجلات العلمية الشعبية من القدماء وليس ذلك ، ثم كانت هناك vidos ، والآن أصبحت الترجمة في المحور هنا . هناك مقال آخر يصعب تجاوزه وهو مقال عام 2012 للفيزيائي الإيطالي فرانكو بوكي في المجلة الأوروبية للفيزياء ، ومن غير المحتمل أن يقرأه عدد كبير من الناس ، لكن تمت كتابته في وسائل الإعلام كثيرًا ، على سبيل المثال ، تمت كتابته بشكل مثير للاهتمام ، في رأيي . هناك دراسات أخرى متفاوتة الخطورة. اتضح أن تاريخ هذه المشكلة ربما لا يقل إثارة للاهتمام عن المشكلة نفسها ، وربما يكون موضوعًا لمقال منفصل.

تصميم

القيود والافتراضات

جوهر النمذجة هو التبسيط الهادف والتجريد من إدراك الواقع. النموذج المقدم في المقال ليس استثناء. علاوة على ذلك ، قد تكون هناك دلائل تشير إلى أن ميزة معينة بسبب تفاصيل المهمة ، والقيود المادية والمعرفية ، وكذلك القيود المتعلقة بتفضيلات المؤلف الدينية أو العنصرية أو السياسية أو الجنسية وغيرها ، هي افتراض أو تقييد (بمعنى آخر ، تلك الأشياء ، والذي لم يكن كسولًا جدًا فقط ، ولكن كسولًا أيضًا لشرح السبب في أنني لم أجعلهم).

أمثلة على القيود والافتراضات: عدد القطرات في خلية واحدة (الحد الأقصى للشدة) ، جميع القطرات لها نفس الحجم ، ويفترض أن الشخص لا يلوح بالأذرع والساقين أثناء المشي والجري (تكون مناطق الإسقاط الأمامية والأفقية هي نفسها دائماً) على الظهر لا تؤخذ بعين الاعتبار ، لا توجد الرياح في التجربة ، الخ

الفضاء والرجل

الفضاء

ويمثل النموذج كائنين ، الفضاء والإنسان.

المساحة متوازية مستطيلة الشكل ، مقسمة إلى مكعبات بحجم 1x1x1 سم.

عرض المسافة يساوي عرض الشخص: في التجربة ، لا يتم اعتبار حالات الرياح والرياح الجانبية ، لذلك ، ليس من المنطقي حساب المسافة خارج عرض الشخص.

يكون ارتفاع الفضاء أكبر من ارتفاع الشخص بطبقة أفقية واحدة من المكعبات - أي سنتيمتر واحد ، في هذه الطبقة تبدأ في تسجيل القطرات ، والتي في اللحظة التالية من الوقت سوف تقع على شخص ، أو في مساحة لا يشغلها شخص آخر.

يجب أن يكون طول (مدى) الفضاء مساوياً لطول المسافة ، لكن هذا غير اقتصادي للغاية ، لأن التجربة تحتاج إلى معرفتها فقط عن حالة الفضاء فوق الشخص ، وعن عدة طبقات أمامه. لذلك ، يتم استخدام المساحة بشكل دوري في المشروع ، ويتم اختيار طوله بحيث يتم تحديث جميع الخلايا بحلول الوقت الذي يمر فيه الشخص بالكامل في الطبقة الرأسية الأولى. بمعنى آخر ، يجب أن يكون للإسقاط الذي ظهر في الطبقة خلف ظهر الشخص مباشرةً وقت كافٍ للسقوط على الأرض ، بحلول الوقت الذي يقترب فيه الشخص مرة أخرى من هذه الطبقة مع وجهه. وبالتالي ، مع التحديد الصحيح لطول المساحة ، ستنقط قطرات جديدة دائمًا على الشخص.

تجدر الإشارة إلى أنه خلال التجربة ، يتم تحديد طول المساحة مرة واحدة ، ومن ثم لا يتغير ، لذلك ، بالنسبة للإعداد الأولي للطول ، تم اختيار نسبة المعلمات بحيث يكون الطول كافياً في جميع الحالات (الحد الأقصى لسرعة الشخص والحد الأدنى لمعدل الانخفاض).

يمكن تخيل مساحة التجربة بطرق مختلفة ، على سبيل المثال ، كممر مغلق ، لكنني أفضل أن أتخيلها كنقطة مستطيلة من الضوء ، من مصباح يضيء من جانب إلى آخر ، وينتقل مع الشخص. يتم تسجيل كل قطرة تدخل الضوء داخل البقعة. يتيح لنا هذا النهج فصل مفهوم الفضاء المادي اللانهائي الذي يركض فيه شخص ما تحت المطر من مساحة التجربة - شبكة ثلاثية الأبعاد وهمية ، يتم فحص حالة كل خلية منها في كل لحظة من وقت التجربة. في المقالة ، يتم استخدام كلمة "الفضاء" في المعنى الثاني.

في البرنامج ، يتم تمثيل المساحة بمصفوفة بايت ثلاثية الأبعاد. تتوافق مؤشرات العنصر في الصفيف مع إحداثيات الخلية في الفضاء (الطول والطول والعرض) ، ويصف العنصر نفسه الحالة. يمكن أن يكون هناك حالتان فقط - هناك قطرة من المطر في الخلية أو الخلية فارغة.

يمكن أيضًا تصور الفضاء على أنه مجموعة من الطبقات الأفقية التي يسقط خلالها المطر ، وكمجموعة من الطبقات الرأسية التي يصادفها الشخص أثناء الحركة. في البرنامج ، هناك طبقات - أغلفة مسؤولة عن هذه العروض.

الناس

الشخص في المشروع هو مجرد مربع مستطيل. بالنسبة للتجربة ، نحن مهتمون في المقام الأول بإسقاطها على مستوى أفقي لحساب القطرات المتساقطة من الأعلى ، والإسقاط على مستوى عمودي متعامد مع اتجاه الحركة ، لحساب عدد النقاط التي يصادفها الشخص أثناء التقدم للأمام. يستخدم أيضا هو تنسيق المسؤول عن موقعها في الفضاء ، وعدادات المياه التي تم جمعها في المقدمة والأعلى.

من أجل تقدير مساحة الإسقاط الأفقي غوغل ، كانت واحدة من المراجع الأولى لبعض الإجراءات التنظيمية التي تستخدم وزارة الطوارئ. هناك ، يتم تمثيل الإسقاط الأفقي للشخص عن طريق القطع الناقص ذات أبعاد محورية 0.5 متر (عرض الشخص في الكتفين) و 0.25 م (سمك الشخص). يبدو أنه صحيح ، لذلك أخذت مستطيلًا من نفس المنطقة تقريبًا (S ellipse = pi * a * b S = 3.14 * (50/2) * (25/2) ~ 982 متر مربع ، مستطيل 48 في 20 = 960 سم مكعب ). كما هو موضح أعلاه ، يتم استخدام هذه البيانات ، بما في ذلك لتحديد عرض ومدى المساحة. لم أجد تعريفًا للإسقاط العمودي للشخص ، لذلك نظرًا للنمو ، فقد أخذت قيمة أقل قليلاً من المتوسط ​​- 160 سم ، والبعد الإنساني يتغير بسهولة في المشروع ، لكن التجربة أجريت على مجموعة واحدة فقط من المعلمات. نظرًا لأن هذا السؤال لم يكن مثيراً للاهتمام بالنسبة لي - أولاً ، من غير المحتمل أن تتمكن من التأثير بطريقة ما على هذه المعلمات في المطر ، وثانيًا ، أن اكتشاف اللياقة البدنية المثلى للتبلل في المطر قد يبدو مهينًا لشخص ما. أنا ربط هذا إلى القيود والافتراضات.

سرعة الإنسان: 2.196 كم / ساعة تؤخذ على أنها الحد الأدنى ؛ مأخوذة من هنا ، يبدو أن هذه البيانات تستخدم للأطراف الصناعية ، والحد الأقصى هو 43.9 كم / ساعة - أسرع سرعة تشغيل مسجلة حاليًا .

عن المطر

المطر في المشروع هو عملية تحدث في الفضاء ، ولها خصائصها الخاصة: حجم القطرة ، معدل السقوط ، الشدة.

وفقًا لـ Wikipedia ، لا يمكن أن يكون قطر قطرة المطر أقل من 0.5 مم ، لأنه لن يكون مطرًا بعد الآن ، بل رذاذ ، ولن يزيد طوله عن 6-7 مم ، في ظل هذه الظروف ، تنقسم القطرات إلى قطرات أصغر.

وفقًا لنفس المادة ، تتراوح سرعة إسقاط القطرات من 2 إلى 6 م / ث للقطرات الصغيرة ومن 9 إلى 30 م / ث للقطرات بقطر 5 مم. بحجم 5 مم إلى 7 مم ، ينخفض ​​معدل الانخفاض بسبب حقيقة أن مثل هذه القطرات الكبيرة تأخذ شكل مظلة ، ويزيد من مقاومة الهواء. يعتمد معدل إسقاط القطرات ليس فقط على حجم القطرة نفسها ، ولكن أيضًا على الظروف التي تسقط في ظلها - أفترض أن ذلك يعتمد على كثافة الهواء ، ووجود تدفقات تصاعدية أو هبوطية ، إلخ.

حدد المشروع اعتمادًا خطيًا على معدل السقوط على طول القطر: في حدود الأقطار من 0.5 إلى 5 مم ، تزداد السرعة خطيًا من 2 م / ث إلى 30 م / ث (DropSize * 6.22 - 1.11) ، في المدى من 5 مم إلى 7 مم ، تتناقص السرعة من بنفس الشدة ((10 - DropSize) * 6.22 - 1.11) ، خارج النطاق من 0.5 - 7 مم ، لم يتم إجراء التجربة.

الاعتماد الخطي المستخدم في التجربة لا يتعارض مع الصورة الحالية للعالم ، ولكنه محدود ، وبالتالي فهو افتراض. على سبيل المثال ، انخفاض قطره 5 مم في مشروع ما يتوافق مع سرعة 30 م / ث - في العالم الواقعي قد يكون هذا جيدًا (وفقًا لـ Wikipedia) ، ولكن في العالم الواقعي ، من المحتمل أيضًا أن تسقط قطرة بقطر 5 مم أبطأ بكثير - بسرعة 9 م / ث . إذا كان شخص ما مهتمًا وقرر تجربة نفسه ، فيمكنك تغيير الاعتماد على أي شخص آخر ، أو حتى تجربة العديد منها. في هذا المشروع ، سيتم استخدام هذه الميزة في كمية محدودة للغاية (بسبب ضيق الوقت).

كثافة هي سمة أخرى مثيرة للاهتمام وهامة من المطر. يشار عادة كثافة في ملليمتر في الساعة. إن ملليمتر واحد في الساعة يعني أنه خلال ساعة واحدة سوف تسقط طبقة من المياه يبلغ ملليمتر واحد على سطح أفقي من متر مربع واحد. ليس من الصعب حساب أن حجم هذه الطبقة من الماء يبلغ لتر واحد. وهذا يعني أن واحد ملم / ساعة هو نفس اللتر لكل متر مربع في ساعة واحدة. في بعض الأحيان في التنبؤات الجوية ، عندما يرغبون في وصف حجم الكارثة ، فإنها تشير ببساطة إلى ملليمترات - وهذا هو الارتفاع المحسوب لطبقة المياه التي سقطت طوال مدة المطر. في المشروع ، وكذلك في المقالة ، سيتم استخدام وحدة القياس - ملليمتر في الساعة.

وفقًا لـ Wikipedia ، عادة ما تكون شدة المطر من 0.25 مم / ساعة (أمطار متقطعة) إلى 100 مم / ساعة (مطر) - تم إجراء التجربة ضمن هذه القيم.

حول توزيع قطرات في الفضاء:

هناك نقطة واحدة مثيرة للاهتمام أود التوقف عنها لفترة وجيزة. في مرحلة التصميم ، كان من المخطط أن تملأ الطبقة الأفقية العلوية بقطرات على النحو التالي: بمجرد احتساب احتمالية حدوث قطرة تظهر في خلية ما ، وبعد ذلك ، فإن الفرز من خلال جميع خلايا الطبقة ، يقوم العشوائي ، بناءً على هذا الاحتمال ، بوضع قطرة في الخلية أم لا. تم حساب الاحتمال كنسبة عدد القطرات المطلوبة في الطبقة إلى إجمالي عدد الخلايا في الطبقة. بالنظر إلى حقيقة أن المساحة قد تقلصت بالفعل إلى الحد الأدنى ، فإن مثل هذا النهج يبدو معقولًا تمامًا. ومع ذلك ، قبل بدء التجربة ، قررت تقدير عدد القطرات لكل وحدة مساحة (نفس احتمالية الحدوث) وهذا ما حدث: فيما يلي الرسوم البيانية لعدد القطرات في طبقة بمساحة متر مربع واحد وسمك سنتيمتر واحد ، وفقًا لحجم الهبوط ، يتوافق كل رسم بياني مع شدته:

على المحور الأفقي - حجم القطرة ، على المحور العمودي - عدد القطرات. المحور الرأسي هو لوغاريتمي ، لأن الفارق في عدد القطرات كبير جدا. يفسر هذا الانتثار الكبير بحقيقة أن حجم القطرة يتناسب مع الدرجة الثالثة من أبعادها الخطية (القطر) ، بالإضافة إلى الزيادة في حجم القطرة ، يزداد معدل الانخفاض. وفقًا لذلك ، مع تغير بسيط في قطر القطرة ، يتغير عدد القطرات في الحجم كثيرًا (على سبيل المثال ، لكثافة المطر التي تبلغ 80 مم / ساعة ، ويبلغ قطر القطر 0.8 مم ، يلزم حوالي 215 قطرة لكل طبقة ، وعندما يتضاعف قطر القطرة ، يصل إلى 1.6 ملم 12 قطرات لكل طبقة).

الآن ، فيما يتعلق بالتحسين: كما يتضح من الرسوم البيانية ، حتى مع الحد الأدنى لحجم الإسقاط والحد الأقصى لشدة ، لا يتجاوز عدد القطرات لكل 10 آلاف خلية 2 × ألف ، وفي معظم الحالات يكون عدد القطرات أقل من 100 ، وإذا كان قطر القطرة أكثر من 3 مم ، فإن عدد القطرات لكل طبقة اقل من واحد وفقًا لذلك ، فإن التكرار على كل خلية من طبقات الطبقة ، بحيث لا تظهر في النهاية سوى قطرة واحدة فيها. يتمثل الخيار الأكثر اقتصادا في حساب عدد القطرات في الطبقة ، ثم يتم توزيعها بشكل عشوائي عبر الطبقة. المضاعفات الوحيدة هي الحالة عندما تكون الخلية المحددة ممتلئة بالفعل (في هذه الحالة ، العودية تبدو لطيفة). إذا أضفنا إلى هذا كله تحفيظ الخلايا المملوءة ، للتنظيف اللاحق للطبقات ، فيمكننا تحقيق وفورات كبيرة في وحدة المعالجة المركزية ، مع زيادة طفيفة في استخدام ذاكرة الوصول العشوائي.

عملية محاكاة المطر

تتم عملية وضع النماذج في دورة رئيسية واحدة. يتوافق كل تكرار لهذه الدورة مع الحد الأدنى من الفاصل الزمني (علامة). يتم تحديث كل حالة التجزئة للنظام وثابتة. تتوافق مدة علامة التجزئة مع مدة مرور قطرة المطر عبر طبقة واحدة من الفضاء (في حالتنا 1 سم) ، وبالتالي يمكن أن تتطابق علامة التجزئة في برنامج مع فترات زمنية مختلفة في الحياة الحقيقية ، اعتمادًا على معلمات الإدخال (أو بالأحرى ، على سرعة سقوط القطرات). فيما يلي وصف للإجراءات التي تحدث داخل كل تكرار:

تكون عملية المطر في المشروع كما يلي: أولاً ، يتم ملء الطبقة العلوية بشكل عشوائي مع قطرات (انظر القسم أعلاه) ، فليكن رقم الطبقة n. في التكرار التالي ، تسقط القطرات من الطبقة n في خلايا الطبقة الموجودة تحتها مباشرة - في رقم الطبقة n-1 ، يتم تعبئة الطبقة العليا مرة أخرى. علاوة على ذلك ، يحدث كل شيء بالطريقة نفسها: تقع قطرات الطبقة n-1 في الطبقة n-2 ، وقطرات n-th في الطبقة n-1 ، وتنخفض n-th مرة أخرى بشكل عشوائي ، وهكذا. عندما تصل القطرات إلى الطبقة الدنيا ، فإنها لا تفشل في أي مكان ، ولكنها تختفي ببساطة (على سبيل المثال ، تسقط على الأرض وتمتصها) ، ثم بعد التنظيف ، ترتفع هذه الطبقة ويتم إعادة استخدامها.

( ) , . , , ( ). . , , , , , ( ) , , .

, , ( ), , , , .

( ), ( ). , . , , . , . — , . , , , , . , , .

, , . , , , .

, , , .

, .

, – « , , , ?» – « ?»

. «», , , , : , ?

. « ?»

. « – , ? ?»

, . : , , , . 1 , .

, , . 2,2 /, 23,04 /, , 43,88 /. . – , .

, , . – , , , . , . , . , , . : (0.6 ), (7 ), 5 () «» (1.4 ). 10 (10 – 100 /). 1, 50 100 (, , ). . , , .

:

النتائج والاستنتاجات

, . , , 12 , 36 1 . 32 529 927 , 2 . , , , .

. , . , : « ?» : . .

, , « , ?» — , , - . :

( 20 /) 1 , 3.2 ~ 26% . , : 0,0005841873 1 1712 , 1 7,06 . – , , , , , . .

20 100 , . 23 / 43 /. , , « , ». : , , , .

, « ?».

, , :

0.6 5 , , 5 – 7 ( 7 , 5). , , .

, – , . , ( ), : , , .

– , .

, 50/ ( ). , :

, , , , .

- , . , . , , , , , , .

: « – , ? ?».

, , , , .

, :

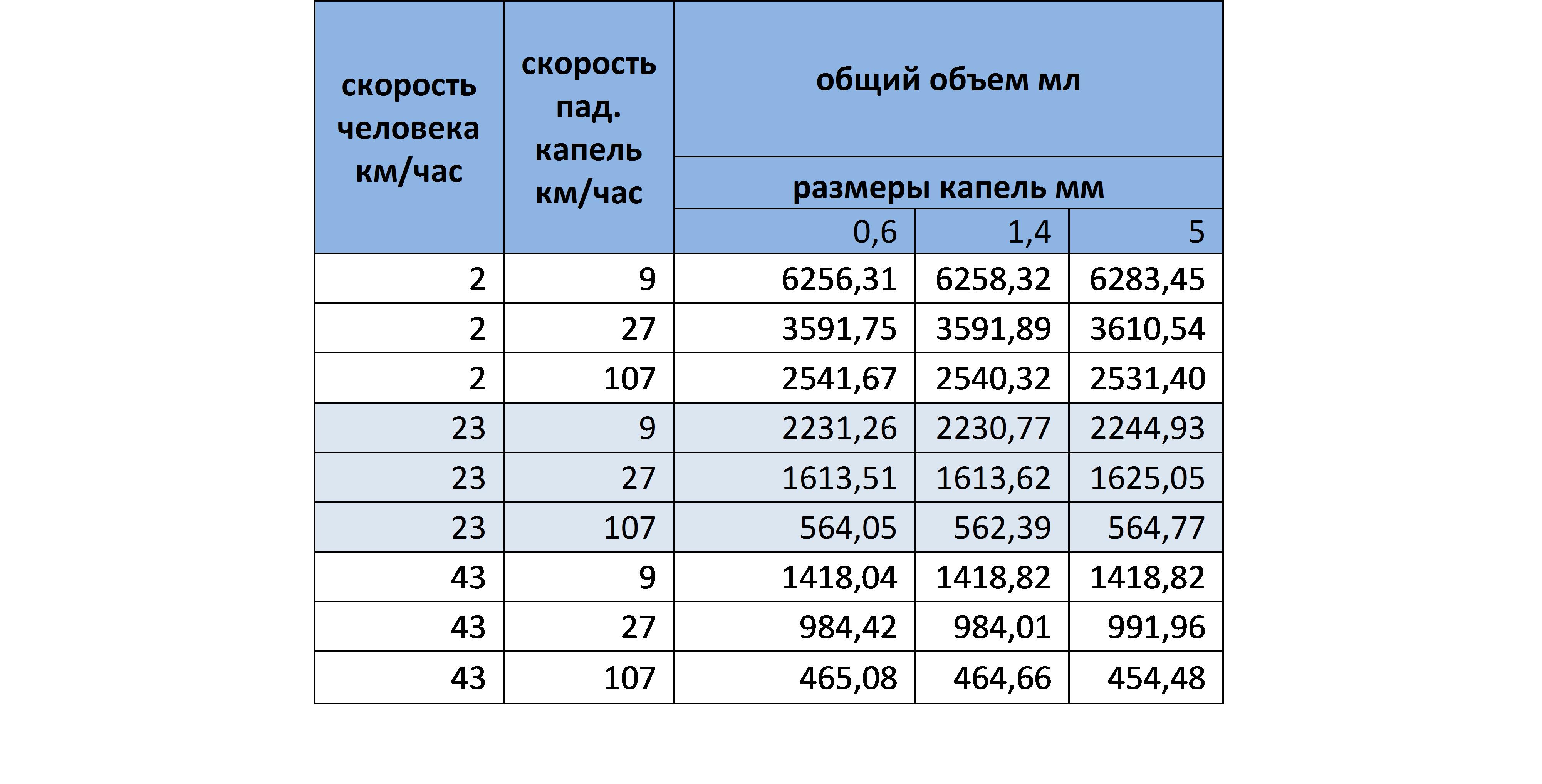
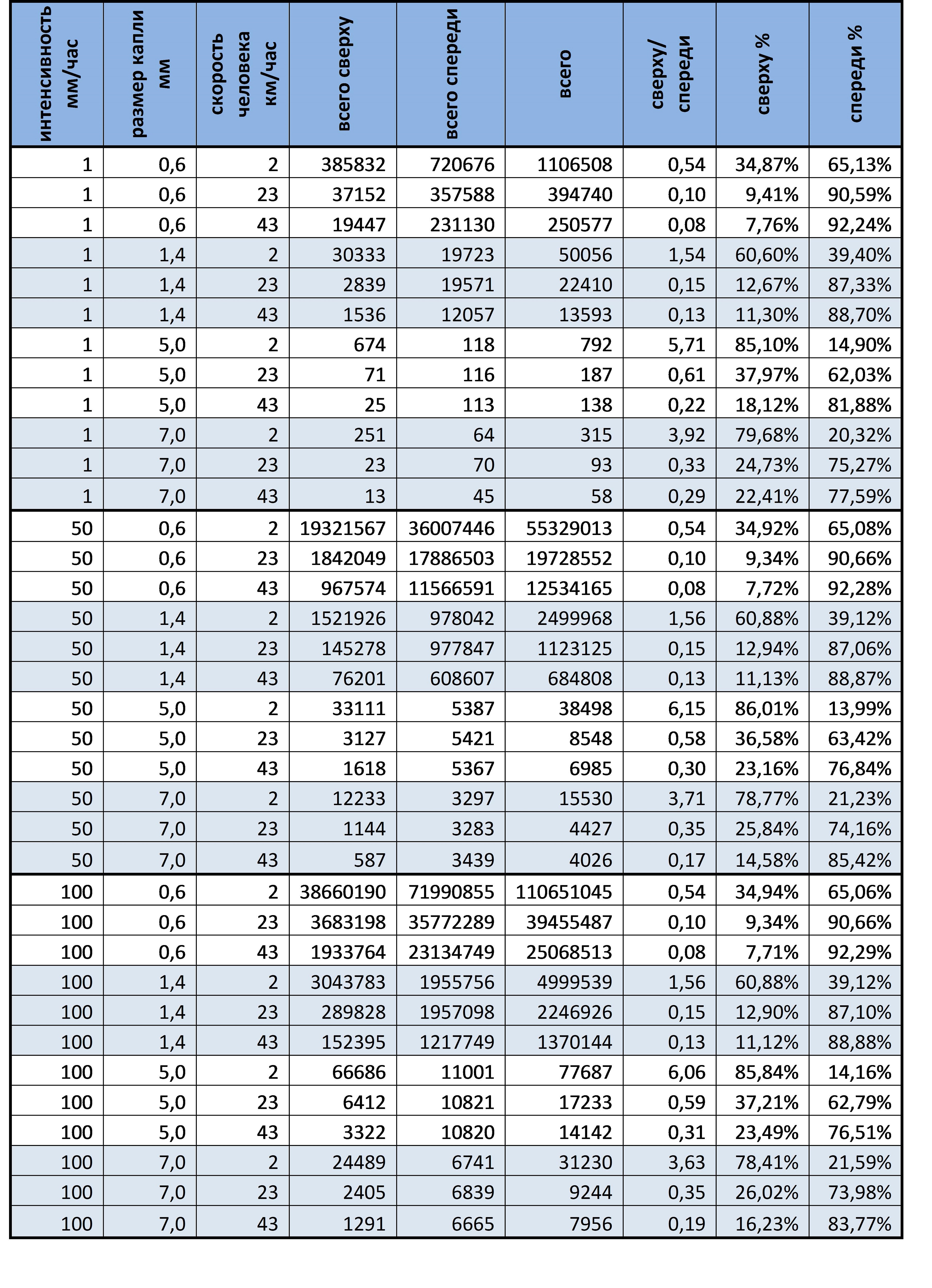
1) – , ( ).

2) , , ( 2 / 50 %).

3) , , , , ( ).

4) , . , ( ):

, , . , , , . , , , , , .

وبالتالي ، فإن الجواب على السؤال الرابع هو "على أي جانب يقوم الشخص بجمع المزيد من المياه - من أعلى أو من الجبهة؟" ما الذي تعتمد عليه هذه النسبة؟ "تقرأ: يمكن لأي شخص يمشي في المطر أن يجمع المزيد من المياه من الأعلى ومن الأمام ، وتعتمد هذه النسبة بشكل أساسي على سرعته ، ولكن سرعة قطرات القطرات لها تأثير كبير. كلما زادت سرعة الشخص ، قلت له قطرات أقل.

ربما هذا كل شيء. كما يقول الدكتور سكوت ، عالم الحفريات ، يدرس الطبيعة ويصنع اكتشافاتك الخاصة أيها الرجال. :)

ملاحظة: قد تكون هناك أخطاء في النص ، في النموذج ، في النتائج ، وفي الأسئلة المطروحة والإجابات عليها ، وفي أي أماكن أخرى ، لذلك أقوم بنشر المشروع في المجال العام إذا كان شخص ما يرغب في التحقق ، أو التحقق مرة أخرى ، أو التكرار ، أو التكميل ، أو التفكيك ، أو الوخز الأنف ، إلخ. - أرحب بكم github.com/sv-kopylov/raindrops-pub.git .

PPS هذه المقالة هي امتداد ، والآن سلسلة من المقالات حول التسلية نمذجة الكمبيوتر ، المقالة الأولى هنا.