حول بعض القضايا microoptimization

قبل التاريخ

مرة واحدة ، بدأت محادثة مع زميل حول تحسين أدوات العمل مع إشارات البت في تعدادات C ++. في ذلك الوقت ، كان لدينا بالفعل وظيفة IsEnumFlagSet ، والتي تأخذ المتغير الذي تم اختباره كوسيطة أولى والمجموعة الثانية من العلامات للتحقق. لماذا هو أفضل من القديم bitwise و؟

if (IsEnumFlagSet(state, flag)) { } // vs if (state & flag) { } 

في رأيي - سهولة القراءة. نادراً ما أتعامل مع إشارات البت وعمليات البت بشكل عام ، لذلك عند عرض رمز شخص آخر ، من الأسهل بكثير إدراك أسماء الوظائف المعتادة مقارنةً بـ cryptic & و | التي تستدعي على الفور النافذة الداخلية.alert () بعنوان "انتباه"! قد يكون هناك نوع من السحر يحدث ".


تتفاقم سهولة القراءة بشكل خاص أثناء عمليات وضع العلامات أو إزالتها. قارن:

 state |= flag; //    enum class,     |= state &= ~flag; //vs RaiseEnumFlag(state, flag); ClearEnumFlag(state, flag); 

أثناء المناقشة ، تم التعبير عن الفكرة أيضًا لإنشاء SetEnumFlag(state, flag, isSet) : اعتمادًا على الوسيطة الثالثة ، ستقوم state إما برفع علامات أو مسحها.

نظرًا لأنه كان من المفترض أن يتم تمرير هذه الوسيطة في RaiseEnumFlag/ClearEnumFlag ، فمن الواضح أنه لا يمكنك الاستغناء عن الحمل مقارنة RaiseEnumFlag/ClearEnumFlag . ولكن من أجل الاهتمام الأكاديمي ، أردت تقليله عن طريق النزول إلى المنجم إلى شيطان التحسينات الصغيرة.

تطبيق

1. تنفيذ ساذج

أولاً ، نقدم التعداد لدينا (لن نستخدم فئة التعداد لتبسيط):

 #include <limits> #include <random> enum Flags : uint32_t { One = 1u << 1, Two = 1u << 2, Three = 1u << 3, OneOrThree = One | Three, Max = 1u << 31, All = std::numeric_limits<uint32_t>::max() }; 

والتنفيذ نفسه:

 void SetFlagBranched(Flags& x, Flags y, bool cond) { if (cond) { x = Flags(x | y); } else { x = Flags(x & (~y)); } } 

2. Microoptimization

إن التطبيق الساذج له تباعد واضح ، أود نقله إلى الحساب ، والذي نحاول القيام به الآن.

أولاً ، نحتاج إلى تحديد بعض التعبيرات التي تتيح لنا التبديل من نتيجة إلى أخرى بناءً على المعلمة. على سبيل المثال

 (x | y) & ¬p 

1. عندما p = 0 نرفع الأعلام:
   
   

    (x | y) & ¬0 ≡ (x | y) & 1 ≡ x | y 

   
   
2. عند p = y تتم إزالة العلامات:
   
   

    (x | y) & ¬y ≡ (x & ¬y) | (y & ¬y) ≡ (x & ¬y) | 0 ≡ x & ¬y 

   
   

الآن نحن بحاجة إلى "حزم" بطريقة أو بأخرى في الحساب التغيير في قيمة المعلمة اعتمادًا على متغير cond (تذكر - المتفرعة محظور).

دع p = y مبدئيًا ، وإذا كان cond صحيحًا ، فحاول إعادة تعيين p ، إذا لم يكن كذلك ، فاترك كل شيء كما هو.

لن نتمكن من العمل مباشرة مع متغير cond : عند التحويل إلى النوع الحسابي ، إذا كان ذلك صحيحًا ، فإننا نحصل على وحدة واحدة فقط بالترتيب المنخفض ، ومن الناحية المثالية نحن بحاجة إلى الحصول على وحدات في جميع وحدات البت (UPD: لا يزال بإمكانك ). نتيجة لذلك ، لم يتبادر إلى الذهن أي شيء أفضل من استخدام تحولات bitwise.

نحدد مقدار التحول: لا يمكننا تحويل جميع وحدات البت لدينا على الفور حتى p إعادة تعيين المعلمة p في عملية واحدة ، لأن المعيار يتطلب أن يكون مقدار التحول أقل من حجم الكتابة.


لذلك ، نحسب الحد الأقصى لحجم التحول ، وكتابة التعبير الأولي

 constexpr auto shiftSize = sizeof(std::underlying_type_t<Flags>) * 8 - 1; (x | y) & ~ ( y >> shiftSize * cond); 

ومعالجة بشكل منفصل بت ترتيب منخفض نتيجة التعبير y >> shiftSize * cond :

 (x | y) & ~ (( y >> shiftSize * cond) & ~cond); 

تم shiftSize * cond في shiftSize * cond - وفقًا shiftSize * cond أو الحقيقي في cond ، ستكون قيمة التحول إما 0 أو 31 ، على التوالي ، وستكون المعلمة لدينا تساوي y أو 0.

ماذا يحدث عندما shiftSize = 31 :

1. مع cond = true نقوم بتحويل البتات y بمقدار 31 إلى اليمين ، ونتيجة لذلك تصبح البتة الأهم من y الأقل أهمية ، وتتم إعادة تعيين الباقي إلى صفر. في ~cond العكس ~cond ذلك ، فإن البتة الأقل دلالة هي 0 ، والباقي كلها واحدة. الضرب في هذه القيم سوف يعطي 0 نظيفة.
2. عندما يكون cond = false لا يحدث أي تحول ، في حين تحتوي ~cond في جميع الأرقام على 1 ، وسيمنح ضرب القيم في هذه القيم y .

أود أن أشير إلى المفاضلة لهذا النهج ، وهو أمر غير واضح على الفور: دون استخدام الفروع ، نحسب x | y x | y (أي ، أحد فروع الإصدار الساذج) في أي حال ، وبعد ذلك ، بسبب العمليات الحسابية "الإضافية" ، نقوم بتحويلها إلى النتيجة المرجوة. وكل هذا منطقي إذا كانت النفقات الإضافية للحساب الإضافي أقل من المتفرعة.

لذلك ، كان القرار النهائي على النحو التالي:

 void SetFlagsBranchless(Flags& x, Flags y, bool cond) { constexpr auto shiftSize = sizeof(std::underlying_type_t<Flags>) * 8 - 1; x = Flags((x | y) & ~(( y >> shiftSize * cond) & ~cond)); } 

(يكون حجم الإزاحة أكثر دقة للقراءة من خلال std::numeric_limits::digits ، راجع التعليق )

3. مقارنة

بعد أن نفذت الحل دون تفرع ، ذهبت إلى quick-bench.com للتأكد من مصلحته. من أجل التطوير ، نستخدم clang بشكل أساسي ، لذلك قررت تشغيل المعايير (clang-9.0). ولكن بعد ذلك انتظرني مفاجأة ...



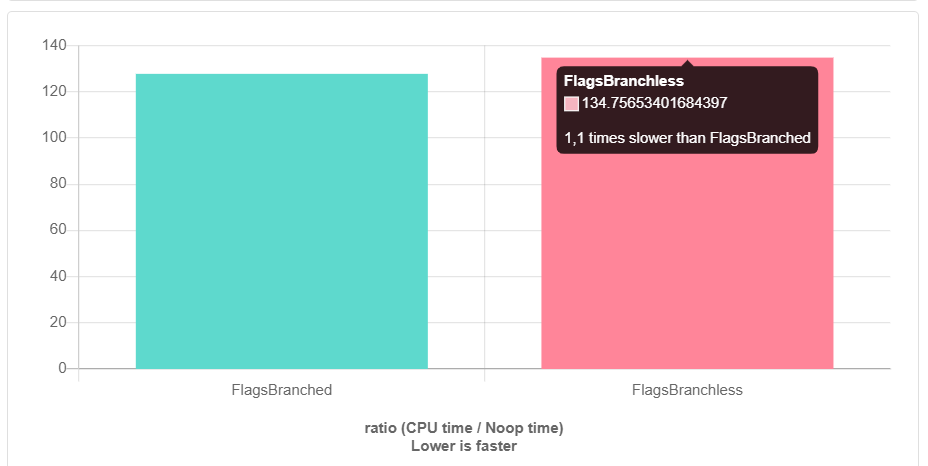
وهذا مع -O3. بدون تحسينات ، الأمر أسوأ. كيف حدث ذلك؟ على من يقع اللوم وماذا يفعل؟

نحن نأمر "نضع الذعر جانباً!" وانتقل إلى فهم godbolt.org (يوفر المقعد السريع أيضًا قائمة asm ، لكن يبدو godbolt أكثر ملاءمة في هذا الصدد).

بعد ذلك ، سنتحدث فقط عن مستوى التحسين -O3. إذن ، ما هي الشفرة التي تولدها clang لتنفيذنا الساذج؟

 SetFlagBranched(Flags&, Flags, bool): # @SetFlagBranched(Flags&, Flags, bool) mov eax, dword ptr [rdi] mov ecx, esi not ecx and ecx, eax or eax, esi test edx, edx cmove eax, ecx mov dword ptr [rdi], eax ret 

ليس سيئا ، أليس كذلك؟ يعرف Clang أيضًا كيفية المفاضلة ، ويفهم أنه سيكون من الأسرع استخدام أوامر الانتقال الشرطي لحساب كلا الفرعين واستخدام أمر النقل الشرطي ، والذي لا يتضمن تنبؤ الفرع في العمل.

كود التنفيذ بدون فروع:

 SetFlag(Flags&, Flags, bool): # @SetFlag(Flags&, Flags, bool) mov eax, dword ptr [rdi] or eax, esi test edx, edx mov ecx, 31 cmove ecx, edx shr esi, cl not esi or esi, edx and esi, eax mov dword ptr [rdi], esi ret 

"بلا فروع" تقريبًا - كما فعلت ، طلبت الضرب المعتاد هنا ، وأنت ، يا صديقي ، أحضرت خطوة مشروطة. ربما يكون المحول البرمجي صحيحًا ، وسيكون اختبار + cmove في هذه الحالة أسرع من imul ، لكنني لست جيدًا في المجمّع (الأشخاص ذوو المعرفة ، أخبرني ، من فضلك ، في التعليقات).

هناك شيء آخر مثير للاهتمام - في الواقع ، بالنسبة لكلتا العمليتين بعد التحسينات ، لم يولد المترجم ما طلبناه بالضبط ، ونتيجة لذلك حصلنا على شيء ما بين: cmove يُستخدم في كلا الخيارين ، لدينا فقط الكثير من العمليات الحسابية الإضافية في التطبيق دون الفروع ، والتي تفوق على المعيار.

يستخدم Clang من الإصدار الثامن والأقدم بشكل عام انتقالات مشروطة حقيقية ، "بسبب" يصبح الإصدار "branchless" أبطأ مرة ونصف تقريبًا:

 SetFlag(Flags&, Flags, bool): # @SetFlag(Flags&, Flags, bool) mov eax, dword ptr [rdi] or eax, esi mov cl, 31 test edx, edx jne .LBB0_2 xor ecx, ecx .LBB0_2: shr esi, cl not esi or esi, edx and eax, esi mov dword ptr [rdi], eax ret 

ما الاستنتاج الذي يمكن تحقيقه؟ بالإضافة إلى "عدم الانخراط في microoptimization الواضح دون داعٍ" ، ما لم يكن بإمكانك دائمًا النصح بالتحقق من نتيجة العمل في رمز الجهاز ، فقد يتضح أن المحول البرمجي قام بتحسين الإصدار الأولي بما فيه الكفاية بالفعل ، وأن تحسيناتك "المبدعة" لن تفهمها ، وعلى الرغم من ذلك ، فسوف تتأملها التحولات بدلا من الضرب.

في هذه المرحلة سيكون من الممكن الانتهاء ، إن لم يكن لأحد "لكن". إن رمز gcc للتطبيق الساذج مطابق لرمز clang ، ولكن النسخة بدون فروع هي::

 SetFlag(Flags&, Flags, bool): movzx edx, dl mov eax, esi or eax, DWORD PTR [rdi] mov ecx, edx sal ecx, 5 sub ecx, edx shr esi, cl not esi or esi, edx and esi, eax mov DWORD PTR [rdi], esi ret 

احترامي للمطورين لمثل هذه الطريقة الأنيقة لتحسين تعبيرنا دون استخدام إما imul أو cmove . ما يحدث هنا: يتم تبديل bit bool المتغير bwise إلى اليسار بخمسة أحرف (لأن نوع التعداد لدينا هو uint32_t ، وحجمه 32 بت ، أي 100000 ₂ ) ، ثم يتم طرحه من النتيجة. وبالتالي ، نحصل على 11111 ₂ = 31 ₁₀ في حالة cond = true ، و 0 على خلاف ذلك. وغني عن القول أن مثل هذا الخيار أسرع من الخيار الساذج ، حتى مع الأخذ في الاعتبار تحسين الحركة الشرطية؟



حسنًا ، كانت النتيجة غريبة جدًا - وفقًا للمترجم ، يمكن أن يكون الخيار بدون فروع إما أسرع أو أبطأ من التنفيذ مع الفروع. دعونا نحاول مساعدة clang وتحويل تعبيرنا باستخدام طريقة gcc (في نفس الوقت ، قم بتبسيط الجزء ~((y >> shiftSize * cond) & ~cond) وفقًا لـ de Morgan - يتم ذلك عن طريق clang و gcc):

 void SetFlagVerbose(Flags& x, Flags y, bool b) { constexpr auto shiftSize = sizeof(std::underlying_type_t<Flags>) + 1; x = Flags( (x | y) & ( ~(y >> ((b << shiftSize) - b)) | b) ); } 

مثل هذا التلميح له تأثير فقط على نسخة الجذع من clang ، حيث يُنشئ فعليًا رمزًا مشابهًا لـ gcc (على الرغم من أنه في "بلا فرع" الأصلي ، يكون نفس الاختبار + cmove)

ماذا عن MSVC؟ في كلا الإصدارين ، وبدون تشعب ، يتم استخدام imul صادق (لا أعرف مدى سرعة / أبطأ بكثير من الخيار clang / gcc - مقعد سريع لا يدعم هذا المحول البرمجي) ، وفي الوثب الساذج ظهرت قفزة مشروطة. حزين ولكن صحيح.

النتائج

ربما يمكن استنتاج أن الاستنتاج الرئيسي هو أن نوايا المبرمج في الكود العالي المستوى لا تنعكس دائمًا في كود الآلة - وهذا يجعل التقسيمات المجهرية بلا جدوى بدون علامات مرجعية وعرض القوائم. بالإضافة إلى ذلك ، يمكن أن تكون نتيجة التنبيهات المصغرة إما أفضل أو أسوأ من الإصدار المعتاد - كل هذا يتوقف على المترجم ، والذي يمكن أن يكون مشكلة خطيرة إذا كان المشروع متعدد المنصات.