n-Queens إكمال مشكلة - خوارزمية الحل الخطي

EricGrig

مقدمة

أود أن أستهل المقدمة بكلمات الشكر على اثنين من المبرمجين الرائعين من أوديسا: Andrei Kiper (Lohica) و Timur Giorgadze (Luxoft) ، للتحقق المستقل من نتائجي ، في المرحلة الأولية من الدراسة.

1. تم نشر مقالة "الخوارزمية الخطية لحل مشكلة إكمال كوينز" في (arXiv.org) في بداية اليوم الأول من عام 2020. في البداية ، تم كتابة المقال باللغة الروسية ، لذلك يتم تقديم العرض التقديمي الأساسي هنا ، وهناك الترجمة.
2. هذه المهمة ، وبعض مجموعات أخرى من مجموعات NP-Complete (مهمة إرضاء الصيغ المنطقية (3-SAT) ، مهمة العثور على الحد الأقصى للعصبة ، أو زمرة من حجم معين ...) في أوقات مختلفة ، كانت في مجال اهتماماتي. كنت أبحث عن حل حسابي يستند إلى تجارب حسابية مختلفة ، لكن لم يكن هناك نجاح ملموس. كان الأمر كما لو كان شخصًا يحاول تعلم كيفية الحصول على اللياقة على الشريط الأفقي بذراع واحدة. لا توجد نتيجة ، ولكن في كل مرة يكون هناك أمل في أن كل شيء سوف ينجح قريبًا. في آخر مرة قررت أنني يجب أن أبقى لفترة أطول في مهمة إكمال n-Queens (كأحد أفراد الأسرة) وأن أحاول القيام بشيء ما. من المناسب أن نتذكر مزحة أوديسا الرائعة: "في حافلة مزدحمة تعود إلى الضواحي على طريق وعرة في المساء ، يسمع صوت امرأة - رجل ، إذا وضعتني بالكامل ، فافعل شيئًا على الأقل."
3. استمرت الدراسة لفترة كافية - ما يقرب من عام ونصف. من ناحية ، يرجع ذلك إلى حقيقة أن المهام الأخرى قد تم النظر فيها في عملية البحث ، ومن ناحية أخرى ، كانت هناك أسئلة صعبة على طول الطريق ، والتي بدونها لم نتمكن من المضي قدمًا. سأذكر بعض منهم:
   
   
   • هناك n صفوف في مصفوفة القرار ، في أي تسلسل يجب اختيار فهرس الصف إذا كان عدد الاحتمالات لمثل هذا الاختيار هو n!
   • عند إنشاء صف ، يجب تحديد أي من المواضع الحرة المتبقية في هذا الصف ، لأن عدد الاحتمالات لهذا الاختيار كبير جدًا بحيث يمكن اعتباره "قريبًا قريبًا" من اللانهاية (على سبيل المثال ، عدد الطرق الممكنة لتحديد موضع مجاني في جميع الصفوف للرقعة بحجم 100 × 100 تقريبًا 10 ¹²⁴
   • معا ، يشكل هذان المؤشران فضاء دولة (مساحة اختيار). يبدو أن هناك فرصا هائلة ، يمكنك اختيار ما تريد. ولكن وراء كل اختيار معين في كل خطوة ، هناك مشكلة أخرى - الحد من الاختيار في جميع الخطوات اللاحقة. علاوة على ذلك ، هذا أمر حساس بشكل خاص في المراحل الأخيرة من حل المشكلة. يمكننا أن نقول أن مصفوفة القرار هي "انتقامية". جميع "الأخطاء اللاواعية" التي ترتكبها عند اتخاذ خيار في المراحل السابقة يتم "تجميعها" ، وفي نهاية القرار يتجلى ذلك في حقيقة أنه في تلك السطور التي يجب أن تضع فيها الملكة ، لا توجد مواقف فارغة ويتوقف فرع البحث عن التوقف . هنا ، كما هو الحال مع Zhvanetsky: "خطوة واحدة خاطئة ، وأنت حامل".
   • عندما يصل فرع البحث عن حل إلى طريق مسدود ، تتاح لنا الفرصة للعودة إلى بعض المواضع السابقة (تتبع التعقب) ، حتى نبدأ من هذا الموضع من جديد تشكيل فرع البحث عن حل. هذه "خاصية" طبيعية للمشاكل غير الحتمية. السؤال هو أي من المستويات السابقة يجب أن تعاد. هذه هي نفس المشكلة المفتوحة مثل مسألة اختيار فهرس الصف ، أو اختيار موضع مجاني في هذا الصف.
   • أخيرًا ، يجب ملاحظة مشكلة تتعلق بسرعة الخوارزمية. سيكون من المحزن إذا لم يكن هناك هدف لإنشاء خوارزميات سريعة الجري. في عملية النمذجة ، لم يكن من الممكن تطوير خوارزمية واحدة تعمل بسرعة وكفاءة في جميع مجالات حل المشكلة. اضطررت لتطوير ثلاث خوارزميات. أنها تنقل النتائج واحدة إلى أخرى ، مثل عصا. واحد منهم يعمل بسرعة كبيرة ، ولكن بوقاحة ، والآخر - على العكس من ذلك ، يعمل ببطء ولكن بكفاءة. كل واحد منهم يعمل في "منطقة مسؤوليتهم".
4. في البداية ، كان الغرض من الدراسة هو إيجاد حل على الأقل. كان لدي الكثير لمعرفة قبل تطوير الحل الأول. استغرق الأمر أكثر من أربعة أشهر. كان من الممكن التوقف عند هذا الحد ، لقد تحقق الهدف - حسنًا ، حسنًا. ولكن يبدو لي أنه لم يتم استنفاد جميع إمكانيات حل حسابي لهذه المشكلة. وبطبيعة الحال ، كانت هناك رغبة في تحسين الخوارزمية المتقدمة بحيث يكون التعقيد الزمني للخوارزمية خطي- O (n). عندما تم العثور على مثل هذا الحل الخطي ، كانت هناك "رغبة واحدة أخرى" - لتقليل عدد الحالات عند استخدام إجراء تتبع المسار (BT) في تكوين فرع البحث عن الحلول. لقد كانت رغبة "وقحة" في نقل المهمة من غير حتمية إلى تحديد مشروط (إلى أقصى حد ممكن). استغرق الأمر الكثير من الوقت ، ولكن تم تحقيق الهدف ، على سبيل المثال ، في الفاصل الزمني لقيم حجم رقعة الشطرنج n = (320 ، ... ، 22500) ، فإن عدد الحالات التي لم يتم فيها استخدام إجراء BT هو أكثر من 50٪. اتضح أنه في 50٪ من الحالات عندما يتم إطلاق البرنامج ، تشكل الخوارزمية "بشكل هادف" حلاً ، ولا "تتعثر" أبدًا. (تذكر حكاية خرافية عن ذهبية ، توقفت عن هذه الرغبات اثنين ...)
5. بمقارنة المنشورات التي تمكنت من التعرف عليها أثناء البحث ، توصلت إلى استنتاج مفاده أن هذه المشكلة وغيرها من المشاكل من هذا النوع لا يمكن حلها على أساس نهج رياضي صارم ، أي فقط على أساس التعاريف وبيان lemmas وإثبات النظريات. هناك "ملاحظة فلسفية" حول هذا الموضوع في المقال. أنا متأكد من أن العديد من المشكلات من NP-Complete يمكن حلها فقط على أساس الرياضيات الحسابية باستخدام نماذج الكمبيوتر. مثل هذا الاستنتاج لا يعني الحد من الرياضيات ، بل على العكس من ذلك ، فهو يعني توسيع قدرات الرياضيات من خلال تطوير أساليب الرياضيات الحسابية. لكل عائلة من المشاكل تحتاج إلى استخدام النهج الرياضي الخاص بك. (لماذا يجب تعيين طالب دراسات عليا لحل مشكلة من عائلة NP-Complete دون تطبيق أساليب حسابية في الرياضيات ونمذجة الكمبيوتر ، إذا كان من المعروف أنه لن يحدث شيء من هذا القبيل في الواقع).
6. أي خوارزمية (برنامج) لديه خاصية بسيطة - إما أنها تعمل أم لا! أريد أن أناشد أعضاء Habro-Community الذين لديهم جهاز كمبيوتر مثبت عليه Matlab في منطقة الوصول. أريد أن أطلب منك اختبار تشغيل الخوارزمية المدروسة لحل مشكلة إكمال n-Queens . هذا سيستغرق 5-10 دقائق فقط. لاختبار الخوارزمية ، تحتاج إلى اتباع بعض الخطوات البسيطة:
   
   
   • توليد تكوين عشوائي من الملكات k والتحقق من صحة هذا التكوين.
   • بناءً على خوارزمية القرار المقترحة ، أكمل هذا التكوين إلى حل كامل. أو يجب أن يقرر البرنامج أن هذا التكوين لا يوجد لديه حل.
   • تحقق من صحة الحل الذي تم الحصول عليه نتيجة التكوين.
   
   
   ليس لديك لكتابة أي رمز لمثل هذا الاختبار. بالإضافة إلى البرنامج الرئيسي ، قمت بإعداد برنامجين آخرين بلغة ماتلاب:
   
   1. Generarion_k_Queens_Composition - إنشاء تكوين عشوائي من الحجم k للرقعة التعسفية بحجم nxn
   
   2. complet_k_Queens_Composition.m - إكمال التكوين التعسفي حتى اتخاذ قرار كامل ، أو تقرير أن هذا التكوين لا يوجد لديه حل ( البرنامج الرئيسي ).
   
   3. Validation_n_Queens_Solution.m - التحقق من صحة حل مشكلة n-Queens ، أو صحة تكوين k quen.
   
   انهم يعملون بسرعة كبيرة. على سبيل المثال ، بالنسبة إلى رقعة الشطرنج بحجم 1000 × 1000 خلية ، إجمالي الوقت الذي يستغرقه في المتوسط ​​لإنشاء تكوين تعسفي (0.0015 ثانية.) ، أكمل هذا التكوين (0.0622 ثانية) ، وتحقق من صحة الحل الذي تم الحصول عليه (0.0003 ثانية). لا يتجاوز 0.1 ثانية. (باستثناء الوقت الذي يستغرقه تنزيل البيانات أو حفظ النتائج)
   
   أرسل لي رسالة بالبريد الإلكتروني (ericgrig@gmail.com) ، إذا كانت لديك الفرصة لمساعدة صديق ، فسوف أرسل لك على الفور هذه البرامج الثلاثة. سأكون ممتنًا لجميع زملائي الذين يمكنهم اختبار الخوارزمية بشكل موضوعي والتعبير عن رأيهم في المناقشة.
7. أعددت شفرة المصدر للبرنامج ، مع تعليقات مفصلة ، والتي آمل أن يتم نشرها على حبري قريبًا. أعتقد أن أولئك الذين يرغبون في حل المشكلات المعقدة من عائلة NP-Complete سيجدون شيئًا مثيرًا للاهتمام لأنفسهم.
8. أود أن أناشد مرة أخرى أعضاء مجتمع هبر ، لكن لسبب مختلف. هنا ، في مرسيليا (فرنسا) ، لا يزال تشكيل فريق France Fold Group مستمرًا ، والغرض منه هو البحث وتطوير الخوارزميات للتنبؤ بالخصائص الفيزيائية والكيميائية لمركبات الوزن الجزيئي العالي. أعتقد أنه لا يستحق القول إن هذه مهمة صعبة إلى حد ما ، ولها تاريخ طويل ، وأن الفرق الجادة في مختلف البلدان تعمل على هذه المشكلة ، بما في ذلك فريق خصب من Deep Mind (يمكنك الاطلاع على مقالة عن Habré (habr.com_Folding) . الهدف هو إنشاء فريق قوي لا يخاف من حل المشكلات المعقدة ، ويتم توزيع شكل تنظيم العمل المشترك ، حيث يعيش كل عضو في الفريق في مدينته ويعمل في المشروع في وقت فراغه من عمله الرئيسي ، ونحن بحاجة إلى المبرمجين والباحثين (الفيزيائيين والكيميائيين والرياضيين وعلماء الأحياء) ) ، الخ osto "المتهور" المبرمجين (تربيع). اكتب لي إذا وجدت أنها مثيرة للاهتمام ، ما سبق هو البريد الإلكتروني الخاص بي. بمزيد من التفاصيل أستطيع أن أقول في خطاب الاستجابة.

تحولت مقدمة المقال إلى ما دامت المقالة نفسها. يسمح لي تنسيق العرض التقديمي للعائلة على Habré بالتعبير عن أفكاري بحرية أكبر ، لكن من خلال الحجم ، استفدت منه بحرية تامة. أردت أن أكتب لفترة وجيزة ، ولكن "اتضح كما هو الحال دائمًا".

ملحوظة: اعتقدت أن أعضاء مجتمع هبر مهتمون بمعرفة الصعوبات التي واجهتها عند محاولة نشر نتائج الدراسة. عندما أعد المقال ، أعدت تنسيقه إلى صيغة. tex وفقًا لمتطلبات مجلة أبحاث الذكاء الاصطناعي (JAIR) وأرسلته إلى هناك. اعتادت ان تكون هناك منشورات عن موضوع مشابه. من الجدير بالذكر هو المادة ج. جنت ، I.-P. Jefferson and P. Nightingale (2017) (تعقيد إكمال ملكات n) ، حيث أثبت المؤلفون أن المشكلة المعنية تخص مجموعة NP-Complete وتحدثوا عن الصعوبات التي صودفت في محاولة حل هذه المشكلة. في الخلاصة ، يكتب المؤلفون: "بالنسبة لأي شخص يفهم قواعد الشطرنج ، قد يكون إكمال n-Queens أحد أكثر مشكلات NP-Complete الطبيعية على الإطلاق" ( بالنسبة لكل من يفهم قواعد الشطرنج ، يمكن أن تصبح مهمة n-Queens إكمال واحدة من المهام الأكثر طبيعية NP- كاملة ).

بعد 10 أيام ، تلقيت رفضًا من JAIR ، حيث صيغت العبارة: "لا يتوافق المقال مع نسق المجلة" ، أي لم تأخذ حتى المادة للنظر فيها. لم أكن أتوقع مثل هذه الإجابة. اعتقدت أنه إذا نشرت إحدى المقالات مقالات خلص فيها المؤلفون إلى أنه من الصعب للغاية حل مشكلة معينة ولا توفر أي حل ملموس ، فسيتم بالتأكيد قبول المقالة التي توفر خوارزمية حل فعال للنظر فيها. ومع ذلك ، كان للمحررين رأيهم الخاص في هذا الشأن. (أعتقد أن المتخصصين الأكفاء يعملون هناك ، وعلى الأرجح قد تم استجوابهم من خلال عنوان المقالة "الوقح" وكل ما هو مذكور هناك. ظننا أن "هناك على الأرجح نوعًا ما من الخطأ وأرسلتني بعيدًا ، مشيرًا إلى التنسيق ").

اضطررت إلى اختيار منشور علمي دوري آخر راجعه النظراء حول الموضوعات ذات الصلة. أنا هنا أواجه حقيقة قاسية. والحقيقة هي أن ما يقرب من 80 ٪ من جميع المجلات يتم دفعها: إما أن أدفع مبلغًا جيدًا للمجلة بحيث تكون المقالة متاحة مجانًا لجميع القراء ، أو يحتاجون إلى تقديم المقال كهدية "في القوس" ، وسيتقاضون أي شخص يريد التعرف على هذه الدراسة. والخياران الأول والثاني غير مقبولين بالنسبة لي. شعرت بالرضا تجاه طريقة مضرب الناشر هذه عندما حاولت التعرف على بعض المنشورات.

المجلة التالية ، التي تقر بمبدأ الوصول الحر إلى المعلومات ، هي مجلة SMAI Journal للرياضيات الحاسوبية . رفضوا أيضًا بالصياغة نفسها ، رغم أنها أسرع بكثير - خلال يومين.

ثم تم اختيار مجلة: الرياضيات المنفصلة وعلوم الكمبيوتر النظرية . المتطلبات بسيطة هنا ، تحتاج أولاً إلى نشر المقالة في arXiv.org ، وفقط بعد ذلك سجل المقال للنظر فيه. حسنًا ، سوف نتبع القواعد - قدمت مقالة في arXiv.org . لقد كتبوا لي أنهم سينشرون المقال في غضون 8 ساعات. ومع ذلك ، لم يحدث هذا بعد 8 ساعات ، وليس بعد 8 أيام. كان المقال "محتجزًا" من قبل الموجهين ، ولم يتم نشره إلا بعد 9 أيام. لم تكن هناك شكاوى في شكل وجوهر المقال. أعتقد ، كما في حالة JAIR ، كان لدى الموجهين شكوك حول إمكانية "القيام بذلك والكتابة عنه". بعد مرور بعض الوقت ، بعد تصحيح الأخطاء الفنية ، تم تحديث المقالة وتم إصدارها بشكلها النهائي في ليلة رأس السنة.

لا بد لي من الخوض في هذا بالتفصيل لإظهار أنه في مرحلة نشر نتائج البحوث قد تكون هناك مشاكل لا يمكن تفسيرها منطقيا.

فيما يلي مقال نُشرت ترجمته إلى الإنجليزية في (arXiv.org) .

1. مقدمة

من بين الخيارات المختلفة لصياغة مشكلة n-Queens ، فإن مهمة إنجاز n-Queens المعنية موضع مميز بسبب تعقيدها. في عملهم ( أظهر Gent at all (2017)) أن مشكلة n-Queens إكمال تنتمي إلى مجموعة NP-Complete ( أظهرت أن n-Queens Complete على حد سواء NP-Complete و # P-Complete ). من المفترض أن حل هذه المشكلة قد يفتح الطريق أمامنا لحل بعض المشكلات الأخرى من مجموعة NP-Complete .

المشكلة وضعت على النحو التالي. هناك تركيبة من ملكات k ، والتي يتم توزيعها باستمرار على رقعة الشطرنج بحجم nxn . يجب إثبات أنه يمكن إكمال هذا التكوين إلى حل كامل ، وإعطاء حل واحد على الأقل ، أو لإثبات أن هذا الحل غير موجود. هنا ، بالتناسق ، نعني تركيبة من ملكات k يتم استيفاء ثلاثة شروط للمشكلة: في كل صف وفي كل عمود وأيضًا على الأقطار اليسرى واليمنى التي تمر عبر الخلية حيث توجد الملكة ، ولا يوجد أكثر من ملكة واحدة. تمت صياغة المشكلة في هذا النموذج لأول مرة بواسطة Nauk (1850) .

1.1 التعاريف

فيما يلي ، سنشير إلى حجم جانب رقعة الشطرنج بالرمز n . سيتم استدعاء حل كامل إذا تم وضع جميع ملكات n باستمرار على رقعة الشطرنج. جميع الحلول الأخرى ، عندما يكون عدد k للملكات الموضوعة بشكل صحيح أقل من n - سنتصل بالتركيب. نسمي تركيبة k queens إيجابية إذا كان يمكن إكمالها قبل حل كامل. وفقًا لذلك ، فإن التكوين الذي لا يمكن إكماله حتى يتم استدعاء الحل الكامل سالب. كتناظرية لـ "رقعة الشطرنج" بحجم nxn ، سننظر أيضًا في "مصفوفة حل" بحجم nxn . على سبيل المثال ، سيتم تقديم جميع الخوارزميات التي تم تطويرها لحل المشكلة بلغة ماتلاب.

أجريت الدراسة على أساس المحاكاة الحاسوبية (المحاكاة الحاسوبية). لاختبار هذه الفرضية أو تلك ، أجرينا تجارب حسابية في مجموعة واسعة من القيم n = (10 ، 20 ، 30 ، 40 ، 50 ، 60 ، 70 ، 80 ، 90 ، 100 ، 200 ، 300 ، 500 ، 1000 ، 1000 ، 3000 ، 5000 ، 10000 ، 30،000 ، 50،000 ، 80،000 ، 10 ⁵ ، 3 * 10 ⁵ ، 5 * 10 ⁵ ، 10 ⁶ ، 3 * 10 ⁶ ، 5 * 10 ⁶ ، 10 ⁷ ، 3 * 10 ⁷ ، 5 * 10 ⁷ ، 8 * 10 ⁷ ، 10 ⁸ ) ، واعتمادًا على قيمة n ، تم إنشاء عينات كبيرة بما يكفي للتحليل. نسمي هذه القائمة " قائمة أساسية بقيم n " لإجراء تجارب حسابية. تم تنفيذ جميع الحسابات على جهاز كمبيوتر عادي. في وقت التجميع (أوائل 2013) ، كان التكوين ناجحًا إلى حد ما: وحدة المعالجة المركزية - Intel Core i7-3820 ، 3.60 جيجا هيرتز ، ذاكرة الوصول العشوائي 32.0 جيجابايت ، GPU-NVIDIA Ge Forse GTX 550 Ti ، جهاز القرص- ATA Intel SSD ، SCSI ، OS- نظام التشغيل 64 بت نظام التشغيل Windows 7 Professional . نسمي هذه المجموعة ببساطة - سطح المكتب 13 .

2. إعداد البيانات

تبدأ الخوارزمية بقراءة الملف الذي يحتوي على صفيف أحادي البعد من البيانات حول توزيع التكوين التعسفي للملكات k . من المفترض أن يتم إعداد البيانات بالطريقة التالية. دع هناك صفيف صفري Q (i) = 0 ، i = (1 ، ... ، n) ، حيث تتوافق مؤشرات خلايا هذه المجموعة مع مؤشرات الصفوف في مصفوفة الحل. إذا كانت هناك ملكة في الموضع j في بعض الصف التعسفي i لمصفوفة الحل ، فسيتم تنفيذ الواجب Q (i) = j . وبالتالي ، فإن حجم التكوين k ، سيكون مساوياً لعدد الخلايا غير الصفرية للصفيف Q. (على سبيل المثال ، Q = (0 ، 0 ، 5 ، 0 ، 4 ، 0 ، 0 ، 3 ، 0 ، 0) تعني أننا نفكر في تكوين k = 3 ملكات في المصفوفة n = 10 ، حيث توجد الملكات في الثالثة ، الخطان الخامس والثامن ، على التوالي في المناصب: 5 ، 4 ، 3).

3. خوارزمية للتحقق من صحة مشكلة حل كوينز

للبحث ، نحتاج إلى خوارزمية تسمح لنا بتحديد صحة حل مشكلة n-Queens في وقت قصير. التحكم في موقع الملكات في كل صف وكل عمود بسيط. السؤال يدور حول الحدود القطرية. يمكننا أن نبني خوارزمية فعالة لمثل هذه الحسابات إذا استطعنا تعيين كل خلية من مصفوفة الحل لخلية معينة من متجه تحكم معين من شأنها أن تميز بشكل فريد تأثير القيود القطرية على الخلية المعنية. بعد ذلك ، استنادًا إلى ما إذا كانت خلية متجه التحكم حرة أو مشغولة ، يمكن للمرء الحكم على ما إذا كانت الخلية المقابلة لمصفوفة القرار حرة أم مغلقة.استخدم Sosic & Gu (1990) هذه الفكرة لأول مرة لمراعاة وتجميع عدد حالات الصراع بين المواقف المختلفة للملكات. نستخدم فكرة مماثلة في الخوارزمية الموضحة أدناه ، ولكن فقط لنأخذ في الاعتبار ما إذا كانت خلية مصفوفة الحلول مجانية أم مشغولة. يوضح الشكل 1 ، على سبيل المثال ، رقعة شطرنج 8 × 8 فوقها يوجد تسلسل مكون من 24 خلية أعلاه .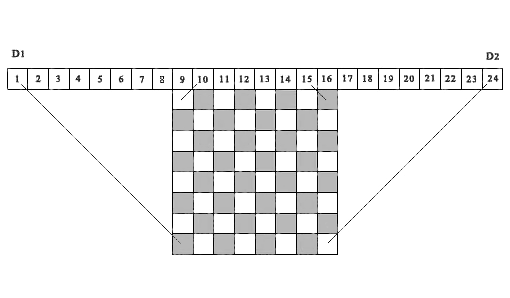


التين. 1. مثال توضيحي لمراسلات الإسقاطات القطرية لخلايا المصفوفة مع الخلايا المقابلة في مصفوفة التحكم D1 و D2 ، ( ن = 8)

النظر في أول 15 خلية كعناصر من متجه التحكم D1. تقع إسقاطات جميع الأقطار اليسرى من أي خلية من مصفوفة المحلول في إحدى خلايا ناقل التحكم D1 . في الواقع ، توجد كل هذه الإسقاطات داخل قطاعي خط متوازيين ، يربط أحدهما خلية المصفوفة (8.1) بالخلية الأولى من المتجه D1 ، بينما يربط الثاني خلية المصفوفة (1.8) بالخلية 15 من متجه التحكم D1 . نقدم تعريفًا مشابهًا للتوقعات القطرية المائلة. للقيام بذلك ، انقل الأصل من الخلية 1 إلى الخلية 9 إلى اليمين ، والنظر في تسلسل مكون من 16 خلية كعناصر في ناقل التحكم D2(في الشكل ، هذه هي خلايا من التاسع إلى الرابع والعشرين). ستقع إسقاطات جميع الأقطار الصحيحة من أي خلية في مصفوفة المحلول في إحدى خلايا متجه التحكم هذا ، بدءًا من الخلية الثانية إلى السادسة عشرة (في الشكل ، من 10 ث إلى 24 عشر). هنا ، تقع كل هذه التوقعات بين جزأين من الخطوط المتوازية - الجزء الذي يربط الخلية (8،8) من مصفوفة المحلول مع الخلية 16 من المتجه D2 (الخلية 24 في الشكل) والجزء الذي يربط الخلية (1،1) من مصفوفة الحل بالخلية 2 من مكافحة ناقلات D2 (الخلية 10 في الشكل). إن إسقاطات جميع خلايا مصفوفة المحلول الملقاة على نفس القطر الأيسر تقع في نفس خلية متجه التحكم الأيسر D1، على التوالي ، تقع إسقاطات جميع خلايا مصفوفة المحلول الملقاة على نفس القطر الأيمن في نفس خلية متجه التحكم الأيمن D2 . وبالتالي ، فإن متجهي التحكم هذين D1 و D2 ، يسمحان بالتحكم الكامل في جميع مثبطات قطري لأي خلية من مصفوفة القرار.

من المهم الإشارة إلى أن فكرة استخدام الإسقاطات القطرية على خلايا متجهات التحكم لتحديد ما إذا كانت خلية مصفوفة الحل مع الإحداثيات (i، j) مجانية أم مشغولة تم تنفيذها لاحقًا في Richards (1997). يوفر واحدة من أسرع خوارزميات البحث العودية لجميع الحلول ، استنادًا إلى العمليات باستخدام قناع بت. الفرق المهم هو أن الخوارزمية المشار إليها مصممة للبحث المتسلسل لجميع الحلول ، بدءًا من الصف الأول من مصفوفة الحلول - أو من الصف الأخير من المصفوفة - الأعلى. تستند الخوارزمية التي اقترحناها إلى أن اختيار رقم كل سطر لموقع الملكة يجب أن يكون تعسفيًا. بالنسبة للخوارزمية قيد النظر ، هذا أمر ذو أهمية أساسية. لاحظ أن الشكل 1 أعلاه ، بنينا قياسًا على ما تم نشره في هذه الورقة.
برنامج للتحقق من صحة حل معين لمشكلة n-Queens ، أو ما إذا كان تكوين معين من k صحيحًاكوينز على النحو التالي.

1. للتحكم في المثبطات القطرية ، قم بإنشاء صفيفين D1 (1: n2) و D2 (1: n2) ، حيث n2 = 2 * n ، ومصفوفة B (1: n) للتحكم في شغل أعمدة مصفوفة الحل. صفر من هذه المصفوفات الثلاثة.

2. نقدم عداد عدد الملكات التي تم تثبيتها بشكل صحيح ( totPos = 0 ). بشكل متسق ، في دورة ، بدءًا من السطر الأول ، نعتبر جميع مواقف الملكات المقدمة. إذا كانت Q (i)> 0 ، ثم استنادًا إلى فهرس الصف i ومؤشر موضع الملكة في هذا الصف j = Q (i) ، فإننا نشكل المؤشرات المقابلة لصفيف التحكم D1 (r) و D2 (t) :
r = n + j - i
t = j + i

3. إذا كانت كل الشروط ( D1 (r) = 0 ، D2 (t) = 0 ، B (j) = 0 ) راضية ، فهذا يعني أن الخلية ( i، j) مجاني ولا يقع في منطقة الإسقاط الخاصة بالقيود القطرية المشكلة من الملكات التي تم إنشاؤها مسبقًا. موقف الملكة في هذا الموقف هو الصحيح. إذا لم يتم استيفاء واحد على الأقل من هذه الشروط ، فسيكون اختيار هذا المنصب خاطئًا ، على التوالي ، وسيكون القرار خاطئًا.

4. إذا كان الحل صحيحًا ، فقم بزيادة عداد عدد الملكات التي تم تثبيتها بشكل صحيح ( totPos = totPos + 1 ) ، وأغلق الخلايا المقابلة من صفائف التحكم: (D1 (r) = 1 ، D2 (t) = 1 ، B (j) = 1) . لذلك نحن نغلق جميع الخلايا في العمود(ي) وتلك الخلايا من مصفوفة الحل التي تقع على طول الأقطار اليسرى واليمنى تتقاطع في الخلية (أنا ، ي) .

5. كرر إجراء التحقق لجميع المواقع المتبقية.
ربما تكون هذه واحدة من أسرع الخوارزميات لتقييم صحة الحل لمشكلة n-Queens . يبلغ وقت التحقق من مليون موقع لمصفوفة الحلول 10 ⁶ × 10 ⁶ على سطح المكتب 13 0.175 ثانية ، وهو ما يتوافق مع وقت الضغط على مفتاح "Enter" تقريبًا. من الواضح أن هذه الخوارزمية خطية فيما يتعلق بحساب الوقت فيما يتعلق بـ n .

4. وصف الخوارزمية لحل المشكلة

العام . مشكلة n-Queens إكمال مشكلة كلاسيكية غير حتمية. ترتبط الصعوبة الرئيسية في حلها بمسألة اختيار مؤشر الصفوف وفهرس الموقف في هذا الصف ، في الظروف التي تكون فيها مساحة الولاية ضخمة. عند البحث عن جميع الحلول الممكنة ، لا تنشأ مثل هذه المشكلة. يجب مراعاة جميع فروع البحث الصالحة في مساحة الولاية ، ولا يهم الترتيب الذي يتم اعتبارها به. ومع ذلك ، عند الحاجة إلى إكمال التكوين التعسفي للملكات k حتى حل كامل ، فإننا في هذه الحالة نحتاج إلى خوارزمية لاختيار مؤشرات الأعمدة والصفوف التي تتعرف بشكل ملائم على التركيب الحالي وتؤدي إلى حل أسرع من غيرها. في هذا المشروع ، قررنا مسألة الاختيار على أساس الموقف العام التالي - إذا لم نتمكن من صياغة الشروط التي تعطي الأفضلية لأي صف أو أي موضع في هذا الصف على الآخرين ، فإننا نستخدم خوارزمية اختيار عشوائي بناءً على توزيع أرقام عشوائية بالتساوي . طريقة اختيار عشوائية مماثلة لحل المشاكل التي يكون فيها مساحة الدولة ضخمة للغاية. تم تخصيص إحدى إصدارات سلسلة وقائع ورشة عمل DIMACS (1999) تمامًا لاستخدام الانتقاء العشوائي في تطوير الخوارزميات لحل المشكلات المعقدة. يمكن أن يكون التنفيذ الصحيح لخوارزمية الاختيار العشوائي حلاً مثمرًا إلى حد ما ، على الرغم من أن هذا شرط ضروري ولكنه غير كاف لإكمال الحل. تعتبر Sosic and Gu (1990) واحدة من أولى الدراسات التي استخدمت خوارزمية اختيار عشوائي لحل مشكلة n-Queens . تعتمد الخوارزمية التي درسوها على فكرة بسيطة وموجزة إلى حد ما. دع هناك سلسلة من الأرقام من 1 إلى n ، والتي يتم إعادة ترتيبها بشكل عشوائي. هذه المجموعة من الأرقام لها خاصية مهمة. يتكون في حقيقة أنه بغض النظر عن كيفية توزيع هذه الأرقام على صفوف مختلفة من مصفوفة الحلول كمواقف للملكة (رقم واحد في كل سطر) ، فسيتم دائمًا تنفيذ أول قاعدتين في بيان المشكلة: كل صف ولن يحتوي كل عمود أكثر من ملكة واحدة. ومع ذلك ، فقط جزء من المواقف التي تم الحصول عليها بهذه الطريقة سيكون خاليًا من القيود القطرية. الجزء الآخر سيكون في حالة "تعارض" مع الملكات التي تم تأسيسها مسبقًا. للخروج من هذا الموقف ، استخدم المؤلفون طريقة المقارنة بين المواقف المتعارضة وتبادلها من أجل الحصول على حل كامل. في الخوارزمية المقترحة لدينا ، تكون حالات الصراع مستحيلة ، لأنه في كل خطوة من خطوات حل المشكلة ، يتم تثبيت الملكة في خلية السطر المعني فقط إذا كانت الخلية خالية.

1.4 اختيار نموذج لتتبع الظهر (BT)

في عملية إيجاد حل لمشكلة ما ، قد ينشأ موقف ما عندما تؤدي سلسلة متسلسلة من الحلول إلى طريق مسدود. هذه خاصية "وراثية" للمشاكل غير الحتمية. في هذه الحالة ، تحتاج إلى العودة إلى إحدى الخطوات السابقة ، واستعادة حالة المهمة وفقًا لهذا المستوى والبدء مرة أخرى في البحث عن حل من هذا الموضع. السؤال هو أي من المستويات السابقة يجب أن تعاد وكم يجب أن تكون هذه المستويات (حسب المستوى ، نعني خطوة معينة في حل المشكلة مع عدد معين من الملكات المثبتة بشكل صحيح). من الواضح أن اختيار مستوى الحل للرجوع إليه هو بنفس أهمية اختيار فهرس الصفوف أو فهرس الموضع في هذا الصف. لذلك ، بغض النظر عن النهج المتبع لحل هذه المشكلة ، من الضروري أولاً تحديد عدد المستويات الأساسية للعودة ، وكذلك آلية وشروط العودة إلى أحد هذه المستويات. في الخوارزمية المقترحة ، نقسم مصفوفة الحلول إلى ثلاثة مستويات أساسية. هذه هي نقاط العودة. في حالة حدوث حالة توقف تام نتيجة لهذا الحل ، وبناءً على معايير المهمة ، نعود إلى أحد هذه المستويات الأساسية الثلاثة. يتوافق المستوى الأساسي الأول ( baseLevel1 ) مع الحالة عند اكتمال التحقق من بيانات التكوين المعني. هذه هي بداية البرنامج. تعتمد قيم مستويي الأساس التاليين ( baseLevel2 و baseLevel3 ) على حجم المصفوفة n . تم تأسيس الاعتماد التجريبي لهذه القيم الأساسية على حجم مصفوفة الحل على أساس عدد كبير من التجارب الحسابية. للحصول على تمثيل أكثر دقة لهذا الاعتماد ، قمنا بتقسيم الفاصل الزمني المدروس بالكامل من 7 إلى ^{8 8} إلى جزأين. دع u = log (n) ، ثم إذا كان n <30 000 ، إذن

قاعدة المستوى 2 = ن - الجولة (12.749568 * u3 - 46.535838 * u2 + 120.011829 * u - 89.600272)
قاعدة المستوى 3 = ن - الجولة (9.717958 * u3 - 46.144187 * u2 + 101.296409 * u - 50.669273)

وإلا

baseLevel2 = n - round (-0.886344 * u3 + 56.136743 * u2 + 146.486415 * u + 227.967782)
قاعدة المستوى 3 = ن - الجولة (14.959815 * u3 - 253.661725 * u2 + 1584.713376 * u - 3060.691342)

4.2 هيكل كتلة

يتم إنشاء الخوارزمية في شكل سلسلة من خمس كتل أحداث ، حيث يرتبط كل حدث بتنفيذ جزء معين من حل المشكلة. تختلف خوارزميات المعالجة في كل كتلة عن بعضها البعض. تعمل ثلاثة فقط من الكتل الخمسة على تشكيل سلسلة متتالية من الحلول ، والكتلان المتبقيتان تعدان تحضيرية. يعتمد اختيار رقم الكتلة الذي تبدأ منه الحسابات على قيمة n وعلى نتائج مقارنة حجم التركيب k مع قيم baseLeve2 و baseLevel3 . استثناء هو الفاصل الزمني للقيم n = (7 ، ... ، 99) ، والتي يمكن أن يطلق عليها "منطقة مضطربة" بسبب خصوصيات سلوك الخوارزمية في هذا القسم. بالنسبة للقيم n = (7 ، ... ، 49) ، بغض النظر عن حجم التكوين ، بعد إدخال البيانات ومراقبتها ، تبدأ الحسابات من الكتلة الرابعة. بالنسبة للقيم n = (50 ، ... ، 99) ، اعتمادًا على حجم التكوين ، تبدأ الحسابات إما من الكتلة الثانية أو من الرابعة. كما ذكر أعلاه ، في كل خطوة من خطوات حل المشكلة ، تعتبر فقط تلك المواقف الموجودة في السطر والتي لا تدخل في نطاق القيود التي أنشأتها الملكات المحددة مسبقًا. هذه هي المواقف التي تسمى مجانا .
دعنا نصف بإيجاز العمليات الحسابية التي يتم تنفيذها في كل من هذه الكتل الخمس للبرنامج.

4.3 بداية الخوارزمية

يتم إدخال البيانات ويتم التحقق من التكوين للتأكد من صحتها. في كل خطوة تحقق ، يتم تغيير خلايا صفائف التحكم. يتم حساب عدد الملكات المثبتة بشكل صحيح. في حالة عدم وجود أخطاء في التكوين ، يستمر الحل ، وإلا يتم عرض رسالة خطأ. بعد اكتمال التحقق ، يتم إنشاء نسخ من المصفوفات الرئيسية لإعادة استخدامها على هذا المستوى. بعد ذلك ، يتم نقل التحكم إلى Block-1 .

4.4 بلوك 1

بداية تشكيل فرع البحث. نحن نعتبر ك كوينز الموجودة على رقعة الشطرنج كنقطة انطلاق. يجب الاستمرار في إكمال هذا التكوين ووضع الملكات على رقعة الشطرنج حتى يصبح العدد الإجمالي مساويًا لـ baseLevel2 . تسمى الخوارزمية المستخدمة هنا randSet & randSet . ويرجع ذلك إلى حقيقة أننا هنا نقارن باستمرار قائمتين عشوائيتين من المؤشرات ، في البحث عن أزواج خالية من القيود القطرية المقابلة. للقيام بذلك ، يتم تنفيذ الإجراءات التالية:

أ) يتم تشكيل قائمتين: قائمة بمؤشرات الصف المجاني وقائمة بمؤشرات الأعمدة المجانية ؛

ب) إعادة ترتيب الأرقام بشكل عشوائي في كل من هذه القوائم ؛

ج) في حلقة ، يُعتبر كل زوج متتابع من القيم (i ، j) ، حيث يتم تحديد الفهرس (i) من قائمة مؤشرات الصفوف المجانية والفهرس (j) من قائمة مؤشرات الأعمدة المجانية ، موضع الملكة المحتمل ويتم التحقق مما إذا كان هذا موقف في منطقة الإسقاط استثناءات قطري.

إذا لم تنتهك قاعدة الاستثناءات القطرية ، فيُعتبر الموضع صحيحًا وتوضع الملكة في هذا الموضع. بعد ذلك ، يتم زيادة العداد لعدد الملكات المثبتة بشكل صحيح ، ويتم تغيير الخلايا المقابلة من صفائف التحكم. إذا كان الموضع (i ، j) يقع في منطقة القيود المائلة التي تشكلها الملكات المحددة مسبقًا ، فلن يتغير أي شيء ويحدث الانتقال إلى الأخذ في الاعتبار زوج القيم التالي.

عند اكتمال دورة المقارنة لجميع أزواج القائمة ، بناءً على المؤشرات المتبقية الموجودة في منطقة الاستبعاد القطرية ، يتم تكوين قائمة بمؤشرات الصفوف الحرة المتبقية والأعمدة الحرة مرة أخرى ، ويتكرر هذا الإجراء حتى يتم العدد الإجمالي للملكات الموضوعة بشكل صحيح (totPos ) لن تكون مساوية أو تتجاوز قيمة الحد لـ baseLevel2 . بمجرد الوفاء بهذا الشرط ، يتم نقل التحكم إلى المربع 2 . إذا اتضح أنه نتيجة للبحث عن حل ، فقد نشأ موقف من القائمة الكاملة لمؤشرات الصفوف الحرة المتبقية والأعمدة المجانية ، لا يكون أي من الأزواج مناسبًا لموقع الملكة ، ثم في هذه الحالة ، تتم استعادة القيم الأصلية لصفائف التحكم استنادًا إلى النسخ التي تم إنشاؤها مسبقًا ، ويتم نقل السيطرة إلى بداية Block-1 لإعادة العد.

4.5 بلوك 2

هذه الكتلة بمثابة مرحلة تمهيدية للانتقال إلى Block-3 . في هذا المستوى ، يكون عدد الخطوط الحرة المتبقية ( freeRows ) أقل بكثير من n . يسمح لك هذا بنقل الأحداث من المصفوفة الأصلية للحجم nxn إلى مصفوفة بحجم أصغر L (1: freeRows ، 1: freeRows) . علاوة على ذلك ، استنادًا إلى المعلومات المتعلقة بالصفوف الحرة المتبقية والأعمدة الحرة في مصفوفة القرار الأصلية ، تتم كتابة الأصفار إلى الخلايا المقابلة في الصفيف L ، مشيرة إلى أن هذه الخلايا خالية. باستخدام انتقال "الإسقاط" هذا ، يتم الحفاظ على المراسلات الخاصة بمؤشرات الصفوف والأعمدة في المصفوفة الجديدة مع مؤشرات المصفوفة الأصلية المقابلة. من المهم ملاحظة أنه على الرغم من أنه في عملية حل هذه المشكلة ، فإن جميع الأحداث تتكشف على المصفوفة الأولية للحجم nxn ، وهذه المصفوفة هي الساحة الرئيسية للعمل ، في الواقع لم يتم إنشاء مثل هذه المصفوفة ، وفقط التحكم في صفائف المحاسبة لمؤشرات الصفوف A (1: n) و الأعمدة B (1: n) من هذه المصفوفة.

جنبا إلى جنب مع مجموعة L ، يتم تشكيل صفيفين للعمل rAr (1: freeRows) و tAr (1: freeRows) في هذه الكتلة أيضًا لحفظ المؤشرات المقابلة لصفيف التحكم D1 و D2 . هذا يرجع إلى حقيقة أنه عندما نقوم بتثبيت الملكة التالية في الخلية (i ، j) من المصفوفة الأولية للحجم nxn ، ثم بعد ذلك يجب أن نستبعد خلايا المصفوفة L التي تقع في منطقة الإسقاط للاستثناءات القطرية للصفيف "الكبير" الأصلي. نظرًا لأن التحكم بالقيود القطرية يتم فقط داخل المصفوفة الأصلية للحجم nxn ، فإن وجود مصفوفات العمل rAr و tAr يتيح لنا الحفاظ على المراسلات وترجمة الخلايا الممنوعة إلى حدود المصفوفة L. وهذا يبسط إلى حد كبير محاسبة المواقع المستبعدة.
بعد الانتهاء من العمل التحضيري في هذه المجموعة ، يتم إنشاء نسخ من المصفوفات الرئيسية لإعادة استخدامها على هذا المستوى ، ويتم نقل السيطرة إلى Block-3 .

4.6 بلوك 3

في هذه الكتلة ، يستمر تكوين فرع البحث عن الحلول على أساس البيانات المعدة في الكتلة السابقة. عدد الأسطر التي يتم فيها تعيين الملكات بشكل صحيح يساوي أو أكبر من baseLevel-2 . يجب متابعة الانتقاء حتى يساوي عدد الملكات التي تم تثبيتها على baseLevel-3 . نحن هنا نستخدم خوارزمية البحث عن حلول rand & rand ، أي لتكوين موضع الملكة ، بدلاً من قائمة الفهارس المجانية ، يتم استخدام فهارسين فقط ، وقيمة فهرس عشوائي لصف حر وقيمة فهرس عشوائية لموضع حر في هذا الصف. يتم تكرار هذا الإجراء دوريًا حتى يكون العدد الإجمالي للملكات الموضوعة مساوياً لقيمة baseLevel-3 . بمجرد استيفاء هذا الشرط ، يتم نقل التحكم إلى Block-4 . إذا تبين ، نتيجة العمليات الحسابية ، أن فرع البحث قد وصل إلى طريق مسدود ، فسيتم إغلاق هذا القسم من تشكيل فرع البحث ويعود إلى بداية المربع 3 ، حيث يتم تكرار الحسابات مرة أخرى. لهذا ، تتم استعادة القيم الأولية لجميع صفائف التحكم.

4.7 بلوك 4

في هذه المجموعة ، يتم إعداد البيانات لنقل التحكم إلى Block-5 . في هذه الخطوة ، بعد الانتهاء من الإجراء في Block-3 ، أصبح عدد الخطوط المجانية ( nRow ) أقل. لذلك ، من المفيد أيضًا ترجمة الأحداث من صفيف أكبر إلى صفيف أصغر. يتيح لنا هذا النهج الفرصة لتحديد الخصائص الضرورية للخطوط المتبقية التي نحتاجها في هذه المرحلة بسرعة. تكتسب أهمية خاصة ، على أساس هذه المجموعة ، التنبؤ بفرص فرع البحث للعديد من الخطوات إلى الأمام دون الحاجة إلى إكمال العمليات الحسابية. الشرط بسيط جدا. إذا تبين أنه من بين الخطوط المجانية المتبقية يوجد خط لا يوجد فيه موضع حر ، ثم يتم إغلاق فرع البحث قيد النظر ويتم نقل التحكم إلى إحدى كتل المستوى الأدنى. الإجراءات التحضيرية التي تم تنفيذها هنا تشبه إلى حد كبير ما تم في Block-2 . استنادًا إلى المؤشرات الأصلية للصفوف الحرة والأعمدة المجانية ، يتم تشكيل صفيف ثنائي الأبعاد جديد ، تتوافق قيمه الصفرية مع المواضع المجانية في مصفوفة الحلول الأصلية. بالإضافة إلى ذلك ، يتم إنشاء مجموعة خاصة E (1: nRow ، 1: nRow) في هذه الكتلة ، بناءً على ذلك يمكنك تحديد عدد المواضع المجانية في الخطوط الحرة المتبقية التي سيتم إغلاقها إذا حددت الموضع (i ، j) لتعيين الملكة في مصفوفة المصدر. قبل نقل التحكم إلى المربع 5 ، يتم تنفيذ الإجراءات التالية:

تحديد عدد الوظائف الشاغرة في جميع الخطوط المتبقية ،

ب) يتم فرز مجموعة من مجموع المواقف المجانية ، للخطوط التي تم النظر فيها ، بترتيب تصاعدي ،

ج) إذا كانت جميع الخطوط المجانية المتبقية لها مراكز حرة (أي أن الحد الأدنى للقيمة في هذه القائمة المرتبة يختلف عن 0) ، عندئذ يتم نقل التحكم إلى Block-5.

إذا اتضح أنه في أي من الخطوط المتبقية لا يوجد موضع حر ، تتم استعادة المصفوفات اللازمة بناءً على النسخ المخزنة ، وبناءً على معلمات المهمة ، يتم نقل التحكم إلى أحد المستويات الأساسية.

د) يتم إنشاء نسخ احتياطية من جميع صفائف التحكم لهذا المستوى 4.

4.8 بلوك 5

هذه المرحلة نهائية ، وهنا ، يتم إجراء تكوين فرع البحث "أكثر توازناً" و "عقلانية". هذا هو "الميل الأخير" ، فقط عدد قليل من الخطوط المجانية تبقى. ولكن في الوقت نفسه ، هذا هو الجزء الأكثر صعوبة. جميع الأخطاء التي من المحتمل أن تكون ارتكبت في المراحل السابقة من تشكيل فرع البحث عن حل ، في المجمل ، تظهر هنا - في شكل عدم وجود موقف حر في السطر.

يتم تنفيذ خوارزمية هذه الكتلة على أساس حلقتين متداخلتين ، يتم تنفيذ الحلقة الثالثة داخلهما. تتمثل إحدى ميزات الدورة الثالثة في إمكانية تكرارها ، دون تغيير معلمات دورتين خارجيتين. يحدث هذا إذا كان فرع البحث الذي تم إنشاؤه في حالة توقف تام. لا يتجاوز عدد هذه التكرارات القيمة الحدية للتكرار ، والتي تم تحديد القيمة المثلى لها على أساس التجارب الحسابية.

يرتبط مؤشر الحلقة الخارجية باختيار تسلسلي لمؤشرات الصف التي ظلت حرة بعد العمليات الحسابية في المستوى الأساسي الثالث. يتم ذلك بناءً على قائمة الصفوف التي تم ترتيبها مسبقًا حسب عدد المواضع المجانية في الصف. يبدأ التحديد بسطر ، مع أقل عدد ممكن من المواضع المجانية ثم ، في الخطوات اللاحقة ، بترتيب تصاعدي. داخل هذه الدورة ، يتم تشكيل دورة ثانية ، يتكرر مؤشرها على مؤشرات جميع المواقف المجانية في الصف المعني. الغرض من الدورة الأولى هو فقط تحديد فهرس أحد الخطوط المجانية على هذا المستوى. وفقًا لذلك ، فإن الغرض من الدورة الثانية هو اختيار موضع مجاني واحد فقط ضمن الخط المدروس. تحدث هذه الإجراءات فقط في المستوى الأساسي الثالث. بعد هذا الاختيار ، يتم زيادة عدد الملكات المثبتة ، ويتم تغيير الخلايا المقابلة لجميع صفائف التحكم. علاوة على ذلك ، يتم نقل التحكم داخل دورة متداخلة (ثالثة) ، تكون منطقة نشاطها بالفعل جميع الخطوط الحرة المتبقية. داخل هذه الدورة ، يتم تنفيذ اختيار فهرس الصف واختيار الموضع المجاني في هذا الصف بناءً على القواعد التالية:

أ) اختيار خط مجاني . يتم النظر في جميع الخطوط الحرة المتبقية ، ويتم تحديد عدد المراكز الحرة في كل سطر. يتم تحديد الصف الذي يكون فيه عدد المواضع المجانية ضئيلًا. وهذا يقلل من المخاطر المرتبطة بإمكانية استبعاد آخر المراكز الشاغرة في بعض الأسطر المتبقية التي تكون فيها الدولة في حدها الأدنى والحرج من حيث عدد الوظائف الشاغرة ( قاعدة الحد الأدنى للمخاطر ). بالمناسبة ، مع أخذ هذه القاعدة في الاعتبار ، يبدأ فهرس الدورة الأولى في هذه المجموعة الخامسة بتحديد متسلسل للصفوف مع الحد الأدنى لقيمة عدد المواضع المجانية في صف واحد. إذا تبين في بعض الخطوات أن للخطين نفس العدد الأدنى من المواضع الحرة ، فسيتم اختيار عشوائي لمؤشر واحد من الموضعين المدرجين أولاً في القائمة المرتبة. إذا كان عدد الصفوف التي لها نفس الحد الأدنى لعدد المواضع الحرة أكثر من صفين ، فسيتم اختيار عشوائي مؤشر واحد من المراكز الثلاثة المدرجة أولاً في قائمة الترتيب.

ب) اختيار موقف مجاني على التوالي .من قائمة جميع الوظائف الشاغرة في الصف المعني ، يتم اختيار موقع واحد يتسبب في الحد الأدنى من الضرر للمراكز الشاغرة في جميع الصفوف المتبقية. يتم ذلك على أساس الصفيف الذي تم تكوينه سابقًا E. بكلمة "الحد الأدنى من الضرر" ، نعني اختيار مثل هذا الموقف في سطر معين يستبعد أقل قدر من المواضع الحرة في جميع الخطوط المتبقية ( قاعدة الحد الأدنى من الضرر). إذا تبين أن اثنين أو أكثر من المواضع المجانية في صف واحد لها نفس القيم الدنيا وفقًا لمعيار الضرر ، فسيتم اختيار مؤشر أحد المواضع المدرجة في القائمة أولاً بشكل عشوائي. إن اختيار موقع يستبعد الحد الأدنى لعدد المواضع المجانية في الخطوط المتبقية يقلل من "الضرر" المرتبط بوضع الملكة في هذا الموضع. يتيح استخدام كل من هذه القواعد الاستخدام الرشيد للموارد في كل خطوة من خطوات تكوين فرع البحث. هذا يقلل بدرجة كبيرة من المخاطر ويزيد من احتمال اختيار تكوين تعسفي إلى حل كامل إذا كان التكوين المعني لديه حل. إذا تبين في خطوة ما من الحل أنه لا توجد وظائف شاغرة في أحد الأسطر المتبقية للنظر ، فسيتم إغلاق فرع البحث هذا. في هذه الحالة ،استنادًا إلى النسخ الاحتياطية ، تتم استعادة كافة صفائف التحكم ، وإذا كان عدد مرات تكرار التكرار لا يتجاوز قيمة الحدrepeatBound، ثم دون تغيير مؤشرات الدورتين الأولى والثانية الخارجية ، يتم تكرار عمل الدورة المتداخلة الثالثة مرة أخرى. ويرجع ذلك إلى حقيقة أنه في الحالات التي تزامنت فيها القيم الدنيا للمعايير ذات الصلة ، قمنا باختيار عشوائي. تتيح إعادة تشكيل فرع البحث وفقًا لشروط المستوى الأساسي استخدامًا أكثر فاعلية لـ "موارد البدء" المتوفرة في هذا المستوى. يكون عدد مرات البدء المتكررة للدورة المتداخلة الثالثة محدودًا ، وإذا تم تجاوز قيمة الحد ، يتم إيقاف تشغيل هذه الدورة. بعد ذلك ، تتم استعادة قيم صفائف التحكم ، ويتم نقل التحكم إلى دورة المستوى الأساسي الثالث للانتقال إلى قيمة الفهرس التالية. يتم تكرار هذا الإجراء بشكل دوري حتى يتم الحصول على حل كامل ، أو اتضح ذلكأننا استخدمنا جميع الخطوط المجانية وجميع المواقف المجانية في هذه الخطوط في هذا المستوى الأساسي. في هذه الحالة ، استنادًا إلى العدد الإجمالي للحسابات المتكررة على مختلف المستويات الأساسية ، ومع مراعاة حجم مصفوفة القرار وحجم التركيبة ، يعود المرء إلى أحد المستويات الأدنى للحسابات المتكررة ، أو يتم الحكم على أنه لا يمكن تكوين التركيبة المعنية مجهزة لإكمال الحل. في البرنامج ، من أجل الحد من الوقت الإجمالي لمشروع القانون ، فمن المقبول أن الإجراءأو يتم الحكم على أنه لا يمكن إكمال التكوين المعني حتى اتخاذ قرار كامل. في البرنامج ، من أجل الحد من الوقت الإجمالي لمشروع القانون ، فمن المقبول أن الإجراءأو يتم الحكم على أنه لا يمكن إكمال التكوين المعني حتى اتخاذ قرار كامل. في البرنامج ، من أجل الحد من الوقت الإجمالي لمشروع القانون ، فمن المقبول أن الإجراءلا يمكن تنفيذ التتبع الخلفي ، بغض النظر عن أي من المستويات السابقة التي تم إجراؤها عليها ، أكثر من مرات totSimBound . يتم تحديد هذه القيمة الحدودية بناءً على التجارب الحسابية لقيم مختلفة من n.

5. تحليل فعالية خوارزميات الاختيار

كفاءة خوارزمية randSet & randSet . لتحليل قدرات هذه الخوارزمية ، تم إجراء تجربة حسابية ، والتي تضمنت وضع ملكات في مصفوفة الحلول استنادًا إلى نموذج randSet & randSet طالما أن هذا الاحتمال موجود. بمجرد أن يصل فرع البحث إلى طريق مسدود ، أو تم الحصول على حل كامل ، تم إصلاح حجم التكوين ، وزمن الحل ، وتم تكرار الاختبار مرة أخرى. وأجريت التجارب الحسابية خارج القائمة الكاملة للقيم n . عدد الاختبارات المتكررة للقيم n = (30 ، 40 ، ... ، 90 ، 100 ، 200 ، 300 ، 500 ، 800 ، 1000) كان يساوي مليون ، بالنسبة للقيم المتبقية ، عدد الاختبارات ، مع زيادة n، انخفض تدريجياً من 100000 إلى 100. يسمح تحليل نتائج التجارب الحسابية باستخلاص النتائج التالية:

أ) كنتيجة للدورة الأولى فقط من إجراء randSet & randSet ، يتم وضع حوالي 60٪ من جميع الملكات بشكل صحيح في المتوسط. بالنسبة لـ n = 100 ، فإن عدد الملكات التي تم وضعها بشكل صحيح هو 60.05٪. مع زيادة في قيمة n ، تنخفض هذه القيمة تدريجياً ، وفي n = 10 ⁷ تصل إلى 59.97٪.

ب) المدرج التكراري لتوزيع قيم طول التراكيب التي تم الحصول عليها له نفس الشكل ، بغض النظر عن حجم مصفوفة القرار n. علاوة على ذلك ، تتميز جميعها بميزة مميزة - يختلف الجانب الأيسر للتوزيع (إلى القيمة الوسيطة) عن الجانب الأيمن. في الشكل 2 ، على سبيل المثال ، الرسم البياني المقابل


للشكل. 2. رسم بياني لتوزيع حلول أطوال مختلفة لنموذج randSet و randSet ( ن = 100 ، حجم العينة = 10 ⁶ ).

ن = 100. يبدو أن الرسم البياني يتم جمعه من توزيع التردد لحدثين مختلفين ، لأن تواتر حدوث الأحداث في الجزئين الأيسر والأيمن من التوزيع مختلف. لوصف هذا التوزيع ، من الأفضل استخدام وظيفتين لكثافة التوزيع الطبيعي ، إحداهما تغطي الفاصل الزمني إلى القيمة الوسيطة ، والآخر - الفاصل الزمني بعد القيمة الوسيطة.

ج) يزيد متوسط ​​قيمة عدد الملكات ( qMean ) التي يمكن تعيينها في مصفوفة القرار بناءً على هذه الخوارزمية مع n . كما يتضح من الشكل 3 ، حيث يتم تقديم رسم بياني لاعتماد نسبة qMean / n على حجم المصفوفة n ، تزداد هذه النسبة مع زيادة حجم المصفوفة. على سبيل المثال ،

الشكل. 3. اعتماد نسبة qMean / n على قيمة n لأحجام مختلفة من مصفوفة الحل. النموذج randSet & randSet ، qMean هو القيمة المتوسطة لطول الحل.

إذا كانت الخوارزمية لاختيار المواضع في مصفوفة بحجم 100 × 100 هي randSet & randSetيسمح "بدون توقف" بوضع الملكات في المتوسط ​​على 89 سطرًا ، ثم بالنسبة لمصفوفة 1000x1000 ، يرتفع عدد هذه الخطوط في المتوسط ​​إلى 967.

د) استنادًا إلى خوارزمية randSet & randSet ، يمكنك الحصول على حل كامل ، لكن "الإنتاجية" لهذا النهج منخفضة للغاية . كما يتضح من الشكل 4 ، بالنسبة


للشكل. 4. انخفاض احتمال الحصول على حل كامل في نموذج randSet & randSet مع زيادة في n .

قيم n = 7 ، احتمال الحصول على حل كامل هو 0.057 . علاوة على ذلك ، مع زيادة ناحتمال الحصول على حل كامل يتناقص بسرعة ، ويقارب الصفر من الصفر. بدءًا من القيمة n = 48 ، يكون احتمال الحصول على حل كامل في حدود 10 ^-6 . بعد قيمة العتبة n = 70 ، بالنسبة للقيم اللاحقة n ، لم يتم الحصول على حل كامل واحد (مع عدد الاختبارات يساوي مليون ).

e) ينشئ نموذج randSet & randSet فروع البحث بسرعة عالية جدًا. بالنسبة إلى n = 1000 ، يبلغ متوسط ​​الوقت اللازم للحصول على التركيبة 0.0015 ثانية. يبلغ متوسط ​​طول التراكيب 967. بناءً على ذلك ، بالنسبة إلى n = 10 ⁶متوسط ​​الوقت هو 2.6754 ثانية بمتوسط ​​طول أغنية يبلغ 999793.

و) باستثناء فترة زمنية صغيرة n <= 70 ، عندما يكون نموذج randSet & randSet في حالات نادرة جدًا قد يؤدي إلى حل كامل ، في جميع الحالات الأخرى ينتهي فرع القرار بتكوين تكوين سلبي ، والذي لا يمكن أن تكتمل حتى الحل الكامل. لذلك خوارزمية randSet و randSetلها ميزة مهمة - السرعة العالية لتشكيل فرع البحث ، والعيب الكبير هو أنه إذا تجاوز حجم التكوين قيمة عتبة معينة ، فإن هذه الخوارزمية تؤدي إلى تكوين تركيبات لا يمكن إكمالها حتى حل كامل. للتغلب على هذا العيب ، نوقف تشكيل فرع البحث عندما يتم الوصول إلى الحد الأدنى baseLevel-2 .

كفاءة خوارزمية راند وراند . لتحديد إمكانيات خوارزمية rand & rand ، تم إجراء محاكاة كمبيوتر مفصلة إلى حد ما للحصول على قائمة أساسية من القيم n . كما هو الحال مع نموذج randSet و randSet، كان عدد الاختبارات في معظم الحالات يساوي مليون . بالنسبة للقيم الأخرى ، انخفض عدد الاختبارات تدريجيًا من 100000 إلى 100.

تستند كلتا الخوارزميات إلى مبدأ الاختيار العشوائي. لذلك ، يجب أن نتوقع أن تكون الاستنتاجات المستخلصة هنا متطابقة بشكل أساسي مع الاستنتاجات الموضوعة لنموذج randSet & randSet . ومع ذلك ، يوجد اختلاف أساسي بينهما ، وهو يتألف مما يلي:

أ) نموذج rand & rand لا يعمل "بجد" مثل نموذج randSet & randSet . إذا تحدثنا عن بعض "مؤشر الاستخدام الرشيد للفرص المتاحة" ، نموذج راند وراندفي كل خطوة تستخدم الموارد بطريقة أكثر عقلانية. يؤدي هذا إلى حقيقة أنه ، على سبيل المثال ، عند n = 30 ، يكون احتمال الحصول على حل كامل 0.00170 في هذا النموذج أكبر 15 مرة من القيمة المماثلة البالغة 0.00011 لنموذج randSet & randSet . بالإضافة إلى ذلك ، هنا ، حتى قيمة العتبة n = 370 ، يبقى احتمال الحصول على حل كامل واحد على الأقل خلال مليون اختبار. بعد ذلك، قيمة العتبة للقيم اللاحقة ن عندما يكون عدد من الاختبارات على قدم المساواة إلى مليون، استنادا إلى نموذج راند راند و كان في استقبال أي حلول كاملة.

ب) هذه الخوارزمية أبطأ بكثير من خوارزمية randSet & randSet . إذا لn = 1000 لإنشاء تركيبة بحجم 967 ، سيكون متوسط ​​الوقت اللازم للحصول على تركيبة واحدة 0.0497 ثانية ، أي 33 أكثر من القيمة المقابلة البالغة 0.0015 لنموذج randSet & randSet .

سبب الاختلافات بين طريقتين متشابهتين بشكل أساسي للاختيار العشوائي يرجع إلى حقيقة أنه في نموذج randSet & randSet ، من أجل تسريع العمليات الحسابية ، لا يتم الاختيار العشوائي من القائمة المتبقية في كل خطوة. بدلاً من ذلك ، يتم اختيار زوج من المؤشرات بالتسلسل من قائمتين ، تم إعادة ترتيب عناصرهما بشكل عشوائي. هذا الاختيار ليس عشوائيًا إلى أقصى حد ، ومع ذلك ، فهو مناسب تمامًا لمنطق المشكلة ويسمح لك بالعد بسرعة.

لإظهار بصري تشغيل خوارزمية rand & rand، تم إجراء التجربة التالية:

أ) للحصول على رقعة شطرنج بحجم 100 × 100بعد كل خطوة من موقع الملكة في أي سطر ، تم تحديد عدد المواضع المجانية في كل من الخطوط المجانية المتبقية. وبالتالي ، بعد كل خطوة من خطوات حل المشكلة ، تلقينا قائمة الخطوط المجانية وقائمة مقابلة لعدد من المواقف المجانية في هذه الخطوط. جعل ذلك من الممكن بناء رسم بياني حيث يتم رسم مؤشرات أعمدة المصفوفة المعنية على طول محور الإحداثي ، وعدد المواضع الحرة المتبقية على طول محور الإحداثيات. للمقارنة ، تم إجراء الحسابات أيضًا لنموذج الاختيار المتسلسل للمواقع. عن طريق اختيار متسلسل يعني ما يلي. يعتبر السطر الأول ، حيث يتم اختيار أول موضع مجاني في القائمة. بعد ذلك ، يتم النظر في السطر الثاني ، حيث يتم تحديد أول موضع مجاني في القائمة ، إلخ. في الشكلين 5 و 6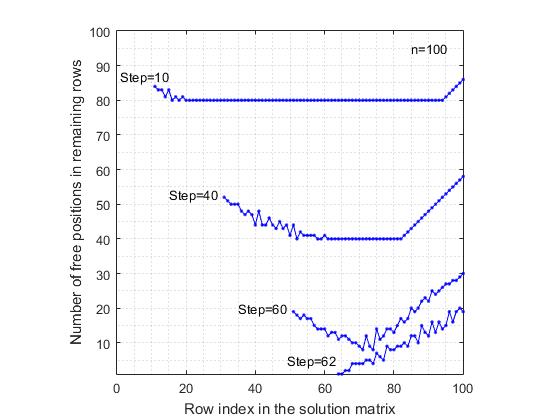


التين. 5. تقليل عدد المراكز الحرة في الخطوط الحرة المتبقية بعد وضع الملكات. اختيار منتظم بالتتابع للوظائف.

يتم عرض النتائج التي تتوافق مع النماذج قيد النظر. للتوضيح ، يعرض الرسم البياني النتائج فقط بعد الخطوات (10 ، 40 ، 60). بالنسبة لنموذج اختيار المواضع بالتتابع ، فإن آخرها هو الرسم البياني بعد الخطوة 62 ، لأن فرع البحث ينتهي بسبب عدم وجود موضع مجاني في الصف 63. من ناحية أخرى ، في نموذج rand & rand ، يتم تقديم الرسم البياني الأخير بعد الخطوة 70 من وضع الملكة ، على الرغم من أن متوسط ​​عدد الملكات التي تم وضعها بشكل صحيح يصل إلى 89 ، أي 26 خطوة أكثر من النموذج المتسلسل. عرض غريب للرسوم البيانية في نموذج rand & randنظرًا لأن مؤشر الصف يتم اختياره عشوائيًا بين الصفوف الحرة المتبقية ، وبالتالي فهي منتشرة بشكل عشوائي في مصفوفة الحل. توضح المقارنة بين هذين الشكلين أنه في النموذج المتسلسل لاختيار الموضع ، يكون مدى التباين في عدد المواضع الحرة أعلى من مثيله في نموذج rand & rand . ويرجع ذلك إلى حقيقة أنه مع التحديد المنتظم ، فإن القيود القطرية تستبعد بشكل غير منتظم المواضع الحرة في الصفوف المتبقية ، مما يؤدي إلى أن معدل الخفض في عدد المواضع الشاغرة في بعض الصفوف يكون أعلى منه في الصفوف الأخرى.


التين. 6. تقليل عدد المواضع الحرة في الخطوط الحرة المتبقية بعد وضع الملكات. نموذج تحديد المواقع هو راند وراند .

في المقابل ، مع اختيار عشوائي لمؤشر الصف الحر ومؤشر العمود الحر ، يتم توزيع مراكز الملكة بالتساوي على "المنطقة" من مصفوفة القرار ، مما يقلل من "متوسط" معدل الخفض في عدد المواضع المجانية في الصفوف المتبقية. وبالتالي ، مع مراعاة قدرات خوارزمية rand & rand ، نستخدمها في البرنامج لمواصلة تشكيل فرع البحث عن الحلول حتى يتم الوصول إلى مستوى baseLevel-3 .

تجدر الإشارة إلى أنه حتى لو لم تكن خوارزميات التحديد ( randSet & randSet ، rand & rand ) فعالة للغاية ، فسيتعين علينا استخدام بعض طرق التحديد العشوائي الأخرى عند تطوير الخوارزمية. هذا بسبب بيان المشكلة.مشكلة ن كوينز . إذا تخيلنا وجود خوارزمية مثلى معينة تحل المشكلة ، عند هذه الخوارزمية ، عند المدخلات ، ستتلقى دائمًا مجموعة عشوائية معينة من مؤشرات الأعمدة والصفوف. في كل مرة ستكون مجموعة عشوائية جديدة من مؤشرات الأعمدة والصفوف من مجموعة كبيرة من الاحتمالات. لكي تكون قادرًا على "استيعاب" الخوارزمية مثل مجموعة متنوعة من التراكيب العشوائية ، يجب أن تكون الخوارزمية نفسها مبنية على أساس الانتقاء العشوائي. يجب أن تكون المطابقة مثل مفتاح القفل . إذا بنينا الخوارزمية على هذا المبدأ ، ثم أي تكوين ثابت من كسيتم اعتبار الملكات كموقف (بدء) أولي في دورة صنع القرار. علاوة على ذلك ، سيكون الهدف فقط هو الاستمرار في تكوين فرع البحث عن حل حتى يتم إيجاد حل لتكوين معين ، أو يثبت أن هذا الحل غير موجود.

6. مثال على استخدام الحد الأدنى من قاعدة المخاطر (ن = 100)

في المرحلة الأولى من إيجاد حل ، عندما يكون عدد المواضع المجانية في الصفوف غير حاسم ، فإن اختيار فهرس الصف الحر ، أو مؤشر الموضع في هذا الصف ، ليس قاتلاً. ومع ذلك ، في المرحلة الأخيرة ، عندما يكون عدد المواضع المجانية في بعض الصفوف هو 1 أو 2 ، في هذه الحالة ، يجب عليك اختيار خوارزمية تحديد مختلفة. في هذا المستوى ، لن تعمل خوارزميات الاختيار العشوائي randSet & randSet و rand & rand .

يمكن توضيح سبب عدم عمل خوارزميات الاختيار العشوائي بواسطة المثال البسيط التالي. اسمح في خطوة ما بحل المشكلة ، للحصول على قيمة تعسفية لـ n ، في الصفوف المتبقية i ₁ ، i ₂ ، ... ، i _kعدد الوظائف الشاغرة (المشار إليها بين قوسين) هو: i ₁ (1) ، i ₂ (2) ، i ₃ (4) ، i ₄ (5) ، i ₅ (3) ، i ₆ (4) ، إلخ. إذا قمنا باختيار أي صف عشوائيًا ، ولكن ليس الصف i ₁ ، حيث يوجد موضع واحد مجاني فقط ، فقد يؤدي ذلك إلى وضع خطر عندما تؤدي الحظرات القطرية المتعلقة بموضع الملكة في السطر المحدد إلى إغلاق الموضع المجاني الوحيد في السطر أنا ₁ ، والتي سوف تقود الحل إلى طريق مسدود. من بين كل الصفوف i ₁ ، i ₂ ، ... ، i _kالأكثر ضعفا وحساسية لاختيار سلسلة هو مؤشر سلسلة ط ₁ . في مثل هذه الحالات ، يجب عليك أولاً تحديد الصف الذي تعتبر حالته الأكثر أهمية ويخلق خطرًا لحل المشكلة. لذلك ، في المرحلة الأخيرة من حل المشكلة ، في كل خطوة ، من الضروري اختيار موضع الخط بناءً على خوارزمية بسيطة من الحد الأدنى من المخاطر.

من أجل الوضوح ، دعونا ننظر ، على سبيل المثال ، في مصفوفة 100 × 100 ، المرحلة الأخيرة في تكوين حل حقيقي ، بعد الخطوة 88. حتى اكتمال المهمة ، بقي 12 خطًا مجانيًا ، تم العثور على عدد من المواضع المجانية لكل منها (يتم ترتيب الخطوط بالترتيب المتزايد لعدد الوظائف الحرة):الخطوة 89 - 25 (1) ، 12 (2) ، 22 (2) ، 82 (2) ، 88 (2) ، 7 (3) ، 64 (3) ، 3 (4) ، 76 (4) ، 91 (4) ، 4 (5) ، 96 (5) - يشير إلى فهرس الخط الحر ، وفي الأقواس - عدد المواضع المجانية في هذا الخط. وفقًا لقاعدة الحد الأدنى للمخاطر ، في الخطوة 89 من حل المشكلة ، يتم تحديد الصف 25 وهذا الموضع الحر الموجود فيه. نتيجة لإعادة الفرز ، تبقى لدينا 11 خطًا حرًا: الخطوات من 90 إلى 7 (2) و 12 (2) و 22 (2) و 82 (2) و 88 (2) و 3 (3) و 64 (3) ، 76 (3) ، 4 (4) ، 91 (4) ، 96 (4).كما ترى ، فإن عدد المواضع المجانية في الأسطر الخمسة الأولى هو نفسه ويساوي 2. لذلك ، يتم اختيار مؤشر أحد الخطوط الثلاثة الأولى بشكل عشوائي. في هذه الحالة ، تم تحديد الصف الثاني عشر وموضع الاثنين المتبقيين في هذا الصف ، مما يؤدي إلى الحد الأدنى من الضرر. وبالتالي ، في الخطوة 91 من تشكيل المحلول ، لدينا 10 خطوط حرة: Step-91 - 22 (1) ، 3 (2) ، 7 (2) ، 82 (2) ، 88 (2) ، 64 (3) 76 (3) ، 91 (3) ، 4 (4) ، 96 (4) . في هذه الخطوة ، يتم تحديد السطر 22 وهذا الموضع الحر الموجود فيه. استمرار بطريقة مماثلة ، تم تشكيل تسلسل القرارات التالية (الجدول 1). يتم عرض فهارس الصفوف المحددة بالخط العريض.

في هذا المثال بالذات ، في 11 حالة من أصل 12 ، كان هناك موقف في قائمة الخطوط الحرة المتبقية كان هناك سطر واحد على الأقل بقي فيه وضع حر واحد فقط. إذا لم نستخدم قاعدة الحد الأدنى للمخاطر ، فلن نتمكن من الوصول إلى النهاية. نظرًا لوجود "خطوة خاطئة" في اختيار فهرس لخط حر ، فمن المرجح أن يؤدي ذلك إلى تدمير الموضع الحر الوحيد الذي كان في أحد الخطوط الحرة المتبقية. هذا هو السبب عند استخدام خوارزمية randSet x randSet أو rand x rand فقط للحصول على حل كامل ، في المراحل الأخيرة ، يصل الحل إلى طريق مسدود.
تجدر الإشارة إلى أن خوارزمية الحد الأدنى للمخاطر لها معنى يومي بسيط ، وغالبًا ما تستخدم في صنع القرار. على سبيل المثال ، يعمل الطبيب أولاً وقبل كل شيء على المريض الذي تعتبر حالته حرجة للغاية للحياة ، وبالمثل ، فإن المزارع ، أثناء الجفاف الشديد ، يحاول إنقاذ الحصاد ، وفي المقام الأول يسقي تلك المناطق التي هي في حالة حرجة ...

7. تحليل كفاءة الخوارزمية

لتقييم كفاءة الخوارزمية لقيم مختلفة من n ، تم إجراء تجربة حسابية طويلة إلى حد ما (من حيث الوقت الكلي). في البداية ، تم تطوير خوارزمية سريعة إلى حد ما لإنشاء صفائف من الحلول nQueens Problem لقيمة تعسفية n. بناءً على هذا البرنامج ، تم تشكيل عينات كبيرة من الحلول للحصول على قائمة أساسية من القيم n. كانت أحجام العينات التي تم الحصول عليها من حلول nQueens Problem للقيم المختلفة لـ n على التوالي متساوية: (10) - 1000 ، (20 ، 30 ، ... ، 90 ، 100 ، 200 ، 300 ، 500 ، 800 ، 1000 ، 3000 ، 5000 ، 10،000 ، 100) - -10000 ، (30000 ، 50000 ، 80000) - 5000 ، (105 ، 3 * 105) - 3000 ، (5 * 105 ، 8 * 105 ، 106) - 1000 ، (3 * 106) - 300 ، ( 5 * 106) - 200 ، (10 * 106) - 100 ، (30 * 106) - 50 ، (50 * 106) - 30 ، (80 * 106 ، 100 * 106) - 20. هنا ، بين قوسين ، يشار إلى قائمة القيم n ، وتشير شرطة مزدوجة إلى حجم عينة من الحلول التي تم الحصول عليها.بعد ذلك ، تم تشكيل التراكيب العشوائية ذات الحجم التعسفي على أساس كل عينة من الحلول. على سبيل المثال ، لكل 10000 حل لـ n = 1000 ، تم تكوين 100 تركيبة عشوائية بحجم تعسفي. وكانت النتيجة عينة من مليون أغنية. نظرًا لأن أي تكوين ذي حجم تعسفي ، يتكون على أساس حل موجود ، يمكن إكماله مرة واحدة على الأقل حتى حل كامل ، كانت المهمة هي إكمال كل تكوين من العينة التي تم إنشاؤها إلى حل كامل يستند إلى خوارزمية حل مشكلة إكمال n-Queens . نظرًا لأنه في الخوارزمية قيد النظر في كل خطوة ، يتم تحديد الموضع الصحيح للملكة على رقعة الشطرنج ، وهنا ، من حيث المبدأ ، لا يمكنتم تكوين التراكيب العشوائية ذات الحجم التعسفي على أساس كل عينة من الحلول. على سبيل المثال ، لكل 10000 حل لـ n = 1000 ، تم تكوين 100 تركيبة عشوائية بحجم تعسفي. وكانت النتيجة عينة من مليون أغنية. نظرًا لأنه يمكن إكمال أي تكوين ذي حجم تعسفي ، تم تشكيله على أساس حل موجود ، مرة واحدة على الأقل حتى حل كامل ، كانت المهمة هي إكمال كل تكوين من العينة التي تم إنشاؤها إلى حل كامل يستند إلى خوارزمية حل مشكلة إكمال n-Queens . نظرًا لأنه في الخوارزمية قيد النظر في كل خطوة ، يتم تحديد الموضع الصحيح للملكة على رقعة الشطرنج ، وهنا ، من حيث المبدأ ، لا يمكنتم تكوين التراكيب العشوائية ذات الحجم التعسفي على أساس كل عينة من الحلول. على سبيل المثال ، لكل 10000 حل لـ n = 1000 ، تم تكوين 100 تركيبة عشوائية بحجم تعسفي. وكانت النتيجة عينة من مليون أغنية. نظرًا لأن أي تكوين ذي حجم تعسفي ، يتكون على أساس حل موجود ، يمكن إكماله مرة واحدة على الأقل حتى حل كامل ، كانت المهمة هي إكمال كل تكوين من العينة التي تم إنشاؤها إلى حل كامل يستند إلى خوارزمية حل مشكلة إكمال n-Queens . نظرًا لأنه في الخوارزمية قيد النظر في كل خطوة ، يتم تحديد الموضع الصحيح للملكة على رقعة الشطرنج ، وهنا ، من حيث المبدأ ، لا يمكنتم تشكيل 100 التراكيب العشوائية ذات الحجم التعسفي. وكانت النتيجة عينة من مليون أغنية. نظرًا لأن أي تكوين ذي حجم تعسفي ، يتكون على أساس حل موجود ، يمكن إكماله مرة واحدة على الأقل حتى حل كامل ، كانت المهمة هي إكمال كل تكوين من العينة التي تم إنشاؤها إلى حل كامل يستند إلى خوارزمية حل مشكلة إكمال n-Queens . نظرًا لأنه في الخوارزمية قيد النظر في كل خطوة ، يتم تحديد الموضع الصحيح للملكة على رقعة الشطرنج ، وهنا ، من حيث المبدأ ، لا يمكنتم تشكيل 100 التراكيب العشوائية ذات الحجم التعسفي. وكانت النتيجة عينة من مليون أغنية. نظرًا لأن أي تكوين ذي حجم تعسفي ، يتكون على أساس حل موجود ، يمكن إكماله مرة واحدة على الأقل حتى حل كامل ، كانت المهمة هي إكمال كل تكوين من العينة التي تم إنشاؤها إلى حل كامل يستند إلى خوارزمية حل مشكلة إكمال n-Queens . نظرًا لأنه في الخوارزمية قيد النظر في كل خطوة ، يتم تحديد الموضع الصحيح للملكة على رقعة الشطرنج ، وهنا ، من حيث المبدأ ، لا يمكنثم كانت المهمة هي إكمال كل تكوين من العينة التي تم إنشاؤها ، استنادًا إلى خوارزمية حل مشكلة إكمال n-Queens ، إلى حل كامل. نظرًا لأنه في الخوارزمية قيد النظر في كل خطوة ، يتم تحديد الموضع الصحيح للملكة على رقعة الشطرنج ، وهنا ، من حيث المبدأ ، لا يمكنثم كانت المهمة هي إكمال كل تكوين من العينة التي تم إنشاؤها ، استنادًا إلى خوارزمية حل مشكلة إكمال n-Queens ، إلى حل كامل. نظرًا لأنه في الخوارزمية قيد النظر في كل خطوة ، يتم تحديد الموضع الصحيح للملكة على رقعة الشطرنج ، وهنا ، من حيث المبدأ ، لا يمكنالقرارات الإيجابية الخاطئة (أي القرارات غير الصحيحة التي نعتبرها خطأً). ومع ذلك ، قد يكون هناك حلول سلبية خاطئة - في حالة عدم اكتمال أي تكوين مكون على أساس الحل الحالي بواسطة البرنامج حتى يكتمل الحل (على الرغم من أننا نعلم أن جميع التراكيب لها حل). عند إجراء تجربة حسابية في مجموعة واسعة من قيم n ، حددنا لأنفسنا الأهداف التالية:

أ) تحديد مدى تعقيد الخوارزمية ،

ب) لتحديد احتمال ظهور حلول سلبية خاطئة تظهر لقيم مختلفة من n ،

c) لتحديد التردد الذي يتم به استخدام إجراء التتبع الخلفي من أجل قيم مختلفة من ن.

وترد نتائج هذه التجربة الحسابية في الجدول 2.

الاستنتاج العام الذي يمكن استخلاصه على أساس النتائج التي تم الحصول عليها هو كما يلي:

أ) الخوارزمية تعمل بسرعة كافية. على سبيل المثال ، يبلغ متوسط ​​وقت التجميع للتكوين التعسفي للرقعة بحجم 1000 × 1000 ، والتي تم الحصول عليها على أساس مليون تجربة حسابية ، 0.062157 ثانية. هذا يعني أنه إذا كان للتكوين حل ، فسيتم العثور عليه فورًا بعد الضغط على مفتاح "Enter" . متوسط ​​وقت التجميع للتكوين التعسفي ، لجميع قيم n ، في حدود 7 إلى 30،000 ، لا يتجاوز ثانية واحدة.

ب) في كل عينة ، هناك ما يقرب من 10 ٪ من التراكيب ، والتي تتطلب المزيد من الوقت لإكمالها. مثل هذه التراكيب تشكل ذيلًا طويلًا يمينيًا في مخطط التوزيع. إذا استبعدنا 10٪ من التراكيب ونفذنا حسابات لـ 90٪ المتبقية من الحلول ، فسيكون وقت الحساب ( _يعني t90 _يعني ) أقل بكثير. على سبيل المثال ، بالنسبة للشطرنج 1000 × 1000 ، فإن متوسط ​​وقت العد سيكون 0.027727 ثانية ، أي أقل بمقدار 2.24 مرة من متوسط ​​الوقت الذي تم الحصول عليه من العينة بأكملها.

ج) بالنسبة للقيم رقم 800 ، في عينة التراكيب ، كانت هناك تلك التي لا يمكن استكمالها حتى حل كامل. هذا سلبي كاذبالحلول. ضمن الحدود المحددة في البرنامج ، مما يسمح بتنفيذ إجراء تتبع المسار حتى 1000 مرة ، فشلت الخوارزمية في إكمال هذه التراكيب. تم تصنيفها عن طريق الخطأ على أنها مؤلفات سلبية ، أي تلك التي ليس لديها حل. عدد مثل هذه الحلول السلبية الكاذبة ضئيلة ، وحصتها في العينة أقل من 0.0001. علاوة على ذلك ، مع زيادة n ، تنخفض نسبة الحلول السلبية الكاذبة . بالنسبة لجميع قيم n > 800 ، في هذه السلسلة من التجارب الحسابية ، لم تكن هناك حالة واحدة من الحلول السلبية الكاذبة . ومع ذلك ، فمن الواضح أنه إذا تم زيادة حجم العينة عدة مرات ، فلن يتم استبعاد احتمال ظهور False Negativeالحلول ، على الرغم من أن احتمال مثل هذا الحدث سيكون عددًا صغيرًا جدًا.

التعقيد الزمني للخوارزمية . يوضح الشكل 7 رسم بياني للتغيرات في متوسط ​​وقت الانتقاء للتركيبات العشوائية لقيم مختلفة من n .


التين. 7. اعتماد متوسط ​​وقت الانتقاء ( t ) للتركيبات العشوائية على حجم ( ن ) مصفوفة القرار. يتم

رسم اللوغاريتم العشري لقيمة n على محور abscissa ، ويتم رسم اللوغاريتم ، بزيادة 1000 مرة ، من متوسط ​​وقت العد ، على المحور الإحداثي. من أجل الوضوح ، يُظهر الشكل أيضًا الخط المنقط لرباعي الربع. يمكن ملاحظة أن وقت الالتقاط يزداد خطيًا مع زيادة في n. على كامل نطاق n من 50 إلى 10 ⁸تشكل القيم التجريبية لوقت العد خطًا مستقيمًا ، والذي يتم وصفه بدرجة ارتباط عالية إلى حد ما ( R = 0.9998 ) من خلال

سجل معادلة الانحدار الخطي (1000 * t) = - 0.628927 + 0.781568 * log (n)

الانحراف الطفيف عن الاتجاه العام نموذجي فقط للقيم n = ( 10 ، ... 49) ، والذي يرجع إلى حقيقة أنه يتم استخدام الكتلة الخامسة فقط من العمليات الحسابية في هذا النطاق لحل المشكلة ، حيث تختلف الخوارزمية اختلافًا كبيرًا عن تشغيل خوارزميات الكتل الأولى والثالثة. في التبعية الناتجة ، فإن المعامل الخطي ( 0.781568) أقل من الوحدة ، مما يؤدي إلى حقيقة أنه مع زيادة قيمة n ، فإن خط الانحدار والمائل للرباعي يتباعدان. من أجل توضيح سبب هذا التناقض بشكل واضح بدلاً من الوقت الأولي ، فإننا نعتبر متوسط ​​الوقت اللازم لموقع ملكة واحدة على سطر واحد ، أي اقسم متوسط ​​وقت العد على n . نحن نسمي هذا المؤشر بانخفاض الوقت . من الواضح ، إذا لم يتغير الوقت المنخفض مع زيادة n ، فسيكون مثل هذا الحل خطيًا ( O (n) ). كما رأينا في الشكل 8، حيث مؤامرة لوغاريتم وقت معين،


الشكل. 8 متوسط ​​وقت الاعتماد ( _الصف t) ، وهو أمر ضروري للملكة أن تكون موجودة على خط تعسفي واحد ، من حجم ( ن ) من مصفوفة الحل.

( tRow ) ، بزيادة 10 ⁶ مرات ، من لوغاريتم حجم مصفوفة الحل ، في حدود n من 50 إلى 10 ⁸ ، يتناقص الوقت المخفض بزيادة n . إذا كان الوقت المخفض لـ n = 50 هو 10.7146 * 10 ^-6 ثانية ، فسيتم تقليل الوقت المقابل لـ n = 10 ⁸ بمقدار 21 مرة ويكون 0.5084 * 10 ^-6ثواني. يبدو هذا السلوك للخوارزمية ، للوهلة الأولى ، خاطئًا ، حيث لا توجد أسباب موضوعية تجعل الخوارزمية تعتبرها أبطأ بالنسبة لقيم صغيرة من n مقارنة بالقيم الكبيرة. ومع ذلك ، لا يوجد أي خطأ ، وهذه خاصية موضوعية لهذه الخوارزمية. هذا يرجع إلى حقيقة أن هذه الخوارزمية عبارة عن تكوين من ثلاثة خوارزميات تعمل بسرعات مختلفة. علاوة على ذلك ، يتغير عدد الخطوط التي تتم معالجتها بواسطة كل من هذه الخوارزميات مع زيادة قيمة n. ولهذا السبب ، يزداد وقت العد في النطاق الأولي للقيم n = (10 ، 20 ، 30 ، 40) ، حيث يتم تنفيذ جميع العمليات الحسابية في هذه المساحة الصغيرة فقط على أساس مجموعة الإجراءات الخامسة ، والتي تعمل بكفاءة عالية ، ولكن ليس بالسرعة نفسها أول كتلة من الإجراءات. وبالتالي ، بالنظر إلى أن وقت العد المطلوب لوضع الملكة على سطر واحد ،يتناقص مع زيادة حجم رقعة الشطرنج ، يمكن تسمية التعقيد الزمني لهذه الخوارزمية بالتناقص.

عدد مرات استخدام تتبع الظهر (BT) . في جميع حالات التجربة الحسابية ، قمنا بتتبع عدد الحالات التي تستخدم إجراء BT في حل كل مشكلة. تم إجراء تجميع تراكمي لجميع حالات استخدام BT ، بغض النظر عن المستوى الأساسي الذي تم إرجاعه في عملية البحث عن حل. أعطانا هذا الفرصة لتحديد ، لكل عينة ، نسبة تلك القرارات التي لم يتم فيها استخدام إجراء BT. ويبين الشكل 9


الشكل. 9. نسبة القرارات في العينة التي لم يتم فيها استخدام إجراء تتبع المسار في

رسم بياني يوضح كيف تتغير نسبة حالات الحل دون استخدام إجراء BT ( Zero Back Tracking ) مع زيادة n. يمكن ملاحظة أنه في نطاق القيم n = (7 ، ... ، 100000) ، يتجاوز عدد الحلول التي لم يتم استخدام إجراء BT فيها 35٪. علاوة على ذلك ، في نطاق القيم n = (320 ، ... ، 22500) ، يتجاوز عدد هذه الحالات 50٪. وقد تم الحصول على معظم نتائج فعالة لحجم اللوحة 5000 x 5000 ، حيث، في عينة من 10000 التراكيب في 61.92٪ يؤديها الحالات "حتمية" القرار ليس حتمية مشكلة، لأن BT الإجراء في 61.92 ٪الحالات لم تستخدم قط. في الحلول المتبقية ، في 21.87 ٪ من الحالات ، تم استخدام الإجراء BT مرة واحدة ، في 9.07 ٪ من الحالات - 2 مرات ، و 3.77 ٪ من الحالات - 3 مرات. معا ، وهذا يمثل 96.63 ٪ من الحالات. حقيقة أنه بعد القيمة n = 5000 ، يتناقص تدريجياً عدد حالات حل مشكلة التكوين دون استخدام إجراء BT ، مع النموذج المحدد لتحديد القيم الحدية لـ baseLevel2 و baseLevel3 . يمكنك تغيير هذه المعلمات وتحقيق زيادة في عدد الحلول دون استخدام إجراء BT. ومع ذلك ، سيؤدي ذلك إلى زيادة في وقت الحساب ، حيث ستزيد مشاركة الكتلة الخامسة في تشغيل الخوارزمية.

الرسم البياني لتوزيع الوقت اختيار . في الشكل 10 ، بقيمة n = 1000يتم تقديم رسم بياني لتوزيع وقت الانتقاء لمليون حلول. لا يرتبط العرض غير العادي تمامًا لمخطط الرسم البياني للتوزيع (والذي يشبه على الأرجح صورة ظلية ليلية للمباني العالية) بخطأ في اختيار طول أو عدد الفواصل الزمنية. هذه خاصية طبيعية لهذه الخوارزمية. لفهم ،


التين. 10. رسم بياني لوقت تجميع التراكيب ذات الأحجام التعسفية. ( ن = 1000 ؛ حجم العينة = 1،000،000 )

لماذا يحتوي الرسم البياني على هذا النموذج ، ضع في اعتبارك توزيع وقت الانتقاء للتركيبات التي لها نفس الحجم. لهذا ، على سبيل المثال ، من العينة الأولية ، سنختار جميع التراكيب التي يبلغ حجمها 800. كان هناك 998 مثل هذه التراكيب في عينة من مليون. ويبين الشكل 11 رسم بياني لتوزيع وقت العد لهذه العينة. يمكن أن نرى من الشكل أن التوزيع يتكون من ستة رسوم بيانية منفصلة ، مع تناقص الأحجام.


التين. 11. رسم بياني لوقت تجميع التراكيب من نفس الحجم (ك = 800). ( ن = 1000 ؛ حجم العينة = 998 )

السبب في أن الوقت التجمع 998 المسارات في كل منها توزع 800 الملكات بشكل عشوائي، "عنقودية" إلى 6 مجموعات، هو استخدام الإجراء تتبع العودة. الرسم البياني الأول في الشكل ، مع الحد الأقصى لحجم العينة ، هو تلك الحلول المنتقاة حيث لم يتم استخدام إجراء BT مطلقًا. هذه مجموعة من أسرع الحلول. الرسم البياني الثاني ، وهو أصغر في الحجم من الأول ، هو تلك الحلول التي استخدم فيها إجراء BT مرة واحدة فقط. لذلك ، فإن وقت اتخاذ القرار في هذه المجموعة أطول بقليل من الوقت الأول. وفقًا لذلك ، في المجموعة الثالثة ، تم استخدام الإجراء BT مرتين ، في المجموعة الرابعة - ثلاث مرات ، وما إلى ذلك ، أي تم تنفيذ القرارات التي تم فيها استخدام إجراء BT مرارًا وتكرارًا على مدار فترة زمنية أطول. مثل هذه الحلول تشكل الذيل الأيمن الطويل للتوزيع المطلوب.

حلول سلبية كاذبة . إذا قمنا بتقسيم جميع التراكيب الممكنة على قيمة تعسفية لـ nإلى الإيجابية والسلبية ، ثم من بين التكوينات الإيجابية هناك تلك التي يمكن أن تصنفها هذه الخوارزمية على أنها سلبية. هذا يرجع إلى حقيقة أنه ضمن الحدود التي حددتها معلمات البحث ، لا يمكن للخوارزمية إيجاد الطريقة الصحيحة لإكمال هذه التراكيب. كما تظهر النتائج التجريبية (الجدول 2) ، لا يتجاوز عدد هذه الحالات 0.0001 من حجم العينة ، وتقل قيمة هذا الخطأ بزيادة n . بالإضافة إلى ذلك ، بالنسبة لجميع قيم n> 800 ، لم تكن هناك حالة واحدة من الحلول السلبية الكاذبة . حتى زيادة حجم العينة إلى مليون لـ n = 1000 لم ينتج عنه خطأ سالبالحلول. تسمح لنا النتيجة بصياغة القاعدة التالية لحل المشكلة: " يمكن إكمال أي تكوين عشوائي للملكات k يتم توزيعه باستمرار على رقعة الشطرنج التعسفية بالحجم nxn حتى يتم التوصل إلى حل كامل ، أو سيتقرر أن تكون هذه التركيبة سلبية ، ولا يمكن أن تكتمل. احتمال اتخاذ مثل هذا القرار لا يتجاوز 0.0001 . كلما زاد حجم رقعة الشطرنج ، تقل احتمالية اتخاذ القرارات الخاطئة. التعقيد الزمني للخوارزمية خطي. "

8. الاستنتاجات

1. يتم تقديم خوارزمية تسمح ، في الوقت الخطي ، بحل مشكلة المجموعة الكاملة حتى يتم حل كامل للتكوين العشوائي للملكات k ، ويتم توزيعه باستمرار على رقعة الشطرنج ذات الحجم التعسفي nxn . علاوة على ذلك ، بالنسبة لأي تركيبة للملكات k ( 1≤k <n ) ، يتم توفير حل ، إن وجد ، أو اتخاذ قرار بعدم اكتمال هذا التكوين. لا يتجاوز احتمال حدوث خطأ في اتخاذ مثل هذا القرار 0.0001 ، وتتناقص هذه القيمة مع زيادة حجم رقعة الشطرنج.

2. يعتمد تشغيل هذه الخوارزمية على استخدام قاعدتين مهمتين:

أ) في المرحلة الأخيرة من حل المشكلة ، من بين جميع الخطوط المجانية المتبقية ، يتم اختيار واحد يكون فيه عدد المراكز الحرة هو الحد الأدنى ( قاعدة المخاطرة الدنيا ). هذا يقلل من المخاطر المرتبطة بإمكانية استبعاد آخر المراكز الشاغرة في بعض الأسطر المتبقية.

ب) من بين جميع الوظائف الشاغرة في السطر المذكور ، يتم اختيار هذا الموضع الذي يسبب الحد الأدنى من الضرر للمواقع الحرة في الخطوط الحرة المتبقية ( قاعدة الحد الأدنى من الضرر ). يُقصد بعبارة " الحد الأدنى من الضرر " اختيار مثل هذا الموقف في خط يستثني أقل قدر من المراكز الحرة في جميع الخطوط المجانية المتبقية.

3. ثبت أنه نتيجة تشغيل هذه الخوارزمية ، يتناقص متوسط ​​الوقت اللازم لوضع الملكة على سطر واحد مع زيادة في قيمة n. متوسط ​​الوقت اللازم لوضع الملكة على سطر واحد في الحالة عندما يكون n 10 10 هو 21 مرة أقل من الوقت المقابل للحالة n = 50.

4. تم العثور على أنه في نطاق القيم n = (7 ، ... ، 100000) فإن عدد الحلول التي لم يتم استخدام إجراء التتبع السابق فيها يتجاوز 35٪. علاوة على ذلك ، في نطاق القيم n = (320 ، ... ، 22500) ، يتجاوز عدد هذه الحالات 50٪ ، مما يشير إلى الكفاءة العالية لهذه الخوارزمية.

5. يُقترح نموذج لتنظيم إجراء التتبع الخلفي ، استنادًا إلى تقسيم تسلسل خطوات القرار إلى مستويات أساسية. المستوى يعني خطوة قرار معينة مع وضع عدد معين من الملكات بشكل صحيح . يتم إعطاء صيغ الانحدار لحساب قيم المستوى الأساسي الثاني والثالث اعتمادًا على n .

6. يتم عرض نتائج التحليل المقارن لطريقتي اختيار عشوائي ، والتي تسمى randSet & randSet و rand & rand . تم العثور على خوارزمية randSet & randSet لتكون سريعة ، ولكن غير مهذب. لذلك ، يقتصر استخدامه عند الوصول إلى المستوى الأساسي الثاني. بعد ذلك ، يتم استخدام خوارزمية rand & rand ، وهي ليست بهذه السرعة ، ولكنها تضع الملكات بشكل أكثر كفاءة على رقعة الشطرنج.

7. يتم إعطاء خوارزمية فعالة للتحقق من صحة حل مشكلة n-Queens . تم تصميم هذا البرنامج أيضا للتحقق من صحة تكوين عشوائي من حجم التعسفي. البرنامج يعمل بسرعة كافية. على سبيل المثال ، الوقت اللازم للتحقق من صحة حل يتكون من 5 ملايين موضع هو 0.85 ثانية.

9. التعليقات

1. كما هو موضح في بداية المقال ، أجريت دراسات في نطاق قيم n ، من 7 إلى 100 مليون. ومع ذلك ، تم اختبار البرنامج في مجموعة واسعة من القيم ن ، ما يصل إلى مليار. صحيح ، في الحالة الأخيرة ، كان يجب تكييف البرنامج قليلاً ، بالنظر إلى الحجم الكبير للصفائف. لذلك ، إذا سمح حجم ذاكرة الوصول العشوائي (RAM) ، فمن الممكن إجراء عمليات حسابية لقيم كبيرة من n.

2. تم تحسين قيم المؤشرات الأساسية ، وكذلك القيم الحدية لعدد التكرارات على مختلف المستويات ، لحل المشكلة في نطاق البحث بأكمله. يمكن تغييرها في نطاق أصغر وتقليل وقت العد. من المهم عدم زيادة حصة الحلول السلبية الكاذبة .

3. في هذه المقالة ، استخدمت وقت الضغط على المفتاح Enter كمقياس للوقت لتقييم مدى سرعة الخوارزمية. إذا ظهرت النتيجة فورًا بعد الضغط على المفتاح ، فيبدو أن مستوى البرنامج "سريع جدًا" على مستوى إدراك المستخدم. بغض النظر عن سرعة عمل الخوارزمية ، لن تظهر النتيجة على الشاشة حتى يكتمل المفتاح. لذلك ، بدا لي أن مثل هذا المقياس المشروط للوقت يمكن أن يكون بمثابة مستوى عتبة لعدم المقارنة الصارمة بين سرعة الخوارزميات المختلفة.

4. الفلسفية ... خلال الدراسة ، تم النظر في عدد كبير من المنشورات المتعلقة بحل المشاكل غير القطعية. في معظم الحالات ، كانت هذه المهام التي كان من الضروري اتخاذ خيار في مساحة كبيرة من الدول في ظل ظروف قيود معينة. عند مقارنتها ، كان من المثير للاهتمام معرفة إلى أي مدى يمكن للمرء التقدم في حل هذه المشكلات باستخدام النهج الرياضي القياسي. لدي انطباع بأنه من المستحيل حل مثل هذه المشكلات فقط على أساس التعاريف وبيان الليمون وإثبات النظريات. يبدو لي أنه لحل مثل هذه المشكلات ، من الضروري استخدام أساليب الرياضيات الحسابية باستخدام محاكاة الكمبيوتر. لإثبات صحة هذا الاستنتاج ، على سبيل المثال البسيط ، قمت بإعداد لوحة رقعة الشطرنج ، حجمها 10 ⁹ × 10 ⁹ تركيبة من نفس الحجم ، تتكون من 999،999،482 ملكات. يتم إعدادها كما هو موضح في بداية المقالة ويتم تقديمها كملفين بتنسيق .mat. يمكن تنزيلها على هذا الرابط (ملفان للاختبار) . الملفات "ثقيلة" تمامًا ، يبلغ حجم كل منها حوالي 3.97 جيجابايت. في 999 997 976 سطرًا (في 99.9998٪ من الحالات) تتطابق مواقف الملكات في كلا التراكيبين ، وفقط في 1506 سطرًا تعسفيًا تختلف مواقف الملكات.

لإكمال بيانات التكوين إلى حل كامل ، تحتاج إلى وضع الملكات بشكل صحيح في الخطوط الحرة 518 المتبقية. يبلغ عدد الطرق الممكنة لترتيب 518 ملكات في الخطوط المجانية المتبقية (مع مراعاة فقط عدد طرق اختيار الموضع المجاني في السطر المحدد) حوالي 14 ¹⁴⁶⁶ . يتكون الفرق بين هذين التراكيبين فقط من حقيقة أن أحدهما إيجابي ويمكن إكماله حتى حل كامل ، والتكوين الآخر سلبي - لا يمكن إكماله حتى حل كامل. السؤال: "هل من الممكن ، على أساس مقاربة رياضية صارمة (أي دون إجراء عمليات حسابية حسابية) ، تحديد أي من هذين التراكيبين هو إيجابي؟" إذا كان هذا مستحيل الحل ، فيمكننا افتراض أن الاقتراح الذي تم تقديمه قد تم إثباته بالتناقض.

أريد أن أشير إلى أنه بغض النظر عن النهج المتبع في الحل الرياضي الدقيق لهذه المشكلة ، يحتاج المرء إلى تحديد حالة الخلايا 518 * 10 ⁹ في الخطوط الحرة المتبقية. للقيام بذلك ، من الضروري النظر في كل موقف للملكات المنشأة مسبقًا ، وهناك ما يقرب من مليار منهم لوضع القيود التي تفرضها كل ملكة قائمة على المواقف المجانية في الخطوط الـ 518 المتبقية. لم أجد "نقطة ارتكاز" من شأنها أن تسمح لي بالقيام بهذا العمل فقط على أساس نهج رياضي صارم ، دون حسابات حسابية.

لقد قدمت هنا مثالًا بسيطًا يتكون من مؤلفين فقط. إذا لزم الأمر ، يمكن زيادة عدد هذه التراكيب.

تجدر الإشارة إلى أنه على أساس الخوارزمية الخطية المقترحة ، والمكيفة قليلاً للعمل مع التراكيب الكبيرة ، يمكن إنجاز مهام أي من تركيبتي الاختبار قبل تنفيذ حل كامل على سطح المكتب 13 ، في حوالي 4.5 دقائق (باستثناء وقت التحميل إدخال البيانات).

10. إضافة

إن عمل الأساتذة الذين يوصون بالمهام القادرة للطلاب على التطوير والبحث يستحقون الاحترام. هذا يتطلب جهدا كبيرا ، ولكن التغلب على الصعوبات ، يبحث الباحث في المهام المعقدة الأخرى بشكل مختلف. اعتقدت أنه سيكون من المفيد توسيع خيارات إعداد مشكلة n-Queens لهذه الأغراض. إذا نظرت إلى نفس المهمة من وجهات نظر مختلفة ، يمكنك رؤية أشياء مختلفة. أدناه بعض منهم.

1. فكر في مشكلة ترتيب ملكات n على لوحة مستطيلة الشكل بحجم nxm . دلالة ك = م - ن . دع بعض الحلول يتم الحصول عليها ، وفي كل سطر من الأسطر n يجب أن توجد ملكة واحدة. نستبعد تلك المواقف التي توجد فيها ملكات من مزيد من الدراسة. الآن في كل سطر يوجد موقف m-1 مجاني. ضمن المواقف المجانية المتبقية ، نجد مرة أخرى حلاً واحدًا. كما كان من قبل ، نستبعد من النظر في المواقف التي توجد فيها ملكات الحل الثاني. الآن في كل صف هناك مواقف مجانية M-2 . من الواضح أن الحلول الأولى والثانية لا تتقاطع في مواقفها في أي صف - فهي متعامدة. يجب تحديد الحد الأقصى لعدد الحلول المتعامدة المتبادلة لقيم مختلفة من k . إذا تم إيجاد n حلول متعامدة متبادلة للقيمة k = 0 ، فسيتم بناء Royal Latin Square.

ملاحظة . أظهر Grigoryan E. (2018) أنه لأي حل لمشكلة n-Queens ، يوجد حل تكميلي لا يتقاطع معه. وهذا يعني أنه للحصول على قيمة تعسفية لـ n ، يتم تقسيم مجموعة حلول جميعها لمشكلة n-Queens إلى مجموعتين فرعيتين متساويتين في الحجم . أي حل من المجموعة الفرعية الثانية هو حل مكمل للحل المقابل من المجموعة الفرعية الأولى. القاعدة بسيطة للغاية ، إذا كانت Q1 (i) حلاً من المجموعة الأولى ، فسيتم تحديد الحل التكميلي المقابل Q2 (i) من المجموعة الفرعية الثانية بواسطة الصيغة Q2 (i) = n + 1 - Q1 (i) ، حيث i = (1 ، ... ، ن) . هذه هي القاعدة التي تشرح حقيقة أن عدد جميع الحلول لمشكلة n-Queens ، بالنسبة لقيمة n التعسفية ، دائمًا ما يكون رقمًا زوجيًا. (تسمح لنا هذه القاعدة بتخفيض وقت حساب جميع الحلول الكاملة إلى النصف الكامل للحجم التعسفي n من رقعة الشطرنج. إذا أشرنا بمقدار 2 * k إلى العدد الإجمالي لجميع الحلول ، فإن القيمة k تساوي الفهرس في القائمة التسلسلية لجميع الحلول عندما Q (k) + Q ( ك + 1) = ن + 1 ).

2. في الصياغة الأولية لمشكلة مشكلة n-Qeens ، بعد وضع الملكة في الموضع (i ، j) ، يتم تنفيذ الإجراءات التالية:

أ) استبعاد جميع خلايا الصف الأول والعمود ي

ب ) يتم استبعاد جميع الخلايا الموجودة على خط الأقطار اليسرى واليمنى التي تمر عبر الخلية (i، j) .

نغير الشرط ب) في بيان المشكلة. بدلا من القضاء على الخلايا ، سوف نستخدم تبديل الخلايا. إذا كانت الخلية الموجودة على خط الأقطار اليمنى أو اليسرى حرة ، فسنقوم بإغلاقها ؛ وإذا كانت الخلية مغلقة ، فسوف نفتتحها. هذا يجعل من السهل إيجاد حل. ومع ذلك ، بدلاً من المصفوفة المربعة nxn ، فإننا نعتبر مصفوفة مستطيلة من الحجم nx (n - k) . من المطلوب ، للحصول على قيمة معينة من n ، العثور على الحد الأقصى لقيمة k التي يمكن عندها الحصول على ثلاثة حلول متعامدة على الأقل. كيف ستتغير قيمة k مع زيادة قيمة n ؟

3. قم بتغيير بعض الشروط في الصيغة الأولية لمشكلة مشكلة n-Queens . عندما توضع الملكة في موضعها (i، j) على رقعة الشطرنج بحجم nxn :

أ) استبعاد جميع الخلايا في الصف الأول ،

ب) إذا كان الفهرس j هو رقم زوجي ، إذن:

b1) استبعاد الخلايا في صفوف الصفوف j ،

ب 2) نستبعد الخلايا حتى في الصفوف التي تتقاطع مع الأقطار اليسرى واليمنى التي تمر عبر الخلية (ط ، ي) ،

ج) إذا كان الفهرس j هو رقم فردي ، فإن النقطتين b1 و b2) تكون راضية عن الخلايا الموجودة في الصفوف الفردية.

3.1 من المعروف (Sloane-2016) أن قائمة قيم جميع حلول مشكلة nQueens ، لـ n = (8 ، 9 ، 10 ، 11 ، 12 ، 13 ، 14 ، 15 ، 16) ، على التوالي ، هي (92 ، 352 ، 724 ، 2680 ، 14200 ، 73712 ، 365596 ، 2279184 ، 14772512) . كيف سيتغير عدد الحلول إذا تم ، في بيان المشكلة ، تغيير الشرط القياسي للاستثناءات القطرية إلى الفقرة ب) أو الفقرة ج)؟

2.3 يعرف Grigoryan (2018) أننا إذا حددنا تواتر مشاركة خلايا مختلفة من مصفوفة الحلول في تشكيل قائمة بجميع الحلول ، يمكننا أن نجد أن هناك علاقات متناغمة بين جميع الخلايا في شكل تماثلات رأسية وأفقية للترددات المقابلة. هذا يعني أننا إذا افترضنا أن <k / n ، فإن تردد خلايا الصف k سيكون مطابقًا لترددات خلايا الصف n-k + 1 . وبالمثل ، سيكون تواتر خلايا العمود K-th مطابقًا لترددات خلايا العمود n-k + 1 . السؤال: كيف ستتغير هذه العلاقات المتناغمة في سياق المهمة؟

4. جميع خلايا رقعة الشطرنج تنقسم إلى فئتين حسب لونها. ويعتقد أن لون واحد أبيض ، والآخر أسود. فكر في ورقتي شطرنج وضع أحدهما على الآخر بحيث تتطابق الحواف تمامًا. نتيجة لذلك ، نحصل على "سندويش" من لوحين للشطرنج ، حيث يتزامن ترتيب الخلايا البيضاء والسوداء. تتمثل المهمة في إيجاد حلول في وقت واحد على لوحين ، مع مراعاة الشروط التالية:

أ) إذا كانت الملكة على إحدى اللوحات ، توجد على خلية سوداء بها مؤشرات (i ، j) ، إذن:

- في كلتا اللوحتين ، يتم استبعاد جميع الخلايا السوداء الموجودة في الصف الأول والعمود ي

- في كلتا اللوحتين ، يتم استبعاد جميع الخلايا السوداء الموجودة على طول الأقطار اليسرى واليمنى التي تمر عبر الخلية (i ، j) .

ب) إذا كانت الملكة على إحدى اللوحات ، تقع على خلية بيضاء مع الفهارس (i ، j) ، عندئذٍ يتم تنفيذ جميع الإجراءات الواردة في الفقرة (أ) فقط للخلايا البيضاء.

5. تخيل أنه في مصفوفة حل بحجم nxn ، يمكن أن تنزلق الصفوف بالنسبة إلى بعضها البعض إلى اليمين أو اليسار ، بخطوة من الخلايا k . علاوة على ذلك ، إذا تم نقل الصف السابق ، على سبيل المثال ، إلى اليسار ، فينبغي أن ينتقل الصف التالي إلى اليمين ، أي يتم تبديل كل سطر في الاتجاه المعاكس للخط السابق. نتيجة لهذا البناء ، نحصل على مصفوفة مستطيلة من الحجم nx (n + k) ، حيث سيتم في كل صف خلايا k من بداية الصف أو من النهاية استبعادها من الاعتبار. تتمثل المهمة في العثور على الحد الأقصى لقيمة k لقيمة عشوائية من n والتي يوجد لها حل واحد على الأقل مشكلة n-Queens .
ضع في اعتبارك متغير المشكلة التي يكون فيها إزاحة سطر واحد فيما يتعلق بخط آخر هو رقم عشوائي يتراوح من k1 إلى k2 .

6. الصياغة أحادية البعد لمشكلة nQueens . اسمح للقطاعات n ذات الطول التعسفي ، المرقمة من 1 إلى n ، بوضعها على نصف المحور. قسّم كل مقطع إلى خلايا n ذات حجم تعسفي ، وداخل كل قطعة ، قم بتعداد الخلايا من 1 إلى n . نحن نسمي هذه الخلايا مفتوحة. يجب إغلاق خلية واحدة في كل مقطع ، مع مراعاة القيود التالية:

أ) يمكننا اختيار خلية مفتوحة برقم j من الجزء i ، إذا:

D1 (r) = 0 ؛

D2 (t) = 0 ؛

حيث r = n + j - i و t = j + i و D1 و D2 عبارة عن صفائف تحكم أحادية البعد تتكون من 2n من الخلايا التي كانت صفراً في السابق.

ب) بعد هذا الاختيار ، سيتم إغلاق المقطع i والخلايا ذات الرقم j في جميع القطاعات المجانية المتبقية. من الضروري أيضًا إغلاق الخلايا المقابلة في صفيف التحكم:

D1 (ص) = 1 ؛

D2 (ر) = 1 ؛

في هذا الإعداد ، تكون المهمة مطابقة تمامًا للمهمة الأصلية. من المهم هو صياغة هذه المشكلة مع شروط القيد الأخرى. على سبيل المثال ، إذا بدلاً من الصيغ:
r = n + j - i ، t = j + i ،
سيتم النظر في العلاقات الأخرى التي تربط بين المؤشرات الوظيفية r و t بالمؤشرات (i، j) لمصفوفة القرار.

7. صياغة المهمة على أساس جرة مع الكرات (مماثلة للصياغة السابقة). دع هناك صناديق اقتراع مرقمة من 1 إلى ن ، وفي كل صندوق اقتراع توجد ن كرات ، مرقمة أيضًا من 1 إلى ن . يجب اختيار كرة واحدة من كل جرة ، مع مراعاة القيود التالية:

أ) يمكننا اختيار كرة برقم j من الظهور الثالث إذا:

D1 (ص) = 0 ،

D2 (ر) = 0 ،

حيث r = n + j - i و t = j + i و D1 و D2 عبارة عن صفائف تحكم أحادية البعد تتكون من 2n من الخلايا التي كانت صفراً في السابق.

ب) بعد هذا الاختيار ، سيتم إغلاق صندوق الاقتراع i والكرات بالرقم j في جميع صناديق الاقتراع المجانية المتبقية. من الضروري أيضًا إغلاق الخلايا المقابلة في صفيف التحكم:

D1 (ص) = 1 ،

D2 (ر) = 1 .

في هذا الإعداد ، تكون المهمة مطابقة تمامًا للمهمة الأصلية. كما في الحالة السابقة ، فإن بيان هذه المشكلة مع الشروط الأخرى التي تربط بين المؤشرات الوظيفية r و t وظيفيًا بالمؤشرات (i، j) لمصفوفة القرار أمر مهم.

8. اللعبة . النظر في رقعة الشطرنج من حجم nxn . دعنا نعيد اللون إلى الملكات ، دع بعض الملكات لها لون أبيض ، والبعض الآخر أسود. نعيد أيضًا اللون الأبيض والأسود المتناوب إلى خلايا رقعة الشطرنج ، بناءً على حقيقة أن الخلية ذات الفهرس (1 ، ن) يجب أن تكون بيضاء. جميع الخلايا في بداية اللعبة تعتبر مجانية. ملكات بيضاء تجعل الخطوة الأولى. يضع اللاعب الملكة في خلية تعسفية حرة مع مؤشرات (i، j) . فليكن خلية بيضاء. نتيجة لهذا الاختيار ، أغلق:

أ) جميع الخلايا البيضاء من الصف الأول ،

ب) جميع خلايا العمود الأبيض j ،

ج) جميع الخلايا البيضاء التي تقع على الأقطار اليسرى واليمنى التي تمر عبر الخلية (ط ، ي) .

إذا تبين أن الخلية (i ، j) سوداء ، فستكون جميع العناصر (أ ، ب ، ج) راضية ، وبناءً على ذلك ، تكون جميع الخلايا باللون الأسود مغلقة. بعد ذلك ، يقوم Black بالحركة ، بوضع الملكة في أي من الخلايا الحرة المتبقية. بعد ذلك ، بطريقة مماثلة ، تغلق الخلايا ، كما هو موضح أعلاه. يتم تحديد وقت التفكير في الخطوة التالية ، ويتم تحديده باتفاق الطرفين. إذا لم يكمل أحد اللاعبين خلال الوقت المحدد انتقاله ، يتم نقل اللعبة إلى اللاعب الآخر. تنتهي اللعبة إذا فشل اللاعبون ، واحد تلو الآخر ، في إكمال دورهم في الوقت المحدد. الشخص الذي يمكنه وضع المزيد من الملكات على السبورة يفوز.

9. على استقرار اختيار عشوائي. النظر في نموذج randSet و randSet .بمقارنة ن أزواج عشوائية من مؤشرات الصفوف والأعمدة للمرحلة الأولى من الدورة، فمن الممكن لتحديد ما معدله الملكات ك * ن الصفوف. يمكن اعتبار قيمة k قيمة ثابتة تساوي 0.6. تتراوح قيمتها من 0.605701 في n = 10 ، و 0.599777 ، في n = 10 ⁶ ، ومع زيادة n ، ينخفض ​​التباين في هذه القيمة. ما هو سبب هذا "الثبات"؟ لماذا ، مع اختيار عشوائي لمؤشر الصفوف ومؤشر موضع الملكة في هذا الصف ، على أساس قائمتين من الأرقام التي تم الحصول عليها على أساس التقليب العشوائي للأرقام من 1 إلى n ، هل من الممكن وضع الملكات باستمرار (في المتوسط) على 60 ٪ من الخطوط؟

10. دع حجم رقعة الشطرنج متساويةnxn . استنادًا إلى إجراء randSet & randSet ، نضع الملكات على رقعة الشطرنج حتى يصل فرع البحث إلى طريق مسدود. تشير إلى طول التكوين التي حصلت عليها ك . إذا ، لقيمة معينة من n ، كررت هذا الإجراء عدة مرات ، وقمت بإنشاء رسم بياني لتوزيع قيم k ، ثم اتضح أن التغيير في وتيرة حدوث الأحداث إلى قيمة وضع التوزيع يختلف عن التغيير في تواتر حدوث الأحداث بعد هذه القيمة. إذا تم تقسيم الرسم البياني ، استنادًا إلى القيمة الوسيطة ، إلى جزأين ، فلن يتزامن الجزء الأيسر مع الجزء الأيمن. هذا النمط مميز لأي قيمة لـ n. لماذا ، بعد انتقال طول التكوين خلال القيمة الوسيطة ، هل يتخذ تواتر الأحداث شكلًا مختلفًا؟ نعني بالحصول على تكوين بحجم معين ، قبل الوصول إلى حالة من الجمود.

أدب

1. ناوك ، ف. (1850). Briefwechsel mit allen fur alle . Illustrierte Zeitung، 15، 182.

2. Gent، IP، Jefferson، C. & Nightingale ، ص (2017). تعقيد إتمام n-Queens ،
مجلة أبحاث الذكاء الاصطناعي ، 59 ، 815-848.

3. Sosic، R.، & Gu، J. (1990). خوارزمية وقت متعدد الحدود لمشكلة n-queens . نشرة SIGART ، 1 (3) ، 7-11.

4. ريتشاردز ، م (1997). التراجع عن الخوارزميات في MCPL باستخدام أنماط البت والتكرار .
التكنولوجيا. ممثل ، مختبر الحاسوب ، جامعة كامبريدج.

5. أساليب التوزيع العشوائي في تصميم الخوارزمية، وقائع ورشة عمل DIMACS ، برينستون ، نيو جيرسي ، الولايات المتحدة الأمريكية ، 12-14 ديسمبر 1997. سلسلة DIMACS في الرياضيات المنفصلة وعلوم الكمبيوتر النظرية 43 ، DIMACS / AMS 1999 ، ردمك 978-0-8218-0916-7

6. غريغوريان E. (2018). دراسة الاشتقاقات في تشكيل مشكلة n-Queens . نمذجة الذكاء الاصطناعي ، 5 (1) ، 3-21.

7. Sloane N.-JA (2016). الموسوعة على الإنترنت من تسلسل عدد صحيح.