غالبًا ما تحتوي الجداول على عدد كبير من الحقول المنطقية ، ولا توجد طريقة لفهرستها كلها ، وفعالية هذا الفهرسة منخفضة. ومع ذلك ، للعمل مع التعبيرات المنطقية التعسفية في SQL ، فإن آلية الفهرسة متعددة الأبعاد مناسبة ، والتي سيتم مناقشتها تحت القط.
في SQL ، يتم استخدام الحقول المنطقية بشكل أساسي في حالتين. أولاً ، عندما تحتاج حقًا إلى سمة ثنائية ، على سبيل المثال ، "شراء / بيع" في جدول المعاملات. هذه الصفات نادرا ما تتغير مع مرور الوقت.
ثانياً ، تسجيل
حالة جهاز الحالة الذي يصف السجل. من المفهوم أن الكائن المنطقي المقابل لإدخال الجدول يمر عبر سلسلة من الحالات ، يتم تحديد عددها والانتقالات بينها حسب المنطق المطبق. مثال بسيط هو تقنية "الحذف الناعم" ، عندما لا يتم إتلاف السجل ماديًا ، ولكن يتم تمييزه فقط على أنه محذوف.
إذا كانت الآلة معقدة ، يمكن أن يكون هناك قدر لا بأس به من هذه الحقول ، في أحد طاولاتنا هناك 58 (+14 قديمة) مثل هذه الحقول (بما في ذلك مجموعات العلم) وهذا ليس شيئًا غير طبيعي. لم يكن هذا مخططًا له في الأصل ، ولكن مع تطور المنتج وتغيير المتطلبات الخارجية ، يتم تطوير الآلات ذات الصلة ، ويأتي المطورون ويذهبون ، ويتغير المحللون ... في مرحلة ما قد يكون الحصول على علامة جديدة أكثر أمانًا ، بدلاً من فهم جميع التعقيدات. علاوة على ذلك ، تراكمت البيانات التاريخية ويجب أن تظل ظروفها كافية.
offtopicيشبه هذا في بعض النواحي العملية التطورية ، عندما يتم تخزين كتلة من المعلومات / الآليات في الجينوم ، والتي لا تكون هناك حاجة للوهلة الأولى على الإطلاق ، لكن من المستحيل التخلص منها. من ناحية أخرى ، يجدر التعامل مع هذه الآليات باحترام ، لأنها هي التي مكنت أسلاف التطور من البقاء (بما في ذلك خلال
الانقراض الكبير ) والفوز بالسباق التطوري. مرة أخرى ، من يدري إلى أين سيقودنا التطور وما الذي سيكون مفيدًا في المستقبل.
لا يعني وضع علامة إضافة حقل من النوع المقابل فحسب ، بل أيضًا أخذه في الاعتبار في تشغيل التشغيل التلقائي ، وما يوضحه ، وفي أي انتقالات يشارك فيها. في الممارسة العملية ، يبدو مثل هذا:
- عملية أو سلسلة من العمليات ، دعنا نسميها "كتاب" ، وإنشاء سجلات جديدة في الحالة الأولية (ربما في واحدة من الحالات الأولية)
- في عدد من العمليات ، دعنا نسميها "القراء" ، من وقت لآخر يقرؤون الكائنات الموجودة في الحالات التي يحتاجون إليها
- عددًا من العمليات ، دعنا نسميها "معالجات" ، ومراقبة حالات معينة ، وتغيير هذه الحالات بناءً على المنطق المطبق. أي تشغيل آلة الدولة.
لتحديد السجلات الموجودة في حالة معينة ، يكون من النادر أن تكفي عملية التصفية بواسطة أحد الحقول المنطقية. عادة ما يكون هذا تعبيرًا تامًا ، أحيانًا غير تافه. يبدو أنك تحتاج إلى فهرسة هذه الحقول وسيقوم معالج SQL بتحديدها. لكن ليس بهذه البساطة.
أولاً ، يمكن أن يكون هناك العديد من الحقول المنطقية ؛ فهرستها جميعًا سيكون هدرًا للغاية.
ثانياً ، قد يتحول الأمر إلى فائدة منذ ذلك الحين ستكون الانتقائية لكل حقل منخفضة ، ولا تتم تغطية احتمالات المفصل بواسطة إحصائيات معالج SQL.
افترض أنه يوجد في الجدول T1 حقلان منطقيان: F1 & F2 ، والاستعلام
select F1, F2, count(1) from T1 group by F1, F2
يعطيه
أي على الرغم من أن F1 و F2 ، صحيح وصحيح محتمل بنفس الدرجة ، فإن المجموعة (صواب ، خطأ) لا تسقط إلا مرة واحدة من أصل ألف. نتيجة لذلك ، إذا فهرست F1 و F2 بشكل منفصل وأجبرنا
على استخدامها في الاستعلام ، فسيتعين على معالج SQL قراءة نصف الفهارس وتجاوز النتائج. قد يكون أرخص قراءة الجدول بأكمله وحساب التعبير لكل سطر.
وحتى إذا قمت بجمع إحصاءات حول الطلبات المكتملة ، فلن يكون لها فائدة كبيرة. الإحصاءات على وجه التحديد للحقول المسؤولة عن حالة الجهاز تطفو كثيرا. في الواقع ، في أي لحظة قد يأتي "معالج" وينقل نصف الخطوط من الحالة S1 إلى S2.
للعمل مع مثل هذه التعبيرات ، يقترح الفهرس متعدد الأبعاد نفسه ، وقد تم
تقديم خوارزمية في
وقت سابق وثبت أنها جيدة للغاية.
ولكن عليك أولاً معرفة كيف سيتحول تعبير منطقي تعسفي إلى استعلام (طلبات) للفهرس.
شكل عادي طباشيري
استعلام واحد إلى فهرس متعدد الأبعاد هو مستطيل متعدد الأبعاد يحد من مساحة الاستعلام. إذا شارك الحقل في الطلب ، فسيتم تعيين قيود عليه. إذا لم يكن الأمر كذلك ، فإن المستطيل في هذا الإحداثي يقتصر فقط على عرض هذا الإحداثي. الإحداثيات المنطقية لها قدرة 1.
استعلام البحث في هذا الفهرس عبارة عن سلسلة من & (بالتزامن) ، على سبيل المثال ، التعبير: v1 & v2 & v3 & (! V4) ، أي ما يعادل v1: [1،1] ، v2: [1،1] ، v3: [1 ، 1] ، الإصدار 4: [0،0]. وجميع الحقول الأخرى لها نطاق: [0،1].
بالنظر إلى هذا ، تتحول نظراتنا على الفور إلى
DNF - أحد الأشكال المتعارف عليها للتعبيرات المنطقية. يقال إن أي تعبير يمكن تمثيله على أنه انفصال عن الاقتران الأدبي. يشير الحرفي هنا إلى حقل منطقي أو نفيه.
وبعبارة أخرى ، من خلال التلاعب البسيط ، يمكن تمثيل أي تعبير منطقي باعتباره انفصالًا عن عدة استعلامات إلى فهرس منطقي متعدد الأبعاد.
هناك واحد ولكن. مثل هذا التحول في بعض الحالات يمكن أن يؤدي إلى زيادة كبيرة في حجم التعبير. على سبيل المثال ، التحويل من
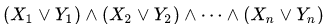
يؤدي إلى تعبير عن مصطلحات ** **. في مثل هذه الحالات ، يجب على مطور التطبيق التفكير في المعنى المادي لما يفعله ، ومن جانب معالج SQL ، يمكنك دائمًا رفض استخدام الفهرس المنطقي إذا تجاوز عدد الإضافات الحدود المعقولة.
خوارزمية الفهرسة متعددة الأبعاد
بالنسبة للفهرسة متعددة الأبعاد ، يتم استخدام خصائص منحنى الترقيم المتشابه ذاتياً القائم على البساطات الفائقة التكعيب مع الجانب 2. كما
اتضح فيما بعد ، فإن إصدارين من هذه المنحنيات لهما أهمية عملية - منحنى Z- ومنحنى Hilbert.
 الشكل 1 الشكل 2. ثنائي الأبعاد منحنى Z ، 3 و 6 التكرارات
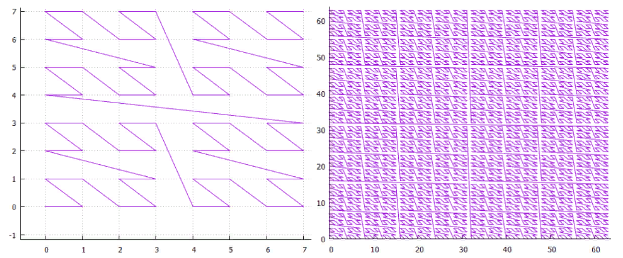
الشكل 1 الشكل 2. ثنائي الأبعاد منحنى Z ، 3 و 6 التكرارات الشكل 2 الشكل 2. ثنائي الأبعاد منحنى هيلبرت ، 3 و 6 التكرارات
الشكل 2 الشكل 2. ثنائي الأبعاد منحنى هيلبرت ، 3 و 6 التكرارات- يحتوي البسيط N-dimensional ذو الجانب 2 على نقطتين ** n و 2 (n ** 1) انتقالات بينهما.
- يحول التكرار الأولي للبسيطة كل رأس من البساطة إلى أبسط مستوى منخفض.
- بعد القيام بالعدد اللازم من التكرارات ، يمكننا إنشاء شبكة مفرطة التكعيب من أي حجم.
- بالإضافة إلى ذلك ، سيكون لكل عقدة من هذه الشبكة رقم فريد خاص بها - المسار الذي تم اتخاذه على طول منحنى الترقيم من بدايته. علاوة على ذلك ، كل عقدة من هذه الشبكة لها قيمة في كل من الإحداثيات. في الواقع ، يقوم منحنى الترقيم بترجمة النقطة متعددة الأبعاد إلى قيمة أحادية البعد مناسبة للفهرسة باستخدام شجرة B منتظمة .
- جميع العقد الموجودة داخل simplex من أي مستوى تقع ضمن نفس الفاصل الزمني ولا يتقاطع هذا الفاصل مع أي simplex من نفس المستوى.
- لذلك ، يمكن تقسيم أي مستطيل بحث (مربع) إلى عدد صغير من الاستعلامات الفرعية شديدة التكعيب ، يمكن في كل منها قراءة الفهرس بواسطة بحث / اجتياز واحد.
- نضيف إلى هذا سحر العمل المنخفض المستوى مع شجرة B لكي لا نطلب طلبات غير مجدية و ... الخوارزمية جاهزة.
إليك كيف تعمل في الممارسة:
 الشكل 3 مثال على البحث في فهرس ثنائي الأبعاد (منحنى Z)
الشكل 3 مثال على البحث في فهرس ثنائي الأبعاد (منحنى Z)يوضح الشكل 3 تقسيم نطاق البحث الأصلي إلى استعلامات فرعية والنقاط التي تم العثور عليها. تم استخدام فهرس ثنائي الأبعاد ، تم بناؤه على مجموعة عشوائية موزعة بشكل موحد من 100000000 نقطة [1،000،000 ، 1،000،000].
مؤشر متعدد الأبعاد المنطقي
نظرًا لأننا نتحدث عن الفهرسة متعددة الأبعاد ، فقد حان الوقت للتفكير في مقدار الأبعاد المتعددة التي يمكن أن تكون؟ هل هناك أي قيود موضوعية؟
بالطبع ، نظرًا لأن B-tree بها تنظيم صفحة ولكي تكون شجرة ، يجب ضمان عنصرين على الأقل لتناسبهما في الصفحة. إذا كنت تأخذ الصفحة ل 8 K ، ثم تخزين عنصر واحد لا يمكن أن يذهب أكثر من 4K. في 4K ، بدون ضغط ، يتم احتواء حوالي 1000 قيمة من 32 بت. هذا كثير جدًا ، وبخلاف حدود أي تطبيق معقول ، يمكننا القول أن الحدود المادية غير متوفرة عملياً.
هناك جانب آخر ، كل بُعد إضافي ليس مجانيًا على الإطلاق ، فهو يشغل مساحة على القرص ويبطئ العمل. من وجهة نظر "المعنى المادي" ، ينبغي إدراج الحقول التي تتغير في نفس الوقت في نفس الفهرس والبحث يسير أيضًا. لا يوجد أي نقطة في فهرسة كل شيء على التوالي.
الحقول المنطقية مختلفة. كما رأينا ، يمكن أن تشارك عشرات من المجالات المنطقية في نفس الآليات. وتكاليف التخزين / القراءة صغيرة جدًا. هناك إغراء لجمع جميع الحقول المنطقية في فهرس واحد ومعرفة ما يحدث.
صحيح ، هناك فروق دقيقة:
- حتى الآن ، في القيمة المفهرسة ، كانت أرقام الإحداثيات المختلفة مختلطة ، وكانت الأرقام الأقل أهمية في المفتاح أقل البتات أهمية من الإحداثيات ... لذلك ، لم يكن ترتيب الحقول أثناء الفهرسة مهمًا.
- الآن ، يتم إنفاق جزء واحد على تخزين قيمة حقل منطقي واحد. أي ستنتقل بعض الحقول المنطقية إلى نهاية المفتاح ، والبعض الآخر إلى البداية. هذا يعني أن التصفية حسب جزء من الحقول ستكون فعالة للغاية ، والبعض الآخر سيكون غير فعال للغاية. في الواقع ، إذا قمنا بالبحث بالترتيب الأدنى ، فسوف يتعين علينا قراءة الفهرس بالكامل للحصول على إجابة. لكن هذا (على الأرجح) أفضل من قراءة الجدول بأكمله للإجابة على نفس السؤال.
- هناك مشكلة في الاختيار - جميع الحقول المنطقية متساوية ، لكن بعضها سيكون أكثر مساواة من الحقول الأخرى. من الاعتبارات العامة ، من الضروري النظر إلى تشوهات الإحصاءات ، فكلما كانت النسبة الحقيقية / الخاطئة لحقل معين بعيدة عن التوازن ، يجب أن يكون الأقدم هو التفريغ الذي تظهر به قيمته.
- يختفي التقسيم حسب نوع منحنى الترقيم ، إذا كان من الضروري في وقت سابق الاختيار بين منحنى Z ومنحنى Hilbert ، فلا يوجد فرق عملي في البيانات أحادية البت.
- NULL-ق. استنادًا إلى حقيقة أن NULL ليست قيمة غير معروفة ، ولكن مع عدم وجود أي قيمة ، لا ينبغي إدراج هذه السجلات في الفهرس. في المؤشرات أحادية البعد ، هذا ما يحدث. لكن في حالتنا ، قد يتضح أن بعض الحقول المنطقية تحتوي على قيم ، وبعضها لا يحتوي على قيم. نتيجة لذلك ، لا يمكننا وضع هذا في الفهرس منذ ذلك الحين خوارزمية البحث لا تعرف كيفية العمل مع المنطق الثلاثي. وبالتالي ، يجب أن يكون من المستحيل إدراج هذه السجلات في الجدول (إذا كان هناك فهرس متعدد الأبعاد ، وليس بالضرورة منطقيًا ، بالمناسبة)
من المتوقع أن لا يعمل فهرس منطقي متعدد الأبعاد في بعض الحالات بكفاءة عالية. بالمعنى الدقيق للكلمة ، يمكن أن يعمل أي فهرس بطريقة غير فعالة إذا وقع الكثير من البيانات في منطقة البحث. لكن بالنسبة للفهرس المنطقي متعدد الأبعاد ، يتفاقم هذا بسبب الاعتماد على ترتيب الحقل الموصوف أعلاه ، عندما يكون عليك قراءة الفهرس بأكمله من أجل نتيجة صغيرة. بقدر ما هذه مشكلة في الممارسة العملية ، يمكن أن تظهر التجربة فقط.
التجربة العددية
بناء فهرس:
- سيكون الفهرس 128 بت ، أي بنيت على 128 المجالات المنطقية
- وسوف تحتوي على 2 ** 30 عنصر
- ستكون قيمة عنصر الفهرس رقمًا من 0 إلى 2 ** 30
- سيكون مفتاح عنصر الفهرس هو نفس الرقم الذي تم تحويله 48 بت إلى اليسار ، أي سيتم تعبئة الحقول المنطقية من 48 إلى 78 بأرقام الرقم بنفس الترتيب
- نتيجة لذلك ، حصلنا على 30 حقلًا منطقيًا مهمًا في منتصف المفتاح ، وسيتم ملء البتات المتبقية 0
- كل حقل منطقي به إحصائيات متساوية صح / خطأ
- كلها مستقلة إحصائيا.
بحث:
- تقابل كل تجربة اختيار عدة مجالات منطقية متتالية وتعيين قيم البحث لها. ليس لأن الخوارزمية يمكنها البحث فقط في خطوط ، ولكن نظرًا لأنه من الممكن تصور نتائج التجربة بشكل أكثر وضوحًا ، فلدينا بعدان فقط - عرض الشريط وموضعه
- ما مجموعه 24 سلسلة من التجارب. في كل سلسلة ، سوف نبحث عن القيم التي يأخذ فيها شريط الحقول المنطقية للعرض المقابل N (من 1 إلى 24 بت) القيمة الحقيقية.
- في كل سلسلة سيكون هناك مجموعات فرعية من التجارب التي يوجد فيها شريط من الحقول المنطقية ذات العرض المحدد مع التحولات المختلفة S من بداية الشريط إلى 30 مجال منطقي مهم. مجموع (30-N) التجارب في فرعية.
- في كل تجربة ، يتم البحث عن جميع عناصر الفهرس التي تفي بالشرط ، أي سيتم البحث في الحقول ذات الأرقام في الفاصل الزمني [48 + S ، 48 + S + N -1] في الفاصل الزمني [1،1] ، والباقي في الفاصل الزمني [0،1]
- يتم البحث من البداية الباردة
- والنتيجة هي عدد صفحات القرص التي تمت قراءتها ، بما في ذلك التخزين المؤقت (4096 صفحة في ذاكرة التخزين المؤقت)
- يتم التحكم في العملية الصحيحة بطريقتين - يجب أن يكون عدد العناصر الموجودة يساوي 2 ** (30-N) وفي القيم الموجودة يمكنك التحقق من الأرقام المقابلة
وهكذا،
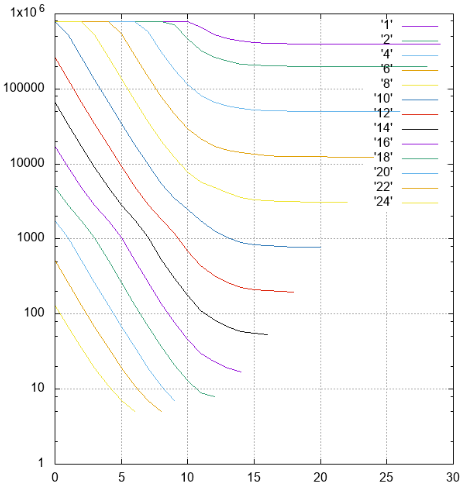 الشكل 4 النتائج ، وعدد الصفحات قراءة في سلسلة مختلفة
الشكل 4 النتائج ، وعدد الصفحات قراءة في سلسلة مختلفةبواسطة Y - تم تأجيل عدد صفحات القراءة.
على X - تحول الشرائح من الفئة الأصغر (48) إلى الأقدم. يتم توقيع خطوط بعرض مختلف وتمييزها بألوان مختلفة.
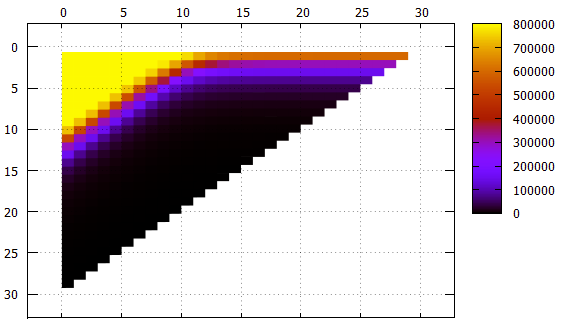 الشكل 5 نفس البيانات كما الشكل 4 ، وجهة نظر أخرى
الشكل 5 نفس البيانات كما الشكل 4 ، وجهة نظر أخرىX - الفرقة التحول
Y - عرض النطاق الترددي
ما يجب ملاحظته:
- على الرغم من أن هذا غير مرئي بشكل مباشر في الصور ، إلا أن الفهرس يعمل بشكل صحيح ، إلا أنه مرئي في عدد العناصر التي تم العثور عليها وفي محتوى العناصر نفسها
- تتطلب كل الخطوط التي لا يزيد عرضها عن 10 مع إزاحة 0 قراءة مستمرة للفهرس
- المشارب بعرض 1 إلى 18 مع زيادة في التحول تصل إلى الخط المقرب 2 ** (- N) من حجم الفهرس بأكمله ، وهو منطقي
- بالنسبة إلى النطاقات الأوسع للخط المقارب - ارتفاع الشجرة ، لا يمكن أن يكون هناك قراءات أقل
- يتم وضع أكثر من 1000 عنصر في صفحة ورقة الفهرس ، ويمكن ملاحظة ذلك في شريط بعرض 10 ، والذي عند التحول 0 لم يعد يتطلب قراءة الفهرس بأكمله ، يمكن تخطي بعض الصفحات
- تصفية المستوى المنخفض يعمل بشكل جيد بشكل مدهش. ضع في اعتبارك شريطًا ذي عرض 10. يكون خيار البحث المثالي هو إزاحة 20 (أي ما مجموعه 30 حقلًا مهمًا) ، عندما لا توجد حقول غير محددة في البادئة على الإطلاق ، يمكن العثور على البيانات باستخدام حزمة واحدة. في هذه الحالة ، تتم قراءة حوالي 1/1000 من الفهرس أثناء البحث - 779 صفحة.
الحالة المتوسطة عبارة عن تحول 10 ، ولدينا بادئة ولاحقة من 10 حقول غير معروفة. عدد الصفحات 2484 ، أسوأ بثلاث مرات فقط من الحالة المثالية.
وحتى في أسوأ الحالات ، مع تحول 0 (بادئة 20 حقلًا غير معروف) ، يمكنك تخطي بعض الصفحات.
بشكل عام ، يمكن التعرف على خوارزمية الفهرسة متعددة الأبعاد على أنها فعالة حتى في مثل هذه الحالة السخيفة.
ولكن يعتبر الخيار الأكثر نجاحًا من وجهة نظر الفهرس المنطقي - حالات متساوية في جميع المجالات المنطقية المستقلة.تجربة على البيانات الحقيقية
جدول
الصفقات ، إجمالي 278،479،918 صفًا ، بيانات من إحدى حلقات الاختبار.
نتائج بعض الاستعلامات في الجدول أدناه:
تستغرق قراءة / معالجة صفحة واحدة في المتوسط 0.8 مللي ثانية.
ليست هناك حاجة لوصف معنى استفسارات محددة ، فهي موجودة هنا فقط لإثبات قابلية التشغيل. والتي ، بالمناسبة ، أكد.
ولكن قبل أن تكون هذه التقنية ذات فائدة عملية ، لا يزال هناك الكثير مما يجب عمله. لذلك ، أن تستمر.