🍵 🥑 👨🏻‍🎓 التعزيز العميق التعلم: كيفية تعليم العناكب على المشي 🙅🏿 👩🏽‍🏫 😦

اليوم سوف أخبرك كيف طبقت خوارزميات التعلم العميق للتحكم في الروبوت. باختصار ، سوف أخبرك بكيفية إنشاء "مربع أسود مع شبكات عصبية" ، والذي يقبل بنية الروبوت عند الإدخال وينتج خوارزمية يمكنها التحكم فيه في المخرجات.

جوهر الحل هو خوارزمية Advantage Actor Cror (A2C) مع عشرات Advantage من خلال تقدير المزايا العامة (GAE).

تحت الخفض ، والرياضيات ، وتطبيق TensorFlow ، والكثير من العروض التوضيحية لأي نوع من خوارزميات المشي جاءت إليه.

المحتويات:

- التحدي
- لماذا تعزيز التعلم؟
- بيان التعلم التعزيز
- التدرج السياسة
- السياسات الغوسية القطرية
- تقليل التباين عن طريق إضافة النقد
- مطبات

- الخاتمة

مهمة

في هذه المقالة ، سوف نعلم الروبوت على السير في محاكاة MuJoCo. سنقوم بتخطي وصف الخطوة بإنشاء نموذج للروبوت وواجهة Python للبيئة ، لأن لا يوجد شيء مثير للاهتمام هناك. لفهم ، انظر فقط إلى العروض التجريبية في MuJoCo نفسها ومصادر بيئات MuJoCo في Gym OpenAI .

عند الإدخال ، سيكون للوكيل أرقام عديدة من MuJoCo: المواضع النسبية وزوايا الدوران والسرعة وتسريع أجزاء جسم الروبوت ، إلخ. في المجموع ، ترتيب ~ 800 الميزات. نحن نستخدم نهج التعلم العميق ولن نفهم ما يعنيه في الواقع. الشيء الرئيسي هو أنه في هذه المجموعة من الأرقام ستكون هناك معلومات كافية بحيث يمكن للعميل أن يفهم ما يحدث له.

في الخرج ، نتوقع 18 رقمًا - عدد درجات حرية الروبوت ، مما يعني زوايا دوران المفصلات التي تم تثبيت الأطراف عليها.

أخيرًا ، هدف الوكيل هو زيادة المكافأة الكلية للحلقة. سننهي الحلقة إذا تعطل الروبوت أو إذا مرت 3000 خطوة (15 ثانية). كل خطوة سوف تكافئ الوكيل وفقًا للمعادلة التالية:

$\ newcommand {\ E} {\ mathop {\ mathbb {E}}} \ newcommand {\ R} {\ mathop {\ mathbb {R}}} r_t = \ Delta x * 1000 + 0.5$

أي هدف الوكيل سيزيد من تنسيقه $x$ ولا تسقط حتى نهاية الحلقة.

لذلك ، تم تعيين المهمة: للعثور على وظيفة $\ pi: \ R ^ {800} \ to \ R ^ {18}$ التي المكافأة عن الحلقة سيكون أعظم . هذا لا يبدو صحيحا جدا؟ :) دعونا نرى كيف يعالج التعلم العميق العميق هذه المهمة.

لماذا التعلم التعزيز؟

تتكون الأساليب الحديثة لحل مشكلة حركة الروبوتات المشي من ممارسات الروبوتات الكلاسيكية من أقسام التحكم الأمثل وتحسين المسار : LQR ، QP ، والتحديث المحدب. اقرأ المزيد: نشر فريق Boston Dynamics على نظام Atlas .

هذه التقنيات هي نوع من "القرص الصلب" لأنها تتطلب إدخال العديد من تفاصيل المهمة مباشرة في خوارزمية التحكم. لا توجد أنظمة تعلم فيها - يتم التحسين "على الفور".

من ناحية أخرى ، لا يتطلب تعزيز التعلم (يشار إليه فيما يلي RL) فرضيات في الخوارزمية ، مما يجعل حل المشكلة أكثر عمومية وقابلية للتطوير.

بيان التعلم التعزيز

مصدر

في مشكلة RL ، نعتبر تفاعل العامل والبيئة كسلسلة من الأزواج (الحالة والمكافأة) والانتقالات بينهما - الفعل .

$(s_0) \ xrightarrow {a_0} (s_1، r_1) \ xrightarrow {a_ {1}} ... \ xrightarrow {a_ {n-1}} (s_n، r_n)$

تحديد المصطلحات:

$\ pi (a_t | s_t)$ - السياسة ، استراتيجية سلوك الوكيل ، الاحتمال المشروط ،
$a_t \ sim \ pi (\ cdot | s_t)$ - يعتبر الإجراء متغير عشوائي من التوزيع $\ pi$ .
يمكن أن نعتبر السياسة وظيفة $\ pi: الولايات \ إلى الإجراءات$ ، ولكننا نريد أن نجعل العوامل العشوائية ، والتي تسهل الاستكشاف . أي مع بعض الاحتمالات فإننا لا نقوم بالإجراءات التي يختارها الوكيل.
$\ tau$ - مسار تتبع من قبل وكيل ، تسلسل $(s_1 ، s_2 ، ... ، s_n)$ .

مهمة الوكيل هي زيادة العائد المتوقع :

$J (\ pi) = \ E _ {\ tau \ sim \ pi} [R (\ tau)] = \ E _ {\ tau \ sim \ pi} \ left [\ sum_ {t = 0} ^ n r_t \ right ]$

الآن يمكننا صياغة مشكلة RL ، العثور على:

$\ pi ^ * = arg \ mathop {max} _ \ pi J (\ pi)$

حيث $\ pi ^ *$ هي السياسة المثلى.

اقرأ المزيد في المادة من OpenAI: OpenAI Spinning Up .

تدرج السياسة

تجدر الإشارة إلى أن البيان الدقيق لمشكلة RL كمشكلة تحسين يمنحنا الفرصة لاستخدام أساليب التحسين المعروفة بالفعل ، على سبيل المثال ، نزول التدرج . فقط تخيل كم سيكون رائعًا إذا استطعنا أخذ تدرج العائد المتوقع من خلال معلمات النموذج : $\ nabla_ \ theta J (\ pi_ \ theta)$ . في هذه الحالة ، ستكون قاعدة تحديث المقاييس بسيطة:

$\ theta = \ theta_ {old} + \ alpha \ nabla_ \ theta J (\ pi_ \ theta)$

هذه هي بالتحديد فكرة جميع أساليب التدرج السياسي . الاستنتاج الدقيق لهذا التدرج هو المتشددين إلى حد ما. لن نكتبها هنا ، ولكن نترك رابطًا للمواد الرائعة من OpenAI . التدرج يشبه هذا:

$\ nabla_ \ theta J (\ pi_ \ theta) = \ E _ {\ tau \ sim \ pi_ \ theta} \ left [\ sum_ {t = 0} ^ T \ nabla_ \ theta \ log \ pi_ \ theta (a_t | s_t) R (\ tau) \ right]$

وبالتالي ، فإن فقدان نموذجنا سيكون مثل هذا:

$خسارة $ = - \ log (\ pi_ \ theta (a_t | s_t)) R (\ tau) $$

أذكر ذلك $R (\ tau) = \ sum_ {t = 0} ^ T r_t$ و $\ pi_ \ theta (a_t | s_t)$ - هذا هو ناتج نموذجنا في الوقت الذي كانت فيه $s_t$ . ظهر الطرح بسبب حقيقة أننا نريد تعظيم $J$ . أثناء التدريب ، سننظر في التدرج على الدُفعات وإضافتها من أجل تقليل التباين (ضوضاء البيانات بسبب البيئة العشوائية).

هذه خوارزمية تعمل تسمى REINFORCE . وهو يعرف كيفية إيجاد حلول لبعض البيئات البسيطة. على سبيل المثال ، "CartPole-v1" .

النظر في رمز الوكيل:

class ActorNetworkDiscrete: def __init__(self): self.state_ph = tf.placeholder(tf.float32, shape=[None, observation_space]) l1 = tf.layers.dense(self.state_ph, units=20, activation=tf.nn.relu) output_linear = tf.layers.dense(l1, units=action_space) output = tf.nn.softmax(output_linear) self.action_op = tf.squeeze(tf.multinomial(logits=output_linear,num_samples=1), axis=1) # Training output_log = tf.nn.log_softmax(output_linear) self.weight_ph = tf.placeholder(shape=[None], dtype=tf.float32) self.action_ph = tf.placeholder(shape=[None], dtype=tf.int32) action_one_hot = tf.one_hot(self.action_ph, action_space) responsible_output_log = tf.reduce_sum(output_log * action_one_hot, axis=1) self.loss = -tf.reduce_mean(responsible_output_log * self.weight_ph) optimizer = tf.train.AdamOptimizer(learning_rate=actor_learning_rate) self.update_op = optimizer.minimize(self.loss) actor = ActorNetworkDiscrete()

لدينا مدرك صغير لهذه البنية: (obsation_space ، 10 ، action_space) [بالنسبة لـ CartPole هذا هو (4 ، 10 ، 2)]. tf.multinomial يسمح لك باختيار إجراء مرجح عشوائيًا. للحصول على إجراء تحتاج إلى الاتصال به:

 action = sess.run(actor.action_op, feed_dict={actor.state_ph: observation})

ولذا فإننا سوف ندربه:

 batch_generator = generate_batch(environments, batch_size=batch_size) for epoch in tqdm_notebook(range(epochs_number)): batch = next(batch_generator) # Remainder: batch item consists of [state, action, total reward] # Train actor _, actor_loss = sess.run([actor.update_op, actor.loss], feed_dict={actor.state_ph: batch[:, 0], actor.action_ph: batch[:, 1], actor.weight_ph: batch[:, 2]})

يدير مولد الدُفعات العامل في البيئة ويجمع البيانات للتدريب. عناصر الدفعة هي tuples من هذا النوع: $(s_t ، a_t ، R (\ tau))$ .

تعد كتابة مولد جيد مهمة منفصلة ، حيث تتمثل الصعوبة الرئيسية في التكلفة العالية النسبية للاتصال sess.run () مقارنة بخطوة محاكاة واحدة (حتى MuJoCo). لتسريع العمل ، يمكنك استغلال حقيقة أن الشبكات العصبية تعمل على دفعات ، وتستخدم العديد من البيئات المتوازية. حتى إطلاقها بالتسلسل في موضوع واحد سيعطي تسارع كبير مقارنة ببيئة واحدة.

رمز المولد باستخدام DummyVecEnv من خطوط الأساس OpenAI

 # Vectorized environments with gym-like interface from baselines.common.vec_env.subproc_vec_env import SubprocVecEnv from baselines.common.vec_env.dummy_vec_env import DummyVecEnv def make_env(env_id, seed): def _f(): env = gym.make(env_name) env.reset() # Desync environments for i in range(int(200 * seed // environments_count)): env.step(env.action_space.sample()) return env return _f envs = [make_env(env_name, seed) for seed in range(environments_count)] # Can be switched to SubprocVecEnv to parallelize on cores # (for computationally heavy envs) envs = DummyVecEnv(envs) # Source: # https://github.com/openai/spinningup/blob/master/spinup/algos/ppo/core.py def discount_cumsum(x, coef): """ magic from rllab for computing discounted cumulative sums of vectors. input: vector x, [x0, x1, x2] output: [x0 + discount * x1 + discount^2 * x2, x1 + discount * x2, x2] """ return scipy.signal.lfilter([1], [1, float(-coef)], x[::-1], axis=0)[::-1] def generate_batch(envs, batch_size, replay_buffer_size): envs_number = envs.num_envs observations = [[0 for i in range(observation_space)] for i in range(envs_number)] # [state, action, discounted reward-to-go] replay_buffer = np.empty((0,3), np.float32) # [state, action, reward] rollout lists for every environment instance rollouts = [np.empty((0, 3)) for i in range(envs_number)] while True: history = {'reward': [], 'max_action': []} replay_buffer = replay_buffer[batch_size:] # Main sampling cycle while len(replay_buffer) < replay_buffer_size: # Here policy acts in environments. Note that it chooses actions for all # environments in one batch, therefore expensive sess.run is called once. actions = sess.run(actor.action_op, feed_dict={actor.state_ph: observations}) observations_old = observations observations, rewards, dones, _ = envs.step(actions) history['max_action'].append(np.abs(actions).max()) time_point = np.array(list(zip(observations_old, actions, rewards))) for i in range(envs_number): # Regular python-like append rollouts[i] = np.append(rollouts[i], [time_point[i]], axis=0) # Process done==True environments if dones.all(): print('WARNING: envs are in sync!! This makes sampling inefficient!') done_indexes = np.arange(envs_number)[dones] for i in done_indexes: rewards_trajectory = rollouts[i][:, 2].copy() history['reward'].append(rewards_trajectory.sum()) rollouts[i][:, 2] = discount_cumsum(rewards_trajectory, coef=discount_factor) replay_buffer = np.append(replay_buffer, rollouts[i], axis=0) rollouts[i] = np.empty((0, 3)) # Shuffle before yield to become closer to iid np.random.shuffle(replay_buffer) # Truncate replay_buffer to get the most relevant feedback from environment replay_buffer = replay_buffer[:replay_buffer_size] yield replay_buffer[:batch_size], history # Make a test yield a = generate_batch(envs, 8, 64) # Makes them of equal lenght for i in range(10): next(a) next(a)[0]

يمكن للعامل الناتج اللعب في بيئات ذات مساحة محدودة من الإجراءات . هذا التنسيق غير مناسب لمهمتنا. يجب على الوكيل الذي يتحكم في الروبوت إصدار متجه من $\ R ^ n$ حيث $ن$ - عدد درجات الحرية. ( أو يمكنك تقسيم مساحة الإجراء إلى فجوات والحصول على مهمة باستخدام إخراج منفصل )

السياسات الغوسية القطرية

يتمثل جوهر نهج السياسات الغوسية القطرية في أن ينتج النموذج معلمات للتوزيع الطبيعي للأبعاد n ، وهي: $\ mu_ \ theta$ - حصيرة. الانتظار و $\ sigma_ \ theta$ - الانحراف المعياري. بمجرد أن يحتاج الوكيل إلى اتخاذ إجراء ، سنطلب هذه المعلمات من النموذج واتخاذ متغير عشوائي من هذا التوزيع. لذلك جعلنا خروج الوكيل $\ R ^ n$ وجعلها مؤشر ستوكاستيك. الشيء الأكثر أهمية هو أنه بعد إصلاح فئة التوزيع في الإخراج ، يمكننا حساب $\ log (\ pi_ \ theta (a_t | s_t))$ وبالتالي سياسة التدرج.

ملاحظة: يمكن أن تكون ثابتة $\ sigma_ \ theta$ كما hyperparameter ، وبالتالي تقليل البعد الناتج. تبين الممارسة أن هذا لا يسبب الكثير من الضرر ، ولكن على العكس من ذلك ، يستقر في التعلم.

اقرأ المزيد عن سياسة الاستوكاستك .

رمز الوكيل:

 epsilon = 1e-8 def gaussian_loglikelihood(x, mu, log_std): pre_sum = -0.5 * (((x - mu) / (tf.exp(log_std) + epsilon))**2 + 2 * log_std + np.log(2 * np.pi)) return tf.reduce_sum(pre_sum, axis=1) class ActorNetworkContinuous: def __init__(self): self.state_ph = tf.placeholder(tf.float32, shape=[None, observation_space]) l1 = tf.layers.dense(self.state_ph, units=100, activation=tf.nn.tanh) l2 = tf.layers.dense(l1, units=50, activation=tf.nn.tanh) l3 = tf.layers.dense(l2, units=25, activation=tf.nn.tanh) mu = tf.layers.dense(l3, units=action_space) log_std = tf.get_variable(name='log_std', initializer=-0.5 * np.ones(action_space, std = tf.exp(log_std) self.action_op = mu + tf.random.normal(shape=tf.shape(mu)) * std # Training self.weight_ph = tf.placeholder(shape=[None], dtype=tf.float32) self.action_ph = tf.placeholder(shape=[None, action_space], dtype=tf.float32) action_logprob = gaussian_loglikelihood(self.action_ph, mu, log_std) self.loss = -tf.reduce_mean(action_logprob * self.weight_ph) optimizer = tf.train.AdamOptimizer(learning_rate=actor_learning_rate) self.update_op = optimizer.minimize(self.loss)

الجزء التدريب لا يختلف.

الآن يمكننا أن نرى في النهاية كيف ستعمل REINFORCE على التعامل مع مهمتنا. فيما يلي ، هدف الوكيل هو الانتقال إلى اليمين.

ببطء ولكن بثبات نحو هدفه.

مكافأة للذهاب

لاحظ أن هناك أعضاء إضافيين في التدرج لدينا. وهي لكل خطوة $t$ عندما نزن التدرج اللوغاريتم ، نستخدم المكافأة الكلية للمسار بأكمله . وبالتالي ، تقييم تصرفات الوكيل بإنجازاته من الماضي. يبدو خطأ ، أليس كذلك؟ لذلك هذا

$\ nabla_ \ theta J (\ pi_ \ theta) = \ E _ {\ tau \ sim \ pi_ \ theta} \ left [\ sum_ {t = 0} ^ T \ nabla_ \ theta \ log \ pi_ \ theta (a_t | s_t) \ sum_ {t '= 0} ^ T r_ {t'} \ right]$

سوف تصبح هذا

$\ nabla_ \ theta J (\ pi_ \ theta) = \ E _ {\ tau \ sim \ pi_ \ theta} \ left [\ sum_ {t = 0} ^ T \ nabla_ \ theta \ log \ pi_ \ theta (a_t | s_t) \ sum_ {t '= t} ^ T r_ {t'} \ right]$

البحث عن 10 الاختلافات :)

في حين أن وجود هؤلاء الأعضاء لا يفسد أي شيء رياضيا ، إلا أنه يسبب الكثير من الضوضاء لنا. الآن ، أثناء التدريب ، سوف يهتم الوكيل فقط بالمكافآت التي تلقاها بعد إجراء محدد .

بسبب هذا التحسن ، نمت المكافأة المتوسطة. أحد الوكلاء الذين تلقوا تعلمت استخدام forelimbs لتحقيق هدفه:

تقليل التباين عن طريق إضافة النقد

جوهر التحسينات الإضافية هو تقليل الضوضاء (التباين) الناجم عن التحولات العشوائية بين حالات الوسط.

سيساعدنا ذلك على إضافة نموذج يتنبأ بمتوسط مقدار المكافآت التي يتلقاها الوكيل ، بدءًا من الحالة $s$ في نهاية المسار ، أي وظيفة القيمة.

$V ^ \ pi (s) = \ E _ {\ tau \ sim \ pi} \ left [R (\ tau) | s_0 = s \ right] \ text {- دالة القيمة}$

$Q ^ \ pi (s، a) = \ E _ {\ tau \ sim \ pi} \ left [R (\ tau) | s_0 = s ، a_0 = a \ right] \ text {- وظيفة الإجراء-القيمة}$

$A ^ \ pi (s، a) = Q ^ \ pi (s، a) -V ^ \ pi (s) \ text {- Advantage function}$

تُظهر وظيفة القيمة العائد المتوقع إذا كانت سياستنا تبدأ اللعبة من حالة معينة. الشيء نفسه مع Q- وظيفة ، فقط إصلاح أول إجراء.

إضافة النقد

هذه هي الطريقة التي يظهر بها التدرج اللوني عند استخدام المكافأة:

$\ nabla_ \ theta \ log \ pi_ \ theta (a_t | s_t) \ sum_ {t '= t} ^ T r_ {t'}$

الآن معامل التدرج اللوغاريتم ليس أكثر من عينة من دالة القيمة.

$\ sum_ {t '= t} ^ T r_ {t'} \ sim V ^ \ pi (s_t)$

نحن نزن التدرج اللوغاريتم بعينة واحدة من مسار معين ، وهو أمر غير جيد. يمكننا تقريب دالة القيمة مع بعض النماذج ، على سبيل المثال ، شبكة عصبية ، ونطلب القيمة اللازمة منها ، وبالتالي تقليل التباين. سوف نسمي هذا النموذج بالناقد (الناقد) وسندرسه بالتوازي مع السياسة. وبالتالي ، يمكن كتابة صيغة التدرج على النحو التالي:

$\ nabla_ \ theta \ log \ pi_ \ theta (a_t | s_t) \ sum_ {t '= t} ^ T r_ {t'} \ approx \ nabla_ \ theta \ log \ pi_ \ theta (a_t | s_t) V ^ \ pi (\ tau)$

لقد قمنا بتقليل التباين ، ولكن في الوقت نفسه ، أدخلنا التحيز في خوارزمية لدينا ، لأن الشبكات العصبية يمكن أن تحدث أخطاء تقريبية. لكن الحل الوسط في هذه الحالة جيد. وتسمى هذه الحالات في التعلم الآلي المفاضلة التحيز .

سيقوم الناقد بتدريس انحدار القيمة في عينات المكافآت التي يتم جمعها في البيئة. كدالة خطأ ، نأخذ MSE. أي الخسارة تبدو مثل هذا:

$loss = ({V} ^ \ pi_ \ psi (s_t) - \ sum_ {t '= t} ^ T r_ {t'}) ^ 2$

كود الناقد:

 class CriticNetwork: def __init__(self): self.state_ph = tf.placeholder(tf.float32, shape=[None, observation_space]) l1 = tf.layers.dense(self.state_ph, units=100, activation=tf.nn.tanh) l2 = tf.layers.dense(l1, units=50, activation=tf.nn.tanh) l3 = tf.layers.dense(l2, units=25, activation=tf.nn.tanh) output = tf.layers.dense(l3, units=1) self.value_op = tf.squeeze(output, axis=-1) # Training self.value_ph = tf.placeholder(shape=[None], dtype=tf.float32) self.loss = tf.losses.mean_squared_error(self.value_ph, self.value_op) optimizer = tf.train.AdamOptimizer(learning_rate=critic_learning_rate) self.update_op = optimizer.minimize(self.loss)

تبدو دورة التدريب الآن كالتالي:

 batch_generator = generate_batch(envs, batch_size=batch_size) for epoch in tqdm_notebook(range(epochs_number)): batch = next(batch_generator) # Remainder: batch item consists of [state, action, value, reward-to-go] # Train actor _, actor_loss = sess.run([actor.update_op, actor.loss], feed_dict={actor.state_ph: batch[:, 0], actor.action_ph: batch[:, 1], actor.weight_ph: batch[:, 2]}) # Train critic for j in range(10): _, critic_loss = sess.run([critic.update_op, critic.loss], feed_dict={critic.state_ph: batch[:, 0], critic.value_ph: batch[:, 3]})

تحتوي الدُفعة الآن على قيمة ، قيمة أخرى ، يتم حسابها بواسطة الناقد في المولد.
أي نوع الدفعة هو هذا: $(s_t، a_t، V ^ \ pi_ \ psi (s_t)، \ sum_ {t '= t} ^ T r_ {t'})$ .

في الدورة ، لا يوجد شيء يحدنا من تدريب الناقد على التقارب ، لذلك نحن نأخذ عدة خطوات من نزول التدرج ، وبالتالي تحسين تقريب وظيفة القيمة وتقليل الانحياز. ومع ذلك ، يتطلب هذا الأسلوب حجم دفعي كبير لتجنب إعادة التدريب. بيان مماثل حول سياسة التعلم غير صحيح. يجب أن تحتوي على تعليقات فورية من بيئة التعلم ، وإلا فقد نجد أنفسنا في موقف حيث نقوم بضبط سياسة الإجراءات التي لم تكن قد اتخذتها بالفعل. تسمى الخوارزميات مع هذه الخاصية على السياسة .

خطوط الأساس في التدرجات السياسية

يمكن أن يُظهر أنه في التدرج ، يجوز وضع فئة واسعة من الوظائف المفيدة الأخرى $t$ . وتسمى هذه الوظائف خطوط الأساس . ( استنتاج هذه الحقيقة ) الوظائف التالية تؤدي بشكل جيد خطوط الأساس:

المصدر: ورقة GAE .

تعطي خطوط الأساس المختلفة نتائج مختلفة حسب المهمة. كقاعدة عامة ، يتم الحصول على أكبر ربح من خلال ميزة Advantage وتقريبها.

هناك حدس بسيط وراء ذلك. عندما نستخدم Advantage ، نقوم بفرض غرامة على الوكيل بما يتناسب مع مدى أفضل أو أسوأ من المتوسط الذي يعتبره العامل في الإجراء الذي قام به. وكلما كان العامل يلعب دورًا أفضل في البيئة ، أصبحت معاييره أعلى . سوف يلعب العامل المثالي أداءً جيدًا ويقيِّم جميع تصرفاته على أنه يحتوي على ميزة تساوي 0 ، وبالتالي ، يكون معامل التدرج يساوي 0.

تقييم ميزة من خلال وظيفة القيمة

أذكر تعريف الميزة:

$A ^ \ pi (s، a) = Q ^ \ pi (s، a) -V ^ \ pi (s) \ text {- Advantage function}$

ليس من الواضح كيفية تعلم هذه الوظيفة بشكل صريح. سوف يتم توفير خدعة ، مما يقلل من حساب وظيفة Advantage إلى حساب وظيفة القيمة.

حدد $\ delta_t ^ V = r_t + V (s_ {t + 1}) - V (s_t)$ - الفرق الزمني المتبقي ( TD- المتبقية ). ليس من الصعب استنتاج أن هذه الوظيفة تقارب المزايا:

$\ E \ left [\ delta ^ V_t \ right] = \ E \ left [r_t + V (s_ {t + 1}) - V (s_t) \ right] = \ E \ left [Q (s_t، a_t) -V (s_t) \ right] = A (s_t ، a_t)$

مثل هذا التغيير المعقد من الناحية النظرية يثير تغييرا غير كبير في الكود. الآن ، بدلاً من تقييم وظيفة القيمة ، سيقدم الناقد تقييم ميزة للتدريب على السياسة.

تسمى الخوارزمية الناتجة Advantage Actor-Critic .

 def estimate_advantage(states, rewards): values = sess.run(critic.value_op, feed_dict={critic.state_ph: states}) deltas = rewards - values deltas = deltas + np.append(values[1:], np.array([0])) return deltas, values

يمكن ملاحظة العوامل التي تم الحصول عليها مشية واثقة واستخدام متزامن للأطراف:

تقدير الميزة العامة

تقدم مقالة حديثة نسبيًا (2018) ، " التحكم المستمر عالي الأبعاد باستخدام تقدير الميزة العامة " ، تقييمًا أكثر فعالية للميزة من خلال وظيفة القيمة. يقلل من التباين أكثر:

$A_t ^ {GAE (\ gamma، \ lambda)} = \ sum_ {l = 0} ^ \ infty (\ gamma \ lambda) ^ l \ delta ^ V_ {t + l}$

حيث:

$\ delta_t ^ V = r_t + V (s_ {t + 1}) - V (s_t)$ - TD المتبقية ،
$\ gamma$ - عامل الخصم (hyperparameter) ،
$\ lambda$ - hyperparameter.

يمكن العثور على التفسير في المنشور نفسه.

التنفيذ:

 def discount_cumsum(x, coef): # Source: # https://github.com/openai/spinningup/blob/master/spinup/algos/ppo/core.py """ magic from rllab for computing discounted cumulative sums of vectors. input: vector x, [x0, x1, x2] output: [x0 + discount * x1 + discount^2 * x2, x1 + discount * x2, x2] """ return scipy.signal.lfilter([1], [1, float(-coef)], x[::-1], axis=0)[::-1] def estimate_advantage(states, rewards): values = sess.run(critic.value_op, feed_dict={critic.state_ph: states}) deltas = rewards - values deltas = deltas + discount_factor * np.append(values[1:], np.array([0])) advantage = discount_cumsum(deltas, coef=lambda_factor * discount_factor) return advantage, values

عند استخدام حجم دفعة صغيرة ، تقاربت الخوارزمية مع بعض أوبتيما المحلية. هنا ، يستخدم الوكيل مخلبًا واحدًا كقصب ، والباقي يدفع:

هنا ، لم يأت العامل باستخدام القفزات ، ولكن ببساطة بالإصبع بسرعة مع أطرافه. ويمكنك أيضًا رؤية كيف يتصرف ، إذا كان مترددًا ، فسوف يستدير ويواصل الركض:

أفضل عميل ، هو في بداية المقال. القفز المستقر ، حيث تنطلق جميع الأطراف من السطح. تتيح القدرة المطورة للتوازن للوكيل تصحيح المسار بأقصى سرعة إذا حدث خطأ:

المزالق

يشتهر التعلم الآلي ببعد مساحة الأخطاء التي يمكن ارتكابها والحصول على خوارزمية لا تعمل بشكل كامل. لكن RL تنقل المشكلة إلى مستوى جديد تمامًا.

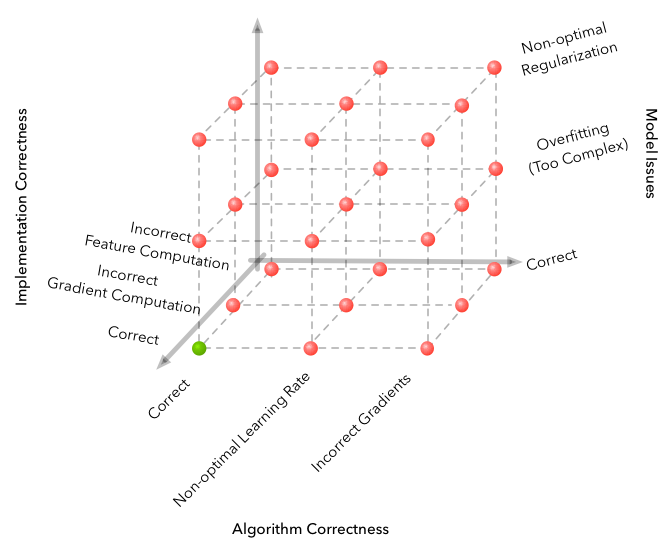
مصدر

فيما يلي بعض الصعوبات التي واجهتها أثناء التطوير.

الخوارزمية حساسة بشكل مثير للدهشة للمعايير الفوقية. كان هناك تغيير في جودة التعلم عند تغيير معدل التعلم من 3e-4 إلى 1e-4. تغيرت الصورة بشكل جذري - من خوارزمية غير متقاربة تمامًا إلى الأفضل في الفيديو.
لا يختلف حجم الدُفعة على الإطلاق كما هو الحال في مناطق DL الأخرى. إذا سمحت لنفسك في تصنيف الصور باختيار حجم الدُفعة 32-256 ولن تتغير النتيجة بشكل خاص من زيادتها ، فمن الأفضل أن تأخذ بضعة آلاف ، 3000 يعمل لمهمتنا ، ومرة أخرى من عدم التقارب إلى خوارزمية جيدة.
من الأفضل أن يتم التعلم عدة مرات ، وأحيانًا لا يكون الحظ محظوظًا.
يستغرق التعلم في مثل هذه البيئة المعقدة الكثير من الوقت والتقدم غير منتظم. على سبيل المثال ، أفضل خوارزمية تعلمت لمدة 8 ساعات ، 3 منها أظهرت نتيجة أسوأ من خط الأساس العشوائي. لذلك ، عند اختبار الخوارزميات ، من الأفضل أن تبدأ بواحدة صغيرة ، مثل بيئات الألعاب من صالة الألعاب الرياضية.
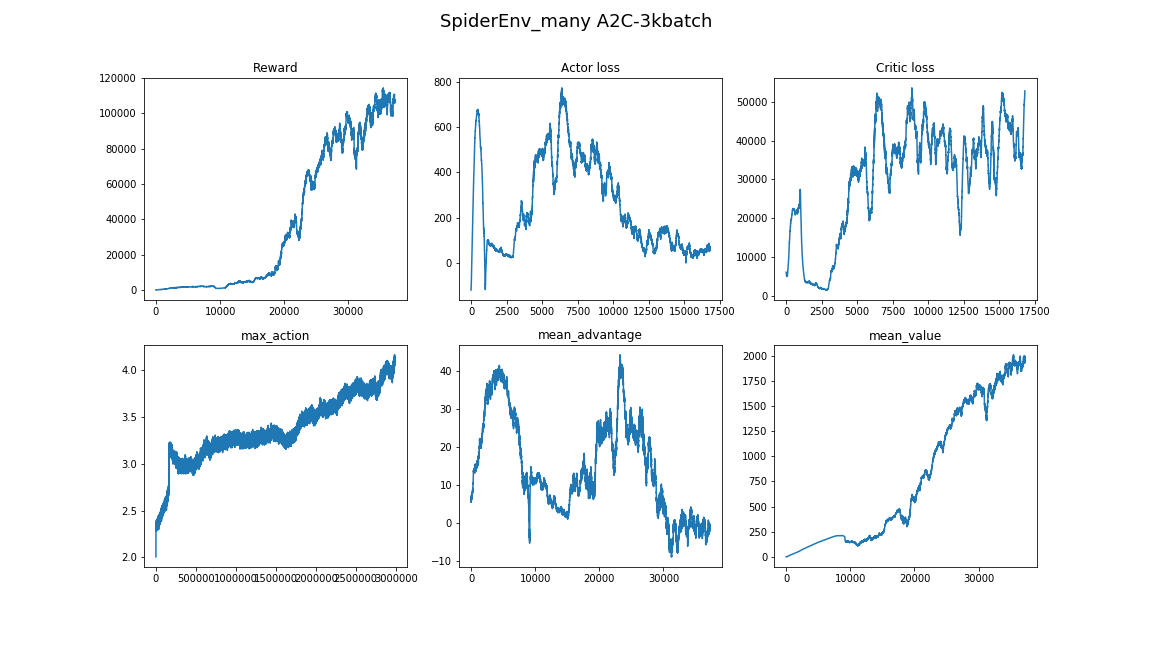
من المقاربات الجيدة لإيجاد المقاييس الفوقية وهندسة النماذج أن تدقق في المقالات والتطبيقات ذات الصلة. (الشيء الرئيسي هو عدم إعادة تدريب)

يمكنك معرفة المزيد عن الفروق الدقيقة في Deep RL من هذه المقالة: التعلم العميق لتعزيز لا يعمل حتى الآن .

استنتاج

الخوارزمية الناتجة تحل المشكلة بشكل مقنع. وظيفة وجدت $\ pi: \ R ^ {800} \ to \ R ^ {18}$ ، رشيق وثقة السيطرة على الروبوت.

وستكون الاستمرارية المنطقية هي دراسة أقارب خوارزميات A2C و PPO و TRPO. أنها تحسن كفاءة العينة ، أي وقت التقارب للخوارزمية ، وهم قادرون على حل مشاكل أكثر تعقيدًا. كان PPO + Automatic Domain Randomization هو الذي جمع مؤخرًا روبيك كيوب على روبوت .

هنا يمكنك العثور على الكود من المقال: مستودع .

أتمنى أن تكون قد استمتعت بالمقال واستلهمت من ما يمكن أن يفعله التعلم العميق الداعم اليوم.

شكرا لاهتمامكم!

روابط مفيدة:

بفضل pinkotter و Vambala و andrey_probochkin و pollyfom و suriknik للمساعدة في المشروع.
على وجه الخصوص ، Vambala andrey_probochkin لخلق بيئة رائعة MuJoCo.

التعزيز العميق التعلم: كيفية تعليم العناكب على المشي