عد المجتمع "ماذا؟" إلى أين؟ متى؟ "(ChGK) أو كم عدد المصافحات أمام صديق؟

مرحبا يا هبر!

عطلة رأس السنة الجديدة هي وقت كبير ل تأخذ استراحة من ذلك استخدام المهارات المهنية في هوايتك المفضلة. بالالتفاف على موقع تصنيف ChGK الرياضي ، وجدت واجهة برمجة تطبيقات ممتازة تتيح لك الحصول على بيانات عن جميع الألعاب في جميع البطولات. لذلك حصلت على فكرة بناء رسم بياني لمجتمع الخبراء واختبار نظرية ستة مصافحات على مجتمع مشتت جغرافيا وغير متصل بدقة. تحت صور الكاتوم من الرسوم البيانية والإحصاءات عديمة الفائدة.

بادئ ذي بدء ، برنامج تعليمي موجز ، ما هو الرياضة ChGK.

استرجاع البيانات

نفترض أن اللاعبين على دراية ببعضهم البعض إذا لعبوا مرة واحدة على الأقل على طاولة لعبة واحدة. بفضل واجهة برمجة التطبيقات الجيدة ، لا يمثل تنزيل البيانات المتعلقة بجميع البطولات وجميع الفرق مشكلة.

تحت المفسدين ، ولا يستخدم حتى حساء جميل ، يطلب فقط. سيكون في نهاية المقال دفتر ملاحظات للمشتري مع كل شفرة المصدر.

url = 'https://rating.chgk.info/api/tournaments.json/?page={}' df = pd.DataFrame(columns=['name', 'start']) for i in range(1, 7): data = requests.get(url.format(i)).json() for item in data["items"]: df.loc[item["idtournament"]] = (item["name"], item["date_start"]) df.to_csv('tournaments.csv') 

يبقى تنزيل قوائم الألعاب لجميع البطولات وتذكر جميع المعارف. في البداية ، خططت لتخزين حقائق لعبة مشتركة في DataFrame ، لكن سرعة إضافة سجلات جديدة كانت محبطة. لذلك ، سنقوم بتعيين من tuples (id1 ، id2) ، حيث id1 ، id2 هي معرفات اللاعبين الذين هم على دراية ببعضهم البعض. في الوقت نفسه ، تخلص من التكرارات.

 df = pd.read_csv('tournaments.csv').set_index('Unnamed: 0') url = 'https://rating.chgk.info/api/tournaments/{}/recaps.json' links = set() for id in df.index: teams = requests.get(url.format(id)).json() for team in teams: t = team["recaps"] for i in range(len(t)): for j in range(i + 1, len(t)): first = int(t[i]["idplayer"]) second = int(t[j]["idplayer"]) if first < second: links.add((first, second)) else: links.add((second, first)) #    sleep(1) clear_output(wait=True) display('Current tournament: ' + str(df.index.get_loc(id) + 1) + '/' + str(len(df))) display('Links total: ' + str(len(links))) 

الحصول على رسم بياني واستكشاف المكونات المتصلة

لذا ، انتهى إعداد البيانات ، فقد حان الوقت لبناء رسم بياني! للقيام بذلك ، سوف نستخدم مكتبة networkx ، التي تعد إمكاناتها كافية لمجموعتنا.

 players = itertools.chain(*links) G = nx.Graph() G.add_nodes_from(players) for t in links: G.add_edge(*t) print(nx.info(G)) 

يوجد الآن حوالي مائتي ألف شخص في مجتمع ChGK ، وفي المتوسط ​​، لعب خبير في المهنة 12 شخصًا:

 Number of nodes: 198145 Number of edges: 1206076 Average degree: 12.1737 

حان الوقت لاكتشاف عدد المكونات المتصلة في الرسم البياني الذي يرجع تاريخه. لدى Networkx وظيفة رائعة تسمى connect_components تقوم بما تحتاج إليه فقط:

 clusters_l = [len(c) for c in sorted(nx.connected_components(G), key=len, reverse=True)] print(clusters_l[:20]) 

يوجد ثلاثة أرباع اللاعبين تقريبًا في مكون واحد متصل ، ويتم تقسيم الباقي إلى أشكال فرعية صغيرة جدًا. هناك أكثر من ثمانية آلاف منهم.

 [145922, 153, 124, 74, 72, 56, 50, 47, 42, 40, 39, 39, 38, 38, 37, 36, 36, 36, 36, 35] 

حتى على نطاق لوغاريتمي ، تبدو هيمنة المكون الرئيسي مثيرة للإعجاب. على المحور X - رقم المكون من الأكبر إلى الأصغر ، على المحور ص - حجمه (المحور لوغاريتمي).

ما سبب هذا التوزيع غير المتكافئ للأشخاص في المكونات المتصلة؟ في رأيي ، النقطة هي هذه:

• تأتي مجموعة صغيرة من الناس إلى اللعبة لأول مرة ، وبالتالي تشكل مجموعة صغيرة تتسع لأربعة إلى ستة أشخاص ؛
• إذا كان لدى المدينة بالفعل مجتمع كبير ، فستندمج مثل هذه المجموعة بسرعة مع المجموعة الرئيسية - يحتاج شخص واحد فقط للعب لفريق من المجموعة الرئيسية ؛
• إذا في مدينة ChGK ظهرت للتو ، فإن الكتلة ستعيش لفترة أطول ، لأنه اللعب لفريق من المجموعة الرئيسية أكثر صعوبة.

تشبه العملية تشكيل قطرات المطر في السحب: قطرة كبيرة تجذب قطرات صغيرة وتنمو بسرعة.

قبل التعامل مع المكون الرئيسي ، دعونا ننظر إلى المكونات في المقام الأول أو التاسع (أعتبر أن المكون الرئيسي هو صفر). نحن نختبر الفرضية القائلة بأن الأشخاص في هذه المكونات هم من نفس المدينة. ليس لدى المتذوق أي ارتباط بالمدينة (وهو أمر منطقي في عالمنا الحديث). ومع ذلك ، يمكنك إلقاء نظرة على المنفذ المحلي للفريق الذي لعب من أجله في المرة الأخيرة

 for i in range(1, 10): _g = list(sorted(nx.connected_components(G), key=len, reverse=True)[i]) s = pd.Series() p_url = 'https://rating.chgk.info/api/players/{}/tournaments.json' t_url = 'https://rating.chgk.info/api/teams/{}.json' for player in _g: data = requests.get(p_url.format(player)).json() for item in data: team_id = data[item]["tournaments"][0]["idteam"] data = requests.get(t_url.format(team_id)).json() town = data[0]["town"] s.at[len(s)] = town print(' #{}'.format(i)) print(s.value_counts()) 

لوحة ملخص:

نعم ، التجمعات الصغيرة كلها تقريبا من مدينة واحدة. يرجى الانتباه إلى مكون من اثنين وسبعين من سكان تامبوف ، الذي يرتبط مع لوكسمبورغ. في المركزين السابع والتاسع توجد مكونات من Gorno-Altaysk ، والتي لسبب ما غير مترابطة. أتصور بسهولة كفاح عشيرتين من طراز ChGK ، مثل Montecca و Capulet ، الذين يقاتلون من أجل السيطرة على المدينة.
أفترض أنه في المستقبل القريب سوف تندمج هذه المكونات مع المكونات الرئيسية ولكن سوف تستمر في القتال .

المكون الرئيسي للاتصال

لذلك ، وصلنا إلى المكون الرئيسي. سنحصل على الرسم البياني المطلوب وننظر في إحصاءاته:

 subgraph_v = list(sorted(nx.connected_components(G), key=len, reverse=True)[0]) subgraph = G.subgraph(subgraph_v) print(nx.info(subgraph)) 

تحول متوسط ​​عدد الاتصالات إلى أكثر من ذلك.

 Number of nodes: 145922 Number of edges: 1070504 Average degree: 14.6723 

وما هو الحد الأقصى لعدد الاتصالات لكل لاعب؟

 for t in sorted(G.degree, key=lambda x: x[1], reverse=True)[:10]: print(' {}   {} '.format(t[0], t[1])) 

  42511   818   15051   798   29800   678   23020   666   16581   662   5328   657   29887   651   15811   645   30352   605   1055   602  

بصراحة ، أنا مصدوم قليلاً من الأرقام. إذا كنت تلعب مع فريق جديد في كل مرة ، فستحتاج إلى 818/5 ≈ 164 لعبة للوصول إلى المركز الأول. لا يصدق.
سنتذكر أول اثنين من الخبراء في هذا التصنيف وسنستخدم مهارات الاتصال الخاصة بهم بشكل أكبر.
دعونا نقدر عدد أقرب معارفه لدى خبير متوسط:

 _count = 50 values = nx.degree_histogram(subgraph) plt.figure(figsize=(16, 8), dpi=80) plt.plot(range(_count),values[:_count],'ro-') # in-degree plt.xlabel(' ', fontsize=18) plt.xticks(range(0,_count, 5)) plt.ylabel(' ', fontsize=18) plt.title(' ', fontsize=22) plt.show() 

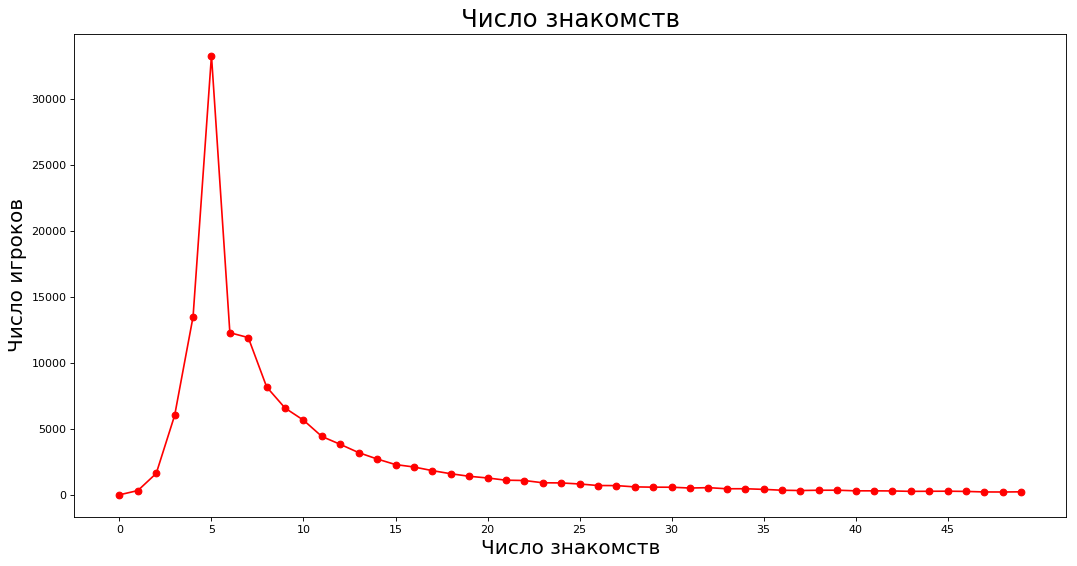
على المحور X - عدد أقرب معارفه ، على المحور Y - عدد الخبراء الذين لديهم العدد المقابل من المعارف. على سبيل المثال ، يوجد لدى حوالي 40،000 خبير خمسة معارف.
لاحظ أن الموضة لها 5 معارف (من المضحك أن ما يصل إلى ستة أشخاص يمكن أن يكونوا على الطاولة). في الوقت نفسه ، يبلغ المتوسط ​​الحسابي لعدد معارفه 14.67 ، والوسيط هو 7. والحقيقة هي أن السادة من التصنيف أعلاه يبالغون في تقدير المتوسط ​​إلى حد كبير. إذا لم يكن هناك مائة شخص يلعبون في ChGK ، ولديهم 800 من معارفه ، فإنهم يلعبون في المتوسط ​​في ChGK.

المسافات للاعبين

لأن من الصعب بعض الشيء حساب قطر مثل هذا الرسم البياني ، فلنفعل ذلك أسهل: خذ قائمة بعدة لاعبين وابحث عن أقصر المسافات من بينها إلى خبراء آخرين. بصفتي هؤلاء اللاعبين ، أخذت العديد من الخبراء المعروفين ، وأنا ، لاعب عشوائي وخبيرين لديهم أكبر عدد من المعارف (انظر التصنيف أعلاه). إليك ما حدث:

 famous_players = {9808: ' ', 5195: ' ', 25882: ' ', 29333: ' ', 118622: ' ', 42511: ' ', 15051: ' ', 118621: ' '} for key in famous_players: print('{}: {} -      ' .format(famous_players[key], nx.eccentricity(subgraph, v=key))) 

  : 12 -        : 12 -        : 12 -        : 12 -        : 13 -        : 12 -        : 13 -        : 13 -       

اتضح أن صياغة قوية لنظرية المصافحة الستة (أي شخصين مفصولين بما لا يزيد عن خمسة مستويات من الأصدقاء المشتركين) غير صحيحة. قطر الرسم البياني على الأرجح 13-14.
ماذا عن صيغة أضعف (أي شخصين في المتوسط يفصل بينهما ما لا يزيد عن خمسة مستويات من الأصدقاء المشتركين)؟

 for key in famous_players: paths = nx.shortest_path_length(subgraph, source=key).values() print('{}: {} -      ' .format(famous_players[key], sum(paths) / len(paths))) 

  : 3.941461876893135 -        : 3.7971107852140182 -        : 3.89353216101753 -        : 3.8634887131481204 -        : 4.1443373857266215 -        : 3.575478680390894 -        : 3.608674497334192 -        : 4.564102739819904 -       

إذا قمنا بفك الصياغة ، فإن النظرية تتحقق - في المتوسط ​​بين الخبراء من 4 إلى 5 مستويات من المعارف. نحن نرسم كم من الناس على دراية بخبير عشوائي Druzem مباشرة ، من خلال واحد أو اثنين ، الخ خبراء.

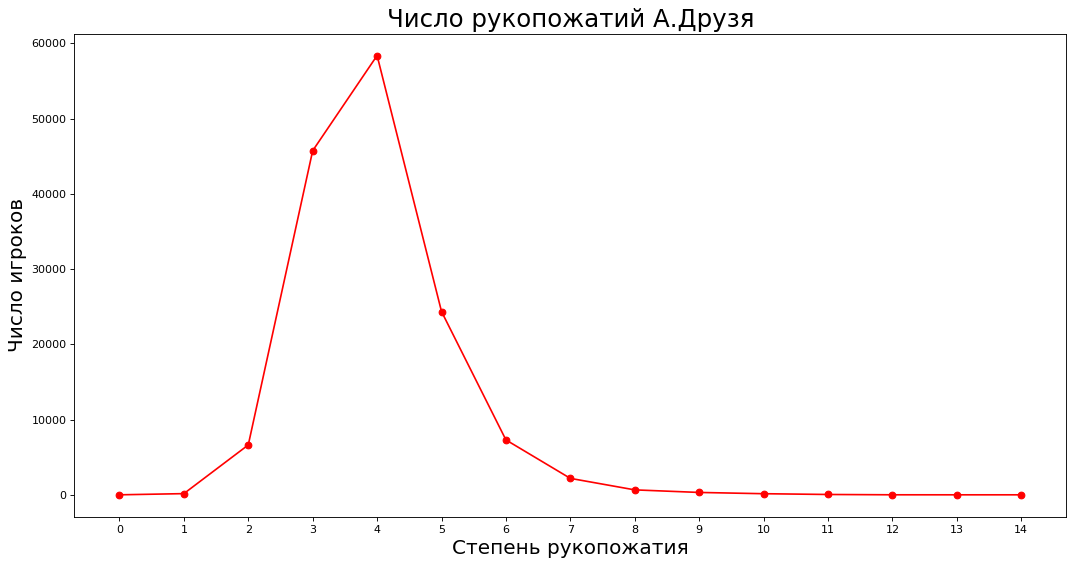
 paths = nx.shortest_path_length(subgraph, source=9808) neighbours = [0] * 15 for k in paths: neighbours[paths[k]] += 1 _count = 15 plt.figure(figsize=(16, 8), dpi=80) plt.plot(range(_count),neighbours[:_count],'ro-') # in-degree plt.xlabel(' ', fontsize=18) plt.xticks(range(_count)) plt.ylabel(' ', fontsize=18) plt.title('  .', fontsize=22) plt.show() 

على المحور X ، درجة التعارف مع A. Druzem (مباشرة ، من خلال واحد ، اثنان ، إلخ) ، على المحور Y ، عدد الخبراء الذين هم على دراية A. Druzem بهذه الطريقة.

الرسوم البيانية الاجتماعية

لأن لا يمثل إنشاء رسم بياني لحوالي 200 ألف شخص فكرة جيدة ، وسنيسر الأمر: سنقوم ببناء مكون اتصال Kerch ورسم بياني للأشخاص المرتبطين بالمؤلف.

مكون كيرتش

 little_v = list(sorted(nx.connected_components(G), key=len, reverse=True)[1]) little = G.subgraph(little_v) plt.figure(figsize=(24, 12), dpi=200) pos = nx.kamada_kawai_layout(little) nx.draw(little, pos=pos, node_size=100, edge_color='gray', node_color=[val for (node, val) in little.degree()], cmap=plt.cm.jet) plt.show() 

تستطيع أن ترى فصل المكونات إلى فرق. علاوة على ذلك ، فإن الفرق مترابطة بمساعدة وكبير من خبراء اجتماعيين أو اثنين. يوجد في الوسط مجموعة صغيرة جدًا من الخبراء الذين لعبوا مع عدد كبير من اللاعبين الآخرين.

عدد شخص واحد

سوف نجد أقرب معارف شخص واحد ونرى كيف ترتبط. لتبسيط الرسم البياني ، لن نضيف الشخص نفسه (هو مرتبط بالفعل مع الجميع)

 id = 118622 ego_graph = [n for n in G.neighbors(id)] #ego_graph.append(id) ego_graph = G.subgraph(ego_graph) plt.figure(figsize=(24, 16), dpi=200) pos = nx.kamada_kawai_layout(ego_graph) nx.draw(ego_graph, pos=pos, node_size=100, edge_color='gray', node_color=[val for (node, val) in ego_graph.degree()], cmap=plt.cm.jet) plt.show() 

الرسم البياني أكثر كثافة ، نواة من 10 إلى 15 شخصًا على دراية ببعضهم البعض يمكن تمييزها. الحد الأقصى لحجم النقرة هو 13.

استنتاج

• من الصعوبة بمكان التعرف على شخص في ChGK رياضي أكثر من شبكة اجتماعية ، فأنت بحاجة إلى عدم الاتصال بالإنترنت ولعب دورة واحدة على الأقل. في الوقت نفسه ، ينتشر الخبراء في جميع أنحاء العالم. ومع ذلك ، فإن متوسط المسافة بين الخبراء هو في الواقع أقل من خمسة.
• يستخدم موقع التصنيف رقم Snyatkovsky ، وهو رقم تناظري لعدد Erdös في عالم ChGK. السيد Snyatkovsky نفسه يحتل المركز الثالث في الترتيب لدينا من خبراء الأكثر مؤنس.
• رمز من مقال في جيثب بلدي.
• للتعليقات القيمة ، فإن المؤلف ممتن لـ White Noise و Who Framed Roger Federer و Mikhail Akulov و Vera Terentyeva و Firemoon .