مرحبا بالجميع! انتهت عطلات رأس السنة ، مما يعني أننا مستعدون مرة أخرى لمشاركة المواد المفيدة معك. تم إعداد ترجمة لهذه المقالة تحسباً لإطلاق دفق جديد في الدورة التدريبية "الخوارزميات للمطورين" .
دعنا نذهب!
ربما تكون طريقة الانتشار الخلفي للخطأ هي العنصر الأساسي في الشبكة العصبية. تم وصفه لأول مرة في الستينيات ، وبعد 30 عامًا تقريبًا ، شاع روملهارت وهينتون وويليامز في مقال بعنوان
"تعلم التمثيل عن طريق أخطاء التكاثر" .
يتم استخدام الطريقة لتدريب شبكة عصبية بشكل فعال باستخدام قاعدة السلسلة المسماة (قاعدة التمييز بين دالة معقدة). ببساطة ، بعد كل تمريرة عبر الشبكة ، يؤدي الانتشار الخلفي إلى تمريرة في الاتجاه المعاكس ويقوم بضبط معلمات النموذج (الأوزان والتشريد).
في هذه المقالة ، أود أن أعتبر بالتفصيل من وجهة نظر رياضية عملية التعلم وتحسين شبكة عصبية بسيطة مكونة من 4 طبقات. أعتقد أن هذا سوف يساعد القارئ على فهم كيفية عمل backpropagation ، وكذلك إدراك أهميته.
تحديد نموذج الشبكة العصبية
تتكون الشبكة العصبية المكونة من أربعة طبقات من أربعة خلايا عصبية في طبقة الإدخال ، وأربعة خلايا عصبية في الطبقات المخفية و 1 خلية عصبية في طبقة المخرجات.
صورة بسيطة لشبكة عصبية من أربع طبقات.طبقة الإدخال
في الشكل ، تمثل الخلايا العصبية الأرجواني المدخلات. يمكن أن تكون كميات عددية بسيطة أو أكثر تعقيدًا - ناقلات أو مصفوفات متعددة الأبعاد.
المعادلة التي تصف المدخلاتالمجموعة الأولى من التنشيط (أ) تساوي قيم الإدخال. "التنشيط" هو قيمة الخلايا العصبية بعد تطبيق وظيفة التنشيط. انظر أدناه لمزيد من التفاصيل.
طبقات خفية
يتم حساب القيم النهائية في الخلايا العصبية المخفية (في الشكل الأخضر) باستخدام مدخلات مرجحة z في الطبقة
الأولى وتنشيطات
I في الطبقة L. للمعادلات 2 و 3 ، ستكون المعادلات كما يلي:
ل = 2:
ل = 3:
W
2 و W
3 هما الأوزان على الطبقتين 2 و 3 ، و b
2 و b
3 هما الإزاحة على هذه الطبقات.
يتم حساب التفعيلين
2 و
3 باستخدام وظيفة التنشيط f. على سبيل المثال ، هذه الوظيفة f غير خطية (مثل
السيني ،
ReLU و
الظل الزائد ) وتسمح للشبكة بدراسة الأنماط المعقدة في البيانات. لن نتحدث عن كيفية عمل وظائف التنشيط ، ولكن إذا كنت مهتمًا ، أوصي بشدة بقراءة هذا
المقال الرائع.
إذا نظرت عن كثب ، فسترى أن كل x ، z
2 ، a
2 ، z
3 ، a
3 ، W
1 ، W
2 ، b
1 و b
2 لا تحتوي على المؤشرات السفلية الموضحة في الشكل الخاص بالشبكة العصبية ذات الأربع طبقات. الحقيقة هي أننا قمنا بدمج جميع قيم المعلمات في مصفوفات مجمعة حسب الطبقات. هذه طريقة قياسية للعمل مع الشبكات العصبية ، وهي مريحة للغاية. ومع ذلك ، سأذهب من خلال المعادلات بحيث لا يوجد التباس.
لنأخذ الطبقة 2 ومعلماتها كمثال. يمكن تطبيق نفس العمليات على أي طبقة من الشبكة العصبية.
W
1 هو مصفوفة أوزان الأبعاد
(n ، m) ، حيث
n هو عدد الخلايا العصبية الناتجة (الخلايا العصبية في الطبقة التالية) ، و
m هو عدد الخلايا العصبية المدخلة (الخلايا العصبية في الطبقة السابقة). في حالتنا ،
ن = 2 و
م = 4 .
هنا ، يتوافق الرقم الأول في حرف أي من الأوزان مع مؤشر الخلايا العصبية في الطبقة التالية (في حالتنا ، هذه هي الطبقة المخفية الثانية) ، والرقم الثاني يناظر مؤشر الخلايا العصبية في الطبقة السابقة (في حالتنا ، هذه هي طبقة الإدخال).
x هي متجه إدخال البعد (
m ، 1) ، حيث
m هو عدد الخلايا العصبية المدخلة. في حالتنا ،
م = 4.
b
1 هي متجه الإزاحة للبعد (
n ، 1) ، حيث
n هو عدد الخلايا العصبية في الطبقة الحالية. في حالتنا ،
ن = 2.
باتباع المعادلة z
2 ، يمكننا استخدام التعاريف المذكورة أعلاه من W
1 و x و b
1 للحصول على المعادلة z
2 :
الآن انظر بعناية إلى الشكل التوضيحي للشبكة العصبية أعلاه:
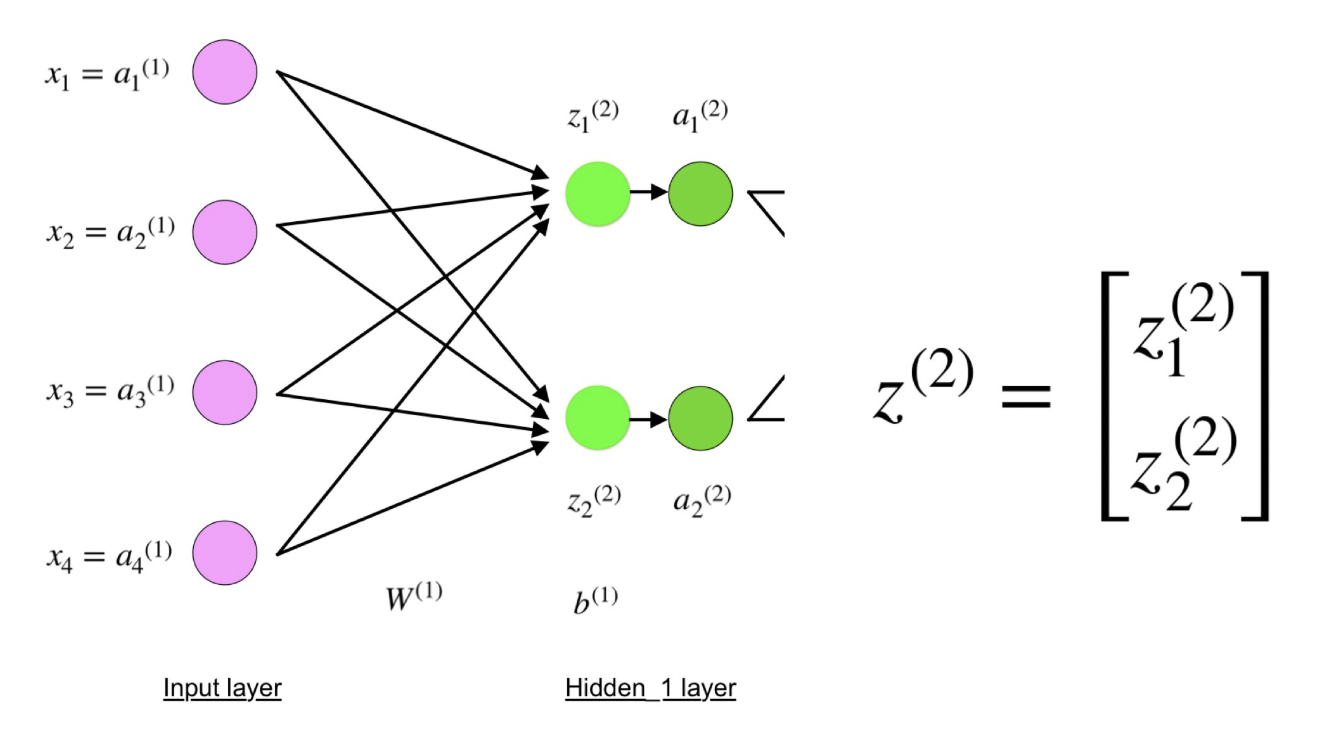
كما ترون ، يمكن التعبير عن z
2 من حيث z
1 2 و z
2 2 ، حيث z
1 2 و z
2 2 هي مجاميع منتجات كل قيمة إدخال x
i بالوزن المقابل W
ij 1 .
هذا يؤدي إلى نفس المعادلة لـ z
2 ويثبت أن تمثيل المصفوفة z
2 و a
2 و z
3 و
3 صحيح.
طبقة الإخراج
الجزء الأخير من الشبكة العصبية هو طبقة المخرجات ، والتي تعطي القيمة المتوقعة. في مثالنا البسيط ، يتم تقديمه في شكل خلية عصبية واحدة ملطخة باللون الأزرق ويتم حسابها على النحو التالي:
مرة أخرى ، نستخدم تمثيل المصفوفة لتبسيط المعادلة. يمكنك استخدام الأساليب المذكورة أعلاه لفهم المنطق الأساسي.
التوزيع المباشر والتقييم
المعادلات المذكورة أعلاه تشكل توزيع مباشر من خلال الشبكة العصبية. هنا لمحة سريعة:
(1) - طبقة الإدخال
(2) - قيمة الخلايا العصبية في الطبقة الأولى المخفية
(3) - قيمة التنشيط على الطبقة الأولى المخفية
(4) - قيمة الخلايا العصبية في الطبقة الثانية المخفية
(5) - قيمة التنشيط في المستوى الثاني المخفي
(6) - طبقة الإخراجالخطوة الأخيرة في المسار المباشر هي تقييم قيمة المخرجات المتوقعة بالنسبة إلى قيمة المخرجات المتوقعة
y .
الإخراج y جزء من مجموعة بيانات التدريب (x ، y) ، حيث
x هي المدخلات (كما نتذكر من القسم السابق).
يحدث التقدير بين
s و
y من خلال دالة الخسارة. يمكن أن يكون بسيطًا
كخطأ قياسي أو أكثر تعقيدًا مثل
إنتروبيا .
نحن نسمي وظيفة الخسارة C هذه ونشير إليها كما يلي:
حيث يمكن أن تتساوى
التكلفة مع الخطأ القياسي ، أو الانتروبيا ، أو أي وظيفة خسارة أخرى.
استنادًا إلى قيمة C ، "يعرف" النموذج كم تحتاج المعلمات إلى تعديل من أجل الاقتراب من قيمة الإخراج المتوقعة من
y . يحدث هذا باستخدام طريقة backpropagation.
عودة انتشار الخطأ وحساب التدرجات
استنادًا إلى مقالة 1989 ، فإن طريقة backpropagation:
يضبط باستمرار أوزان الاتصالات في الشبكة لتقليل قياس الفرق بين متجه الإخراج الفعلي للشبكة ومتجه الإخراج المطلوب .
و
... يجعل من الممكن إنشاء وظائف جديدة مفيدة تميز backpropagation عن الأساليب السابقة والأبسط ...بمعنى آخر ، يهدف backpropagation إلى تقليل وظيفة الخسارة عن طريق ضبط الأوزان والإزاحات للشبكة. يتم تحديد درجة التعديل بواسطة تدرجات دالة الخسارة فيما يتعلق بهذه المعلمات.
يطرح سؤال واحد:
لماذا حساب التدرجات ؟
للإجابة على هذا السؤال ، نحتاج أولاً إلى مراجعة بعض مفاهيم الحوسبة:
تدرج الدالة C (x
1 ، x
2 ، ... ، x
m ) في x هو
ناقل المشتقات الجزئية لـ C
فيما يتعلق x .
يعكس مشتق الدالة C الحساسية للتغير في قيمة الوظيفة (قيمة المخرجات) بالنسبة للتغيير في الوسيطة
x (
قيمة الإدخال ). بمعنى آخر ، يخبرنا المشتق بالاتجاه C. الذي يتحرك.
يوضح التدرج اللوني مدى ضرورة تغيير المعلمة
x (في الاتجاه الموجب أو السلبي) لتقليل C.
يتم حساب هذه التدرجات باستخدام طريقة تسمى
قاعدة السلسلة.
لوزن واحد (w
jk )
l ، يكون التدرج اللوني:
(1) حكم السلسلة
(2) بحكم التعريف ، m هو عدد الخلايا العصبية لكل طبقة l - 1
(3) حساب مشتق
(4) القيمة النهائية
يمكن تطبيق مجموعة مماثلة من المعادلات على (b j ) l :
(1) حكم السلسلة
(2) حساب مشتق
(3) القيمة النهائيةغالبًا ما يطلق على الجزء المشترك في المعادلتين "التدرج المحلي" ويتم التعبير عنه على النحو التالي:
يمكن تحديد "التدرج المحلي" بسهولة باستخدام قاعدة سلسلة. لن أرسم هذه العملية الآن.
التدرجات تسمح بتحسين معلمات النموذج:
حتى يتم الوصول إلى معيار التوقف ، يتم تنفيذ ما يلي:
خوارزمية لتحسين الأوزان والإزاحة (وتسمى أيضًا النسب التدرج اللوني)
- يتم تحديد القيم الأولية لـ w و b بشكل عشوائي.
- إبسيلون (ه) هي سرعة التعلم. وهو يحدد تأثير التدرج.
- w و b هي تمثيل مصفوفة للأوزان والإزاحة.
- يمكن حساب مشتق C فيما يتعلق بـ w أو b باستخدام مشتقات جزئية من C فيما يتعلق بالأوزان الفردية أو الإزاحة.
- يتم استيفاء شرط الإنهاء بمجرد تقليل وظيفة الخسارة.
أريد أن أخصص الجزء الأخير من هذا القسم لمثال بسيط نحسب فيه التدرج C بالنسبة لوزن واحد (وزن
22 )
2 .
دعنا نضيف إلى أسفل الشبكة العصبية المذكورة أعلاه:
التمثيل المرئي لل backpropagation في الشبكة العصبيةيربط الوزن (وزن
22 )
2 (a
2 )
2 و (z
2 )
2 ، لذا فإن حساب التدرج يتطلب تطبيق قاعدة السلسلة على (z
2 )
3 و (a
2 )
3 :
يتطلب حساب القيمة النهائية لمشتق C من (a
2 )
3 معرفة الوظيفة C. بما أن C تعتمد على (a
2 )
3 ، يجب أن يكون حساب المشتق بسيطًا.
آمل أن يكون هذا المثال قد تمكن من إلقاء بعض الضوء على الرياضيات وراء حساب التدرجات. إذا كنت ترغب في معرفة المزيد ، فإنني أوصي بشدة بمراجعة سلسلة من المقالات في Stanford NLP ، حيث يقدم ريتشارد Socher 4 تفسيرات رائعة للطلاء الخلفي.
ملاحظة ختامية
في هذه المقالة ، شرحت بالتفصيل كيف يعمل التكرار الخلفي لخطأ ما تحت غطاء محرك السيارة باستخدام الأساليب الرياضية مثل حساب التدرجات ، سلسلة القاعدة ، إلخ. إن معرفة آليات هذه الخوارزمية ستقوي معرفتك بالشبكات العصبية وتتيح لك الشعور بالراحة عند العمل مع نماذج أكثر تعقيدًا. حظا سعيدا في رحلة التعلم العميق الخاص بك!
هذا كل شيء. ندعو الجميع إلى ندوة مجانية على الإنترنت حول موضوع "شجرة الشرائح: بسيطة وسريعة" .