🍾 👄 🗣️ الفرز الهجين ♐️ ♓️ 🧝🏾

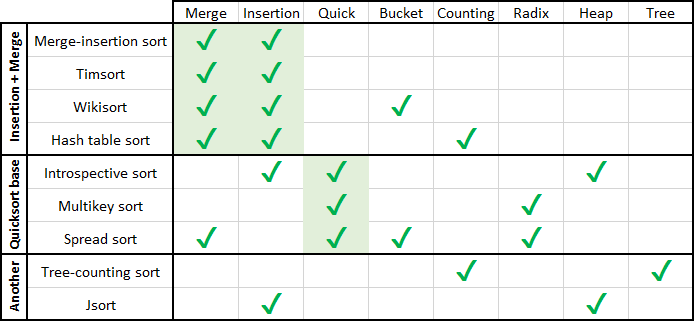
كما يعلم الجميع بالفعل ، يمكن أن يعتمد الفرز على عمليات التبادل والإدراج والاختيار والاندماج والتوزيع.

ولكن إذا تم دمج طرق مختلفة في الخوارزمية ، فإنها تنتمي إلى فئة الأنواع المختلطة.

كُتب هذا المقال بدعم من إديسون.

نحن منخرطون في استكمال وصيانة المواقع على 1C-Bitrix ، وكذلك تطوير تطبيقات الأجهزة المحمولة Android و iOS .

نحن نحب نظرية الخوارزميات! ؛-)

دعنا نتذكر بسرعة خوارزميات فرز الفئات وما هي ميزات كل منها.

أنواع التبادل

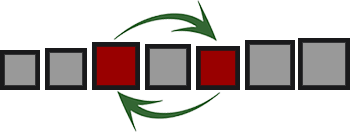
تتم مقارنة عناصر الصفيف في أزواج مع بعضها البعض ويتم إجراء تبادل للأزواج المختلين.

الممثل الأكثر فعالية لهذه الفئة هو النوع الأسطوري السريع .

أنواع الإدراج

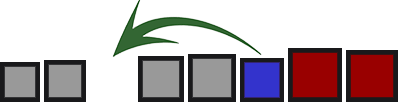
يتم إدراج عناصر من الجزء غير المصنف من المصفوفة في أماكنها في المنطقة التي تم فرزها.

من هذه الفئة ، غالبًا ما يتم استخدام الفرز بواسطة إدخالات بسيطة . على الرغم من أن هذه الخوارزمية لها متوسط تعقيد O ( n ² ) ، فإن هذا الفرز يعمل بسرعة كبيرة مع المصفوفات المطلوبة تقريبًا - ويصل التعقيد عليها إلى O ( n ). بالإضافة إلى ذلك ، يعد هذا الفرز أحد أفضل الخيارات لمعالجة المصفوفات الصغيرة.

الفرز باستخدام شجرة البحث الثنائية ينتمي أيضًا إلى هذه الفئة.

الترتيب حسب الاختيار

في المنطقة غير المرتبة ، يتم تحديد الحد الأدنى / الحد الأقصى للعنصر ، والذي يتم نقله إلى نهاية / بداية الجزء غير المصنف من الصفيف.

الفرز باستخدام اختيار بسيط يعمل ببطء شديد (في المتوسط O ( n ² )) ، ولكن في هذه الفئة ، يوجد ترتيب صعب بواسطة كومة (يُعرف أيضًا بالفرز الهرمي ) ، والذي له تعقيد زمني لـ O ( n log n ) - وهو أمر ذو قيمة كبيرة ، لا توجد حالات تدهور في هذا الفرز ، أيا كانت البيانات الواردة. بالمناسبة ، لا يحتوي هذا الفرز على أفضل الحالات للبيانات الواردة أيضًا.

دمج الأنواع

تؤخذ المساحات المصنفة في الصفيف ويتم دمجها ، أي يتم دمج الصفائف الفرعية المصغرة المصغرة في صفيف فرعي أكبر.

إذا تم تصنيف مصفحتين فرعيتين ، فإن الجمع بينهما سيكون عملية سهلة التنفيذ وسريعة التوقيت. الجانب الآخر للعملة هو أن الدمج يتطلب تقريبًا تكلفة الذاكرة الإضافية O ( n ) - على الرغم من أن هناك القليل جدًا من الخيارات المعقدة للغاية للفرز مع الدمج ، حيث تكون تكلفة الذاكرة هي O (1).

الترتيب حسب التوزيع

يتم توزيع عناصر الصفيف وإعادة توزيعها في الفئات حتى يقبل الصفيف حالة مصنفة.

تنتشر العناصر في مجموعات إما وفقًا لقيمتها (ما يسمى بفرز العد ) أو استنادًا إلى قيمة الأرقام الفردية (هذه هي بالفعل فرزات ثنائية الاتجاه ).

الفرز دلو ينتمي أيضا إلى هذه الفئة.

تتمثل ميزة الفرز حسب التوزيع في أنها إما لا تستخدم مقارنات زوجية للعناصر فيما بينها ، أو أن مثل هذه المقارنات موجودة إلى حد ما. لذلك ، يكون الفرز حسب التوزيع غالبًا متقدمًا للسرعة ، على سبيل المثال ، الفرز السريع. من ناحية أخرى ، غالبًا ما يتطلب الفرز حسب التوزيع الكثير من الذاكرة الإضافية ، نظرًا لأن مجموعات العناصر التي يتم إعادة توزيعها باستمرار تحتاج إلى تخزينها في مكان ما.

إن النزاعات حول أي الفرز هي الأفضل بشكل متكرر للغاية ، ولكن حقيقة الأمر هي أنه لا توجد خوارزمية مثالية ولا يمكن أن تكون مناسبة لجميع المناسبات. على سبيل المثال ، يكون الفرز السريع سريعًا جدًا (ولكن ليس الأسرع) في معظم المواقف ، ولكنه يأتي أيضًا في حالات تدهور يحدث فيها تعطل. يكون الفرز بواسطة إدخالات بسيطة بطيئًا ، ولكن بالنسبة للصفائف التي يتم طلبها تقريبًا ، سيتجاوز بسهولة الخوارزميات الأخرى. يعمل فرز كومة الذاكرة المؤقتة بسرعة كبيرة مع أي بيانات واردة ، ولكن ليس بالسرعة التي تتم بها عمليات الفرز الأخرى في ظل ظروف معينة ولا توجد طريقة لتسريع الهرم. يكون دمج الفرز أبطأ من الفرز السريع ، ولكن إذا كانت هناك صفائف فرعية مصنفة في الصفيف ، فمن الأسرع دمجها بدلاً من الفرز بواسطة الفرز السريع. إذا كان للصفيف العديد من العناصر المكررة أو رتبنا الصفوف ، فمن الأرجح أن الفرز حسب التوزيع هو الخيار الأفضل. كل طريقة جيدة بشكل خاص في موقفها الأكثر ملاءمة.

ومع ذلك ، يستمر المبرمجون في ابتكار أسرع الفرز في العالم ، حيث يقومون بتجميع الطرق الأكثر فاعلية من مختلف الطبقات. دعونا نرى مدى نجاحها بالنسبة لهم.

نظرًا لأن العديد من الخوارزميات غير التافهة مذكورة في المقالة ، فإنني أغطي فقط بإيجاز المبادئ الأساسية لأعمالهم ، دون أن أفرط في تحميل المقالة بالرسوم المتحركة والتفسيرات التفصيلية. في المستقبل سيكون هناك مقالات منفصلة ، حيث سيكون هناك كاريكاتير لكل خوارزمية والفروق الدقيقة التفصيلية.

إدراج + دمج

الاستنتاج التجريبي المحض هو أن الانصهار و / أو الإدراج يستخدم في الغالب في الهجينة. في معظم الفرز ، يتم العثور على طريقة أو أخرى ، أو كليهما معًا. وهناك تفسير منطقي لهذا.

يسعى مخترعو الفرز غالبًا إلى إنشاء خوارزميات متوازية تطلب في وقت واحد أجزاء مختلفة من صفيف. أفضل طريقة للتعامل مع العديد من المصفوفات الفرعية المصنفة هي دمجها - سيكون هذا هو الأسرع.

الخوارزميات الحديثة غالبا ما تستخدم العودية. أثناء الهبوط المتكرر ، يتم تقسيم الصفيف عادة إلى جزأين ؛ في أدنى مستوى ، يتم طلب الصفيف. عند العودة إلى مستويات أعلى من العودية ، فإن السؤال الذي يطرح نفسه هو الجمع بين الطبقات الفرعية المصنفة في مستويات أقل.

بالنسبة للإدراج ، في الخوارزميات المختلطة في مراحل معينة ، غالبًا ما يتم الحصول على ما يقرب من المصفوفات الفرعية المطلوبة ، والتي من الأفضل أن تؤدي إلى الترتيب النهائي بمساعدة الإضافات.

تحتوي هذه المجموعة على أنواع مختلطة ، حيث يوجد دمج وإدخال ، وتستخدم هذه الطرق بشكل مختلف جدًا.

دمج نوع الإدراج
خوارزمية فورد جونسون :: خوارزمية فورد جونسون

دمج + إدراج

طريقة قديمة للغاية ، بالفعل في عام 1959. تم وصفه بالتفصيل في العمل الخالد لـ Donald Knuth ، "فن البرمجة" ، المجلد 3 ، "الفرز والبحث" ، الفصل 5 ، "الفرز" ، القسم 5.3 ، "الفرز الأمثل" ، القسم الفرعي ، "الفرز مع أقل عدد ممكن من المقارنات" ، وجزء "الفرز حسب الإدخالات والدمج". .

الفرز الآن ليس له قيمة عملية ، لكنه مثير للاهتمام لأولئك الذين يحبون نظرية الخوارزميات. تعتبر مشكلة إيجاد طريقة لفرز العناصر n بأقل عدد من المقارنات. يُقترح تعديل استدلالي غير تافه لفرز الإدراج (مثل هذا الإدراج الذي لن تجده في أي مكان آخر) باستخدام أرقام Jacobstal من أجل تقليل عدد المقارنات. حتى الآن ، من المعروف أيضًا أن هذا ليس هو الخيار الأفضل ، ويمكنك حتى التفادي بمهارة أكبر والحصول على عدد أقل من المقارنات. بشكل عام ، لا يكون الفرز الأكاديمي القياسي ذو فائدة عملية ، لكن بالنسبة للخبراء من هذا النوع ، من دواعي سروري تفكيك مثل هذه الحيل بانحياز جبري.

تيم فرز :: Timsort

إدراج + دمج

كتب بواسطة تيم بيترز منذ 15 سنة والآن

هذا الفرز على حبري يتذكر كثيرًا.
الأطروحة: في صفيف ، يتم البحث عن المصفوفات الفرعية الصغيرة المطلوبة تقريبًا والتي يتم استخدام فرز الإدراج. ثم يتم دمج هذه الصفائف الفرعية باستخدام الدمج.

الدمج في TimSort هو الجزء الأكثر إثارة للاهتمام: تم دمج الدمج التصاعدي الكلاسيكي في المواقف المختلفة. على سبيل المثال ، من المعروف أن الدمج أكثر فاعلية إذا كانت المصفوفات الفرعية المرتبطة متساوية في الحجم تقريبًا. في TimSort ، إذا كانت الأحجام مختلفة تمامًا ، فبعد إجراء إضافي ، يكون هناك ضبط (يمكننا القول أنه من خلال الطبقة الفرعية الأكبر "بعض" العناصر سوف "تتدفق" إلى عنصر أصغر ، وبعد ذلك سوف يستمر الدمج في الوضع القياسي). يتم أيضًا توفير العديد من المواقف الخبيثة - على سبيل المثال ، إذا كانت جميع العناصر في أحد الطبقات الفرعية ستكون أقل من الأخرى. في هذه الحالة ، ستكون المقارنة بين العناصر من كلا الصفيفين خاملاً. إن إجراء الاندماج المعدل "يلاحظ" مثل هذا التطور غير المرغوب فيه للأحداث في الوقت المحدد ، وإذا كان "مقتنعًا" بخيار متشائم باستخدام البحث الثنائي ، فسوف يتحول إلى خيار معالجة أفضل.

في المتوسط ، يعمل هذا الفرز بشكل أبطأ قليلاً من QuickSort ، ومع ذلك ، إذا كان الصفيف الوارد يحتوي على عدد كاف من تكرارات العناصر المطلوبة ، فإن السرعة تزداد بشكل ملحوظ وهنا TimSort تتقدم الباقي.

كتلة دمج الفرز :: كتلة دمج الفرز
ويكي فرز :: ويكي فرز
فرز الكأس المقدسة :: Grailsort

إدراج + دمج + دلاء

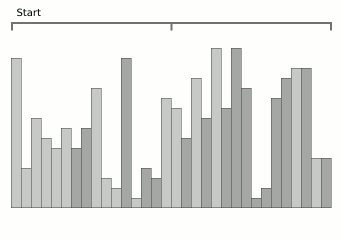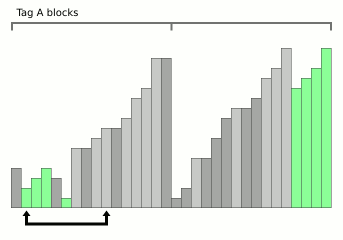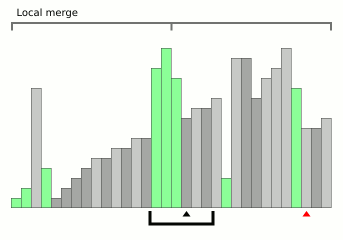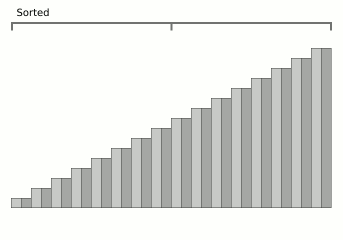دمج دمج فرز الرسوم المتحركة من ويكيبيديا.

هذا هو جديد جدا (2008) وفي الوقت نفسه خوارزمية واعدة للغاية. الحقيقة هي أن مشكلة الدمج المهمة نسبياً هي تكلفة الذاكرة الإضافية. عادة ، حيث يوجد دمج ، هناك أيضًا تعقيد الذاكرة O ( n ).

ولكن تم تصميم WikiSort بحيث يحدث الدمج دون استخدام ذاكرة إضافية - وهذا يعد نادرًا للغاية بين أنواع الدمج. بالإضافة إلى ذلك ، الخوارزمية مستقرة. حسنًا ، إذا كان لفرز الدمج التقليدي أفضل سرعة حسابية O ( n log n ) ، فإن هذا المؤشر في wiki يكون O ( n ). حتى وقت قريب ، كان يعتقد أن دمج الفرز مع هذه المجموعة من الخصائص كان مستحيلاً من حيث المبدأ ، لكن المبرمجين الصينيين فاجأوا الجميع.

الخوارزمية معقدة للغاية لشرحها في جملتين. لكن في يوم من الأيام ، سأكتب مسيرة منفصلة عنه.

في البداية ، تم تسمية الخوارزمية بدون اسم Block Block Merge Sort ، بيد اليد الخفيفة لـ Tim Peters ، الذي درس الفرز بالتفصيل (لتحديد ما إذا كان ينبغي نقل بعض أفكاره إلى TimSort) ، اسم WikiSort تمسك به.

يعمل هابرويزر الذي يغادر في وقت غير محدد Mrrl بشكل مستقل لعدة سنوات على دمج الفرز ، والتي ستكون سريعة في وقت واحد مع أي بيانات واردة ، واقتصادية في الذاكرة ، ومستقرة. لقد نجحت عمليات البحث الإبداعية التي قام بها فيما بعد ووصف الخوارزمية المطورة بأنها فرز للكأس المقدسة (لأنها تلبي جميع متطلبات "الفرز المثالي"). تتشابه معظم أفكار هذه الخوارزمية مع تلك المطبقة في WikiSort ، على الرغم من أن هذه الأنواع ليست متطابقة ويتم تطويرها بشكل مستقل عن بعضها البعض.

فرز جدول التجزئة :: فرز جدول التجزئة

توزيع + إدراج + دمج

يتم تقسيم الصفيف بشكل متكرر إلى النصف ، حتى يصل عدد العناصر في المصفوفات الفرعية الناتجة إلى قيمة عتبة معينة. عند أدنى مستوى من العودية ، يحدث توزيع تقريبي (باستخدام جدول تجزئة) ويتم فرز المصفوفة الفرعية بواسطة إدراجات. ثم هناك عودة متكررة إلى مستويات أعلى ، ويتم الجمع بين نصفي فرزها عن طريق الدمج.

تحدثت أكثر قليلاً عن هذه الخوارزمية قبل شهر .

فرز سريع كما الابتدائية

بعد الدمج والإدراج ، يحتل المركز الثالث في عرض الهجين المختلط بحزم الترتيب السريع المفضل لدى الجميع.

هذه خوارزمية فعالة للغاية ، ولكن هناك حالات متدهورة لها أيضًا. يحاول بعض المخترعين جعل QuickSort معرضين تمامًا لأي بيانات واردة سيئة ويقترحون استكمالها بأفكار قوية من أنواع أخرى.

نوع الاستبطان :: Introsort ، الفرز الاستقرائي ، الأمراض المنقولة جنسيا :: الفرز

سريع + كومة + إدراج

فرز الكومة أبطأ إلى حد ما من الفرز السريع ، ولكن في نفس الوقت ، على عكس QuickSort ، فإنه لا يحتوي على حالات متدهورة - متوسط ، أفضل وأسوأ تعقيد وقت حسابي هو O ( n log n ).

لذلك ، اقترح David Musser أن يكون آمنًا أثناء الفرز السريع - إذا كان هناك الكثير من التعشيش ، فيُعتبر هذا بمثابة هجوم على النظام ، والذي تراجع عن مجموعة "سيئة". يحدث التبديل إلى الفرز بواسطة كومة الذاكرة المؤقتة ، وهو ليس ميغابايت ، ولكن ليس بطيئًا في التعامل مع أي بيانات واردة.

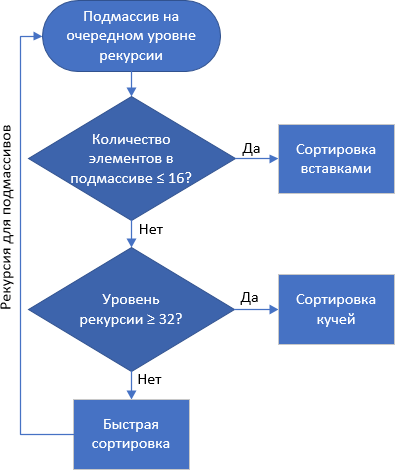
يحتوي C ++ على خوارزمية تدعى std :: sort ، وهو تطبيق للفرز الاستقرائي. إضافة صغيرة - إذا كان في المستوى التالي من العودية ، فإن عدد عناصر المصفوفة الفرعية هو ≤ 16 ، ثم يتم تطبيق فرز الإدراج على المصفوفة الفرعية.

ترتيب multikey :: ترتيب multikey
ترتيب سريع Bitwise :: ترتيب سريع الجذر

سريع + الرتب

فرز سريع ، تتم مقارنة قيم عناصر المصفوفة فقط مع بعضها البعض ، ولكن أرقامها الفردية (أولاً ، نقوم بترتيب الأرقام العليا بهذه الطريقة ، ننتقل من الأصغر منها إلى).

أو هكذا - يتم إجراء الفرز بترتيب البت بترتيب عالٍ ، ويتم الترتيب داخل البتة التالية وفقًا لخوارزمية الفرز السريع.

مبعثر فرز :: Spreadsort

سريع + دمج + دلاء + تصريفات

Gestalt من فرز سريع ، دمج الفرز ، فرز الجرد ، والفرز bitwise.

باختصار لا تفسر. سنقوم بتحليل هذه الخوارزمية بالتفصيل في واحدة من المقالات التالية.

الهجينة الأخرى

فرز العد شجرة

عد + شجرة

الخوارزمية المقترحة من قبل المستخدم AlexanderUsatov . فرز الفرز ، يتم تخزين عدد المفاتيح التي تم حسابها في شجرة متوازنة.

J- نوع :: J- نوع

كومة + إدراج

لقد كتبت بالفعل عن هذا الفرز منذ 5 سنوات . كل شيء بسيط للغاية - أولاً في المصفوفة تحتاج إلى إنشاء كومة غير متزايدة مرة واحدة ، ثم فعل العكس تمامًا - قم ببناء مرة واحدة غير متناقصة. كنتيجة للعملية الأولى ، سيكون الحد الأدنى في المقام الأول للصفيف ، وسوف تنتقل العناصر الصغيرة ككل بشكل كبير إلى البداية. في الحالة الثانية ، سيكون الحد الأقصى في المكان الأخير ، ويتم ترحيل العناصر الكبيرة في نهاية الصفيف. بشكل عام ، نحصل على مجموعة مرتبة تقريبًا ونعمل بها ماذا؟ هذا صحيح - فرز إدراج.