 ترجمة longread مثيرة للاهتمام المكرسة لتصور المفاهيم من نظرية المعلومات. في الجزء الأول ، سننظر في كيفية تمثيل توزيعات الاحتمال بيانياً وتفاعلها والاحتمالات الشرطية. بعد ذلك ، سنتعامل مع الرموز ذات الطول الثابت والمتغير ، ونرى كيف تم بناء الكود الأمثل ولماذا. كملحق ، المفهوم الإحصائي لسيمبسون مفهومة بصريًا.
ترجمة longread مثيرة للاهتمام المكرسة لتصور المفاهيم من نظرية المعلومات. في الجزء الأول ، سننظر في كيفية تمثيل توزيعات الاحتمال بيانياً وتفاعلها والاحتمالات الشرطية. بعد ذلك ، سنتعامل مع الرموز ذات الطول الثابت والمتغير ، ونرى كيف تم بناء الكود الأمثل ولماذا. كملحق ، المفهوم الإحصائي لسيمبسون مفهومة بصريًا.تعطينا نظرية المعلومات لغة دقيقة لوصف أشياء كثيرة. ما مقدار عدم اليقين الموجود بي؟ ما مدى معرفة إجابة السؤال A بإخباري عن إجابة السؤال B؟ ما مدى تشابه مجموعة من المعتقدات مع مجموعة أخرى؟ كان لدي نسخ غير رسمية من هذه الأفكار عندما كنت طفلاً صغيراً ، لكن نظرية المعلومات تتبلور في أفكار دقيقة وقوية. تحتوي هذه الأفكار على مجموعة كبيرة من التطبيقات ، من ضغط البيانات إلى فيزياء الكم والتعلم الآلي والمساحات الشاسعة بينها.
لسوء الحظ ، يمكن أن تبدو نظرية المعلومات مخيفة. لا أعتقد أن هناك أي سبب لذلك. في الواقع ، يمكن شرح العديد من الأفكار الرئيسية بصريا!
احتمال توزيع التصور
قبل الخوض في نظرية المعلومات ، دعونا نفكر في كيفية تصور توزيعات الاحتمالات البسيطة. سنحتاج إليها لاحقًا ، بالإضافة إلى أن هذه التقنيات لتصور الاحتمالات مفيدة في حد ذاتها!
انا في كاليفورنيا في بعض الأحيان تمطر ، ولكن في الغالب الشمس! قل ، 75٪ من الوقت مشمس. من السهل تصوير الصورة:
في معظم الأيام أرتدي قميصًا ، لكني أحيانًا أرتدي معطف واق من المطر. لنفترض أنني أرتدي معطف واق من المطر 38٪ من الوقت. هذا هو أيضا من السهل تصوير.
ماذا لو كنت أرغب في تصور كلتا الحقائق في نفس الوقت؟ الأمر بسيط إذا لم يتفاعلوا - أي مستقلة. على سبيل المثال ، إذا كان ذلك: أن أرتدي قميصًا أو معطف واق من المطر اليوم لا يعتمد على الطقس الأسبوع المقبل. يمكننا تصوير ذلك باستخدام محور واحد لمتغير واحد والآخر للآخر:

إيلاء الاهتمام لخطوط عمودية وأفقية مستقيمة تعمل من خلال. هذا هو ما يشبه الاستقلال! احتمال أن أرتدي معطف واقٍ من المطر لن يتغير نظرًا لحقيقة أنه سيتمطر خلال أسبوع. وبعبارة أخرى ، فإن احتمال أن أرتدي معطف واق من المطر وأن تمطر في الأسبوع المقبل يساوي احتمال أن أرتدي معطف واق من المطر مرات احتمال أن تمطر. انهم لا يتفاعلون.
عندما تتفاعل المتغيرات ، قد يزداد الاحتمال لبعض أزواج المتغيرات ويقلل بعضها البعض. هناك احتمال كبير أن أرتدي معطف واق من المطر ، وتمطر لأن المتغيرات مترابطة ، تجعل بعضها البعض أكثر احتمالا. من المحتمل أن أرتدي معطف واق من المطر في يوم تمطر فيه الأمطار أكثر من احتمال أن أرتدي معطف واق من المطر في يوم ما وأن تمطر في يوم عشوائي آخر.
بصريا ، يبدو أن بعض المربعات تضخم باحتمال إضافي ، في حين أن المربعات الأخرى ضيقة ، لأنه من غير المحتمل أن يحدث حدثان في وقت واحد:
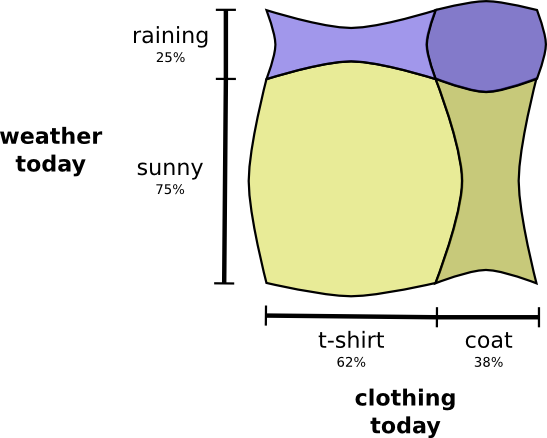
ولكن على الرغم من أنها تبدو باردة ، إلا أنها ليست مفيدة للغاية لفهم ما يحدث.
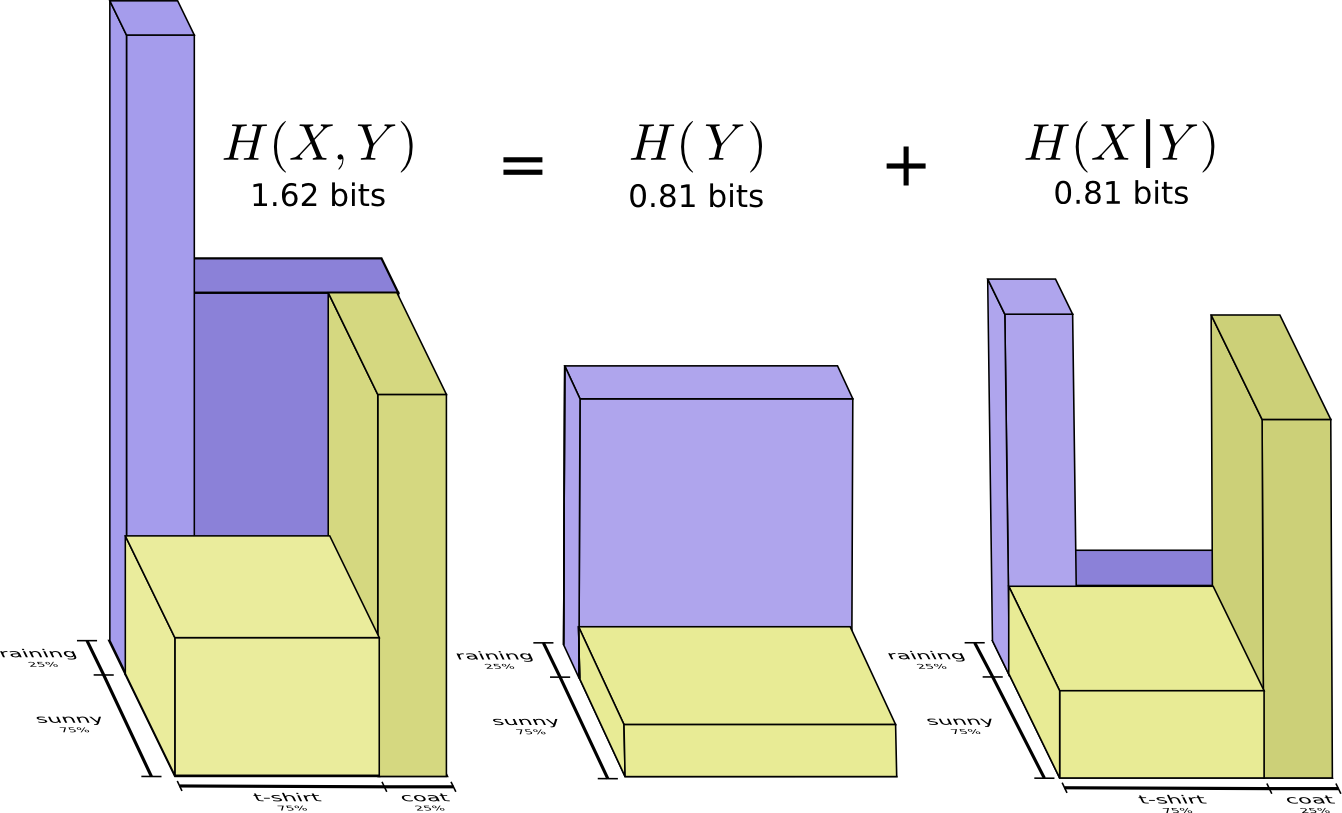
بدلاً من ذلك ، دعنا نركز على متغير مثل الطقس. نحن نعرف احتمالات الطقس المشمس والمطر. في كلتا الحالتين ، يمكننا النظر في الاحتمالات الشرطية. ما هو احتمال أن أرتدي قميصًا إذا كان مشمسًا؟ ما هي احتمالية ارتداء معطف واق من المطر إذا هطل المطر؟
مع احتمال 25٪ ، ستمطر. إذا هطل المطر ، فسأرتدي معطف واقٍ من المطر بنسبة 75٪. وبالتالي ، فإن احتمال هطول المطر وأرتدي معطف واق من المطر هو 25 ٪ من 75 ٪ ، وهو ما يقرب من 19 ٪. احتمال أن تمطر وأنا أرتدي معطف واق من المطر هو احتمال أن تمطر مضروبة في احتمال أن أرتدي معطف واق من المطر إذا كانت السماء تمطر. نكتبها مثل هذا:
p(المطر،المعطف)=p(المطر)⋅p(المعطف|المطر)
هذا مثال على واحدة من أكثر الهويات الأساسية لنظرية الاحتمالات:
p(x،y)=p(x)⋅p(y|x)
نحن نعامل التوزيع من خلال تقسيمه إلى منتج من جزأين. أولاً ، نلقي نظرة على احتمال أن يأخذ متغير واحد ، الطقس ، قيمة معينة. ثم نلقي نظرة على احتمال أن يأخذ متغير آخر ، ملابسي ، القيمة بسبب المتغير الأول.
الذي المتغير لتبدأ لا يهم. يمكن أن نبدأ بملابسي ، ثم نلقي نظرة على الطقس الناتج عن ذلك. قد يبدو هذا أقل سهولة لأننا نفهم أن هناك علاقة سببية بين الطقس تؤثر على ما أرتديه وليس العكس ... لكنها تعمل على أي حال!
لنلقِ نظرة على مثال. إذا اخترنا يوما عشوائيا ، مع احتمال 38 ٪ سأرتدي معطف واق من المطر. إذا علمنا أنني في معطف واق من المطر ، ما مدى احتمال سقوط المطر؟ أفضل ارتداء معطف واق من المطر في المطر بدلاً من الشمس ، لكن المطر في كاليفورنيا أمر نادر الحدوث ، وقد اتضح أنه مع احتمال هطول أمطار بنسبة 50٪. لذلك ، فإن احتمال أن تمطر وأرتدي معطف واق من المطر هو احتمال أن أرتدي معطف واق من المطر (38 ٪) ، مضروبا في احتمال أن تمطر إذا كنت أرتدي معطف واق من المطر (50 ٪) ، وهو حوالي 19 ٪.
ص ( ا ل م ط ر ، ا ل م ع ط ف ) = ص ( ا ل م ع ط ف ) ⋅ ص ( ا ل م ط ر | ا ل م ع ط ف )
هذا يعطينا طريقة ثانية لتصور نفس التوزيع الاحتمالي.
يرجى ملاحظة أن قيم التسمية لها معنى مختلف قليلاً عما كان في الرسم البياني السابق: أصبح القميص ومعطف المطر هما الآن احتمالات الحد ، واحتمال أن أرتدي هذه الملابس دون مراعاة الطقس. من ناحية أخرى ، هناك الآن علامتان للشمس والمطر ، لأن احتمالاتهما تعتمد على حقيقة أنني سأرتدي قميصًا أو معطف واق من المطر.
(ربما تكون قد سمعت عن نظرية بايز. يمكنك أن تتخيلها كطريقة للانتقال بين هاتين الطريقتين المختلفتين لتمثيل توزيع الاحتمالات!)
مربع: سيمبسون مفارقة
هل تقنيات التصور هذه لتوزيعات الاحتمال مفيدة حقًا؟ أعتقد ذلك! أبعد من ذلك بقليل ، نستخدمها لتصور نظرية المعلومات ، لكن في الوقت الحالي نستخدمها لدراسة مفارقة سيمبسون. مفارقة سيمبسون هي حالة إحصائية غير بديهية للغاية. من الصعب أن نفهم على مستوى بديهية. كتب مايكل نيلسن مقالاً ممتازاً بعنوان
Reinventing Explanation ، والذي يشرح المفارقة بعدة طرق. أريد أن أحاول القيام بذلك بنفسي ، باستخدام التقنيات التي طورناها في القسم السابق.
ويجري اختبار طريقتين لعلاج حصى الكلى. نصف المرضى يتلقون العلاج "أ" ، بينما النصف الآخر يتلقون العلاج "ب". المرضى الذين تلقوا العلاج "ب" كانوا أكثر عرضة للشفاء من أولئك الذين تلقوا العلاج "أ".
ومع ذلك ، كان المرضى الذين يعانون من حصى الكلى الصغيرة أكثر عرضة للشفاء إذا تلقوا العلاج أ. المرضى الذين يعانون من حصى الكلى الكبيرة في الكلى كانوا أكثر عرضة للتعافي إذا تلقوا العلاج A! كيف يمكن أن يكون هذا؟
جوهر المشكلة هو أن الدراسة لم تكن عشوائية بشكل صحيح. بين المرضى الذين يتلقون العلاج "أ" ، كان هناك المزيد من المرضى الذين يعانون من حصى الكلى الكبيرة ، وبين المرضى الذين يتلقون العلاج "ب" كان هناك المزيد من المصابين بحصوات الكلى الصغيرة.
كما اتضح ، فإن المرضى الذين يعانون من حصوات الكلى الصغيرة هم أكثر عرضة للتعافي بشكل عام.
لفهم هذا بشكل أفضل ، يمكننا الجمع بين المخططين السابقين. والنتيجة هي مخطط ثلاثي الأبعاد مع معدل الاسترداد مقسمة إلى حصوات الكلى الصغيرة والكبيرة.
الآن نرى أنه في حالة كل من الحجارة الصغيرة والكبيرة ، يكون العلاج A أفضل من العلاج B. العلاج B بدا أفضل فقط لأن المرضى الذين تم تطبيقه لديهم ، بشكل عام ، لديهم المزيد من فرص الشفاء!
رموز
الآن بعد أن أصبح لدينا طرق لتصور الاحتمالات ، يمكننا الغوص في نظرية المعلومات.
دعني أخبرك عن صديقي الخيالي ، بوب. بوب يحب الحيوانات كثيرا. يتحدث باستمرار عن الحيوانات. في الواقع ، يتحدث فقط أربع كلمات: "كلب" ، "قطة" ، "سمكة" و "طائر".
قبل أسبوعين ، على الرغم من حقيقة أن بوب كان من خيالي ، فقد انتقل إلى أستراليا. بالإضافة إلى ذلك ، قرر أنه يريد التواصل فقط في شكل ثنائي. تبدو جميع رسائلي (الخيالية) من بوب كما يلي:
للتواصل ، أحتاج أنا و Bob لإنشاء نظام ترميز - طريقة لعرض الكلمات في سلسلة من البتات.
لإرسال رسالة ، يستبدل بوب كل حرف (كلمة) بكلمة الشفرة المقابلة ، ثم يجمعها معًا لتشكيل سلسلة مشفرة.
رموز طول متغير
لسوء الحظ ، فإن خدمات الاتصالات في أستراليا الوهمية غالية الثمن. يجب أن أدفع 5 دولارات مقابل كل رسالة تلقيتها من بوب. هل ذكرت أن بوب يحب التحدث كثيرًا؟ من أجل عدم الإفلاس ، قررنا أنا وبوب معرفة ما إذا كان من الممكن تقليل متوسط طول الرسالة بطريقة أو بأخرى.
اتضح أن بوب لا نطق كل الكلمات على قدم المساواة في كثير من الأحيان. بوب يحب الكلاب كثيرا. يتحدث عن الكلاب في كل وقت. يتحدث في بعض الأحيان عن الحيوانات الأخرى - خاصة القط الذي يحب كلبه مطاردته - لكنه يتحدث عن الكلاب في الغالب. هنا رسم بياني لتكرار كلماته:
هذا مشجع. يستخدم الكود القديم كلمات تشفير من 2 بت ، بغض النظر عن عدد مرات استخدامها.
هناك طريقة جيدة لتصور هذا. في الرسم البياني التالي ، نستخدم المحور الرأسي لتصور احتمال كل كلمة
ع ( س ) ومحور أفقي لتصور طول كلمة المرور المقابلة
L ( س ) . يرجى ملاحظة أن المنطقة الناتجة هي متوسط طول كلمة الكود التي نرسلها ، في هذه الحالة 2 بت.
يمكن أن نكون أكثر ذكاءً ونجعل متغير الشفرة في الطول ، حيث تكون كلمات الشفرة للكلمات الشائعة أقصر. المشكلة هي أن هناك تنافسًا بين الأقزام الشفهية - مما يجعل الأمر أقصر ، فنحن مضطرون إلى جعل الآخرين لفترة أطول. لتقليل طول الرسالة ، من الناحية المثالية ، نود أن تكون جميع كلمات الشفرة قصيرة ، ولكن يجب استخدام أقصرها على نطاق واسع. وبالتالي ، تحتوي الشفرة الناتجة على كلمات مشفرة أقصر للكلمات الشائعة (على سبيل المثال ، "كلب") وكلمات مشفرة أطول للكلمات النادرة (على سبيل المثال ، "طائر").
دعونا تصور هذا مرة أخرى. يرجى ملاحظة أن كلمات المرور الأكثر شيوعًا تكون أقصر وأندرًا تكون أطول. نتيجة لذلك ، حصلنا على مساحة أصغر. هذا يتوافق مع طول الكلمة المتوقعة أقصر. متوسط طول كلمة المرور الآن 1.75 بت!
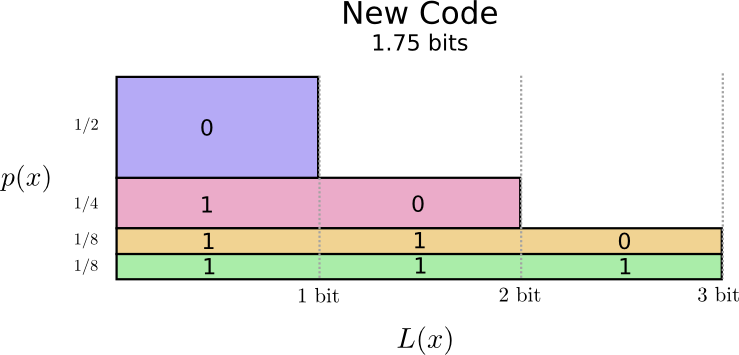
(قد تتساءل: لماذا لا تستخدم الرقم 1 على حدة ككلمة مرور؟ لسوء الحظ ، سيؤدي ذلك إلى غموض عند فك تشفير السلاسل المشفرة. سنتحدث أكثر عن هذا لاحقًا.)
اتضح أن هذا الكود هو الأفضل. لا يوجد رمز لهذا التوزيع من شأنه أن يعطينا متوسط طول كلمة مرور أقل من 1.75 بت.
هناك حد أساسي. يتطلب إرسال ما قيل ، أي حدث لهذا التوزيع ، أن نرسل ما معدله 1.75 بت على الأقل. بغض النظر عن مدى ذكائنا ، قد يكون من المستحيل تحقيق متوسط طول الرسالة. نحن نسمي هذا الحد الأساسي في
إنتروبيا التوزيع - سنناقشه بمزيد من التفاصيل أدناه.
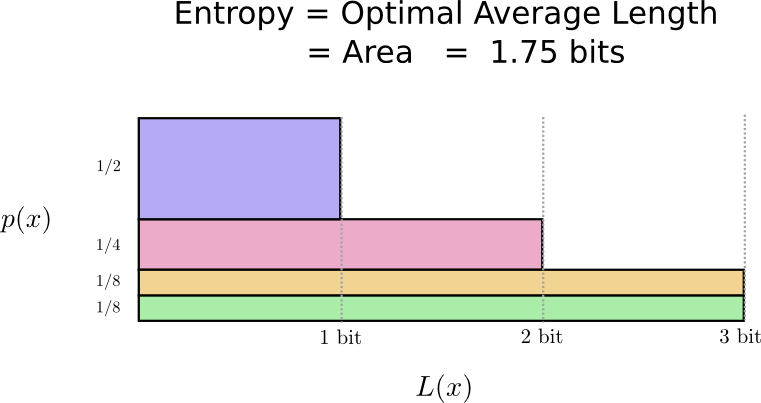
إذا كنا نريد أن نفهم هذا الحد ، فنحن بحاجة إلى فهم المفاضلة بين إبقاء بعض كلمات الشفرة قصيرة والبعض الآخر طويلاً. بمجرد اكتشاف هذا الأمر ، يمكننا معرفة أفضل أشكال أنظمة الترميز الممكنة.
كلمة المرور الفضاء
هناك اثنين من الكودات ذات طول 1 بت: 0 و 1. هناك أربعة من الكودرات ذات طول 2 بت: 00 ، 01 ، 10 و 11. كل بت تضيفه يتضاعف عدد كلمات الكود الممكنة.
نحن مهتمون برموز متغيرة الطول ، حيث تكون بعض كلمات الرموز أطول من غيرها. يمكن أن يكون لدينا مواقف بسيطة عندما يكون لدينا ثمانية كلمات مشفرة طولها 3 بتات. قد يكون هناك خلائط أكثر تعقيدًا ، على سبيل المثال ، اثنان من الكودات ذات طول 2 و 4 من كلمات الكود ذات الطول 3. ما الذي يقرر عدد كلمات الكود ذات الأطوال المختلفة التي يمكن أن تكون لدينا؟
تذكر أن بوب يحول رسالته إلى سلاسل مشفرة ، ويستبدل كل كلمة برمزه ويسلطها.
هناك سؤال دقيق يجب توخي الحذر عند إنشاء رموز متغيرة الطول. كيف يمكننا تقسيم السلسلة المشفرة مرة أخرى إلى كلمات رمز؟ عندما يكون لكل كلمات التكويد نفس الطول ، يكون ذلك سهلاً - ما عليك سوى تقسيم الخيط إلى أجزاء من ذلك الطول. ولكن نظرًا لوجود كلمات مشفرة بأطوال مختلفة ، نحتاج إلى الاهتمام بالمحتوى.
نريد كودنا أن يكون فك شفرة فريدة. ونحن لا نريدها أن تكون غامضة في تحديد كلمات المرور التي تشكل السلسلة المشفرة. إذا كان لدينا رمز خاص "نهاية كلمة الكود" ، فسيكون ذلك بسيطًا. لكننا لا نملك هذا - فنحن نرسل 0 و 1 فقط. نحتاج إلى أن نكون قادرين على إلقاء نظرة على تسلسل كلمات الكود وتحديد أين تنتهي كل منها.
من السهل جدًا إنشاء رموز لا يمكن فك تشفيرها بشكل لا لبس فيه. على سبيل المثال ، تخيل أن 0 و 01 كلاهما مصطلحان. إذن ، من غير الواضح ما هو الكود الأول في السطر 0100111 - يمكن أن يكون هذا أو ذاك! الخاصية التي نحتاجها هي أنه إذا رأينا كلمة مرور محددة ، فلا يجب تضمينها في كلمة مرور أخرى أطول. بمعنى آخر ، لا ينبغي أن يكون أي كلمة مشفرة بادئة لكلمة مرور أخرى. وهذا ما يسمى خاصية البادئة ، والرموز التي تطيعها تسمى
رموز البادئة .
هناك طريقة مفيدة لتمثيل ذلك وهي أن كل كلمة سرية تتطلب تضحيات من فضاء كلمات مشفرة محتملة. إذا أخذنا كلمة الكود 01 ، فإننا نفقد القدرة على استخدام أي كلمات كود لها بادئة. لم يعد بإمكاننا استخدام 010 أو 011010110 بسبب الغموض - فقدناها.
نظرًا لأن ربع جميع الكلمات المشفرة يبدأ في 01 ، فقد تبرعنا بربع جميع الكلمات المشفرة المحتملة. هنا هو السعر الذي ندفعه مقابل حقيقة أن لدينا كلمة مشفرة واحدة بطول 2 بت فقط! في المقابل ، فإن هذه التضحية تعني أنه ينبغي أن تكون جميع كلمات الشفرة الأخرى أطول قليلاً. هناك دائمًا نوع من التسوية بين أطوال الكودورات المختلفة. يتطلب كلمة مشفرة قصيرة منك التضحية بمعظم مساحة كلمات التشفير المحتملة ، مما يمنع اختصار كلمات مشفرة أخرى. ما نحتاج إلى معرفته هو كيفية التسوية بشكل صحيح!
الترميز الأمثل
يمكنك التفكير في الأمر على أنه ميزانية محدودة يمكنك إنفاقها على الحصول على كلمات مختصرة. نحن ندفع ثمن كلمة مشفرة واحدة ، ونضحي بجزء من كلمات مشفرة ممكنة.
تكلفة شراء كلمة مرور ذات طول 0 هي 1 - جميع كلمات البرمجة الممكنة - إذا كنت ترغب في الحصول على كلمة مرور ذات طول 0 ، فلا يمكن أن يكون لديك أي كلمة مرور أخرى. تكلفة كلمة مشفرة بطول 1 ، على سبيل المثال ، "0" ، هي 1/2 ، لأن نصف كلمات الترميز الممكنة تبدأ بـ "0". تبلغ تكلفة كلمة مرور طولها 2 ، على سبيل المثال "01" ، 1/4 ، لأن ربع جميع كلمات المرور الممكنة يبدأ بـ "01". بشكل عام ، تنخفض تكلفة الكودات بشكل كبير مع زيادة طول الكود.
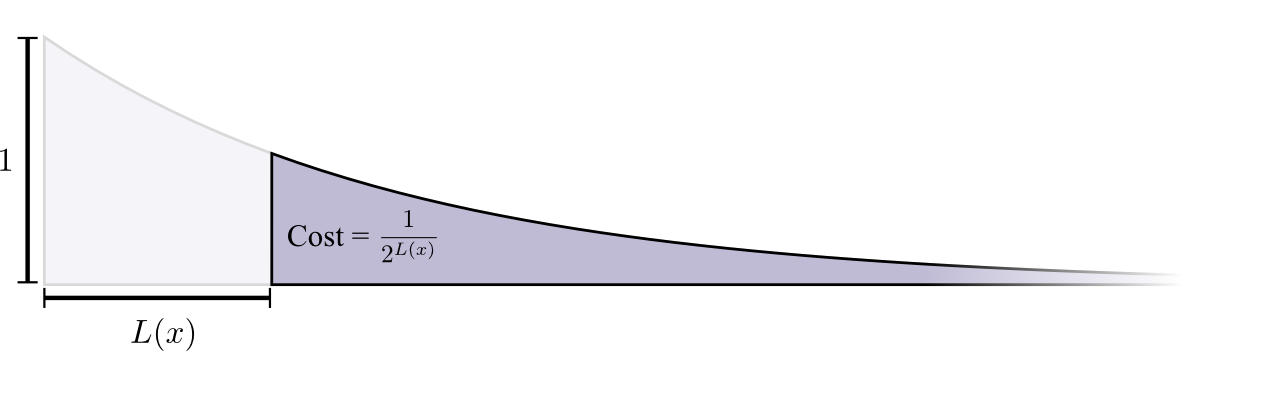
يرجى ملاحظة أنه إذا انخفضت التكلفة كعارض (عيني) ، فهذا يمثل ارتفاعًا ومساحة على حد سواء! (
يستخدم المثال الأس مع الأساس 2 حيث تكون هذه الحقيقة غير صحيحة ، ولكن يمكنك التبديل إلى الأس الطبيعي ، الذي يبسط الاختبار بصريًا )
.نحتاج إلى كلمات مصورة قصيرة لأننا نريد تقليل متوسط أطوال الرسائل. يزيد كل كلمة مرور من متوسط طول الرسالة باحتمال أن تضاعف هذه الكلمة طولها. على سبيل المثال ، إذا احتجنا إلى إرسال كلمة مرور 4 بتات طولها 50٪ من الوقت ، فسيكون متوسط طول الرسالة لدينا 2 بت أطول من إذا لم نرسل هذا الكود. يمكننا أن نتخيل هذا كمستطيل.
ترتبط هاتان القيمتان بطول كلمة المرور. السعر الذي ندفعه يحدد طول كلمة الكود. يحدد طول كلمة المرور مقدار ما يضيفه إلى متوسط طول الرسالة. يمكننا أن نتخيلهم معا مثل هذا.

تعمل الكلمات الرئيسية القصيرة على تقليل متوسط طول الرسالة ، ولكنها باهظة الثمن ، بينما تزيد الكلمات الرئيسية الطويلة من متوسط طول الرسالة ، ولكنها رخيصة.

ما هي أفضل طريقة لاستخدام ميزانيتنا المحدودة؟ كم يجب أن ننفق على كلمة مرور لكل حدث؟
كما يريد الشخص أن يستثمر أكثر في الأدوات التي يستخدمها بانتظام ، فإننا نريد أن ننفق أكثر على كلمات الكود الشائعة الاستخدام. هناك طريقة طبيعية خاصة للقيام بذلك: توزيع ميزانيتنا بما يتناسب مع عدد مرات حدوث الحدث. لذلك ، إذا حدث هذا الحدث في 50 ٪ من الحالات ، فإننا ننفق 50 ٪ من ميزانيتنا على شراء كلمة مرور قصيرة لذلك. لكن إذا حدث هذا الحدث بنسبة 1٪ فقط من الوقت ، فنحن ننفق 1٪ فقط من ميزانيتنا ، لأننا لسنا قلقين جدًا على طول كلمة الشفرة.
هذا شيء طبيعي ، لكن هل هو الأمثل؟ هذا صحيح ، وسأثبت ذلك!
الدليل التالي واضح ويجب فهمه ، لكن الأمر سيستغرق بعض العمل لإتمامه ، وهذا بالتأكيد الجزء الأصعب من هذا المقال. يمكن للقراء تخطيها بأمان ، وقبول الحقيقة دون إثبات والمتابعة إلى القسم التالي.دعونا نلقي نظرة على مثال محدد حيث نحتاج إلى معرفة أي حدثين ممكنين حدثا. حدثعلى الذهابع ( أ ) الوقت ، والحدثب يحدثع ( ب ) الوقت. نحن نخصص ميزانيتنا بالطريقة الطبيعية الموضحة أعلاه ، الإنفاقع ( أ ) ميزانية الكودود القصيرة الخاصة بنال و
ع ( ب ) لتلقي كلمة قصيرةب .
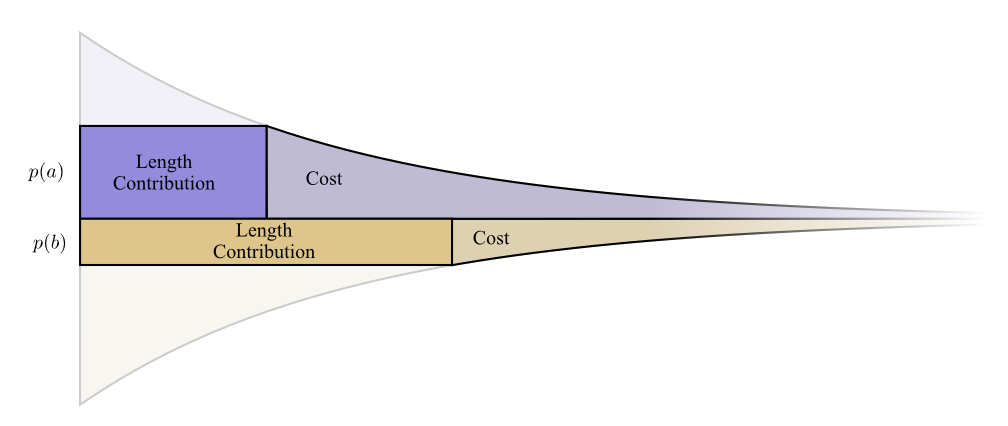 حدود التكلفة وطول خط يصل بشكل جميل. هل هذا يعني أي شيء؟فكر في ما يحدث لمساهمة التكلفة والطول إذا قمنا بتغيير طول كلمة المرور قليلاً. إذا قمنا بزيادة طول كلمة المرور قليلاً ، فإن مساهمة طول الرسالة ستزداد بما يتناسب مع ارتفاعها على الحدود ، وستنخفض التكلفة بما يتناسب مع ارتفاعها على الحدود.
حدود التكلفة وطول خط يصل بشكل جميل. هل هذا يعني أي شيء؟فكر في ما يحدث لمساهمة التكلفة والطول إذا قمنا بتغيير طول كلمة المرور قليلاً. إذا قمنا بزيادة طول كلمة المرور قليلاً ، فإن مساهمة طول الرسالة ستزداد بما يتناسب مع ارتفاعها على الحدود ، وستنخفض التكلفة بما يتناسب مع ارتفاعها على الحدود. وبالتالي ، فإن تكلفة إنشاء كلمة مرور أقصر هيع ( أ )
وبالتالي ، فإن تكلفة إنشاء كلمة مرور أقصر هيع ( أ ) .
نحن لسنا مهتمين بنفس القدر بطول كل كلمة مرور ، فهم يهمنا بما يتناسب مع عدد المرات التي نستخدمها فيها. في حالةو - هوع ( أ ) .
مكاسبنا من جعل الكودورد أقصر قليلاً متناسبة ع ( أ ) .
ومن المثير للاهتمام ، كلا المشتقات هي نفسها. هذا يعني أن ميزانيتنا المبدئية لها ميزة مثيرة للاهتمام: إذا كان لديك أموال أكثر بقليل ، فسيكون من الجيد بنفس القدر الاستثمار في تقليل أي كلمة مرور. ما يهمنا حقًا هو نسبة الفائدة / التكلفة - وهذا ما يقرر ما يجب أن نستثمر فيه أكثر. في هذه الحالة ، فإن النسبةع ( أ )ع ( أ ) ، أي ما يعادل واحد. لا تعتمد على قيمة p (a) - إنها تساوي دائمًا الوحدة. ويمكننا تطبيق الحجة نفسها على أحداث أخرى. الفائدة / التكلفة هي دائما واحدة ، لذلك فمن المنطقي أن تستثمر أكثر قليلا في أي من الأحداث. فيما يتعلق بالحد الأدنى ، فإن تغيير الميزانية لا معنى له. لكن هذا ليس دليلا على أن هذه هي أفضل ميزانية. لإثبات ذلك ، سننظر في ميزانية مختلفة حيث ننفق أكثر قليلاً على كلمة مرور واحدة على حساب أخرى. سوف ننفق على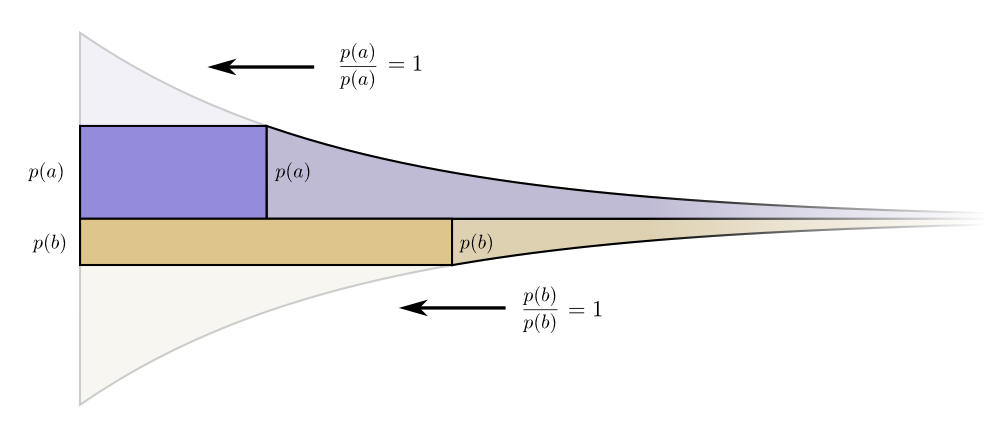 ε أقل علىب ، وإضافة هذاϵ الحدثل
ε أقل علىب ، وإضافة هذاϵ الحدثل .
يجعل كلمة مشفرة ل هو أقصر قليلا ، وكلمة رمز لب أطول قليلا. الآن سعر شراء كلمة مرور أقصر لأ متساوp ( a ) + ϵ ، وسعر شراء كلمة المرور الأقصر لـب متساوص ( ب ) - ϵ .
لكن الفوائد هي نفسها. هذا يؤدي إلى حقيقة أن نسبة التكلفة / الفائدة لعملية الشراءو إرادةع ( أ )p ( a ) + ϵ ، وهو أقل من الوحدة. من ناحية أخرى ، فإن نسبة التكلفة / الفائدة للشراء ب هيع ( ب )p ( b ) + ϵ ، وهو أكثر من واحد. الأسعار لم تعد متوازنة.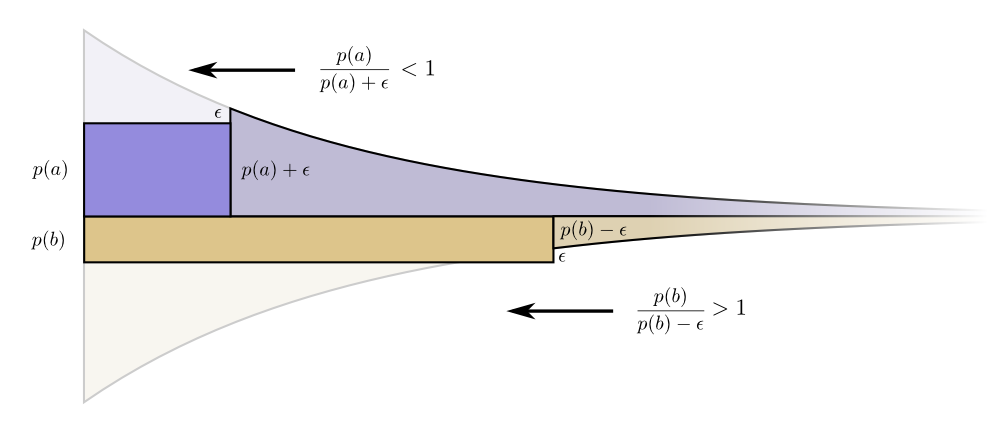 ب صفقة أفضل منل
ب صفقة أفضل منل .
يصرخ المستثمرون: "شراء ب !
بيع و ! »ونحن نفعل ذلك ونعود إلى خطتنا الميزانية الأصلية. يمكن تحسين جميع الميزانيات من خلال العودة إلى خطتنا الأصلية. لم تكن الميزانية الأولية - الاستثمار في كل كلمة مرور متناسبة مع عدد المرات التي نستخدمها فيها - خيارًا طبيعيًا فحسب ، بل كانت الخيار الأمثل. (يعمل دليلنا فقط على اثنين من الكودات ، ويمكن بسهولة تعميمه على عدد أكبر.)(ربما لاحظ القارئ اليقظ أنه في حالة وجود ميزانية مثالية ، قد تظهر الرموز التي تكون فيها كلمات الشفرة كسرية في الطول. ماذا يعني هذا؟ نرى لاحقًا ، هناك شعور حقيقي في إرسال كلمات الكسور عندما نرسل الكثير منها في نفس الوقت!)ملاحظة: يكرس الاستمرارية للإنتروبيا ، والإنتروبيا ، والمعلومات المتبادلة ، والبتات الكسرية ، وغيرها من الأشياء المثيرة للاهتمام.