أساسيات التعلم العميق على سبيل المثال من التصحيح التلقائي ، الجزء رقم 1

إذا قرأت التدريب على أجهزة الترميز التلقائي على موقع keras.io ، فإن إحدى الرسائل الأولى هناك شيء من هذا القبيل: في الممارسة العملية ، لا يتم استخدام برامج الترميز التلقائي أبدًا ، ولكن غالبًا ما يتم التحدث عنها في الدورات التدريبية ويأتي الأشخاص حولها ، لذلك قررنا كتابة البرنامج التعليمي الخاص بنا حولهم:

إدعائهم الرئيسي إلى الشهرة يأتي من أن يتم عرضه في العديد من دروس التعلم الآلي التمهيدية المتاحة على الإنترنت. كنتيجة لذلك ، يحب الكثير من القادمين الجدد إلى الميدان محررات التشفير التلقائي ولا يمكنهم الحصول على ما يكفي منهم. هذا هو السبب في وجود هذا البرنامج التعليمي!

ومع ذلك ، فإن إحدى المهام العملية التي يمكن تطبيقها على نفسه هي البحث عن الحالات الشاذة ، وأنا شخصياً احتاجها في المشروع المسائي.

على الإنترنت ، هناك الكثير من البرامج التعليمية على أجهزة الترميز التلقائي ، ماذا عن كتابة واحدة أخرى؟ حسنًا ، بصراحة ، كانت هناك عدة أسباب لذلك:

• كان هناك شعور في الواقع أن البرامج التعليمية كانت حوالي 3 أو 4 ، تم إعادة كتابة الباقي بكلماتهم الخاصة ؛
• كل شيء تقريبًا - على MNIST'e الذي طالت مع الصور 28 × 28 ؛
• في رأيي المتواضع - إنهم لا يطورون حدسًا حول كيفية عمل كل هذا ، ولكنهم ببساطة يعرضون التكرار ؛
• وأهم عامل - شخصيا ، عندما استبدلت MNIST بمجموعة البيانات الخاصة بي - توقف كل شيء بغباء عن العمل .

ما يلي يصف طريقي الذي المخاريط محشوة. إذا أخذت أيًا من النماذج المسطحة (غير التلافيفية) المقترحة من مجموعة البرامج التعليمية وقمت بنسخها بغباء ، فلن ينجح شيء بشكل مدهش. الغرض من المقالة هو فهم السبب ، وعلى ما يبدو لي ، الحصول على نوع من الفهم الحدسي لكيفية عمل كل هذا.

أنا لست متخصصًا في التعلم الآلي وأستخدم الأساليب التي اعتدت عليها في العمل اليومي. بالنسبة لعلماء البيانات ذوي الخبرة ، من المحتمل أن تكون هذه المقالة كاملة ، ولكن بالنسبة للمبتدئين ، يبدو لي أنه قد يتم طرح شيء جديد.

لنبدأ. لدي مجموعة من 4000 صورة بالأبيض والأسود 64 × 64 بكسل ، تبدو كما يلي:

فقط بعض الخطوط على خلفية سوداء ، وفي صورة 64 × 64 يتم ملء حوالي 2 ٪ من النقاط. إذا نظرت إلى الكثير من الصور ، بالطبع ، اتضح أن معظم الخطوط متشابهة إلى حد كبير.

لن أخوض في تفاصيل كيفية تحميل مجموعة البيانات ومعالجتها ، لأن الغرض من المقالة ، مرة أخرى ، ليس هذا. فقط عرض قطعة مخيفة من التعليمات البرمجية.

# only for google colab %tensorflow_version 2.x import tensorflow as tf import numpy as np import matplotlib.pyplot as plt import os import zipfile import datetime import tensorflow_addons as tfa BATCH_SIZE = 128 AUTOTUNE=tf.data.experimental.AUTOTUNE def load_image(fpath): img_raw = tf.io.read_file(fpath) img = tf.io.decode_png(img_raw, channels=1, dtype=tf.uint8) return tf.image.convert_image_dtype(img, dtype=tf.float32) ## for splitting test/train def is_test(x, y): return x % 4 == 0 def is_train(x, y): return not is_test(x,y) ## for image augmentation def random_flip_flop(img): return tf.image.random_flip_left_right(img) def transform_aug(shift_val): def random_transform(img): return tfa.image.translate(img,tf.random.uniform([2], -1*shift_val, shift_val)) return random_transform def prepare_for_training(ds, cache=True, shuffle_buffer_size=1000, transform=0, flip=False): if cache: if isinstance(cache, str): ds = ds.cache(cache) else: ds = ds.cache() ds = ds.shuffle(buffer_size=shuffle_buffer_size) if transform != 0: ds = ds.map(transform_aug(transform)) if flip: ds = ds.map(random_flip_flop) ds = ds.repeat() ds = ds.batch(BATCH_SIZE) ds = ds.prefetch(buffer_size=AUTOTUNE) return ds def prepare_input_output(x): return (x, x) list_ds = tf.data.Dataset.list_files("/content/planes64/*") imgs_df = list_ds.map(load_image) train = imgs_df.enumerate().filter(is_train).map(lambda x,y: y) train_ds = prepare_for_training(train, transform=10, flip=True) train_ds = train_ds.map(prepare_input_output) val = imgs_df.enumerate().filter(is_test).map(lambda x, y: y) val_ds = val.map(prepare_input_output).batch(BATCH_SIZE, drop_remainder=True) 

هنا ، على سبيل المثال ، هو النموذج الأول المقترح مع keras.io ، والذي عملوا عليه وتدريبهم على mnist:

 # this is the size of our encoded representations encoding_dim = 32 # 32 floats -> compression of factor 24.5, assuming the input is 784 floats # this is our input placeholder input_img = Input(shape=(784,)) # "encoded" is the encoded representation of the input encoded = Dense(encoding_dim, activation='relu')(input_img) # "decoded" is the lossy reconstruction of the input decoded = Dense(784, activation='sigmoid')(encoded) 

في حالتي ، يتم تعريف النموذج مثل هذا:

 model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64/10, activation='relu')) model.add(tf.keras.layers.Dense(64*64, activation="sigmoid")) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1))) 

هناك اختلافات طفيفة أقوم بتسويتها وأعيد تشكيلها مباشرة في النموذج ، وأنني "لا ضغط" 25 مرة ، ولكن فقط 10. لا ينبغي أن يؤثر هذا على أي شيء.

كخسارة دالة - يعني الخطأ التربيعي ، المحسن ليس أساسيا ، دع آدم. فيما يلي ، نقوم بتدريب 20 عصور ، 100 خطوة لكل حقبة.

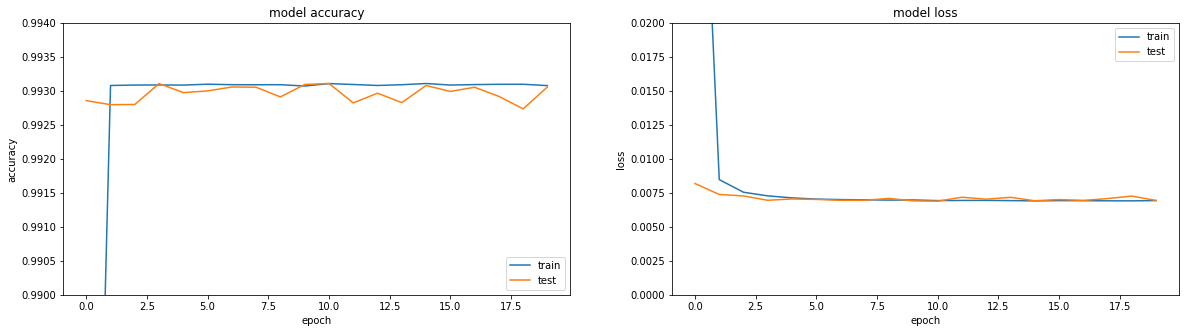
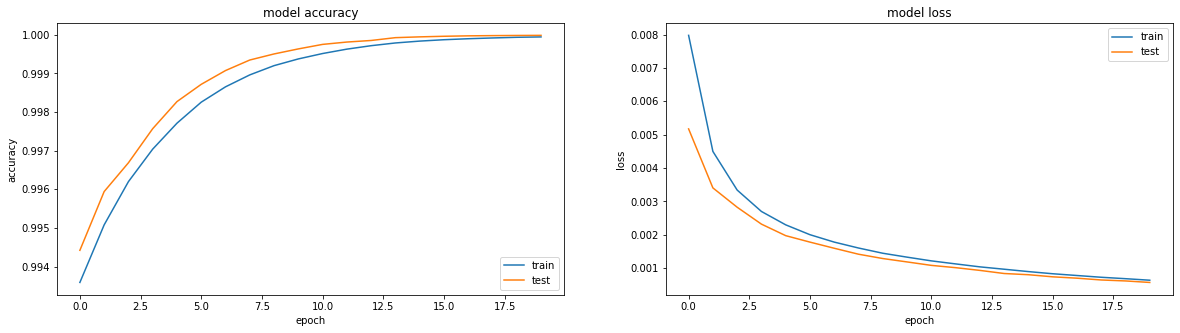
إذا نظرت إلى المقاييس - كل شيء على النار. الدقة == 0.993. إذا نظرت إلى جداول التدريب - كل شيء محزن بعض الشيء ، فنحن نصل إلى هضبة في المنطقة من العصر الثالث.

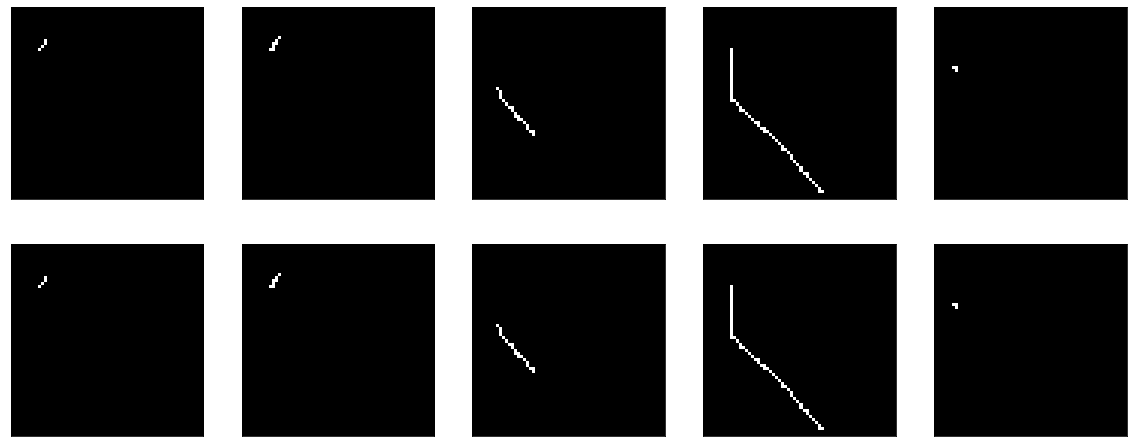
حسنًا ، إذا نظرت مباشرةً إلى نتيجة التشفير ، فستحصل على صورة حزينة بشكل عام (الأصل في الأعلى ، وتكون نتيجة فك التشفير أدناه):

بشكل عام ، عندما تحاول معرفة سبب عدم عمل شيء ما ، فإن اتباع منهج جيد بما فيه الكفاية لتقسيم جميع الوظائف إلى كتل كبيرة والتحقق من كل منها بمعزل عن غيرها. لذلك دعونا نفعل ذلك.

في الأصل من البرنامج التعليمي - يتم توفير البيانات المسطحة لإدخال نموذج ويتم أخذها في الإخراج. لماذا لا تحقق من أفعالي على تتسطح وإعادة تشكيل. إليكم نموذج عدم المرجع:

 model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1))) 

النتيجة:

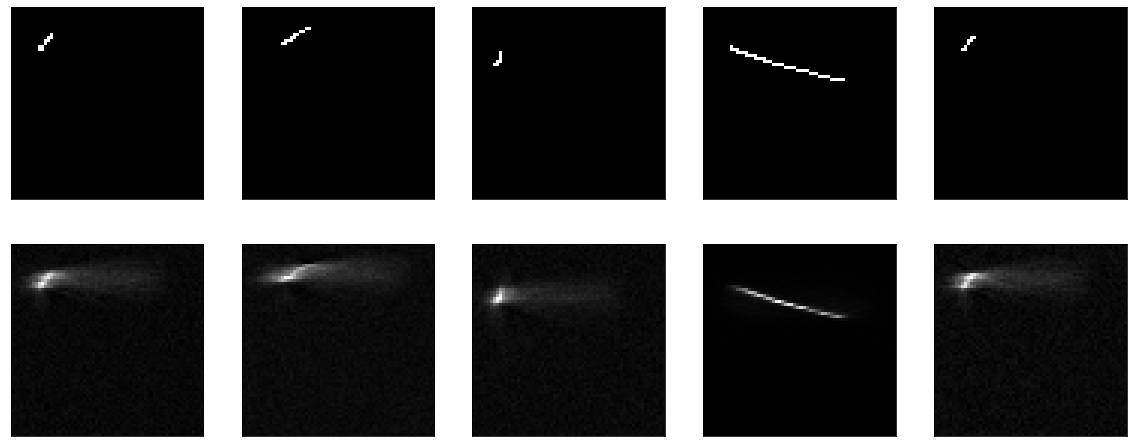
لا يوجد شيء لتدريسه هنا. حسنًا ، في الوقت نفسه ، أثبت أن وظيفة التصور الخاصة بي تعمل أيضًا.

بعد ذلك ، حاول أن تجعل النموذج ليس بلا مرجع ، ولكن أغبى قدر الإمكان - فقط قم بقص طبقة الضغط ، اترك طبقة واحدة بحجم المدخلات. كما يقولون في جميع البرامج التعليمية ، يقولون ، من المهم جدًا أن يتعلم النموذج الخاص بك الميزات ، وليس فقط وظيفة الهوية. حسنًا ، هذا هو بالضبط ما سنحاول الحصول عليه ، دعنا فقط نمرر الصورة الناتجة إلى المخرجات.

 model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, activation="sigmoid")) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1))) 

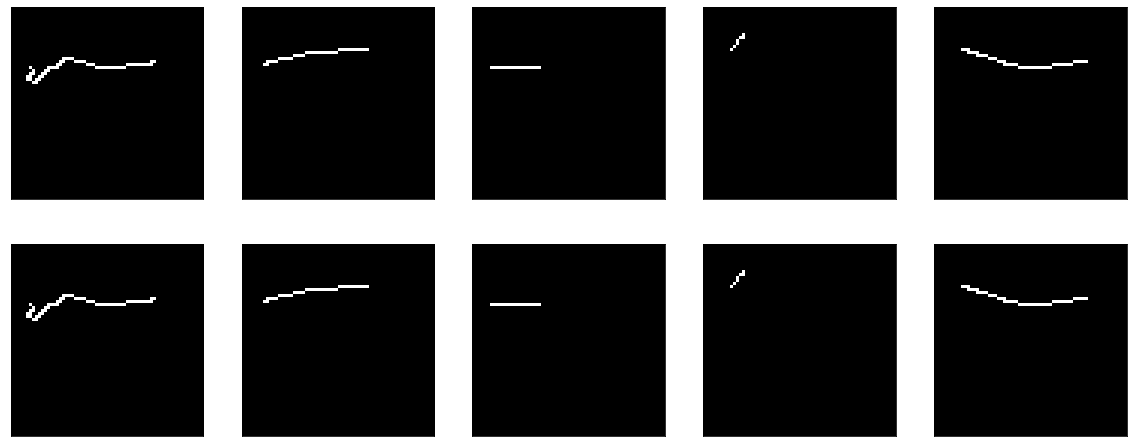
إنها تتعلم شيئًا ما ، = = 0.995 ، وتتعثر مرة أخرى في هضبة.

لكن بشكل عام ، من الواضح أنها لا تنجح بشكل جيد. على أي حال - ما الذي يجب تعلمه هناك ، مرر مدخل المخرج وهذا كل شيء.

إذا كنت تقرأ وثائق keras حول الطبقات الكثيفة ، فهي تصف ما يفعلونه: output = activation(dot(input, kernel) + bias)
لكي يتزامن الإخراج مع المدخلات ، هناك شيئان بسيطان يكفيان: التحيز = 0 و kernel - مصفوفة الهوية (من المهم عدم ترك المصفوفة مليئة بوحدات هنا - هذه أشياء مختلفة تمامًا). لحسن الحظ ، يمكن إجراء كل من هذا وذاك بسهولة تامة من الوثائق الخاصة Dense نفسها.

 model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, activation = "sigmoid", use_bias=False, kernel_initializer = tf.keras.initializers.Identity())) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1))) 

لأن وضعنا الوزن على الفور ، ثم لا يمكنك تعلم أي شيء - إنه جيد على الفور:

ولكن إذا بدأت التدريب ، فإنه يبدأ ، للوهلة الأولى ، بشكل مفاجئ - يبدأ النموذج بدقة == 1.0 ، لكنه ينهار بسرعة.
تقييم النتيجة قبل التدريب: 8/Unknown - 1s 140ms/step - loss: 0.2488 - accuracy: 1.0000[0.24875330179929733, 1.0] . التعليم:

 Epoch 1/20 100/100 [==============================] - 6s 56ms/step - loss: 0.1589 - accuracy: 0.9990 - val_loss: 0.0944 - val_accuracy: 0.9967 Epoch 2/20 100/100 [==============================] - 5s 51ms/step - loss: 0.0836 - accuracy: 0.9964 - val_loss: 0.0624 - val_accuracy: 0.9958 Epoch 3/20 100/100 [==============================] - 5s 50ms/step - loss: 0.0633 - accuracy: 0.9961 - val_loss: 0.0470 - val_accuracy: 0.9958 Epoch 4/20 100/100 [==============================] - 5s 48ms/step - loss: 0.0520 - accuracy: 0.9961 - val_loss: 0.0423 - val_accuracy: 0.9961 Epoch 5/20 100/100 [==============================] - 5s 48ms/step - loss: 0.0457 - accuracy: 0.9962 - val_loss: 0.0357 - val_accuracy: 0.9962 

نعم ، وليس الأمر واضحًا للغاية ، لدينا بالفعل نموذج مثالي - تظهر الصورة 1 في 1 ، وتظهر الخسارة (يعني الخطأ التربيعي) 0.25 تقريبًا.

هذا ، بالمناسبة ، سؤال متكرر على المنتديات - الخسارة آخذة في الانخفاض ، ولكن الدقة لا تتزايد ، كيف يمكن أن يكون هذا؟
هنا تجدر الإشارة مرة أخرى إلى تعريف الطبقة الكثيفة: output = activation(dot(input, kernel) + bias) وكلمة التنشيط المذكورة فيها ، والتي تجاهلتها بنجاح أعلاه. مع الأوزان من مصفوفة الهوية وبدون تحيز ، نحصل على output = activation(input) .

في الواقع ، يشار بالفعل إلى وظيفة التنشيط في الكود المصدري لدينا ، السيني ، وأنا نسختها بغباء وهذا كل شيء. وفي البرامج التعليمية ينصح باستخدامه في كل مكان. ولكن عليك أن تعرف ذلك.

بالنسبة للمبتدئين ، يمكنك قراءة ما يكتبونه حوله في الوثائق: The sigmoid activation: (1.0 / (1.0 + exp(-x))) . هذا شخصياً لا يخبرني بأي شيء ، لأنني لست فانتومو مرة واحدة لبناء مثل هذه الرسوم البيانية في رأسي.
ولكن يمكنك البناء باستخدام الأقلام:

 import matplotlib.ticker as plticker range_tensor = tf.range(-4, 4, 0.01, dtype=tf.float32) fig, ax = plt.subplots(1,1) plt.plot(range_tensor.numpy(), tf.keras.activations.sigmoid(range_tensor).numpy()) ax.grid(which='major', linestyle='-', linewidth='0.5', color='red') ax.grid(which='minor', linestyle=':', linewidth='0.5', color='black') ax.yaxis.set_major_locator(plticker.MultipleLocator(base=0.5) ) plt.minorticks_on() 

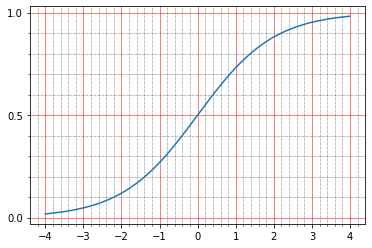
وهنا يتضح أنه عند الصفر يأخذ السيني على القيمة 0.5 ، وفي الوحدة - حوالي 0.73. والنقاط التي لدينا هي إما أسود (0.0) أو أبيض (1.0). لذلك اتضح أن خطأ التربيع يعني أن وظيفة الهوية تظل غير صفرية.

يمكنك حتى النظر إلى الأقلام ، وهنا سطر واحد من الصورة الناتجة:

 array([0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.7310586, 0.7310586, 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 ], dtype=float32) 

وهذا كل شيء رائع ، في الواقع ، لأن العديد من الأسئلة تظهر في وقت واحد:

• لماذا لم يكن هذا مرئيًا في التصور أعلاه؟
• لماذا إذن = = 1.0 ، لأن الصور الأصلية هي 0 و 1.

مع التصور ، كل شيء بسيط بشكل مدهش. لعرض الصور ، استخدمت matplotlib: plt.imshow(res_imgs[i][:, :, 0]) . وكالعادة ، إذا ذهبت إلى الوثائق ، فسيتم كتابة كل شيء هناك: The Normalize instance used to scale scalar data to the [0, 1] range before mapping to colors using cmap. By default, a linear scaling mapping the lowest value to 0 and the highest to 1 is used. The Normalize instance used to scale scalar data to the [0, 1] range before mapping to colors using cmap. By default, a linear scaling mapping the lowest value to 0 and the highest to 1 is used. أي وضعت المكتبة طبيعتي بعناية 0.5 و 0.73 في النطاق من 0 إلى 1. غير الكود:

 plt.imshow(res_imgs[i][:, :, 0], norm=matplotlib.colors.Normalize(0.0, 1.0)) 

وهنا السؤال بدقة. بادئ ذي بدء - من العادة ، نذهب إلى الوثائق ، وقراءة ل tf.keras.metrics.Accuracy وهناك يبدو أنهم يكتبون مفهومة:

 For example, if y_true is [1, 2, 3, 4] and y_pred is [0, 2, 3, 4] then the accuracy is 3/4 or .75. 

لكن في هذه الحالة ، كان ينبغي أن تكون دقتنا صفرًا. وكنتيجة لذلك ، دفنت نفسي في المصدر وهذا واضح تمامًا لنفسي:

  When you pass the strings 'accuracy' or 'acc', we convert this to one of `tf.keras.metrics.BinaryAccuracy`, `tf.keras.metrics.CategoricalAccuracy`, `tf.keras.metrics.SparseCategoricalAccuracy` based on the loss function used and the model output shape. We do a similar conversion for the strings 'crossentropy' and 'ce' as well. 

علاوة على ذلك ، في الوثائق الموجودة على الموقع لسبب ما ، هذه الفقرة ليست في وصف .compile .

إليك جزء من التعليمات البرمجية من https://github.com/tensorflow/tensorflow/blob/66c48046f169f3565d12e5fea263f6d731f9bfd2/tensorflow/python/keras/engine/compile_utils.py

 y_t_rank = len(y_t.shape.as_list()) y_p_rank = len(y_p.shape.as_list()) y_t_last_dim = y_t.shape.as_list()[-1] y_p_last_dim = y_p.shape.as_list()[-1] is_binary = y_p_last_dim == 1 is_sparse_categorical = ( y_t_rank < y_p_rank or y_t_last_dim == 1 and y_p_last_dim > 1) if metric in ['accuracy', 'acc']: if is_binary: metric_obj = metrics_mod.binary_accuracy elif is_sparse_categorical: metric_obj = metrics_mod.sparse_categorical_accuracy else: metric_obj = metrics_mod.categorical_accuracy 

y_t هي y_true ، أو الإخراج المتوقع ، y_p متوقع y_ ، أو النتيجة المتوقعة.
لدينا تنسيق البيانات: shape=(64,64,1) ، لذلك اتضح أن الدقة تعتبر ثنائية الدقة. الفائدة من أجل كيفية النظر فيها:

 def binary_accuracy(y_true, y_pred, threshold=0.5): threshold = math_ops.cast(threshold, y_pred.dtype) y_pred = math_ops.cast(y_pred > threshold, y_pred.dtype) return K.mean(math_ops.equal(y_true, y_pred), axis=-1) 

من المضحك أننا محظوظون هنا - افتراضيًا ، كل شيء يعتبر وحدة تزيد عن 0.5 و 0.5 وأقل - صفر. لذلك تأتي الدقة مئة في المئة لنموذج هويتنا ، على الرغم من أن الأرقام الموجودة في الواقع ليست على الإطلاق. حسنًا ، من الواضح أننا إذا أردنا ذلك بالفعل ، فيمكننا تصحيح العتبة وتقليل الدقة إلى الصفر ، على سبيل المثال ، ليست هناك حاجة إلى ذلك بالفعل. هذا مقياس ، لا يؤثر على التدريب ، ما عليك سوى فهم أنه يمكنك حسابه بألف طرق مختلفة والحصول على مؤشرات مختلفة تمامًا. على سبيل المثال ، يمكنك سحب العديد من المقاييس باستخدام الأقلام ونقل بياناتنا إليهم:

 m = tf.keras.metrics.BinaryAccuracy() m.update_state(x_batch, res_imgs) print(m.result().numpy()) 

سوف تعطينا 1.0 .

و هنا

 m = tf.keras.metrics.Accuracy() m.update_state(x_batch, res_imgs) print(m.result().numpy()) 

سوف تعطينا 0.0 على نفس البيانات.

بالمناسبة ، يمكن استخدام نفس الكود للعب مع وظائف الخسارة وفهم كيفية عملها. إذا كنت تقرأ البرامج التعليمية على أجهزة الترميز التلقائي ، فإنهم يقترحون بشكل أساسي استخدام إحدى وظيفتي الخسارة: إما يعني الخطأ التربيعي أو "binary_crossentropy". يمكنك أيضا أن ننظر إليها في نفس الوقت.

أنا أذكركم بأنني قدمت بالفعل نماذج mse أجل mse :

 8/Unknown - 2s 221ms/step - loss: 0.2488 - accuracy: 1.0000[0.24876083992421627, 1.0] 

أي خسارة = 0.2488. دعونا نرى لماذا هذا. يبدو لي شخصيا أنه أبسط وأكثر قابلية للفهم: يتم طرح الفرق بين y_true و y_predict بكسل في بكسل ، يتم تربيع كل نتيجة ، ثم يتم البحث في المتوسط.

 tf.keras.backend.mean(tf.math.squared_difference(x_batch[0], res_imgs[0])) 

وفي الإخراج:

 <tf.Tensor: shape=(), dtype=float32, numpy=0.24826494> 

هنا الحدس بسيط للغاية - غالبية البيكسلات الفارغة ، ينتج النموذج 0.5 ، ويحصل على 0.25 - فرق التربيعية بالنسبة لهم.

مع crossenttrtopy الثنائية ، الأمور أكثر تعقيدًا قليلاً ، وهناك مقالات كاملة حول كيفية عمل ذلك ، ولكن شخصياً كان من الأسهل دائمًا قراءة المصادر ، ويبدو الأمر كما يلي:

  if from_logits: return nn.sigmoid_cross_entropy_with_logits(labels=target, logits=output) if not isinstance(output, (ops.EagerTensor, variables_module.Variable)): output = _backtrack_identity(output) if output.op.type == 'Sigmoid': # When sigmoid activation function is used for output operation, we # use logits from the sigmoid function directly to compute loss in order # to prevent collapsing zero when training. assert len(output.op.inputs) == 1 output = output.op.inputs[0] return nn.sigmoid_cross_entropy_with_logits(labels=target, logits=output) # Compute cross entropy from probabilities. bce = target * math_ops.log(output + epsilon()) bce += (1 - target) * math_ops.log(1 - output + epsilon()) return -bce 

لكي أكون أمينًا ، أرفقت أدمغتي بهذه الأسطر القليلة من الشفرة لفترة طويلة جدًا. أولاً ، من الواضح على الفور أنه يمكن تنفيذ تطبيقين: إما سيتم استدعاء sigmoid_cross_entropy_with_logits ، أو ستعمل آخر مجموعة من الأسطر. الفرق هو أن sigmoid_cross_entropy_with_logits يعمل مع logits (كما يوحي الاسم ، doh) ، والرمز الرئيسي يعمل مع الاحتمالات.

من هم logits؟ إذا قرأت مليون مقالة مختلفة حول الموضوع ، فسوف يذكرون التعاريف الرياضية والصيغ وشيء آخر. في الممارسة العملية ، يبدو كل شيء بسيطًا بشكل مدهش (صححني إذا كنت مخطئًا). الناتج الخام للتنبؤ هو logits. حسنًا ، أو احتمالات اللوغاريتم ، فإن الاحتمالات اللوغاريتمية التي تُقاس بالسجل istic un its - الببغاوات اللوجستية.

 ln(1/2) == -0.69 ln(2/1) == 0.69 ln(1/100) == -4.6 ln(100/1) == 4.6 

في حالة tensorflow ، يعتبر هذا تعسفيًا إلى حد ما ، لأنه ، بالمعنى الدقيق للكلمة ، لا يكون إخراج الطبقة حسابيًا ، لكنه مقبول بالفعل. إذا كانت القيمة الخام من -∞ إلى + ∞ - فقم بتسجيل الدخول. ثم يمكن تحويلها إلى احتمالات. هناك خياران لهذا: softmax وحالته الخاصة ، السيني. Softmax - خذ متجهًا من logits ، وقم بتحويله إلى متجه من الاحتمالات ، وحتى يتضح أن مجموع احتمال كل الأحداث فيه هو 1. يأخذ Sigmoid (في حالة tf) أيضًا متجهًا من logits ، لكن يحول كل منهما إلى احتمالات منفصلة ، بشكل مستقل من الباقي.

 # 1+ln(0.5) == 0.30685281944 tf.math.softmax(tf.constant([0.30685281944, 1.0, 0.30685281944])) ## <tf.Tensor: shape=(3,), dtype=float32, numpy=array([0.25, 0.5 , 0.25], dtype=float32)> tf.math.sigmoid(tf.constant([0.30685281944, 1.0, 0.30685281944])) ## <tf.Tensor: shape=(3,), dtype=float32, numpy=array([0.57611686, 0.7310586 , 0.57611686], dtype=float32)> 

يمكنك أن تبحث في هذا الطريق. هناك مهام تصنيف متعدد التسمية ، وهناك مهام تصنيف متعدد الطبقات. Multiclass - هذا إذا كنت بحاجة إلى تحديد التفاح في الصورة أو البرتقال ، وربما حتى الأناناس. و multilabel هو عندما يمكن أن يكون هناك إناء فواكه في الصورة وعليك أن تقول أنه يحتوي على التفاح والبرتقال ، ولكن لا توجد أناناس. إذا كنا نريد multiclass - نحتاج softmax ، إذا كنا نريد multilabel - نحن بحاجة إلى السيني.
هنا لدينا حالة multilabel - من الضروري لكل بكسل (فئة) أن يقول ما إذا كان مثبتًا أم لا.

بالعودة إلى tensorflow ولماذا في crossentropy الثنائية (على الأقل في وظائف crossentropy الأخرى هو نفسه تقريبا) هناك فرعين عالميين. يعمل Crossentropy دائمًا مع الاحتمالات ، وسنتحدث عن ذلك لاحقًا. ثم هناك طريقتان: إما أن تدخل الاحتمالات بالفعل في الإدخال ، أو تأتي السجلات إلى المدخلات - ثم يتم تطبيق السينيويد عليها أولاً للحصول على الاحتمال. لقد حدث أن تطبيق السيني والحساب المتقاطع كان أفضل من مجرد حساب التداخل من الاحتمالات (مصدر الدالة sigmoid_cross_entropy_with_logits يحتوي على استنتاج رياضي ، بالإضافة إلى فضولي ، يمكنك google "الثبات العددي المتقاطع") وظائف crossentropy الإدخال ، وإرجاع logits الخام. حسنًا ، في الكود ، يتم التحقق من وظائف الخسارة إذا كانت الطبقة الأخيرة هي السيني ، ثم ستقوم بقطعها وتأخذ مدخلات التفعيل بدلاً من إخراجها للحساب ، وإرسال كل شيء ليتم مراعاتها في sigmoid_cross_entropy_with_logits .

حسنًا ، تم الفرز ، الآن binary_crossentropy. هناك تفسيران شائعان "حدسيان" يقيسان إنتروبيا.

أكثر رسمية: تخيل أن هناك نموذجًا معينًا يعرف بالنسبة لفئات n احتمال حدوثها (y ₀ ، y ₁ ، ... ، y _n ). والآن في الحياة ، نشأت كل فئة من هذه الفئات k _n مرة (k ₁ ، k ₁ ، ... ، k _n ). احتمال مثل هذا الحدث هو نتاج الاحتمال لكل فئة على حدة - (y ₁ ^ k ₁ ) (y ₂ ^ k ₂ ) ... (y _n ^ k _n ). من حيث المبدأ - هذا هو بالفعل تعريف طبيعي للانتروبيا - يتم التعبير عن احتمال مجموعة بيانات واحدة من حيث احتمال مجموعة بيانات أخرى. تكمن مشكلة هذا التعريف في أنه سيكون من 0 إلى 1 وغالبًا ما يكون صغيرًا جدًا ؛ وليس من المناسب مقارنة هذه القيم.
إذا أخذنا اللوغاريتم من هذا ، فسوف يخرج سجل k ₁ (y ₁ ) + k ₂ log (y ₂ ) وهكذا. يصبح نطاق القيم من -∞ إلى 0. اضرب كل هذا في -1 / n - ويظهر النطاق من 0 إلى +، ، علاوة على ذلك ، يتم التعبير عنها على أنها مجموع القيم لكل فئة ، وينعكس التغيير في كل فئة في القيمة الإجمالية بطريقة يمكن التنبؤ بها للغاية.

أكثر بساطة: يُظهر إنتروبيا عدد البتات الإضافية اللازمة للتعبير عن العينة من حيث النموذج الأصلي. إذا كنا هناك لعمل لوغاريتم مع القاعدة 2 ، فسنذهب بتات مباشرة. نحن نستخدم اللوغاريتمات الطبيعية في كل مكان ، لذلك تظهر عدد نات ( https://en.wikipedia.org/wiki/Nat_(unit )) ، وليس البتات.

الانتروبيا الثنائية ، بدورها ، هي حالة خاصة للإنتروبيا العادية ، عندما يكون عدد الطبقات اثنين. ثم لدينا معرفة كافية باحتمال حدوث فئة واحدة - y ₁ ، واحتمال حدوث الثانية ستكون (1-y ₁ ).

ولكن ، يبدو لي ، انزلقت لي قليلاً. واسمحوا لي أن أذكرك ، أنه في آخر مرة حاولنا فيها إنشاء أداة تشفير تلقائية للهوية ، أظهر لنا صورة جميلة ، وحتى دقة 1.0 ، ولكن في الواقع تبين أن الأرقام كانت فظيعة. من أجل التجربة ، يمكنك إجراء مزيد من الاختبارات:
1) يمكن إزالة التنشيط تماما ، سيكون هناك هوية نظيفة
2) يمكنك تجربة وظائف التنشيط الأخرى ، على سبيل المثال نفس relu

بدون تفعيل:

 model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, use_bias=False, kernel_initializer=tf.keras.initializers.Identity())) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1))) 

نحصل على نموذج الهوية المثالي:

 model.evaluate(x=val.map(lambda x: (x,x)).batch(BATCH_SIZE, drop_remainder=True)) # 8/Unknown - 1s 173ms/step - loss: 0.0000e+00 - accuracy: 1.0000[0.0, 1.0] 

التدريب ، بالمناسبة ، لن يؤدي إلى أي شيء ، لأن الخسارة == 0.0.

الآن مع relu. الرسم البياني الخاص به يشبه هذا:

 import matplotlib.ticker as plticker range_tensor = tf.range(-4, 4, 0.01, dtype=tf.float32) fig, ax = plt.subplots(1,1) plt.plot(range_tensor.numpy(), tf.keras.activations.relu(range_tensor).numpy()) ax.grid(which='major', linestyle='-', linewidth='0.5', color='red') ax.grid(which='minor', linestyle=':', linewidth='0.5', color='black') ax.yaxis.set_major_locator(plticker.MultipleLocator(base=1) ) plt.minorticks_on() 

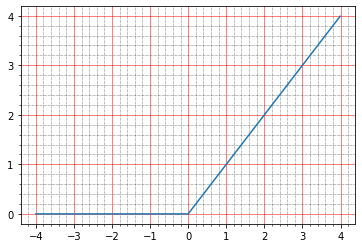
أقل من صفر - صفر ، أعلى - ص = س ، أي من الناحية النظرية ، يجب أن نحصل على نفس التأثير كما هو الحال في غياب التنشيط - نموذج مثالي.

 model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, activation='relu', use_bias=False, kernel_initializer=tf.keras.initializers.Identity())) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1))) model.compile(optimizer="adam", loss="binary_crossentropy", metrics=["accuracy"]) model.evaluate(x=val.map(lambda x: (x,x)).batch(BATCH_SIZE, drop_remainder=True)) # 8/Unknown - 1s 158ms/step - loss: 0.0000e+00 - accuracy: 1.0000[0.0, 1.0] 

حسنًا ، اكتشفنا نموذج الهوية ، حتى مع وجود جزء من النظرية أصبح أكثر وضوحًا. الآن دعونا نحاول تدريب نفس النموذج حتى يصبح هويته.

للمتعة ، سأجري هذه التجربة على ثلاث وظائف تنشيط. بادئ ذي بدء - relu ، لأنها أظهرت نفسها في وقت مبكر (كل شيء كما كان من قبل ، ولكن kernel_initializer تتم إزالته ، لذلك سيكون افتراضيًا glorot_uniform ):

 model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, activation='relu', use_bias=False)) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1))) 

يتعلم بشكل رائع:

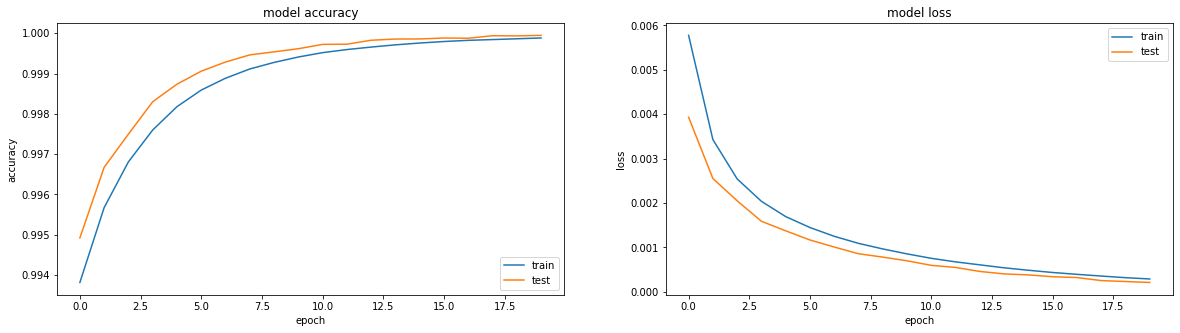
كانت النتيجة جيدة للغاية ، الدقة: 0.9999 ، الخسارة (mse): 2e-04 بعد 20 عصور ويمكنك التدريب أكثر.

بعد ذلك ، حاول باستخدام السيني:

 model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, activation='sigmoid', use_bias=False)) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1))) 

لقد قمت بالفعل بتدريس شيء مماثل من قبل ، مع وجود الفرق الوحيد في أن هذا التحيز معطل هنا. يدرس بجنون ويذهب على هضبة في المنطقة من العصر 50 ، دقة: 0.9970 ، خسارة: 0.01 بعد 60 عصور.

النتيجة مرة أخرى ليست مثيرة للإعجاب:

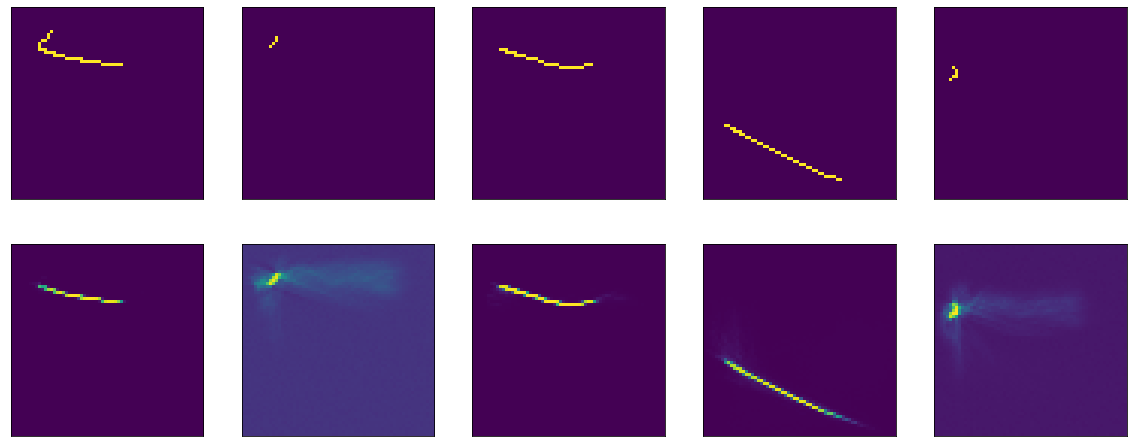
حسنا ، تحقق أيضا تانه:

 model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, activation='tanh', use_bias=False)) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1))) 

النتيجة قابلة للمقارنة مع relu - الدقة: 0.9999 ، الخسارة: 6e-04 بعد 20 عصور ، ويمكنك التدريب بشكل إضافي:

في الواقع ، أنا معذبة من مسألة ما إذا كان يمكن القيام بشيء ما لجعل السيني تظهر نتيجة مماثلة. حصرياً من الاهتمام الرياضي.

على سبيل المثال ، يمكنك محاولة إضافة BatchNormalization:

 model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, activation='sigmoid', use_bias=False)) model.add(tf.keras.layers.BatchNormalization()) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1))) 

ثم يحدث نوع من السحر. في العصر الثالث عشر ، الدقة: 1.0. والنتائج النارية:

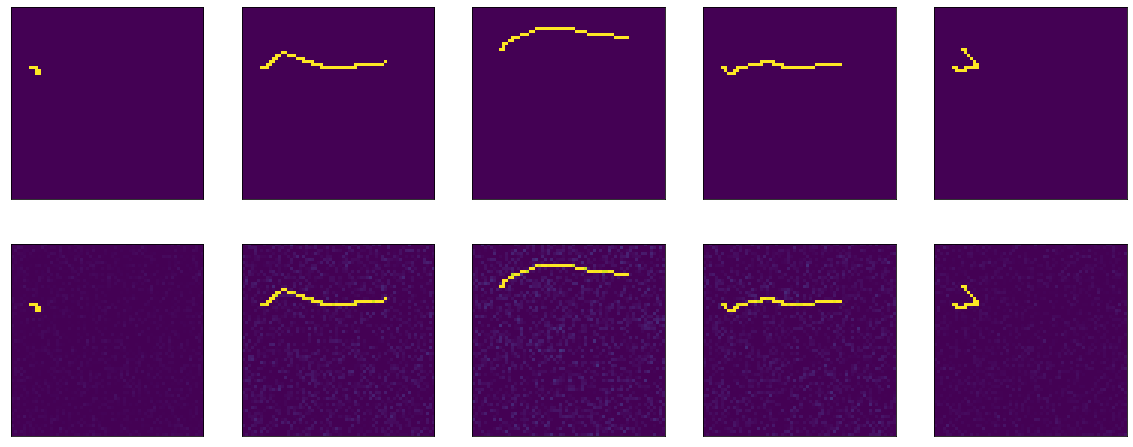
Iiiii ... على هذا الجرف المعلق ، سأنتهي من الجزء الأول ، لأن النص بالفعل dofig للغاية ، وليس من الواضح ما إذا كان شخص ما بحاجة إليه أم لا. في الجزء الثاني ، سوف أفهم ما حدث السحر ، وتجرب مع مُحسِّنين مختلفين ، وحاول بناء جهاز فك تشفير صادق ، وضرب رأسي على الطاولة. آمل أن يكون شخص ما مهتمًا ومفيدًا.