SVM. شرح من الصفر والتنفيذ في الثعبان. تحليل مفصل لطريقة ناقل الدعم

مرحبا لكل من اختار طريق ML-Samurai!

مقدمة:

في هذه المقالة ، نأخذ بعين الاعتبار طريقة آلة ناقلات الدعم ( Eng. SVM ، Support Vector Machine ) لمشكلة التصنيف. سيتم تقديم الفكرة الرئيسية للخوارزمية ، وسيتم تحليل ناتج تحديد الأوزان وتنفيذ DIY بسيط. على سبيل المثال من مجموعة البيانات $$$القزحي$ سيتم عرض تشغيل الخوارزمية المكتوبة مع البيانات المفصولة خطيًا / غير القابلة للفصل في الفضاء $$$R ^ 2$ والتصور من التدريب / التشخيص. بالإضافة إلى ذلك ، إيجابيات وسلبيات الخوارزمية ، سيتم الإعلان عن تعديلاتها.

الشكل 1. صورة مفتوحة المصدر من زهرة القزحية

المشكلة التي يتعين حلها:

سوف نقوم بحل مشكلة التصنيف الثنائي (عند وجود فئتين فقط). أولاً ، تدرب الخوارزمية على كائنات من مجموعة التدريب ، والتي تُعرف بها تصنيفات الفصل مسبقًا. علاوة على ذلك ، تتوقع الخوارزمية المدربة بالفعل تسمية الفصل لكل كائن من عينة الاختبار / المؤجلة. يمكن أن تسميات الفئة تأخذ القيم $$$Y = \ {- 1 ، +1 \}$ . كائن - ناقل مع علامات N $$$x = (x_1 ، x_2 ، ... ، x_n)$ في الفضاء $$$R ^ n$ . عند التعلم ، يجب أن تقوم الخوارزمية بإنشاء وظيفة $$$F (x) = y$ الذي يأخذ حجة $$$x$ - كائن من الفضاء $$$R ^ n$ ويعطي تسمية الفصل $$$ذ$ .

كلمات عامة حول الخوارزمية:

تتعلق مهمة التصنيف بالتدريس مع المعلم. SVM هي خوارزمية تعليمية مع المعلم. بصريا ، يمكن العثور على العديد من خوارزميات التعلم الآلي في هذا المقال من الدرجة الأولى (انظر قسم "خريطة عالم التعلم الآلي"). يجب إضافة أنه يمكن أيضًا استخدام SVM لمشاكل الانحدار ، ولكن سيتم تحليل مصنف SVM في هذه المقالة.

الهدف الرئيسي من SVM كمصنف هو إيجاد معادلة للطائرة الفاصلة الفاصلة
$$$w_1x_1 + w_2x_2 + ... + w_nx_n + w_0 = 0$ في الفضاء $$$R ^ n$ ، والتي من شأنها أن تقسم الفئتين في بعض الطريقة المثلى. منظر عام للتحول $$$F$ موضوع $$$x$ إلى فئة التسمية $$$Y$ : $$$F (x) = علامة (w ^ Tx-b)$ . سوف نتذكر أننا حددنا $$$w = (w_1 ، w_2 ، ... ، w_n) ، b = -w_0$ . بعد إعداد الأوزان الخوارزمية $$$w$ و $$$ب$ (التدريب) ، سيتم توقع كل الكائنات التي تقع على جانب واحد من الطائرة المفرطة التي تم إنشاؤها كفئة أولى ، والكائنات التي تقع على الجانب الآخر - الفئة الثانية.

وظيفة داخل $$ هناك مجموعة خطية من ميزات الكائن مع أوزان الخوارزمية ، وهذا هو السبب يشير SVM إلى الخوارزميات الخطية. يمكن إنشاء طائرة تشعبية مقسمة بطرق مختلفة ، ولكن بأوزان SVM $$$w$ و $$$ب$ تم تكوينها بحيث تكمن كائنات الفئة بعيدًا قدر الإمكان عن الطائرة الفاصلة الفاصلة. بمعنى آخر ، تعمل الخوارزمية على زيادة الفجوة ( الهامش الإنجليزي ) بين المستوى الفائق وبين كائنات الفئة الأقرب إليها. وتسمى هذه الأشياء ناقلات الدعم (انظر الشكل 2). ومن هنا جاء اسم الخوارزمية.

الشكل 2. SVM (أساس الشكل من هنا )

مخرجات مفصلة لقواعد ضبط مقياس SVM:

للحفاظ على المستوى الفائق للقسمة قدر الإمكان من نقاط العينة ، يجب أن يكون عرض الشريط كحد أقصى. سهم التوجيه $$$w$ هو ناقل الاتجاه من hyperplane تقسيم. فيما يلي ، نشير إلى المنتج القياسي لعدد من المتجهات كما $$$\ langle a، b \ rangle$ أو $$$a ^ Tb$ دعنا نجد إسقاط المتجه الذي ستكون نهايته متجهات الدعم لفئات مختلفة على متجه الاتجاه للطائرة المفرطة. سيوضح هذا الإسقاط عرض شريط التقسيم (انظر الشكل 3):

الشكل 3. مخرجات قواعد تحديد المقاييس (أساس الشكل من هنا )

هامش الكائن x من حدود الفئة هي القيمة $$$M = y (w ^ Tx-b)$ . تقوم الخوارزمية بخطأ في الكائن إذا وفقط إذا كانت المسافة البادئة $$$M$ سلبية (متى $$$ذ$ و $$$(w ^ Tx-b)$ شخصيات مختلفة). إذا $$$M ∈ (0 ، 1)$ ، ثم يقع الكائن داخل الشريط الفاصل. إذا $$$M> 1 دولا$ ، ثم يتم تصنيف الكائن x بشكل صحيح ، ويقع على مسافة ما من شريط التقسيم. نكتب هذا الاتصال:

النظام الناتج هو إعداد SVM الافتراضي مع SVM بهامش ثابت ، عندما لا يُسمح لأي كائن بالدخول إلى نطاق الفصل. يتم حلها بشكل تحليلي من خلال نظرية كون تاكر. المشكلة الناتجة تعادل المشكلة المزدوجة لإيجاد نقطة السرج لوظيفة Lagrange.

$$عرض $$ $ \ left \ {\ start {array} {ll} (w ^ Tw) / 2 \ rightarrow min & \ textrm {} \\ y (w ^ Tx-b) \ geqslant 1 & \ textrm {} \ end {array} \ right. عرض $$ $

كل هذا جيد طالما أن فصولنا قابلة للفصل بشكل خطي. حتى تتمكن الخوارزمية من العمل مع بيانات لا يمكن فصلها خطيًا ، دعنا نحول نظامنا قليلاً. دع الخوارزمية ترتكب أخطاء في الكائنات التدريبية ، ولكن في نفس الوقت حاول الاحتفاظ بأخطاء أقل. نقدم مجموعة من المتغيرات الإضافية $$$\ xi _i> 0$ تميز حجم الخطأ في كل كائن $$$x_i$ . نقدم عقوبة للخطأ الكلي في الحد الأدنى الوظيفي:

$$عرض $$ $ \ left \ {\ start {array} {ll} (w ^ Tw) / 2 + \ alpha \ sum \ xi _i \ rightarrow min & \ textrm {} \\ y (w ^ Tx_i-b) \ geqslant 1 - \ xi _i & \ textrm {} \\ \ xi _i \ geqslant0 & \ textrm {} \ end {array} \ right. عرض $$ $

سننظر في عدد أخطاء الخوارزمية (عندما يكون M <0). نسميها عقوبة . عندها تكون عقوبة كل الكائنات مساوية لمقدار الغرامات لكل كائن $$$x_i$ حيث $$$[M_i <0]$ - وظيفة العتبة (انظر الشكل 4):

$$عرض $$ $$ [M_i <0] = \ left \ {\ start {array} {ll} 1 & \ textrm {if} M_i <0 \\ 0 & \ textrm {if} M_i \ geqslant 0 \ end {صفيف} \ اليمين. عرض $$ $

بعد ذلك ، نجعل الجزاء حساسًا لحجم الخطأ وفي الوقت نفسه نقدم ركلة جزاء عند الاقتراب من الكائن إلى حدود الفصل:

عند إضافة إلى التعبير عقوبة عقوبة $$$\ alpha (w ^ Tw) / 2$ نحصل على وظيفة فقد SVM الكلاسيكية مع فجوة ناعمة ( SVM ذات هامش ضعيف ) لكائن واحد:

$$$ف دولا$ - وظيفة الخسارة ، بل هي أيضا وظيفة الخسارة. هذا هو ما سنقوم بتقليله بمساعدة النسب المتدرج في تنفيذ اليدين. نشتق قواعد تغيير الأوزان ، أين $$$\ eta$ - خطوة النسب:

$$عرض $$ $$ \ bigtriangledown Q = \ left \ {\ start {array} {ll} \ alpha w-yx & \ textrm {if} yw ^ Tx <1 \\ \ alpha w & \ textrm {if} yw ^ Tx \ geqslant 1 \ end {array} \ right. عرض $$ $

أسئلة محتملة في المقابلات (بناءً على أحداث حقيقية):

بعد الأسئلة العامة حول SVM: لماذا يزيد Hinge_loss من الخلوص؟ - أولاً ، تذكر أن الطائرة المفرطة تغير موقعها عندما تتغير الأوزان $$$w$ و $$$ب$ . تبدأ أوزان الخوارزمية في التغير عندما لا تتساوى تدرجات دالة الخسارة مع الصفر (عادةً ما يقولون: "التدرجات المتدفقة"). لذلك ، قمنا باختيار وظيفة الخسارة هذه خصيصًا ، حيث يبدأ التدرج في التدفق في الوقت المناسب. $$ يشبه هذا: $$$H = الحد الأقصى (0،1-y (w ^ Tx))$ . تذكر أن التخليص $$$m = y (w ^ Tx)$ . عندما الفجوة $$$م دولا$ كبيرة بما يكفي ( $$$1$ أو أكثر) التعبير $$$(1 م) دولا$ يصبح أقل من الصفر و $$$H = 0$ (لذلك ، لا تتدفق التدرجات ولا يتغير وزن الخوارزمية بأي طريقة). إذا كانت الفجوة m صغيرة بدرجة كافية (على سبيل المثال ، عندما يقع كائن في نطاق الفصل و / أو سالب (إذا كانت توقعات التصنيف غير صحيحة) ، يصبح Hinge_loss موجبًا ( $$$H> 0$ ) ، تبدأ التدرجات في التدفق وتتغير أوزان الخوارزمية. التلخيص: تتدفق التدرجات في حالتين: عندما يقع كائن العينة داخل نطاق الفصل وعند تصنيف الكائن بشكل غير صحيح.

للتحقق من مستوى اللغة الأجنبية ، هناك أسئلة مماثلة ممكنة: ما هي أوجه التشابه والاختلاف بين LogisticRegression و SVM؟ - أولاً ، سنتحدث عن أوجه التشابه: كلتا الخوارزميات خوارزميات تصنيف خطي في التعلم الخاضع للإشراف. بعض أوجه التشابه في حججهم من وظائف الخسارة: $$$log (1 + exp (-y (w ^ Tx)))$ ل logreg و $$$كحد أقصى (0،1 - ص (w ^ Tx))$ ل SVM (انظر الصورة 4). كل من الخوارزميات يمكننا تكوين باستخدام النسب التدرج. بعد ذلك ، دعونا نتحدث عن الاختلافات: يقوم SVM بإرجاع تسمية فئة الكائن على عكس LogReg ، والتي تُرجع احتمال عضوية الفئة. لا يمكن لـ SVM العمل مع تسميات الفصل الدراسي $$$\ {0،1 \}$ (بدون إعادة تسمية الفئات) بخلاف LogReg (خسارة خسارة LogReg لـ $$$\ {0،1 \}$ : $$$-ylog (p) - (1-y) log (1-p)$ اين $$$ذ$ - فئة حقيقية $$$ع$ - خوارزمية العودة ، احتمال الانتماء الكائن $$$x$ إلى الصف $$$\ {1 \}$ ). أكثر من ذلك ، يمكننا حل مشكلة SVM ذات الهامش الثابت دون هبوط متدرج. يتم تقليل مهمة البحث عن متجهات الدعم للبحث عن نقطة سرج في وظيفة Lagrange - تشير هذه المهمة إلى البرمجة التربيعية فقط.

import numpy as np import matplotlib.pyplot as plt %matplotlib inline xx = np.linspace(-4,3,100000) plt.plot(xx, [(x<0).astype(int) for x in xx], linewidth=2, label='1 if M<0, else 0') plt.plot(xx, [np.log2(1+2.76**(-x)) for x in xx], linewidth=4, label='logistic = log(1+e^-M)') plt.plot(xx, [np.max(np.array([0,1-x])) for x in xx], linewidth=4, label='hinge = max(0,1-M)') plt.title('Loss = F(Margin)') plt.grid() plt.legend(prop={'size': 14}); 

الشكل 4. وظائف الخسارة

تطبيق بسيط للهامش الناعم الكلاسيكي SVM:

تحذير! ستجد رابط للكود الكامل في نهاية المقال. أدناه هي كتل من التعليمات البرمجية التي أخرجت من السياق. لا يمكن أن تبدأ بعض الكتل إلا بعد التمرين على الكتل السابقة. تحت العديد من القطع ، سيتم وضع الصور التي توضح كيفية عمل الشفرة الموضوعة فوقه.

 import numpy as np import warnings warnings.filterwarnings('ignore') import matplotlib.pyplot as plt import matplotlib.lines as mlines plt.rcParams['figure.figsize'] = (8,6) %matplotlib inline from sklearn.datasets import load_iris from sklearn.decomposition import PCA from sklearn.model_selection import train_test_split def newline(p1, p2, color=None): #    #function kredits to: https://fooobar.com/questions/626491/how-to-draw-a-line-with-matplotlib ax = plt.gca() xmin, xmax = ax.get_xbound() if(p2[0] == p1[0]): xmin = xmax = p1[0] ymin, ymax = ax.get_ybound() else: ymax = p1[1]+(p2[1]-p1[1])/(p2[0]-p1[0])*(xmax-p1[0]) ymin = p1[1]+(p2[1]-p1[1])/(p2[0]-p1[0])*(xmin-p1[0]) l = mlines.Line2D([xmin,xmax], [ymin,ymax], color=color) ax.add_line(l) return l 

 def add_bias_feature(a): a_extended = np.zeros((a.shape[0],a.shape[1]+1)) a_extended[:,:-1] = a a_extended[:,-1] = int(1) return a_extended class CustomSVM(object): __class__ = "CustomSVM" __doc__ = """ This is an implementation of the SVM classification algorithm Note that it works only for binary classification ############################################################# ###################### PARAMETERS ###################### ############################################################# etha: float(default - 0.01) Learning rate, gradient step alpha: float, (default - 0.1) Regularization parameter in 0.5*alpha*||w||^2 epochs: int, (default - 200) Number of epochs of training ############################################################# ############################################################# ############################################################# """ def __init__(self, etha=0.01, alpha=0.1, epochs=200): self._epochs = epochs self._etha = etha self._alpha = alpha self._w = None self.history_w = [] self.train_errors = None self.val_errors = None self.train_loss = None self.val_loss = None def fit(self, X_train, Y_train, X_val, Y_val, verbose=False): #arrays: X; Y =-1,1 if len(set(Y_train)) != 2 or len(set(Y_val)) != 2: raise ValueError("Number of classes in Y is not equal 2!") X_train = add_bias_feature(X_train) X_val = add_bias_feature(X_val) self._w = np.random.normal(loc=0, scale=0.05, size=X_train.shape[1]) self.history_w.append(self._w) train_errors = [] val_errors = [] train_loss_epoch = [] val_loss_epoch = [] for epoch in range(self._epochs): tr_err = 0 val_err = 0 tr_loss = 0 val_loss = 0 for i,x in enumerate(X_train): margin = Y_train[i]*np.dot(self._w,X_train[i]) if margin >= 1: #   self._w = self._w - self._etha*self._alpha*self._w/self._epochs tr_loss += self.soft_margin_loss(X_train[i],Y_train[i]) else: #         0<m<1 self._w = self._w +\ self._etha*(Y_train[i]*X_train[i] - self._alpha*self._w/self._epochs) tr_err += 1 tr_loss += self.soft_margin_loss(X_train[i],Y_train[i]) self.history_w.append(self._w) for i,x in enumerate(X_val): val_loss += self.soft_margin_loss(X_val[i], Y_val[i]) val_err += (Y_val[i]*np.dot(self._w,X_val[i])<1).astype(int) if verbose: print('epoch {}. Errors={}. Mean Hinge_loss={}'\ .format(epoch,err,loss)) train_errors.append(tr_err) val_errors.append(val_err) train_loss_epoch.append(tr_loss) val_loss_epoch.append(val_loss) self.history_w = np.array(self.history_w) self.train_errors = np.array(train_errors) self.val_errors = np.array(val_errors) self.train_loss = np.array(train_loss_epoch) self.val_loss = np.array(val_loss_epoch) def predict(self, X:np.array) -> np.array: y_pred = [] X_extended = add_bias_feature(X) for i in range(len(X_extended)): y_pred.append(np.sign(np.dot(self._w,X_extended[i]))) return np.array(y_pred) def hinge_loss(self, x, y): return max(0,1 - y*np.dot(x, self._w)) def soft_margin_loss(self, x, y): return self.hinge_loss(x,y)+self._alpha*np.dot(self._w, self._w) 

نحن ندرس بالتفصيل تشغيل كل مجموعة من الخطوط:

1) قم بإنشاء دالة add_bias_feature (a) ، والتي تقوم تلقائيًا بتمديد متجه الكائنات ، وإضافة الرقم 1 إلى نهاية كل متجه ، وهذا ضروري من أجل "نسيان" المصطلح المجاني b. التعبير $$$w ^ Tx-b$ أي ما يعادل التعبير $$$w_1x_1 + w_2x_2 + ... + w_nx_n + w_0 * 1$ . نحن نفترض أن الوحدة هي العنصر الأخير من المتجه لجميع المتجهات x و $$$w_0 = -b$ . الآن تحديد الأوزان $$$w$ و $$$w_0 دولا$ سوف ننتج في نفس الوقت.

 def add_bias_feature(a): a_extended = np.zeros((a.shape[0],a.shape[1]+1)) a_extended[:,:-1] = a a_extended[:,-1] = int(1) return a_extended 

2) ثم سنصف المصنف نفسه. يحتوي على وظائف تهيئة init () ، وتعلم fit () ، والتنبؤ () ، وإيجاد فقدان الدالة hinge_loss () وإيجاد الخسارة الكلية لوظيفة الخوارزمية الكلاسيكية مع وجود فجوة ناعمة soft_margin_loss () .

3) عند التهيئة ، يتم تقديم 3 معلمات كبيرة: _etha - خطوة من أصل التدرج ( $$$\ eta$ ) ، _alpha - معامل سرعة تخفيض الوزن النسبي (قبل المصطلح التربيعي في دالة الخسارة $$$\ alpha$ ) ، _epochs - عدد عصور التدريب.

  def __init__(self, etha=0.01, alpha=0.1, epochs=200): self._epochs = epochs self._etha = etha self._alpha = alpha self._w = None self.history_w = [] self.train_errors = None self.val_errors = None self.train_loss = None self.val_loss = None 

4) أثناء التدريب لكل حقبة من عينة التدريب (X_train ، Y_train) ، سنأخذ عنصرًا واحدًا من العينة ، ونحسب الفجوة بين هذا العنصر وموضع الطائرة الفائقة في وقت معين. علاوة على ذلك ، بناءً على حجم هذه الفجوة ، سنقوم بتغيير وزن الخوارزمية باستخدام التدرج اللوني لوظيفة الخسارة $$$ف دولا$ . في نفس الوقت ، سنقوم بحساب قيمة هذه الوظيفة لكل فترة وعدد المرات التي نغير فيها الأوزان لكل فترة. قبل البدء في التدريب ، سوف نتأكد من أن ما لا يزيد عن تسميتين مختلفتين من الصفوف قد دخلوا فعلاً في وظيفة التعلم. قبل إعداد الرصيد ، تتم تهيئته باستخدام التوزيع الطبيعي.

  def fit(self, X_train, Y_train, X_val, Y_val, verbose=False): #arrays: X; Y =-1,1 if len(set(Y_train)) != 2 or len(set(Y_val)) != 2: raise ValueError("Number of classes in Y is not equal 2!") X_train = add_bias_feature(X_train) X_val = add_bias_feature(X_val) self._w = np.random.normal(loc=0, scale=0.05, size=X_train.shape[1]) self.history_w.append(self._w) train_errors = [] val_errors = [] train_loss_epoch = [] val_loss_epoch = [] for epoch in range(self._epochs): tr_err = 0 val_err = 0 tr_loss = 0 val_loss = 0 for i,x in enumerate(X_train): margin = Y_train[i]*np.dot(self._w,X_train[i]) if margin >= 1: #   self._w = self._w - self._etha*self._alpha*self._w/self._epochs tr_loss += self.soft_margin_loss(X_train[i],Y_train[i]) else: #         0<m<1 self._w = self._w +\ self._etha*(Y_train[i]*X_train[i] - self._alpha*self._w/self._epochs) tr_err += 1 tr_loss += self.soft_margin_loss(X_train[i],Y_train[i]) self.history_w.append(self._w) for i,x in enumerate(X_val): val_loss += self.soft_margin_loss(X_val[i], Y_val[i]) val_err += (Y_val[i]*np.dot(self._w,X_val[i])<1).astype(int) if verbose: print('epoch {}. Errors={}. Mean Hinge_loss={}'\ .format(epoch,err,loss)) train_errors.append(tr_err) val_errors.append(val_err) train_loss_epoch.append(tr_loss) val_loss_epoch.append(val_loss) self.history_w = np.array(self.history_w) self.train_errors = np.array(train_errors) self.val_errors = np.array(val_errors) self.train_loss = np.array(train_loss_epoch) self.val_loss = np.array(val_loss_epoch) 

التحقق من تشغيل الخوارزمية المكتوبة:

تحقق من أن الخوارزمية المكتوبة تعمل على نوع من مجموعة بيانات اللعبة. خذ مجموعة بيانات Iris. سنقوم بإعداد البيانات. دلالة الفصول 1 و 2 كما $$$+ 1 دولا$ ، والفئة 0 مثل $$$-1 دولا$ . باستخدام خوارزمية PCA (الشرح والتطبيق هنا ) ، نقوم على نحو أمثل بتقليل مساحة 4 سمات إلى 2 مع الحد الأدنى من فقدان البيانات (سيكون من السهل علينا مراقبة التدريب والنتيجة). بعد ذلك ، سنقسم إلى عينة تدريب (تدريب) وعينة متأخرة (التحقق من الصحة). سوف نقوم بالتدريب على عينة التدريب ، والتنبؤ والتحقق من المؤجلة. نختار عوامل التعلم بحيث تنخفض وظيفة الخسارة. أثناء التدريب ، سننظر في وظيفة الخسارة في التدريب وتأخر أخذ العينات.

 #    iris = load_iris() X = iris.data Y = iris.target pca = PCA(n_components=2) X = pca.fit_transform(X) Y = (Y > 0).astype(int)*2-1 # [0,1,2] --> [False,True,True] --> [0,1,1] --> [0,2,2] --> [-1,1,1] X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.4, random_state=2020) 

 #     svm = CustomSVM(etha=0.005, alpha=0.006, epochs=150) svm.fit(X_train, Y_train, X_test, Y_test) print(svm.train_errors) # numbers of error in each epoch print(svm._w) # w0*x_i[0]+w1*x_i[1]+w2=0 plt.plot(svm.train_loss, linewidth=2, label='train_loss') plt.plot(svm.val_loss, linewidth=2, label='test_loss') plt.grid() plt.legend(prop={'size': 15}) plt.show() 

 d = {-1:'green', 1:'red'} plt.scatter(X_train[:,0], X_train[:,1], c=[d[y] for y in Y_train]) newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') #  w0*x_i[0]+w1*x_i[1]+w2*1=0  #  x_i[0]=0, x_i[1]=0 newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1 newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 plt.show() 

 #    y_pred = svm.predict(X_test) y_pred[y_pred != Y_test] = -100 # find and mark classification error print('    : ', (y_pred == -100).astype(int).sum()) d1 = {-1:'lime', 1:'m', -100: 'black'} # black = classification error plt.scatter(X_test[:,0], X_test[:,1], c=[d1[y] for y in y_pred]) newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1 newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 plt.show() 

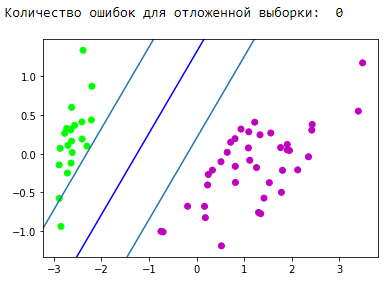
! ممتاز خوارزمية لدينا معالجة البيانات القابلة للفصل خطيا. الآن اجعلها منفصلة الفصلين 0 و 1 من الفصل 2:

 #    iris = load_iris() X = iris.data Y = iris.target pca = PCA(n_components=2) X = pca.fit_transform(X) Y = (Y == 2).astype(int)*2-1 # [0,1,2] --> [False,False,True] --> [0,1,1] --> [0,0,2] --> [-1,1,1] X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.4, random_state=2020) 

 #     svm = CustomSVM(etha=0.03, alpha=0.0001, epochs=300) svm.fit(X_train, Y_train, X_test, Y_test) print(svm.train_errors[:150]) # numbers of error in each epoch print(svm._w) # w0*x_i[0]+w1*x_i[1]+w2=0 plt.plot(svm.train_loss, linewidth=2, label='train_loss') plt.plot(svm.val_loss, linewidth=2, label='test_loss') plt.grid() plt.legend(prop={'size': 15}) plt.show() 

 d = {-1:'green', 1:'red'} plt.scatter(X_train[:,0], X_train[:,1], c=[d[y] for y in Y_train]) newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') #  w0*x_i[0]+w1*x_i[1]+w2*1=0  #  x_i[0]=0, x_i[1]=0 newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1 newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 plt.show() 

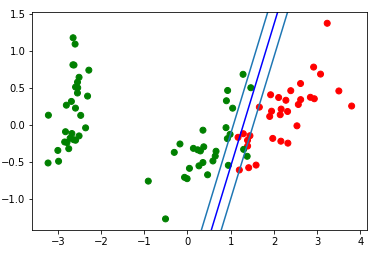
دعونا نلقي نظرة على gif ، التي ستوضح كيف غير خط التقسيم تغيير موقعه أثناء التدريب (فقط 500 إطار لتغيير الأوزان. أول 300 على التوالي. 200 قطعة التالية لكل إطار 130):

 import matplotlib.animation as animation from matplotlib.animation import PillowWriter def one_image(w, X, Y): axes = plt.gca() axes.set_xlim([-4,4]) axes.set_ylim([-1.5,1.5]) d1 = {-1:'green', 1:'red'} im = plt.scatter(X[:,0], X[:,1], c=[d1[y] for y in Y]) im = newline([0,-w[2]/w[1]],[-w[2]/w[0],0], 'blue') # im = newline([0,1/w[1]-w[2]/w[1]],[1/w[0]-w[2]/w[0],0], 'lime') #w0*x_i[0]+w1*x_i[1]+w2*1=1 # im = newline([0,-1/w[1]-w[2]/w[1]],[-1/w[0]-w[2]/w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 return im fig = plt.figure() ims = [] for i in range(500): if i<=300: k = i else: k = (i-298)*130 im = one_image(svm.history_w[k], X_train, Y_train) ims.append([im]) ani = animation.ArtistAnimation(fig, ims, interval=20, blit=True, repeat_delay=500) writer = PillowWriter(fps=20) ani.save("my_demo.gif", writer='imagemagick') 

 #    y_pred = svm.predict(X_test) y_pred[y_pred != Y_test] = -100 # find and mark classification error print('    : ', (y_pred == -100).astype(int).sum()) d1 = {-1:'lime', 1:'m', -100: 'black'} # black = classification error plt.scatter(X_test[:,0], X_test[:,1], c=[d1[y] for y in y_pred]) newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1 newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 plt.show() 

استقامة المساحات

من المهم أن نفهم أنه في المشكلات الحقيقية لن تكون هناك حالة بسيطة تحتوي على بيانات قابلة للفصل خطيًا. للعمل مع هذه البيانات ، تم اقتراح فكرة الانتقال إلى مساحة أخرى ، حيث سيتم فصل البيانات خطيًا. وتسمى هذه المساحة تصحيح. لن تتأثر تصحيح المسافات والنواة في هذه المقالة. يمكنك العثور على النظرية الرياضية الأكثر اكتمالا في ملخص 141516 من E. Sokolov وفي محاضرات K.V. Vorontsov .

باستخدام SVM من sklearn:

في الواقع ، تتم كتابة جميع خوارزميات تعلم الآلة الكلاسيكية تقريبًا. دعنا نعطي مثالاً على الكود ، سنأخذ الخوارزمية من مكتبة sklearn .

 from sklearn import svm from sklearn.metrics import recall_score C = 1.0 # = self._alpha in our algorithm model1 = svm.SVC(kernel='linear', C=C) #model1 = svm.LinearSVC(C=C, max_iter=10000) #model1 = svm.SVC(kernel='rbf', gamma=0.7, C=C) #model1 = svm.SVC(kernel='poly', degree=3, gamma='auto', C=C) model1.fit(X_train, Y_train) y_predict = model1.predict(X_test) print(recall_score(Y_test, y_predict, average=None)) 

إيجابيات وسلبيات SVM الكلاسيكية:

الايجابيات:

1. يعمل بشكل جيد مع مساحة ميزة كبيرة.
2. يعمل بشكل جيد مع البيانات الصغيرة ؛
3. لذلك تجد الخوارزمية الحد الأقصى لنطاق التقسيم ، والذي ، مثل الوسادة الهوائية ، يمكن أن يقلل من عدد أخطاء التصنيف ؛
4. نظرًا لأن الخوارزمية تنخفض إلى حل مشكلة البرمجة التربيعية في مجال محدب ، فإن هذه المشكلة لها دائمًا حل فريد (تكون الطائرة الفاصلة الفاصلة مع بعض المقاييس الفوقية للخوارزمية هي نفسها دائمًا).

سلبيات:

1. وقت تدريب طويل (لمجموعات البيانات الكبيرة) ؛
2. عدم ثبات الضوضاء: تصبح القيم المتطرفة في بيانات التدريب كائنات دخيلة مرجعية وتؤثر بشكل مباشر على بناء طائرة مفرطة منفصلة ؛
3. لم يتم شرح الطرق العامة لبناء النواة وتصحيح المسافات الأكثر ملاءمة لمشكلة معينة في حالة الفصل الخطي للفصل. اختيار تحويلات البيانات المفيدة هو الفن.

تطبيق SVM:

يعتمد اختيار خوارزمية تعلم الآلة أو آخر بشكل مباشر على المعلومات التي يتم الحصول عليها أثناء استخراج البيانات. ولكن بعبارات عامة ، يمكن تمييز المهام التالية:

• المهام مع مجموعة البيانات الصغيرة.
• مهام تصنيف النص. يوفر SVM خط أساس جيدًا ([المعالجة المسبقة] + [TF-iDF] + [SVM]) ، ودقة التنبؤ الناتجة على مستوى بعض الشبكات العصبية التلافيفية / المتكررة (أوصي بتجربة هذه الطريقة بنفسك لدمج المادة). ويرد مثال ممتاز هنا ، "الجزء 3. مثال على واحدة من الحيل التي نعلمها" ؛
• بالنسبة للعديد من المهام التي تحتوي على بيانات منظمة ، يكون الرابط [هندسة الميزات] + [SVM] + [kernel] "كعكة ثابتة"
• نظرًا لأن فقدان المفصلة يعتبر سريعًا جدًا ، يمكن العثور عليه في Vowpal Wabbit (افتراضيًا).

تعديلات الخوارزمية:

هناك العديد من الإضافات والتعديلات على طريقة متجه الدعم ، والتي تهدف إلى القضاء على بعض العيوب:

• جهاز ناقل الصلة (RVM)
• SVM أحادي القاعدة (LASSO SVM)
• نظام مزدوج SVM (FlexNet SVM)
• آلة ميزات الدعم (SFM)
• آلة ميزات الملاءمة (RFM)

مصادر إضافية على SVM:

1. محاضرات النص K.V. فورنتسوف
2. ملخصات E. Sokolov - 14.15.16
3. مصدر بارد من قبل ألكسندر كوالتشيك
4. على habr هناك 2 المقالات المكرسة ل svm:
   
   • 2010 العام
   • 2018 سنة
5. على github ، يمكنني تسليط الضوء على 2 تطبيقات SVM باردة على الروابط التالية:
   
   • خوارزميات من مطور محلي
   • ML-من-الصفر

الاستنتاج:

شكرا جزيلا لاهتمامكم! سأكون ممتنا لأية تعليقات ، وردود الفعل والنصائح.
ستجد الرمز الكامل من هذه المقالة على جيثب .

شكرا yorko للحصول على نصائح حول تجانس زوايا. بفضل أليكسي Sizykh - قسم الفيزياء والتكنولوجيا الذي استثمر جزئيا في الكود.