مساء الخير
كما وعدت في مقالي الأول ، أريد أن أطلعكم على إحدى طرق حل نظام معادلات ديوفانتاين. الغرض من هذا المقال هو تعريف القراء الآخرين بهذه التقنية ونقلها بطريقة أو بأخرى غير مفهومة.
النظر في نظام اثنين من المعادلات ديوفانتاين
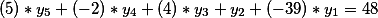
و

نجد كل الحلول الممكنة للمعادلة الأولى. كيف تسأل؟ بالتأكيد هناك طرق مختلفة ، لكنني سأشارك في إحدى المقالات التالية كيف يمكنني حل مشكلة مماثلة. الآن ، نحن نفترض فقط أن الحل العام لديه الشكل

كيف أتحقق من أنني لا أكذب؟
يكفي أن نتذكر حساب التفاضل والتكامل المصفوفة ومضاعفة متجه قيم معادلة ديوفانتاين الأولى (بدون مصطلح مجاني) بمصفوفة جميع المعاملات .

تم الحصول عليها نتيجة لقيمة المصطلح الحر ، وبالتالي الحسابات صحيحة
والخطوة التالية هي استبدال حلنا المشترك.

في المعادلة الثانية

الإجراء هو نفسه: نقوم بضرب المتجه من معاملات المعادلة الثانية بالمحلول العام الأول
نحصل على هذه النتيجة
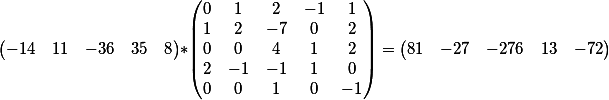
وهذا هو ، حصلنا على معادلة النموذج
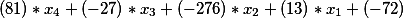
على الجانب الأيمن من معادلة ديوفانتاين الثانية ، حيث كان هناك مصطلح حر يساوي -335 ، بقي ، وهذا هو ، لدينا الحل النهائي في هذه المرحلة لديه شكل
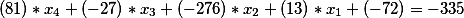
أو نقل الأعضاء الأحرار إلى اليمين الذي نحصل عليه
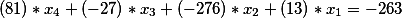
لذلك ، حصلنا على معادلة ديوفانتين القادمة. دعونا نجد الحل العام ونختبره من أجل الحقيقة.

وهذا هو ، والحل العام هو
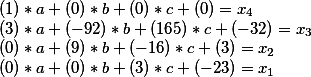
ونحن الآن نقوم بالتحويل العكسي (فليكن يسمى ذلك). هذا هو ، النظام

بدلاً من المجهول x نستبدل ما حدث في المرحلة الأخيرة
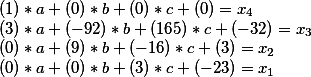
في حساب المصفوفات ، يتم حل هذا بضرب مصفوفة واحدة بأخرى.
ولكن مع المصفوفة الأولى ، يلزم إجراء معين: قم بإزالة (مؤقتًا) العمود الأخير بشروط حرة ، لأن هذه المعلمة لا تشارك في الضرب ، وسيتم استخدامها لاحقًا.
نتيجة ضرب اثنين من المصفوفات يولد
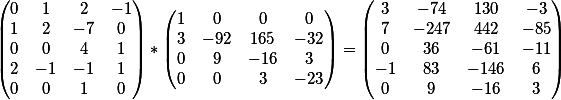
المصفوفة
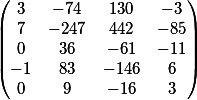
العمود الأخير هو الأعضاء الأحرار في هذا النظام.
نأخذ بعين الاعتبار العمود الذي تم حذفه مؤقتًا قبل الضرب وإضافته
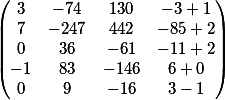
جوابنا النهائي في شكل مصفوفة
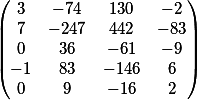
التحقق من ذلك؟
المنتج المتجه لمعاملات المعادلة الأولى والمصفوفة
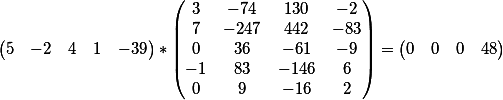
والمنتج المتجه لمعاملات المعادلة الثانية والمصفوفة
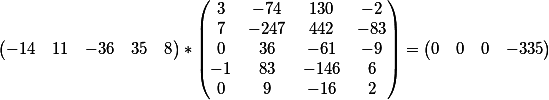
كما ترون ، تتزامن النتيجة مع التعبير الحر لكل من المعادلات.
وبالتالي ، فإن الحل العام لديه الشكل
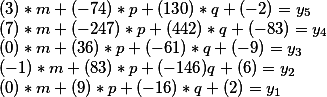
حيث m، p، q - يمكن أن تأخذ أي قيم عدد صحيح
بهذه الطريقة المباشرة ، يمكن حل معادلات ديوفانتا الخطية الأكثر تعقيدًا. تم إنشاء آلة حاسبة حقيقية في أعقاب هذه الخوارزمية ؛ هذه الآلة الحاسبة لا تحب حقًا عندما تحدث الأصفار بدلاً من القيم في معاملات المعادلة الأولى من النظام الأولي. ولكن هذه مشكلة في تطبيقي المحدد لهذه الخوارزمية.
في الموضوع التالي ، سوف أخبرك بكيفية إنشاء معادلات ديوفانتين باستخدام مصفوفة الحل العام. المهمة عمومًا عادية ويتم تنفيذها في عمل واحد ، ولكن فجأة لا يعرف أحد ما.
سأكون ممتنا للتعليقات والملاحظات والاقتراحات.