لعدة قرون ، بحث الباحثون عن أمثلة للحالات التي تثبت فيها معادلات أويلر للديناميكا المائية للسائل المثالي أنها غير صحيحة. وأخيرا ، وجد علماء الرياضيات مثالا على ذلك.
لسنوات عديدة ، يشك علماء الرياضيات في أن
معادلات أويلر سترفض العمل
في ظروف معينة. ومع ذلك ، لم يتمكنوا من وصف السيناريو المحدد الذي يحدث فيه هذا. حتى اليوم.
هذه المعادلات هي وصف رياضي مثالي لحركة السوائل. ضمن بعض الافتراضات ، يقومون بنمذجة انتشار الأمواج على البركة أو تسلل دبس السكر من العلبة. يجب أن يكونوا قادرين على وصف حركة أي سائل في أي ظرف من الظروف - ولأكثر من قرنين ، كان كذلك.
ومع ذلك ، فإن الأدلة الجديدة توضح أنه في ظل ظروف معينة ، لا تزال هذه المعادلات ترفض العمل.
قال
طارق الجندي ، عالم الرياضيات من جامعة كاليفورنيا في سان دييغو ، مؤلف كتاب جديد: "منذ عام ونصف ، أود أن أقول أنني لم أتوقع رؤية مثل هذا التطور حتى خلال حياتي".
أثبت الجندي وجود عيوب في معادلات أويلر في عملين تم نشرهما في عام 2019 - كتب
أبريل نفسه ،
وأكتوبر - بالتعاون مع
تج الدين جول ونادر مسمودي . انقلب العمل على مدى قرن من الافتراضات حول هذه المعادلات الشهيرة للسوائل.
قال
بيتر قسطنطين ، عالم الرياضيات في جامعة برينستون: "أعتقد أن هذا إنجاز رائع ورائع".
لا يعمل عمل الجندي في نهاية معادلات أويلر. إنه يثبت أنه في ظل ظروف معينة تمامًا ، تبدو المعادلات في ارتفاع درجة الحرارة وتبدأ في التخلي عن الهراء. ولكن في ظروف أكثر واقعية ، تظل المعادلات حتى الآن معرضة للخطر.
ومع ذلك ، فإن الاستثناء الذي وجده الجندي فاجأ علماء الرياضيات ، لأنه يحدث في ظل ظروف ، كما كان يعتقد سابقًا ، يجب أن تعمل المعادلة على أي حال.
وقال
فلاد فيكول ، عالم الرياضيات في جامعة نيويورك: "بشكل عام ، يبدو لي أن الناس فوجئوا بالمثال الذي قدمه طارق".
كيف هرع معادلات أويلر
اشتق
ليونارد يولر معادلات السوائل التي تحمل اسمه الآن في عام 1757. يصفون تطور السائل مع مرور الوقت ، تماماً كما تصف معادلات نيوتن حركة كرة البلياردو على الطاولة.
بتعبير أدق ، تشير هذه المعادلات إلى الحركة الآنية للجزيئات اللانهائية للسائل. يتضمن وصفهم سرعة الجسيم (السرعة والاتجاه الذي يتحرك فيه) وهذه الكمية المرتبطة به مثل
الدوامة (مدى سرعة دوران الجسيم بطريقة أعلى ، وفي أي اتجاه).
كل هذه المعلومات تشكل "حقل سرعة" بالكامل ، لقطة لحركة السوائل في وقت معين. تبدأ معادلات أويلر بحقل السرعة الأولي ، وتتوقع كيف سيتغير في أي وقت في المستقبل.
طارق الجنديلا تصف معادلات أويلر مائع العالم الحقيقي حرفيًا. وتشمل هذه العديد من الافتراضات غير المادية. على سبيل المثال ، لا تعمل إلا إذا كانت التدفقات الداخلية في السائل لا تسبب احتكاكًا ، وتتحرك نسبة إلى بعضها البعض. يُفترض أيضًا عدم قدرة السوائل ، وفقًا لقواعد معادلات أويلر ، من المستحيل ضغط سائل ، بوضعه في مساحة بحجم أصغر مما يتطلبه الأمر بالفعل.
كتب
فلاديمير سفيراك من جامعة مينيسوتا إلينا عبر البريد الإلكتروني: "يمكن تخيل هذا النموذج
كعالم مثالي ، ومعادلات كقواعد لحركة هذا العالم".
سمحت هذه الظروف غير العادية لعالم الرياضيات والفيزيائي جون فون نيومان بأن يقول مازحا إن هذه المعادلات تحاكي سلوك "الماء الجاف". لمحاكاة سائل أكثر واقعية يواجه الاحتكاك الداخلي (ما يسمى اللزوجة) ، يستخدم الباحثون
معادلات Navier-Stokes .
"معادلات أويلر مثالية للغاية. وقال كونستانتين: الاحتكاك موجود في سوائل حقيقية.
ولكن في الوقت نفسه ، لا تزال معادلات أويلر تحتل مكانة محترمة في العلوم. يود الباحثون معرفة ما إذا كانت هذه المعادلات تعمل بشكل واضح في إطار هذا العالم المثالي دون احتكاك وانضغاط - أي ما إذا كان يمكنهم وصف جميع الحالات المستقبلية لجميع الإصدارات الأولية الممكنة من حقول السرعة. أو بعبارة أخرى: هل هناك حركة سائلة لا يمكن لهذه المعادلات أن تصممها؟
"في جوهرها ، فإن السؤال بسيط: هل هذه المعادلات تؤدي دائما وظيفتها؟" قال سعيد سفراك.
من الناحية النظرية ، باستبدال قيم الحالة الحالية للسائل في المعادلات ، ستحصل على القيم الدقيقة لوصف حالتها المستقبلية. ثم يمكنك استبدال هذه القيم الجديدة مرة أخرى في المعادلات ، وتوسيع توقعاتك. وعادة ما يمكن مواصلة عملية مماثلة لأي مدة زمنية في المستقبل.
ومع ذلك ، فمن الممكن أيضًا في ظل ظروف نادرة جدًا كسر المعادلات. يمكنهم أن يصرخوا وينفخوا وينتجوا قيم إخراج مناسبة لدور معلمات الإدخال المستقبلية ، ثم ينتجون فجأة قيمة غير مناسبة لهم على الإطلاق. في مثل هذه الحالات ، يقول علماء الرياضيات أن المعادلات "هرع".
إذا اندفعت معادلات أويلر ، فسيكون السبب في ذلك أنها تبدأ في زيادة سرعة أو دوامة النقطة بطريقة غير طبيعية. سيكون هذا الكسب قويًا لدرجة أنه في وقت محدد تصبح سرعة أو دوامة نقطة ما غير نهائية. وبمجرد أن تعطي المعادلات قيمة لا حصر لها ، سوف تنهار وتتوقف عن وصف أي ظروف بيئية في المستقبل. هذا لأنه عادة ما يكون من المستحيل إجراء العمليات الحسابية ذات القيم اللانهائية - وهذا هو نفس القسمة على صفر (بالمناسبة ، قيم السرعة في هذه الحالة ستتجاوز سرعة الضوء - على الرغم من أنه في العالم المثالي للنموذج ، هذا ليس هو الأسوأ).
وتسمى هذه المعاني اللانهائية المشؤومة "التفردات". عندما يسأل علماء الرياضيات ، "هل تعمل معادلات أويلر دائمًا؟" ، يسألون في الواقع "هل هناك سيناريوهات تعطي فيها معادلات أويلر المفردات؟"
يعتقد الكثير من علماء الرياضيات أنه - حتى الآن ، لم يتمكنوا من العثور على سيناريو محدد تنفجر فيه المعادلات بالفعل.
وقال كونستانتين: "كان هناك شعور بأن يولر كان يحاول تجنب التفرد ، وحتى وقت قريب ، نجح".
لا يوضح العمل الجديد كيف تعطي المعادلات المفردات في ظل الظروف التي يهتم بها علماء الرياضيات. ومع ذلك ، فقد جاءت هذه النتيجة حتى الآن أقرب إلى الهدف من البقية. ولهذا ، اعتبر الجندي نموذجًا مبسطًا لحركة السوائل.
الحد من التعقيد
لدى علماء الرياضيات العديد من الطرق المختلفة لتقليل تعقيد حركة السوائل ، والتي يستخدمون فيها معادلات أويلر. تشتمل العديد من النتائج الأكثر إثارة للاهتمام ، على غرار تلك التي حققتها Elgindi ، على عرض يوضح مقدار ما يمكنك تبسيط سلوك المائع - أي ، إلى أي مدى يمكنك تبسيط البيانات التي يتم استبدالها في المعادلات - مع الاستمرار في القدرة على قول شيء ذي معنى حول المعادلات نفسها.
في سائل ثلاثي الأبعاد حقيقي ، مثل الماء في البركة ، يكون لأي جسيم ثلاثة محاور محتملة للحركة: المحور السيني (اليسار إلى اليمين) ، المحور ص (أعلى إلى أسفل) ، المحور z (إلى الأمام للخلف). الكثير من حرية الحركة. علاوة على ذلك ، فإن حركة الجزيئات في جزء واحد من السائل لن تكون بالضرورة مرتبطة بقوة بحركة الجزيئات في جزء آخر.
قال الجندي: "عليك أن تتبع الكثير".
في الورقة الجديدة ، يبسط Elgindi العمل لمعادلات Euler. يتطلب أن يكون السائل متماثلًا على طول المحور z ، والذي لا يوجد عادة في السوائل الحقيقية. بسبب التماثل ، يصبح من الأسهل حساب مجال السرعة ، لأنه من المعروف أن النقاط على جانبي المحور z متماثلتان مرآة. لذلك ، إذا كنت تعرف سرعة أو دوامة نقطة واحدة ، فأنت تحتاج فقط إلى تغيير علامة هذه القيم ، والحصول على هذه القيم لنقطة أخرى.
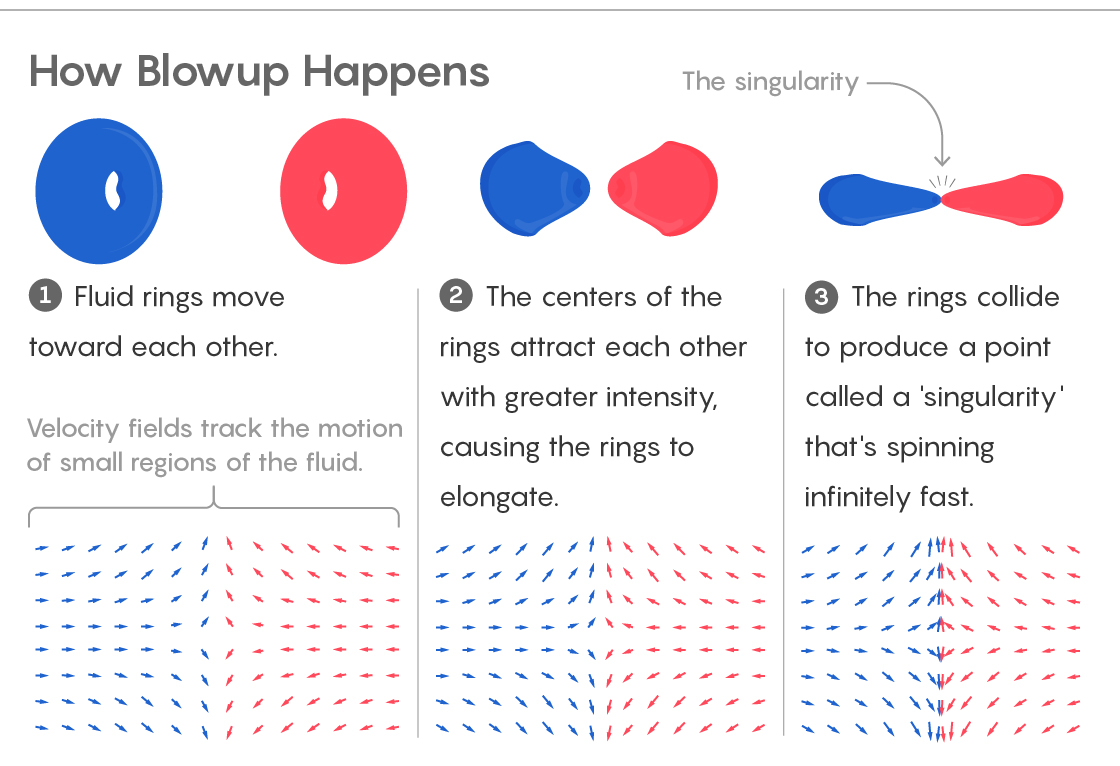1) السوائل تتحرك نحو. حقول السرعة تتبع حركة أقسام صغيرة من السوائل.
2) تنجذب مراكز الخواتم ، مما يؤدي إلى امتداد الخواتم.
3) تصطدم الخواتم ، مما يخلق نقطة من "التفرد" ، تدور بسرعة لا نهائية.كما أنه يحد من الحركة المحتملة للنقاط في السائل. يمكن نقل الجسيمات إما على طول المحور z ، أو بعيدًا عنها ، أو تجاهها. لا يمكنهم الدوران حول المحور z. يقول علماء الرياضيات إنه لا توجد دوامات في هذه السوائل.
"هذا يقلل المهمة إلى ثنائي الأبعاد" ، قال الجندي.
أخيرًا ، يفرض الجندي بعض الشروط على البيانات الأولية المقدمة في معادلات أويلر. بمعنى ما ، هذه البيانات أكثر صرامة من تلك التي تصف السوائل الحقيقية ، وتزيد من احتمال تكوين المفردات.
في الحياة الواقعية ، إذا انتقلت من نقطة إلى أخرى ، وتقع بالقرب منها ، فإن سرعات هاتين النقطتين ستكون متساوية تقريبًا. يجب أن تكون دوامات هاتين النقطتين متشابهة جدًا. يقول علماء الرياضيات إن حقول السرعة بهذه الخاصية "سلسة" ، أي أن القيم عليها تتغير تدريجياً - أو بسلاسة - عند الانتقال من نقطة إلى أخرى. لا تغييرات سريعة.
ولكن في حالة وصف السائل من الجندي ، كل شيء مختلف.
وقال فيكول: "يمكن أن يتغير تطور بيانات طارق كثيرًا". "يمكن أن تحتوي النقاط القريبة على دوامات مختلفة جدًا."
قد يبدو أن تبسيط الجندي بعيدًا عن سلوك السوائل الحقيقية حتى يكون مفيدًا. ومع ذلك ، فهي لا تزال أقل صلابة بكثير من العديد من السيناريوهات المبسطة التي اعتبر العلماء في السابق معادلات أويلر. في الواقع ، أظهر Elgindi أنه في ظل هذه الظروف المبسطة - ولكن ليس كثيرًا - تبدأ معادلات Euler في تحقيق نتائج غير متوقعة.
انتهت اللعبة
لفهم اكتشاف الجندي ، تخيل وعاء من الماء. هذا ليس مثالًا دقيقًا ، نظرًا لأن عمل Elgindi يعتبر السوائل التي ليس لها حدود ، أي أنها تطير مثل فقاعة في درجة انعدام الجاذبية. ولكن من أجل تصور السيناريو ، الذي يقع في مركز عمله ، سيكون من المفيد ترتيب الماء في الخزان. رغم أن أهم الفرضيات الرياضية - وتلك الأكثر صعوبة في إثباتها - تتعلق بالسوائل دون حدود.
ثم تخيل حلقتين كثيفتين من الماء تقعان عند نهايات مختلفة من الخزان. إنها تشكل قمعًا صغيرًا ، مثل الدوامات - الاضطرابات المنظمة داخل السائل. توجد ظواهر مماثلة في الطبيعة ، وتشبه حلقات الدخان التي يمكن للمدخنين ذوي الخبرة أن يعطوها.
تخيل الآن كيف تتجمع حلقتان متعارضتان.
خلال هذا النهج ، تعمل معادلات أويلر بشكل طبيعي ، حيث تقوم بحساب حقول السرعة التي تصف السائل في كل لحظة من الزمن. ولكن عندما يقترب كل منهما معًا ، تبدأ المعادلات في الحصول على نتائج غريبة جدًا.
يوضحون كيف تبدأ الحلقات في الانجذاب لبعضها البعض أكثر وأكثر - ويتم جذب النقاط المركزية للحلقات لبعضها البعض أكثر من الأجزاء الخارجية. نتيجة لذلك ، يتم تمديد الخواتم ، وتبدأ لتشبه القمع. وكلما اقتربت مراكز الخواتم ، زادت سرعتها. ثم يصطدمون.
وإذا نظرت في هذه اللحظة إلى حقل السرعة الذي يصف التصادم ، يمكنك أن ترى أنه مع هذه المجموعة من الافتراضات في تاريخ معادلات أويلر بأكملها ، لم يرها أحد: التفرد. أثبت الجندي أن معادلات أويلر تعطي سرعة لا نهائية عند نقطة التصادم. انتهت اللعبة.
قال الجندي: "الشكل الكلاسيكي للمعادلة ينهار". "بعد ذلك ، ليس من الواضح ما الذي يجري".
النتيجة لها حدودها. وهي أنه من المستحيل تقدير سلوك معادلات أويلر في ظروف "سلسة" تمامًا بناءً على هذه النتيجة. لقد أثبت علماء الرياضيات منذ عدة عقود أنه في ظل ظروف "سلسة" ، فإن السيناريو الذي نظر فيه الجندي لن يسفر عن تفرد.
ومع ذلك ، فإن بقية نتيجته تغير تماما وجهة نظر علماء الرياضيات على هذه المعادلات القديمة.
قبل عمل الجندي ، لم يستطع علماء الرياضيات إثبات وجود أي موقف في السائل دون حدود ، حيث تعمل معادلات أويلر لبعض الوقت (في حين تتجمع الحلقات) ، ولكن ليس إلى ما لا نهاية. في جميع الأعمال السابقة ، تبين أن علماء الرياضيات إذا كانت المعادلات تعمل بشكل أساسي ، فهم يعملون دائمًا.
"هذه نتيجة رائعة للغاية ، لأنها تثبت وجود حالات تفرد في السيناريو ، والتي نسميها" محددة بشكل صحيح "." هذا أمر منطقي ، لكن في الوقت نفسه وصلنا إلى التفرد في وقت محدد "، قال قنسطنطين.
تبحث أجيال عديدة من العلماء عن نقطة ضعف في معادلات أويلر. وأخيرا - مع بعض التحفظات - وجده عالم الرياضيات.