حول المعنى الهندسي للرموز الرمادية

الرموز الرمادية لها صلة وثيقة مع منحنى هيلبرت .

ومع ذلك ، عند التواصل مع الزملاء اتضح أن هذا الإدمان البسيط ينظر في نظرهم إلى شيء غير تافه. البحث عبر الإنترنت لم يقدم أي شيء سوى عبارة موحلة على الويكي: "منحنيات هيلبرت في مسافات ذات أبعاد أكبر هي ممثل لتعميمات الرموز الرمادية". لذلك ، كانت هناك رغبة في فتح الموضوع - باختصار ، بلغة بسيطة.

نتيجة لذلك ، في إطار "فضائح ، مؤامرات ، تحقيقات".

الميزة الرئيسية للرمز الرمادي هي أن قيمتين متجاورتين معجميا تختلفان فقط في فئة واحدة. من ناحية أخرى ، يكون منحنى Hilbert مستمرًا - المسافة بين نقطتين متجاورتين دائمًا واحدة. هذا وحده يلمح إلى علاقتهم الداخلية.

يصف الكود الرمادي تكرارات منحنى هيلبرت داخل فرط مكعب واحد. في الواقع ، إذا أخذنا شفرة 3 بت وقمنا برسمها في مساحة ثلاثية الأبعاد (مع أخذ كل بت للإحداثي المقابل) ، سنحصل على


الشكل 1 الشكل 3 بت رمز رمادي باعتباره مكعب 3 الأبعاد

الصورة المألوفة هي البسيط ثلاثي الأبعاد لمنحنى هيلبرت! استبدال كل عقدة في simplex بالتتابع البسيط (مع مراعاة التدوير والانعكاسات للحفاظ على الاستمرارية) ، حصلنا على منحنى Hilbert 4x4x4.

مواصلة هذه التكرارات ، يمكننا باستمرار ملء شعرية مكعب من أي حجم.


الشكل 2 الشكل 2. العديد من التكرار البسيط لمنحنى هيلبرت.

ولكن كيف حدث ذلك؟

من المعروف أن كود Gray يشبه نفسه. يُطلق عليه أحيانًا نسخة متطابقة "نظرًا لحقيقة أن النصف الأول من القيم عند تغيير الترتيب يعادل النصف الثاني ، باستثناء البتة العالية. الشيء الأكثر أهمية هو مقلوب ببساطة ". من أجل الوضوح ، يعتبر الكود 3 بت أهم جزء - أقصى اليسار:



بما أننا نتحدث عن التشابه الذاتي ، فلنبدأ من البداية - برمز واحد بت. بالمعنى الدقيق للكلمة ، سيكون من الممكن البدء ببعد صفري - النقاط ، هذا لا يغير شيئًا أساسيًا ، فقط الكلمات يجب أن تكتب أكثر.

رمز غراي المكون من رقم واحد أبسط من بندقية ثلاثية الأسطر ، فهو إما 0 أو 1.

هندسيا ، وهذا يتوافق مع مكعب وحدة أحادية البعد - قطعة. يمكنك التنقل على طول مقطع إما من البداية إلى النهاية ، أو من النهاية إلى البداية - حتى التماثل ، هذا واحد. ولكن مع ذلك ، سوف نسمي البداية بالمكان الذي تكون فيه القيمة أقل (تذكر أن جوانب المكعب هي أرقام من الرقم) ، والنهاية - حيث تكون أكثر.

ننتقل إلى حالة ثنائية الأبعاد. مكعب ثنائي الأبعاد هو مربع. مع الأخذ في الاعتبار التشابه الذاتي ، نقوم باستنساخ المكعب أحادي البعد (0،1) ونحصل على قسمين - (0،0 -> 1،0) و (0،1 -> 1،1). أنت الآن بحاجة إلى توصيل هذه الشرائح للالتفاف حول الساحة. وهنا يبرز خياران:

• نربط بداية التكرار السابق - المكعب أحادي البعد مع بداية استنساخه. حتى التماثل ، هذا هو نفس الاتصال بين النهاية والنهاية. نوع التماثل هو المرآة. هذا الخيار يسمى الشرطي "التبشيري".
  
• نحن نربط نهاية التكرار السابق مع بداية استنساخ لها. حتى التماثل ، هذا هو نفس الربط بين بداية السطر ونهاية الاستنساخ. نوع التماثل هو المركزية. نحن نسمي هذا الخيار "قطار".

نحن نتصرف بالمثل في نقل الحالات الثلاث أو أكثر من الأبعاد.


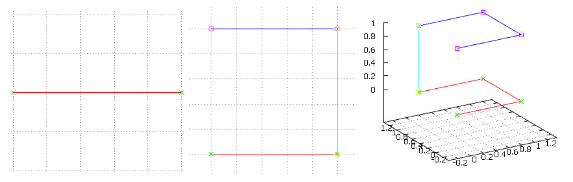الشكل 3 التكرار الأولين من الإصدار "التبشيري"

هنا يتم تمييز التكرار السابق باللون الأحمر ، ويكون استنساخه باللون الأزرق ، ويتم ربطه باللون الفيروزي.

لاحظ أن الاتصال يمر دائمًا بعدًا واحدًا - البعد المضافة حديثًا ، ومن هنا تظهر الميزة الرئيسية لرمز Gray بسبب التشابه الذاتي. ونظرًا لأن نهاية التكرار السابق متصلة بنهاية استنساخها ، تحدث "النسخ المتطابق" - عند الدوران ، نضطر إلى المرور عبر الاستنساخ بترتيب عكسي. بغض النظر عن البعد. هنا يمكنك رؤية أصل وملامح منحنى Hilbert - بغض النظر عن حجم الشبكة (من أي بعد) ، لا يزال على مستوى القواعد الشعبية نفس وحدة المكعب مع التحولات بطول واحد.


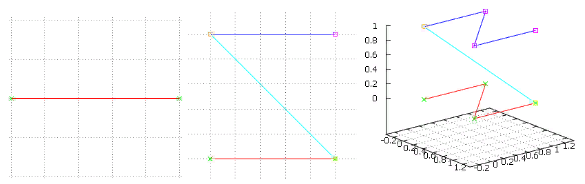الشكل 4 التكرار الأولين للخيار "قطار" ، نفس الألوان

لكن هذه الموسيقى مألوفة لنا أيضًا - لقد حصلنا على منحنى بسيط من نوع Z. تعني كلمة simplex هنا أيضًا أنه إذا أخذنا كل نقطة من نقاطها واستبدلناها بكلمة simplex ، فسوف نحصل على مكعب 4x4 × 4 ، متكررًا - يمكننا ملء شبكة كبيرة مكعب بشكل تعسفي.

من المضحك أنه في هذه الحالة ، يكون تحويل المسار الذي تم تمريره من الأصل إلى الكود ، والذي يمكن تحليله إلى أجزاء صغيرة ، تافهاً.
في حين أن حالة الكود الرمادي هي G = W ^ (W >> 1) ، حيث W هو الطول الذي تم تمريره ، G هي الكود الرمادي.


الشكل 5 التكرار الأولين من منحنى Z (ويكي)


6 للمقارنة ، أول تكرارات لمنحنى هيلبرت (ويكي)

ولكن لا توجد خيارات أخرى (طبيعية) للتحايل على فرط مكعب واحد.
لذلك اتضح أنه أينما ترمي ، حول هيلبرت ، ليبسج ... والفراغ .

ملاحظة : في صورة العنوان ، تشفير دائري مع رمز رمادي مكون من ثمانية أرقام.
PPS : هنا يصححوني أن البساطة هي مصطلح راسخ ، إنه ليس جيدًا. حسنًا ، هذه المقالة ليست مجرد simplex ، ولكنها مجرد منحنى Hilbert أو simplex من منحنى Z. قد يغفر لي علماء الرياضيات المؤمنين.