نظرية المعلومات المرئية (الجزء الثاني)

الجزء الثاني من ترجمة Longrid المكرسة لتصور المفاهيم من نظرية المعلومات. الجزء الثاني يتناول الانتروبيا ، الانتروبيا ، التباعد Kullback-Leibler ، المعلومات المتبادلة والكسور. يتم توفير جميع المفاهيم مع تفسيرات بصرية ممتازة.

للتأكد من اكتمال الإدراك ، قبل قراءة الجزء الثاني ، أوصي بأن تتعرف على الجزء الأول .

حساب الانتروبيا

أذكر أن تكلفة الرسالة طويلة $$$L$ يساوي $$$\ frac {1} {2 ^ L}$ . يمكننا قلب هذه القيمة للحصول على طول الرسالة التي تستحق المبلغ المحدد: $$$\ log_2 (\ frac {1} {cost})$ . لأننا ننفق $$$p (x)$ لكل كلمة مرور لـ $$$x$ ، طول سيكون متساويا $$$\ log_2 (\ frac {1} {p (x)})$ . في الشكل ، واختيار أفضل أطوال الكلمات رمز.



لقد ناقشنا سابقًا أن هناك حدًا أساسيًا لمدى قصر مدة الرسالة على نقل الأحداث من توزيع احتمال معين $$$ع$ . يسمى هذا الحد ، وهو متوسط ​​طول الرسالة عند استخدام أفضل نظام ترميز ، إنتروبي $$$p ، H (p)$ . الآن بعد أن عرفنا طول كلمة المرور الأمثل ، يمكننا حسابه!

$$

$$H (p) = \ sum_xp (x) \ log_2 \ Bigg (\ frac {1} {p (x)} \ Bigg)$$

(في كثير من الأحيان ، هو مكتوب الانتروبيا كما $$$H (p) = - \ sum p (x) \ log_2 (p (x))$ باستخدام المساواة $$$\ log (1 / a) = - \ log (a)$ . يبدو لي أن الإصدار الأول أكثر سهولة ، لذلك سنستمر في استخدامه.)

إذا أردت الإبلاغ عن الحدث الذي حدث ، فبغض النظر عن ما أقوم به ، أحتاج في المتوسط ​​إلى إرسال الكثير من البتات.

متوسط ​​كمية المعلومات اللازمة لنقل شيء ما له عواقب مباشرة على الضغط. ولكن هل هناك أسباب أخرى لماذا يجب أن نعتني بهذا؟ نعم! يصف حالة عدم اليقين الخاصة بي ، ويجعل من الممكن تحديد المعلومات.

إذا كنت أعرف بالتأكيد ما الذي سيحدث ، فلن أضطر إلى إرسال رسالة على الإطلاق! إذا كان هناك شيئان يمكن أن يحدثا باحتمال 50٪ ، فأنا فقط بحاجة لإرسال 1 بت. ولكن إذا كان هناك 64 حدثًا مختلفًا يمكن أن يحدث بنفس الاحتمال ، فسوف يتعين علي إرسال 6 بتات. كلما كان الاحتمال أكثر تركيزًا ، زادت الفرص المتاحة لي لإنشاء رمز ذكي مع رسائل متوسطة قصيرة. كلما كان الاحتمال أكثر غموضًا ، كلما طالت مدة مشاركاتي.

كلما كانت النتيجة غير مؤكدة ، كلما تعلمت أكثر في المتوسط ​​عندما أخبروني بما حدث.

عبر الانتروبيا

قبل فترة وجيزة من الانتقال إلى أستراليا ، تزوج بوب أليس ، وهمي أيضا. لدهشتي ، وكذلك لمفاجأة الشخصيات الأخرى في رأسي ، لم تكن أليس محببة للكلاب. كانت محببة القط. على الرغم من ذلك ، فقد تمكنوا من إيجاد لغة مشتركة في هوسهم العام بالحيوانات والمفردات الخاصة بهم محدودة للغاية.



هذان يستخدمان نفس الكلمات ، فقط بترددات مختلفة. يتحدث بوب عن الكلاب طوال الوقت ، تتحدث أليس عن القطط طوال الوقت.

أرسلت إليّ أولاً رسائل باستخدام رمز بوب. لسوء الحظ ، كانت مشاركاتها أطول من اللازم. تم تحسين رمز Bob لتوزيع الاحتمالات له. أليس لديها توزيع احتمالي مختلف ، والكود ليس هو الأمثل لها. يبلغ متوسط ​​طول كلمة المرور عندما يستخدم بوب الشفرة 1.75 بت ؛ وعندما تستخدمها أليس ، ثم 2.25. سيكون الأمر أسوأ إذا لم يكن الاثنان متشابهان!

ويطلق على متوسط ​​طول الرسالة من توزيع واحد مع الكود الأمثل لتوزيع آخر عبر إنتروبيا. بشكل رسمي ، يمكننا تحديد إنتروبيا على النحو التالي:

$$

$$H_p (q) = \ sum_xq (x) \ log_2 \ Bigg (\ frac {1} {p (x)} \ Bigg)$$

في هذه الحالة ، نحن نتحدث عن الانتروبيا لكلمة تردد كلمة catworm من أليس فيما يتعلق بتكرار كلمة عاشق Bob's dog.



لتقليل تكلفة اتصالنا ، طلبت من Alice استخدام الكود الخاص بها. مما يخففني ، وهذا خفض متوسط ​​طول الرسالة. ولكن هذا خلق مشكلة جديدة: في بعض الأحيان استخدم بوب بطريق الخطأ رمز أليس. من المثير للدهشة أن الأمر أسوأ عندما يستخدم بوب رمز أليس بدلاً من عندما يستخدم أليس رمز بوب!

حتى الآن لدينا أربعة احتمالات:

• يستخدم بوب الرمز الأصلي ( $$$H (ع) = 1.75 دولا$ بت)
• أليس تستخدم كود بوب ( $$ بت)
• أليس تستخدم كودها الخاص ( $$$H (ف) = 1.75 دولا$ بت)
• يستخدم بوب رمز أليس ( $$ بت)

هذه ليست بديهية كما قد يعتقد المرء. على سبيل المثال ، يمكننا أن نرى ذلك $$$H_p (ف) ≠ H_q (p)$ . هل يمكننا أن نرى بطريقة ما مدى ارتباط هذه المعاني الأربعة ببعضها البعض؟

في الرسم البياني التالي ، يمثل كل رسم فرعي أحد هذه الاحتمالات الأربعة. تصور الرسوم التوضيحية متوسط ​​طول الرسالة. يتم تنظيمها في مربع ، بحيث إذا كانت الرسائل من نفس التوزيع ، فإن المخططات تكون قريبة ، وإذا كانت تستخدم نفس الرموز ، فهي في مقدمة بعضها البعض. يتيح لك هذا الجمع بين التوزيعات والرموز بصريا.



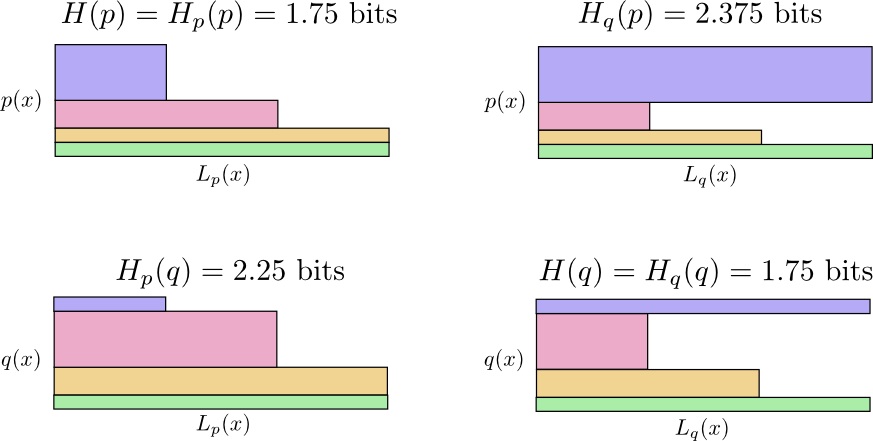
انظر لماذا $$$H_p (ف) ≠ H_q (p)$ ؟ $$$H_q (p)$ كبير جدًا ، لأن الحدث المميز باللون الأزرق غالبًا ما يحدث عندما $$$ع$ ولكن يحصل على كلمة مرور طويلة لأنه أمر نادر للغاية ل $$$ف دولا$ . من ناحية أخرى ، أحداث متكررة مع $$$ف دولا$ أقل شيوعا مع $$$ع$ لكن الفرق هو أقل درامية ، لذلك $$ أقل قليلا.

الانتروبيا المتقاطعة ليست متماثلة.

فلماذا يجب أن تهتم إنتروبيا؟ يعطينا إنتر إنترناشيونال طريقة للتعبير عن مدى اختلاف توزيعات الاحتمال. كلما كانت التوزيعات مختلفة $$$ع$ و $$$ف دولا$ أكبر الانتروبيا $$$ع$ حول $$$ف دولا$ سيكون هناك المزيد من الانتروبيا $$$ع$ .



وبالمثل أكثر من ذلك $$$ف دولا$ يختلف عن $$$ع$ أكبر الانتروبيا $$$ف دولا$ حول $$$ع$ سيكون هناك المزيد من الانتروبيا $$$ف دولا$ .

الشيء المثير للاهتمام حقًا هو الفرق بين الانتروبيا وعبر الكون. هذا الاختلاف يساوي طول مدة مشاركاتنا ، لأننا استخدمنا الكود الأمثل لتوزيع آخر. إذا كانت التوزيعات متماثلة ، فسيكون هذا الاختلاف صفرًا. مع زيادة الاختلافات ، سوف تصبح أكبر.

نحن نسمي هذا الاختلاف Kullback-Leibler التباعد ، أو ببساطة الاختلاف KL. الاختلاف KL $$$ع$ حول $$$ف دولا$ . $$$D_q (p)$ المعرفة على النحو التالي:

$$

$$D_q (p) = H_q (p) - H (p)$$

إن الشيء العظيم في اختلاف KL هو أنه يشبه المسافة بين توزيعتين. إنه يقيس مدى اختلافهم! (إذا أخذت هذه الفكرة على محمل الجد ، فسوف تأتي إلى هندسة المعلومات.)

إن الإنتروبيا و التباعد KL مفيدان بشكل لا يصدق في التعلم الآلي. غالبًا ما نريد توزيعًا ما ليكون قريبًا من الآخر. على سبيل المثال ، قد نود أن يكون التوزيع المتوقع قريبًا من الحقيقة الأساسية. انحراف KL يعطينا طريقة طبيعية للقيام بذلك ، وبالتالي يتجلى في كل مكان.

الانتروبيا والعديد من المتغيرات

دعنا نعود إلى مثال الطقس وملابسنا المعطاة مسبقًا:




أمي ، مثل العديد من الآباء ، تقلق أحيانًا من أنني لا أرتدي ملابس مناسبة للطقس. (لديها سبب وجيه للشك - أنا في بعض الأحيان لا أرتدي معطف واق من المطر في فصل الشتاء.) لذلك ، غالباً ما تريد معرفة الطقس وما أرتديه. كم عدد البتات التي يجب أن أرسلها للإبلاغ عن هذا؟

أسهل طريقة للتفكير في هذا الأمر هي الخروج بتوزيع الاحتمالات:



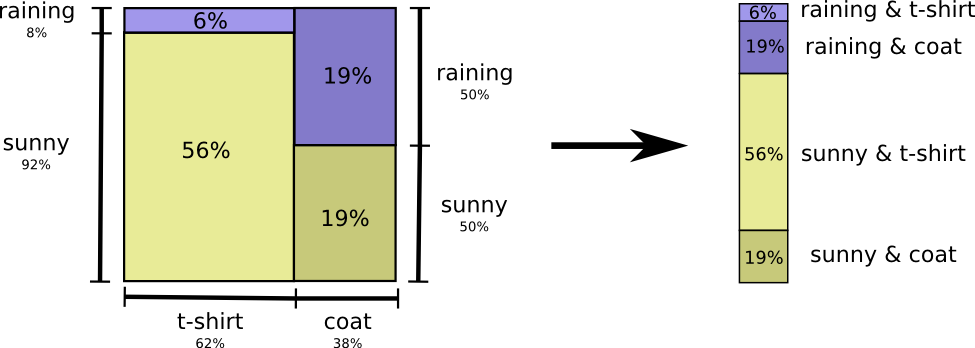
يمكننا الآن حساب كلمات الكود المثلى للأحداث التي تتضمن هذه الاحتمالات وحساب متوسط ​​طول الرسالة:



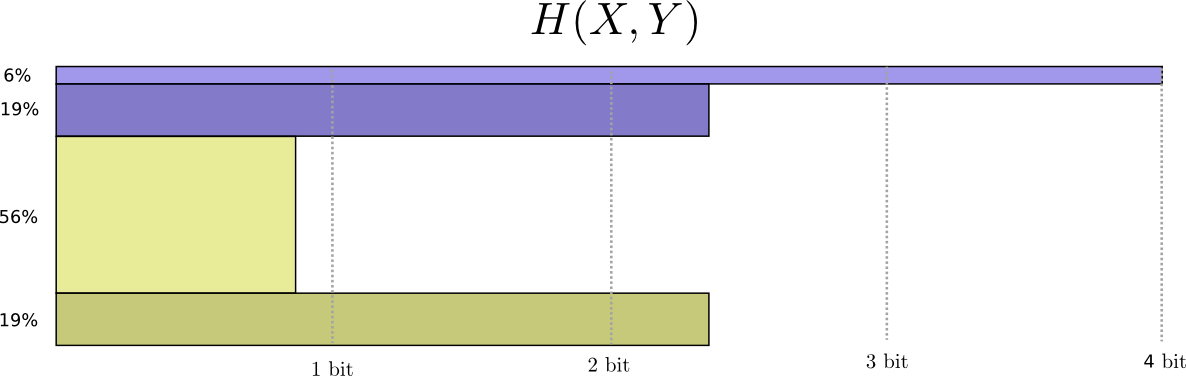
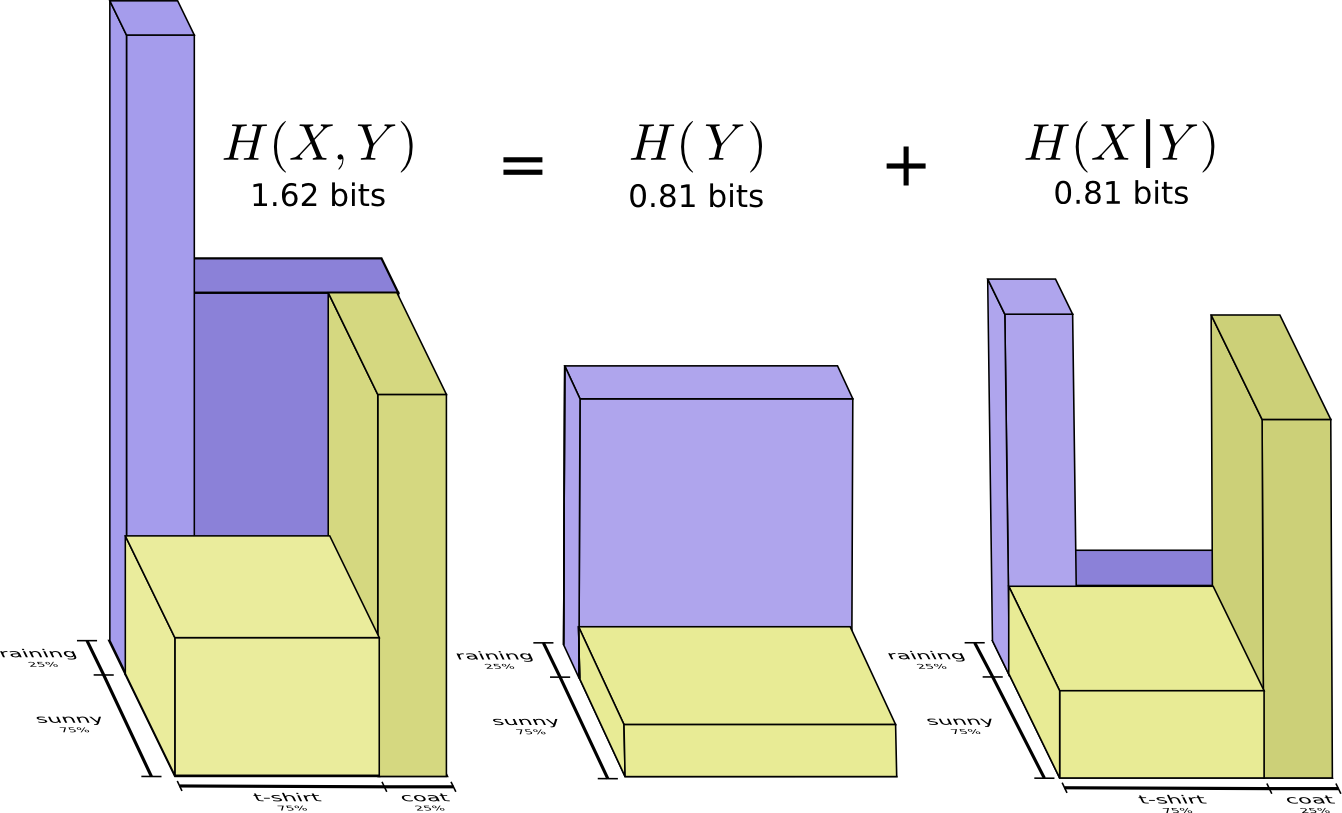
نحن نسميها إنتروبيا مشتركة $$$X$ و $$$Y$ المعرفة على النحو التالي:

$$

$$H (X، Y) = \ sum_ {x، y} p (x، y) \ log_2 \ bigg (\ frac {1} {p (x، y)} \ bigg)$$

يتزامن مع تعريفنا المعتاد ، باستثناء اثنين من المتغيرات بدلا من واحد.

يتم الحصول على صورة أفضل قليلاً من هذا ، دون معادلة التوزيع ، بتمثيل طول كلمة الكود في البعد الثالث. الآن الانتروبيا هو الحجم!



لكن لنفترض أن والدتي تعرف بالفعل الطقس. يمكنها مشاهدتها في الأخبار. ما مقدار المعلومات التي أحتاج إلى تقديمها؟

يبدو أنني بحاجة إلى إرسال معلومات كافية لإخباري بالملابس التي أرتديها. ولكن في الواقع ، أحتاج إلى إرسال معلومات أقل ، لأن الطقس الذي سأرتديه يعتمد بشكل كبير على الطقس! دعونا ننظر في حالة المطر والشمس بشكل منفصل.



في كلتا الحالتين ، لست بحاجة إلى إرسال الكثير من المعلومات في المتوسط ​​، لأن الطقس يعطيني تخمين جيد حول ماهية الإجابة الصحيحة. عندما الشمس ، يمكنني استخدام رمز خاص الأمثل للشمس ، وعندما تمطر ، يمكنني استخدام رمز الأمثل للمطر. في كلتا الحالتين ، أرسل معلومات أقل مما إذا كنت قد استخدمت كودًا مشتركًا لكليهما. للحصول على متوسط ​​كمية المعلومات التي أحتاج إلى إرسالها إلى والدتي ، وضعت للتو هاتين الحالتين معًا ...



نحن نسمي هذا الانتروبيا الشرطية. إذا قمت بإضفاء الطابع الرسمي عليه في معادلة ، فستحصل على:

$$

$$H (X | Y) = \ sum_yp (y) \ sum_xp (x | y) \ log_2 \ bigg (\ frac {1} {p (x | y)} \ bigg)$$

$$

$$= \ sum_ {x، y} p (x، y) \ log_2 \ bigg (\ frac {1} {p (x | y)} \ bigg)$$

معلومات متبادلة

في القسم السابق ، اكتشفنا أن معرفة متغير واحد قد تعني أن هناك حاجة إلى معلومات أقل لتوصيل قيمة متغير آخر.

من الطرق الجيدة للتفكير في الأمر تخيل مقدار المعلومات في شكل خطوط. تتداخل هذه النطاقات إذا كانت هناك معلومات شائعة بينها. على سبيل المثال ، بعض المعلومات في $$$X$ و $$$Y$ مشترك لذلك $$$H (X)$ و $$$H (Y)$ تتداخل المشارب. ومنذ ذلك الحين $$$H (X ، Y)$ هي معلومات كلا المتغيرين ، ثم هذا هو اتحاد العصابات $$$H (X)$ و $$$H (Y)$ .



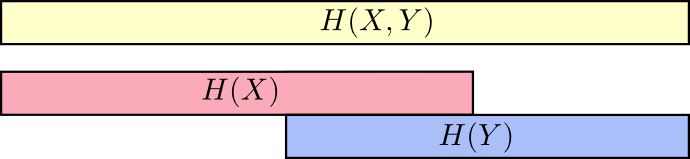
عندما نفكر في الأشياء بهذه الطريقة ، يصبح من الأسهل رؤيتها.

على سبيل المثال ، لاحظنا بالفعل أن لنقل المعلومات كما $$$X$ و و $$$Y$ ("الانتروبيا المشتركة" ، $$$H (X ، Y)$ ) مزيد من المعلومات مطلوبة من أجل الإرسال فقط $$$X$ ("الانتروبيا النهائية" ، $$$H (X)$ ). ولكن إذا كنت تعرف بالفعل $$$Y$ ثم للإرسال $$$X$ ("الكون الشرطي" ، $$$H (X | Y)$ ) معلومات أقل مطلوبة مما إذا كنت لا تعرف هذا!



يبدو الأمر معقدًا ، ولكن إذا قمت بالترجمة إلى فرق ، فسيظهر كل شيء في غاية البساطة. $$$H (X | Y)$ هي المعلومات التي يجب أن نرسلها من أجل إبلاغ $$$X$ الشخص الذي يعرف بالفعل $$$Y$ المعلومات في $$$X$ وهو أيضا ليس في $$$Y$ . بصريا ، وهذا يعني ذلك $$$H (X | Y)$ - هذا جزء من الشريط $$$H (X)$ الذي لا يتداخل مع $$$H (Y)$ .

الآن يمكنك قراءة عدم المساواة $$$H (X، Y) ≥H (X) ≥H (X | Y)$ مباشرة على الرسم البياني التالي.



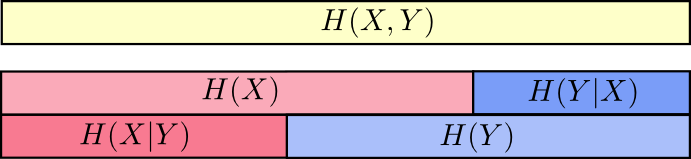
مساواة أخرى هي كما يلي - $$$H (X، Y) = H (Y) + H (X | Y)$ . أي المعلومات في $$$X$ و $$$Y$ هذه هي المعلومات في $$$Y$ بالإضافة إلى المعلومات في $$$X$ وهو ليس في $$$Y$ .



مرة أخرى ، يصعب رؤية ذلك في المعادلات ، لكن من السهل معرفة ما إذا كنت تفكر في تداخل نطاقات المعلومات.

في هذه المرحلة ، قمنا بتقسيم المعلومات إلى $$$X$ و $$$Y$ بعدة طرق. نحن نعرف المعلومات في كل متغير ، $$$H (X)$ و $$$H (Y)$ . نحن نعرف مزيج من المعلومات في كليهما $$$H (X ، Y)$ . لدينا معلومات في متغير واحد ولكن ليس في متغير آخر ، $$$H (X | Y)$ و $$$H (Y | X)$ . يدور الكثير من هذا حول المعلومات الشائعة للمتغيرات - تقاطع معلوماتهم. نحن نسميها "معلومات متبادلة" $$$I (x، y)$ يعرف بأنه:

$$

$$I (X، Y) = H (X) + H (Y) −H (X، Y)$$

هذا التعريف صحيح لأنه $$$H (X) + H (Y)$ يحتوي على نسختين من المعلومات المتبادلة ، لأنه موجود أيضًا في $$$X$ وفي $$$Y$ ، في حين أن $$$H (X ، Y)$ يحتوي على نسخة واحدة فقط. (انظر الرسم البياني السابق)

يرتبط اختلاف المعلومات ارتباطًا وثيقًا بالمعلومات المتبادلة. تباين المعلومات هو المعلومات غير الشائعة للمتغيرات. يمكننا تعريفها مثل هذا:

$$

$$V (X، Y) = H (X، Y) −I (X، Y)$$

تباين المعلومات مثير للاهتمام لأنه يعطينا مقياسًا ، هو مفهوم المسافة بين المتغيرات المختلفة. يكون تباين المعلومات بين متغيرين صفراً إذا كانت معرفة قيمة أحد المتغيرات تخبرك بمعنى الآخر وتصبح أكبر كلما أصبحت أكثر استقلالية.

كيف يرتبط هذا بانحراف KL ، والذي يعطينا أيضًا مفهوم المسافة؟ الاختلاف KL هو المسافة بين توزيعتين على نفس المتغير أو مجموعة من المتغيرات. على العكس من ذلك ، فإن تنوع المعلومات يعطينا المسافة بين متغيرين مشتركين في التوزيع. اختلاف KL هو تباين بين التوزيعات ، وهو تباين في المعلومات داخل التوزيع.

يمكننا تجميعها جميعًا في مخطط واحد يربط بين هذه الأنواع المختلفة من المعلومات:

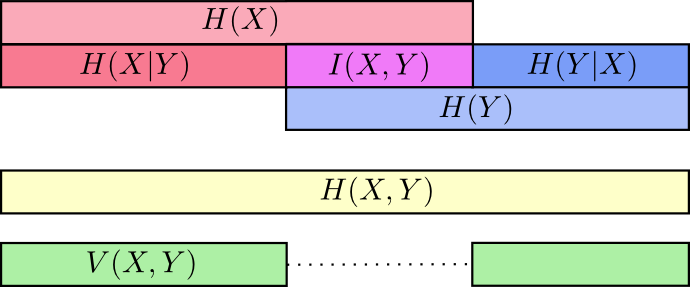
بت جزء

الشيء غير الحدسي للغاية في نظرية المعلومات هو أنه يمكن أن يكون لدينا أعداد كسرية من البتات. هذا غريب جدا. ماذا يعني نصف قليلا؟

فيما يلي إجابة بسيطة: غالبًا ما نرغب في متوسط ​​طول الرسالة ، بدلاً من طول رسالة معينة. إذا تم إرسال بت واحد في نصف الحالات ، وفي نصف الحالات اثنان ، يتم إرسال بت واحد ونصف في المتوسط. لا يوجد شيء غريب في حقيقة أن المتوسطات يمكن أن تكون كسرية.

ولكن مع هذه الإجابة نخجل من السؤال. في كثير من الأحيان أطوال الكودورد الأمثل هي أيضا كسور. ماذا يعني هذا؟

لنكون محددين ، دعنا ننظر إلى توزيع الاحتمالات ، حيث حدث واحد ، $$$دولا$ يحدث 71 ٪ من الوقت ، وحدث آخر ، $$$ب$ يحدث 29 ٪ من الوقت.



سيستخدم الرمز الأمثل 0.5 بت لتمثيل $$$دولا$ و 1.7 بت لتمثيل $$$ب$ . حسنًا ، إذا أردنا إرسال كلمة واحدة فقط من هذه الأكواد البرمجية ، فهذا التمثيل مستحيل. نحن مضطرون للتقريب إلى عدد صحيح من البتات وإرسال متوسط ​​1 بت.

... ولكن إذا أرسلنا العديد من الرسائل في نفس الوقت ، فقد اتضح أننا نستطيع أن نفعل ما هو أفضل. دعونا ننظر في نقل حدثين من هذا التوزيع. إذا أرسلناهم بشكل مستقل ، فسيتعين علينا إرسال جزئين. كيف يمكننا تحسين هذا؟



في نصف الحالات نحتاج إلى إرسال $$$أأ دولا$ ، في 21 ٪ من الحالات - $$$ab$ أو $$$ba$ وفي 8٪ من الحالات - $$$ب ب دولا$ . مرة أخرى ، رمز مثالي يتضمن البتات الكسرية.



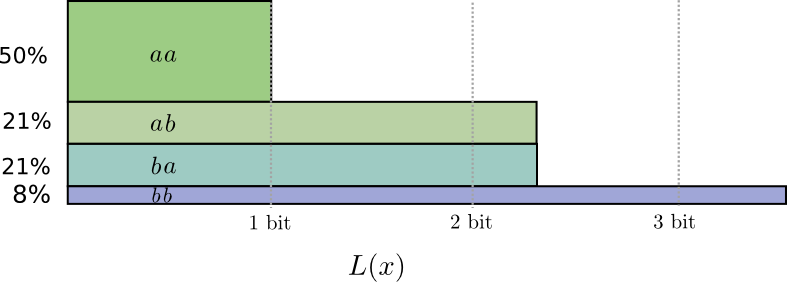
إذا قمنا بإغلاق أطوال الكود ، فسوف نحصل على شيء مثل هذا:



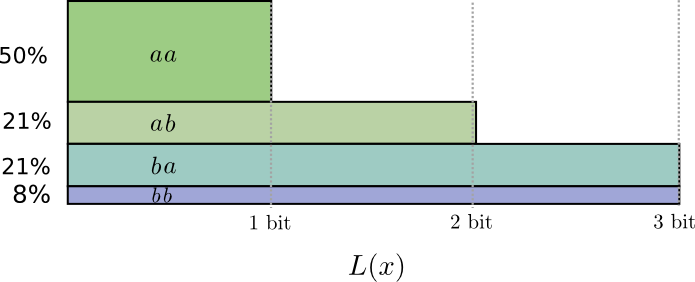
هذه الرموز تعطينا متوسط ​​طول الرسالة 1.8 بت. هذا أقل من 2 بت عندما نرسل الرسائل بشكل مستقل. أي في هذه الحالة ، نرسل 0.9 بت في المتوسط ​​لكل حدث. إذا أرسلنا المزيد من الأحداث في وقت واحد ، فسيكون المتوسط ​​أقل. في $$$ن$ تميل النفقات العامة المرتبطة بتقريب الكود الخاص بنا إلى النهاية ، وسوف يتقارب عدد البتات لكل كلمة مرور إلى الإنتروبيا.

بعد ذلك ، لاحظ أن طول الكودود المثالي لهذا الحدث $$$دولا$ كان 0.5 بت ، والطول المثالي لكلمة الترميز $$$أأ دولا$ - 1 بت. أطوال الكودورد المثالي تضيف ما يصل ، حتى لو كانت كسرية! لذلك ، إذا قمنا بالإبلاغ عن العديد من الأحداث في وقت واحد ، فإن الأطوال ستضاف.

كما نرى ، هناك معنى حقيقي للأرقام الكسرية للبت من المعلومات ، حتى لو كانت الأكواد الفعلية يمكنها فقط استخدام الأعداد الصحيحة.

(في الممارسة العملية ، يستخدم الأشخاص مخططات ترميز معينة فعالة في حالات مختلفة. رمز Huffman ، وهو في الواقع نوع من التعليمات البرمجية التي رسمناها هنا ، لا يتعامل مع البتات الكسرية بشكل أنيق للغاية - يجب عليك تجميع الأحرف كما فعلنا أعلاه ، أو استخدام حيل أكثر تعقيدًا للاقتراب من حد الانتروبيا. الترميز الحسابي مختلف قليلاً ، فهو يعالج بأناقة البتات الكسرية لتكون المثلي بدون تناسق.)

استنتاج

إذا كنا نشعر بالقلق إزاء نقل المعلومات لأدنى عدد من البتات ، فإن هذه الأفكار هي بالطبع أساسية. إذا كنا نهتم بضغط البيانات ، فإن نظرية المعلومات تحل المشكلات الرئيسية وتمنحنا التجريدات الصحيحة بشكل أساسي. لكن ماذا لو لم نهتم - أليس هذا غريبًا؟

تظهر أفكار من نظرية المعلومات في العديد من السياقات: التعلم الآلي ، والفيزياء الكمومية ، والوراثة ، والديناميكا الحرارية ، وحتى المقامرة. لا يهتم الممارسون في هذه المناطق بنظرية المعلومات لأنهم يريدون ضغط المعلومات. إنهم يهتمون بأن لديه اتصال لا يقاوم مع منطقتهم. التشابك الكمي يمكن وصفه بالنتروبيا. يمكن الحصول على العديد من النتائج في الميكانيكا الإحصائية والديناميكا الحرارية عن طريق افتراض أقصى قدر من الانتروبيا حول الأشياء التي لا تعرفها. ترتبط أرباح وخسائر اللاعب بشكل مباشر بانحراف KL ، على وجه الخصوص ، الإعدادات المتكررة.

تظهر نظرية المعلومات في كل هذه الأماكن لأنها تقدم شكليات ملموسة وأساسية للعديد من الأشياء التي يجب علينا التعبير عنها. إنه يعطينا طرقًا لقياس والتعبير عن عدم اليقين ، ومدى اختلاف مجموعتي المعتقدات ، وأن إجابة أحد الأسئلة تخبرنا عن الآخر: إلى أي مدى يكون التشتت هو الاحتمال ، والمسافة بين توزيعات الاحتمال ، ومدى الاعتماد على المتغيرين. هل هناك أي أفكار بديلة مماثلة؟ بالطبع لكن الأفكار من نظرية المعلومات نقية ، ولها خصائص جيدة وتستند إلى مبادئ. في بعض الحالات ، هذه الأفكار هي بالضبط ما تحتاجه ، وفي حالات أخرى ، تكون وسيطًا مناسبًا في عالم فوضوي.

التعلم الآلي هو أفضل ما أعرفه ، لذلك دعونا نتحدث عن ذلك دقيقة واحدة. وهناك نوع شائع للغاية من المهام في التعلم الآلي هو التصنيف. لنفترض أننا نريد أن ننظر إلى صورة ونتوقع ما إذا كانت ستكون صورة لكلب أو قطة. قد يقول نموذجنا شيئًا مثل: "هناك احتمال بنسبة 80٪ أن تكون هذه صورة لكلب ، واحتمال بنسبة 20٪ أنها قطة." لنفترض أن الإجابة الصحيحة هي كلب - ما مدى جودة أو سوء ما قلناه أن الاحتمال ما هو الكلب 80 ٪؟ ما هو أفضل من شأنه أن يقول 85 ٪؟

هذا سؤال مهم لأننا نحتاج إلى فكرة عن مدى جودة أو سوء نموذجنا من أجل تحسينه للنجاح. ما ينبغي أن نحسن؟ تعتمد الإجابة الصحيحة فعليًا على ما نستخدمه في النموذج: هل نحن مهتمون فقط بما إذا كان تخميننا صحيحًا ، أم أننا نهتم بمدى ثقتنا في الإجابة الصحيحة؟ما مدى سوء أن تكون مخطئًا بثقة؟ لا يوجد إجابة واحدة صحيحة لهذا. غالبًا ما يكون من المستحيل معرفة الإجابة الصحيحة ، لأننا لا نعرف بالضبط كيف سيتم استخدام النموذج لإضفاء الطابع الرسمي على ما يثيرنا في نهاية المطاف. هناك حالات يكون فيها الانتروبيا هو ما يقلقنا تمامًا ، ولكن هذا ليس هو الحال دائمًا. في كثير من الأحيان ، لا نعرف بالضبط ما يقلقنا ، والعبور العابر هو وكيل جيد حقًا.

المعلومات تعطينا قاعدة جديدة قوية للتفكير في العالم. في بعض الأحيان يكون مثاليا لمهمة معينة. في حالات أخرى ، ليس تماما ، ولكن لا تزال مفيدة للغاية. خدش هذا المقال سطح نظرية المعلومات فقط - فهناك موضوعات رئيسية ، مثل رموز تصحيح الأخطاء ، التي لم نتطرق إليها على الإطلاق ، لكنني آمل أن أثبتت أن نظرية المعلومات موضوع رائع يجب ألا يخيفه.