لماذا فرز سريع بطيئة حقا؟ طريقة فرز صفيف جديدة

يعتقد الكثير من المبرمجين أن Quick Sort هي أسرع خوارزمية على الإطلاق. هذا صحيح جزئيا. ولكنه يعمل بشكل جيد فقط فقط إذا تم تحديد عنصر الدعم بشكل صحيح ( ثم التعقيد هو O (n log n) ). وإلا ، فإن السلوك المقارب سيكون هو نفسه سلوك الفقاعة تقريبًا (على سبيل المثال ، O (n ² ) ).
في الوقت نفسه ، إذا تم فرز المصفوفة بالفعل ، فلن تعمل الخوارزمية بشكل أسرع من O (n log n)

بناءً على ذلك ، قررت أن أكتب خوارزمية خاصة بي لفرز صفيف من شأنه أن يعمل بشكل أفضل من quick_sort. وإذا تم فرز المجموعة بالفعل ، فلا تقم بتشغيلها مجموعة من المرات ، كما هو الحال مع العديد من الخوارزميات.

"لقد كان المساء ، لم يكن هناك شيء نفعله" - سيرجي ميخالكوف.

متطلبات:

1. أفضل حالة يا (ن)
2. متوسط ​​حالة O (n log n)
3. الحالة الأسوأ O (n log n)
4. في المتوسط ​​أسرع من الفرز السريع

الآن دعونا نحصل على كل شيء بالترتيب

من أجل أن تعمل الخوارزمية دائمًا بسرعة ، من الضروري أن يكون السلوك المقارب في الحالة المتوسطة O (n log n) على الأقل ، وفي أفضل الأحوال ، O (n). نعلم جميعًا تمامًا أنه ، في أفضل الأحوال ، يعمل فرز الإدراج مرة واحدة. ولكن في أسوأ الأحوال ، سيكون عليها أن تجوب الصفيف عدة مرات مثل وجود عناصر فيه.

معلومات أولية

int* glue(int* a, int lenA, int* b, int lenB) { int lenC = lenA + lenB; int* c = new int[lenC]; //   int indx_a = 0; int indx_b = 0; int i = 0; for (; i < lenC; ++i) { if (indx_a < lenA) { if (indx_b < lenB) { //     c[i] = (a[indx_a] < b[indx_b]) ? a[indx_a++] : b[indx_b++]; continue; } //      while (indx_a < lenA) c[i++] = a[indx_a++]; } else //      while (indx_b < lenB) c[i++] = b[indx_b++]; break; } return c; } 

 void glueDelete(int*& arr, int*& a, int lenA, int*& b, int lenB) { if (lenA == 0) { //    delete[] a; //     arr = b; //     return; } if (lenB == 0) { //    delete[] b; //     arr = a; //     return; } int *copy = glue(a, lenA, b, lenB); //  delete[]a; //    delete[]b; //    arr = copy; //   } 

 void insertionSort(int*& arr, int lo, int hi) { for (int i = lo + 1; i <= hi; ++i) for (int j = i; j > 0 && arr[j - 1] > arr[j]; --j) swap(arr[j - 1], arr[j]); } 

الإصدار الأولي من الخوارزمية (ليس الأمثل):

الفكرة الرئيسية للخوارزمية هي البحث المزعوم عن الحد الأقصى (والحد الأدنى). في كل تكرار ، حدد عنصرًا من الصفيف. إذا كان أكبر من الحد الأقصى السابق ، فقم بإضافة هذا العنصر إلى نهاية التحديد. خلاف ذلك ، إذا كان أقل من الحد الأدنى السابق ، فإننا نضيف هذا العنصر إلى البداية. خلاف ذلك ، وضعت في مجموعة منفصلة.

تأخذ وظيفة الإدخال صفيفًا وعدد العناصر في هذه المجموعة

 void FirstNewGeneratingSort(int*& arr, int len) 

لتخزين عينة من الصفيف (الارتفاعات والانخفاضات) وعناصر أخرى ، نخصص الذاكرة

 int* selection = new int[len << 1]; //     new int[len * 2] int left = len - 1; //       int right = len; //       int* restElements = new int[len]; //  ,      int restLen = 0; //      

كما ترون ، خصصنا ذاكرة أكثر مرتين لتخزين العينة من صفيفنا الأصلي. يتم ذلك في حالة وجود مصفوفة مرتبة وكل عنصر تالي سيكون بحد أقصى جديد. بعد ذلك ، سيتم شغل الجزء الثاني فقط من مجموعة العينات. أو العكس (إذا تم الفرز بترتيب تنازلي).

لعينة ، تحتاج أولا الحد الأدنى والحد الأقصى الأولي. ما عليك سوى اختيار العناصر الأولى والثانية

 if (arr[0] > arr[1]) swap(arr[0], arr[1]); selection[left--] = arr[0]; selection[right++] = arr[1]; 

أخذ العينات نفسها

 for (int i = 2; i < len; ++i) { if (selection[right - 1] <= arr[i]) //     { selection[right++] = arr[i]; continue; } if (selection[left + 1] >= arr[i]) //     { selection[left--] = arr[i]; continue; } restElements[restLen++] = arr[i]; //      ,    } 

الآن لدينا مجموعة مرتبة من العناصر ، والعناصر "المتبقية" التي ما زلنا بحاجة إلى فرزها. ولكن عليك أولاً القيام ببعض التلاعب بالذاكرة.

تحرير الذاكرة غير المستخدمة

 int selectionLen = right - left - 1; //   int* copy = glue(selection + left + 1, selectionLen, nullptr, 0); //       delete[] selection; //   2 * len ,         ,     selection = copy; //  ,    selection     delete[] arr; //    ,         ,       

قم بإجراء مكالمة فرز متكررة للعناصر المتبقية ودمجها مع التحديد

 FirstNewGeneratingSort(restElements, restLen); glueDelete(arr, selection, selectionLen, restElements, restLen); 

 void FirstNewGeneratingSort(int*& arr, int len) { if (len < 2) return; int* selection = new int[len << 1]; int left = len - 1; int right = len; int* restElements = new int[len]; int restLen = 0; if (arr[0] > arr[1]) swap(arr[0], arr[1]); selection[left--] = arr[0]; selection[right++] = arr[1]; for (int i = 2; i < len; ++i) { if (selection[right - 1] <= arr[i]) //     { selection[right++] = arr[i]; continue; } if (selection[left + 1] >= arr[i]) //     { selection[left--] = arr[i]; continue; } restElements[restLen++] = arr[i]; //      ,    } int selectionLen = right - left - 1; //   int* copy = glue(selection + left + 1, selectionLen, nullptr, 0); //       delete[] selection; //   2 * len ,          ,     selection = copy; //  ,    selection     delete[] arr; //    ,         ,       FirstNewGeneratingSort(restElements, restLen); glueDelete(arr, selection, selectionLen, restElements, restLen); } 

دعونا نتحقق من سرعة الخوارزمية مقارنةً بالفرز السريع

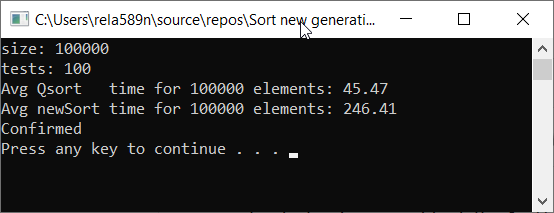
كما ترون ، هذا ليس على الإطلاق ما أردنا. ما يقرب من 6 مرات أطول من QuickSort! لكن في هذا السياق ، من غير المناسب استخدامه ، حيث أنه من غير المقارب ما يهم. في هذا التطبيق للخوارزمية ، في أسوأ الحالات ، سيكون العنصران الأول والثاني هما الحد الأدنى والحد الأقصى. وسيتم نسخ الباقي إلى مجموعة منفصلة.

خوارزمية التعقيد:

• الحالة الأسوأ: O (n ² )
• الحالة الوسطى: O (ن ² )
• أفضل حالة: O (ن)

حسنًا ، هذا ليس أفضل من نفس الفرز بواسطة إدراجات. نعم ، في الواقع يمكننا العثور على الحد الأقصى (الحد الأدنى) للعنصر بسرعة كبيرة ، والباقي ببساطة لن يقع في الاختيار.

يمكننا محاولة تحسين دمج الفرز. أولاً ، تحقق من سرعة دمج الدمج المعتاد:

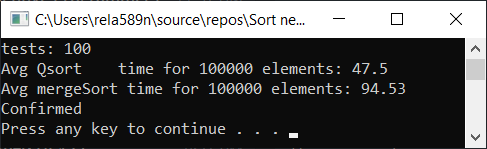
 void newGenerationMergeSort(int* a, int lo, int hi, int& minPortion) { if (hi <= lo) return; int mid = lo + (hi - lo) / 2; if (hi - lo <= minPortion) { //       ,     int* part = glue(a + lo, hi - lo + 1, nullptr, 0); //    FirstNewGeneratingSort(part, hi - lo + 1); for (int i = lo; i <= hi; ++i) { a[i] = part[i - lo]; } delete[] part; return; } newGenerationMergeSort(a, lo, mid, minPortion); newGenerationMergeSort(a, mid + 1, hi, minPortion); int* b = glue(a + lo, mid - lo + 1, a + mid + 1, hi - mid); for (int i = lo; i <= hi; i++) a[i] = b[i - lo]; delete[] b; } 

هناك حاجة إلى نوع من المجمع لسهولة الاستخدام.

 void newMergeSort(int *arr, int length) { int portion = log2(length); //      portion *= portion; newGenerationMergeSort(arr, 0, length - 1, portion); } 

نتيجة الاختبار:

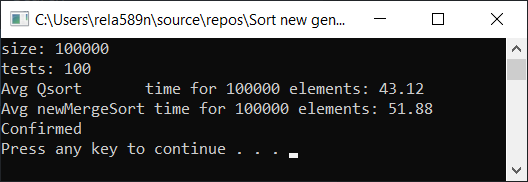
نعم ، لوحظ زيادة في السرعة ، لكن مع ذلك ، هذه الوظيفة لا تعمل بالسرعة السريعة. علاوة على ذلك ، لا يمكننا التحدث عن O (n) في المصفوفات المصنفة. لذلك ، يتم تجاهل هذا الخيار أيضًا.

خيارات التحسين للخيار الأول

1. من أجل ضمان أن التعقيد ليس هو O (n ² ) ، يمكننا إضافة عناصر لم تدخل في العينة ليس في صفيف واحد كما كان من قبل ، ولكن توسيعها إلى صفيفين. بعد ذلك ، يبقى فرز هذين الجزءين فقط ، ودمجهما مع نموذجنا. نتيجة لذلك ، نحصل على تعقيد يساوي O (n log n)

2. كما لاحظنا بالفعل ، يمكن العثور على العنصر (الحد الأدنى) الأقصى في الصفيف المفروض بسرعة كبيرة ، وهذا ليس فعالًا جدًا. هذا هو المكان الذي يأتي فيه فرز الإدراج لمساعدتنا. في كل تكرار من التحديد ، سوف نتحقق مما إذا كنا نستطيع إدراج عنصر التدفق في مجموعة من آخر ، على سبيل المثال ، ثمانية إدراج.

إذا لم يكن الأمر واضحًا الآن ، فلا تنزعج. يجب أن يكون كذلك. الآن سيصبح كل شيء واضحًا في الكود وسوف تختفي الأسئلة.

النسخة الصحيحة المتبقية من الخوارزمية:

التوقيع هو نفسه كما في الإصدار السابق

 void newGenerationSort(int*& arr, int len) 

ولكن تجدر الإشارة إلى أن هذا الخيار يفترض مؤشرًا للمعلمة الأولى التي يمكن أن تسمى عملية الحذف [] (لماذا - سنرى لاحقًا). أي عندما خصصنا الذاكرة ، قمنا بتعيين عنوان بداية الصفيف لهذا المؤشر.

التحضير الأولي

في هذا المثال ، ما يسمى "معامل اللحاق بالركب" هو مجرد ثابت بقيمة 8. ويوضح عدد العناصر القصوى التي نحاول المرور لإدخال "جديد أقل من الحد الأدنى" أو "أقل من الحد الأدنى" في مكانه.

 int localCatchUp = min(catchUp, len); //            insertionSort(arr, 0, localCatchUp - 1); //     localCatchUp  if (len <= localCatchUp) //       n <= catchUp ,   return; //    (      ) 

لتخزين العينة ، قم بإنشاء صفيف

إذا كان هناك شيء غير واضح ، فراجع التوضيح في الإصدار الأولي

 int* selection = new int[len << 1]; //     new int[len * 2] int left = len - 1; //       int right = len; //       

املأ العناصر القليلة الأولى من مجموعة التحديد

 selection[left--] = arr[0]; for (int i = 1; i < localCatchUp; ++i) { selection[right++] = arr[i]; } 

واسمحوا لي أن أذكرك بأن القمم الجديدة تنتقل إلى الجانب الأيسر من مركز مجموعة النماذج ، وتنتقل القمم الجديدة إلى اليمين

إنشاء صفائف لتخزين العناصر غير المحددة

 int restLen = len >> 1; //     len / 2 int* restFirst = new int[restLen]; int* restSecond = new int[restLen]; int restFirstLen = 0; int restSecondLen = 0; 

الآن ، الشيء الأكثر أهمية هو الاختيار الصحيح للعناصر من الصفيف المصدر

تبدأ الدورة بـ localCatchUp (لأن العناصر السابقة قد أدخلت بالفعل نموذجنا باعتباره القيم التي سنبدأ منها). وغني عن النهاية. بعد ذلك ، في النهاية ، سيتم توزيع جميع العناصر إما في صفيف التحديد أو في إحدى صفائف التحديد الأقل.

للتحقق مما إذا كان بإمكاننا إدراج عنصر في التحديد ، سوف نتحقق ببساطة من أنه (أو يساوي) مواضع العنصر 8 على اليسار (يمين - localCatchUp). إذا كانت هذه هي الحالة ، فنحن ببساطة نقوم بإدخالها في الموضع المطلوب مع مرور واحد عبر هذه العناصر. كان هذا للجانب الأيمن ، أي بالنسبة للعناصر القصوى. بنفس الطريقة ، نقوم بالعكس لأدنى حد. إذا لم تتمكن من إدراجه في أي من جانبي التحديد ، فسنقوم بإلقائه في إحدى الصفائف الباقية.

ستبدو الحلقة بشيء من هذا القبيل:

 for (int i = localCatchUp; i < len; ++i) { if (selection[right - localCatchUp] <= arr[i]) { selection[right] = arr[i]; for (int j = right; selection[j - 1] > selection[j]; --j) swap(selection[j - 1], selection[j]); ++right; continue; } if (selection[left + localCatchUp] >= arr[i]) { selection[left] = arr[i]; for (int j = left; selection[j] > selection[j + 1]; ++j) swap(selection[j], selection[j + 1]); --left; continue; } if (i & 1) { // i -  restFirst[restFirstLen++] = arr[i]; } else { restSecond[restSecondLen++] = arr[i]; } } 

مرة أخرى ، ما الذي يحدث هنا؟ أولاً نحاول دفع العنصر إلى أعلى المستويات. لا تعمل - إذا كان ذلك ممكنا ، ورميها في أدنى المستويات. إذا كان من المستحيل القيام بذلك أيضًا - فضعه في الراحة أولاً أو الراحة الثانية.

الجزء الأصعب قد انتهى. الآن ، بعد الحلقة ، لدينا مصفوفة مرتبة مع تحديد (تبدأ العناصر في الفهرس [يسار + 1] وتنتهي في [يمين - 1] ) ، وكذلك صفيف restFirst و restSecond من الطول restFirstLen و restSecondLen ، على التوالي.

كما في المثال السابق ، قبل استدعاء العودية نقوم بتحرير الذاكرة من الصفيف الرئيسي (قمنا بالفعل بحفظ جميع عناصره)

 delete[] arr; 

يمكن أن تحتوي مجموعة التحديد الخاصة بنا على العديد من خلايا الذاكرة غير المستخدمة. قبل مكالمة متكررة ، تحتاج إلى تحريره.

تحرير الذاكرة غير المستخدمة

 int selectionLen = right - left - 1; //     int* copy = glue(selection + left + 1, selectionLen, nullptr, 0); //        delete[] selection; //    2 * len   selection = copy; //      ,   

الآن قم بتشغيل وظيفة الفرز بشكل متكرر للصفيفين restFirst و restSecond

لفهم كيف يعمل ، تحتاج أولاً إلى إلقاء نظرة على الكود حتى النهاية. في الوقت الحالي ، ما عليك سوى تصديق أنه بعد إجراء مكالمات متكررة ، سيتم فرز صفيف restFirst و restSecond.

 newGenerationSort(restFirst, restFirstLen); newGenerationSort(restSecond, restSecondLen); 

وأخيرًا ، نحتاج إلى دمج 3 صفائف في المجموعة الناتجة وتعيينها إلى arr المؤشر.

يمكنك أولاً دمج restFirst + restSecond في بعض الصفيف restFull ، ثم دمج التحديد + restFull . لكن هذه الخوارزمية تحتوي على خاصية من المرجح أن تحتوي صفيف التحديد فيها على عناصر أقل بكثير من أي من صفائف الراحة . افترض أن التحديد يحتوي على 100 عنصر ، بينما يحتوي restFirst على 990 ، بينما يحتوي restSecond على 1010. ثم ، لإنشاء صفيف restFull ، تحتاج إلى تنفيذ 990 + 1010 = 2000 نسخ. ثم للاندماج مع الاختيار - 2000 + 100 نسخة أخرى. المجموع مع هذا النهج ، سيكون إجمالي نسخة 2000 + 2100 = 4100.

دعنا نطبق التحسين هنا. أولاً دمج التحديد و restFirst في صفيف التحديد . نسخ العمليات: 100 + 990 = 1090. بعد ذلك ، قم بدمج التحديد والصفيفات الثانية وقضاء 1090 + 1010 = 2100 نسخة أخرى. في المجموع ، سيتم إصدار 2100 + 1090 = 3190 ، وهو أقل بمقدار الربع تقريبًا عن النهج السابق.

الدمج النهائي للصفائف

 int* part2; int part2Len; if (selectionLen < restFirstLen) { glueDelete(selection, restFirst, restFirstLen, selection, selectionLen); // selection += restFirst selectionLen += restFirstLen; part2 = restSecond; part2Len = restSecondLen; } else { glueDelete(part2, restFirst, restFirstLen, restSecond, restSecondLen); // part2 = restFirst + restSecond part2Len = restFirstLen + restSecondLen; } glueDelete(arr, selection, selectionLen, part2, part2Len); 

كما ترون ، إذا كان من الأفضل لنا دمج الاختيار مع restFirst ، فإننا نفعل ذلك. خلاف ذلك ، ندمج كما في "restFull"

 /// works only if arr is pointer assigned by new keyword void newGenerationSort(int*& arr, int len) { int localCatchUp = min(catchUp, len); //            insertionSort(arr, 0, localCatchUp - 1); //     localCatchUp  if (len <= localCatchUp) //       n <= catchUp  return; //      int* selection = new int[len << 1]; //     new int[len * 2] int left = len - 1; //       int right = len; //       selection[left--] = arr[0]; for (int i = 1; i < localCatchUp; ++i) { selection[right++] = arr[i]; } int restLen = len >> 1; int* restFirst = new int[restLen]; int* restSecond = new int[restLen]; int restFirstLen = 0; int restSecondLen = 0; for (int i = localCatchUp; i < len; ++i) { if (selection[right - localCatchUp] <= arr[i]) { selection[right] = arr[i]; for (int j = right; selection[j - 1] > selection[j]; --j) swap(selection[j - 1], selection[j]); ++right; continue; } if (selection[left + localCatchUp] >= arr[i]) { selection[left] = arr[i]; for (int j = left; selection[j] >= selection[j + 1]; ++j) swap(selection[j], selection[j + 1]); --left; continue; } if (i & 1) { // i -  restFirst[restFirstLen++] = arr[i]; } else { restSecond[restSecondLen++] = arr[i]; } } delete[] arr; int selectionLen = right - left - 1; //     int* copy = glue(selection + left + 1, selectionLen, nullptr, 0); //        delete[] selection; //    2 * len   selection = copy; //      ,   newGenerationSort(restFirst, restFirstLen); newGenerationSort(restSecond, restSecondLen); int* part2; int part2Len; if (selectionLen < restFirstLen) { glueDelete(selection, restFirst, restFirstLen, selection, selectionLen); // selection += restFirst selectionLen += restFirstLen; part2 = restSecond; part2Len = restSecondLen; } else { glueDelete(part2, restFirst, restFirstLen, restSecond, restSecondLen); // part2 = restFirst + restSecond part2Len = restFirstLen + restSecondLen; } glueDelete(arr, selection, selectionLen, part2, part2Len); } 

الآن اختبار الوقت

 #include <iostream> #include <ctime> #include <vector> #include <algorithm> #include "time_utilities.h" #include "sort_utilities.h" using namespace std; using namespace rela589n; void printArr(int* arr, int len) { for (int i = 0; i < len; ++i) { cout << arr[i] << " "; } cout << endl; } bool arraysEqual(int* arr1, int* arr2, int len) { for (int i = 0; i < len; ++i) { if (arr1[i] != arr2[i]) { return false; } } return true; } int* createArray(int length) { int* a1 = new int[length]; for (int i = 0; i < length; i++) { a1[i] = rand(); //a1[i] = (i + 1) % (length / 4); } return a1; } int* array_copy(int* arr, int length) { int* a2 = new int[length]; for (int i = 0; i < length; i++) { a2[i] = arr[i]; } return a2; } void tester(int tests, int length) { double t1, t2; int** arrays1 = new int* [tests]; int** arrays2 = new int* [tests]; for (int t = 0; t < tests; ++t) { //    int* arr1 = createArray(length); arrays1[t] = arr1; arrays2[t] = array_copy(arr1, length); } t1 = getCPUTime(); for (int t = 0; t < tests; ++t) { quickSort(arrays1[t], 0, length - 1); } t2 = getCPUTime(); cout << "Avg Qsort time for " << length << " elements: " << (t2 - t1) * 1000 / tests << endl; int portion = catchUp = 8; t1 = getCPUTime(); for (int t = 0; t < tests; ++t) { newGenerationSort(arrays2[t], length); } t2 = getCPUTime(); cout << "Avg newGenSort time for " << length << " elements: " << (t2 - t1) * 1000 / tests //<< " Catch up coef: "<< portion << endl; bool confirmed = true; //     for (int t = 0; t < tests; ++t) { if (!arraysEqual(arrays1[t], arrays2[t], length)) { confirmed = false; break; } } if (confirmed) { cout << "Confirmed" << endl; } else { cout << "Review your code! Something wrong..." << endl; } } int main() { srand(time(NULL)); int length; double t1, t2; cout << "size: "; cin >> length; int t; cout << "tests: "; cin >> t; tester(t, length); system("pause"); return 0; } 

 // [min, max] int random(int min, int max) { return min + rand() % ((max + 1) - min); } void quickSort(int * arr, int b, int e) { int l = b, r = e; int piv = arr[random(l, r)]; while (l <= r) { for (; arr[l] < piv; ++l); for (; arr[r] > piv; --r); if (l <= r) swap(arr[l++], arr[r--]); } if (b < r) quickSort(arr, b, r); if (e > l) quickSort(arr, l, e); } 

 #pragma once #if defined(_WIN32) #include <Windows.h> #elif defined(__unix__) || defined(__unix) || defined(unix) || (defined(__APPLE__) && defined(__MACH__)) #include <unistd.h> #include <sys/resource.h> #include <sys/times.h> #include <time.h> #else #error "Unable to define getCPUTime( ) for an unknown OS." #endif /** * Returns the amount of CPU time used by the current process, * in seconds, or -1.0 if an error occurred. */ double getCPUTime() { #if defined(_WIN32) /* Windows -------------------------------------------------- */ FILETIME createTime; FILETIME exitTime; FILETIME kernelTime; FILETIME userTime; if (GetProcessTimes(GetCurrentProcess(), &create;Time, &exit;Time, &kernel;Time, &user;Time) != -1) { SYSTEMTIME userSystemTime; if (FileTimeToSystemTime(&user;Time, &user;SystemTime) != -1) return (double)userSystemTime.wHour * 3600.0 + (double)userSystemTime.wMinute * 60.0 + (double)userSystemTime.wSecond + (double)userSystemTime.wMilliseconds / 1000.0; } #elif defined(__unix__) || defined(__unix) || defined(unix) || (defined(__APPLE__) && defined(__MACH__)) /* AIX, BSD, Cygwin, HP-UX, Linux, OSX, and Solaris --------- */ #if defined(_POSIX_TIMERS) && (_POSIX_TIMERS > 0) /* Prefer high-res POSIX timers, when available. */ { clockid_t id; struct timespec ts; #if _POSIX_CPUTIME > 0 /* Clock ids vary by OS. Query the id, if possible. */ if (clock_getcpuclockid(0, &id;) == -1) #endif #if defined(CLOCK_PROCESS_CPUTIME_ID) /* Use known clock id for AIX, Linux, or Solaris. */ id = CLOCK_PROCESS_CPUTIME_ID; #elif defined(CLOCK_VIRTUAL) /* Use known clock id for BSD or HP-UX. */ id = CLOCK_VIRTUAL; #else id = (clockid_t)-1; #endif if (id != (clockid_t)-1 && clock_gettime(id, &ts;) != -1) return (double)ts.tv_sec + (double)ts.tv_nsec / 1000000000.0; } #endif #if defined(RUSAGE_SELF) { struct rusage rusage; if (getrusage(RUSAGE_SELF, &rusage;) != -1) return (double)rusage.ru_utime.tv_sec + (double)rusage.ru_utime.tv_usec / 1000000.0; } #endif #if defined(_SC_CLK_TCK) { const double ticks = (double)sysconf(_SC_CLK_TCK); struct tms tms; if (times(&tms;) != (clock_t)-1) return (double)tms.tms_utime / ticks; } #endif #if defined(CLOCKS_PER_SEC) { clock_t cl = clock(); if (cl != (clock_t)-1) return (double)cl / (double)CLOCKS_PER_SEC; } #endif #endif return -1; /* Failed. */ } 

تم إجراء جميع الاختبارات على الجهاز بنسبة مئوية. إنتل كور i3 7100u و 8 جيجابايت من ذاكرة الوصول العشوائي

مجموعة عشوائية تماما

 a1[i] = rand(); 

صفيف مرتب جزئيًا

 a1[i] = (i + 1) % (length / 4); 

مجموعة مصنفة بالكامل

 a1[i] = (i + 1); 

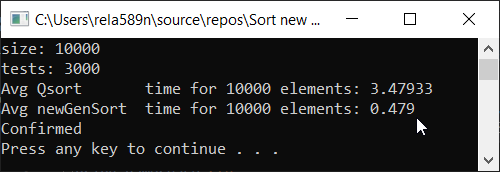
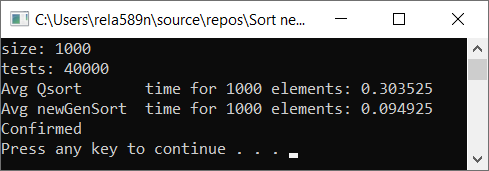
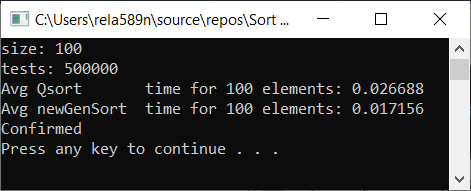
النتائج

كما ترون ، الخوارزمية تعمل وتعمل بشكل جيد. على الأقل كل ما أردناه تم تحقيقه. على حساب الاستقرار ، لست متأكدًا من أنني لم أتحقق من ذلك. يمكنك التحقق من ذلك بنفسك. ولكن من الناحية النظرية ينبغي أن يتحقق بسهولة بالغة. فقط في بعض الأماكن ، بدلاً من العلامة> ضع ≥ أو شيء ما.