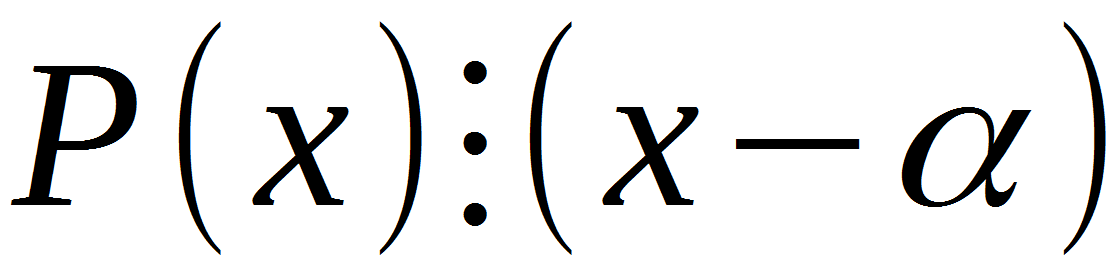
وكقاعدة عامة ، في الفيزياء وعلوم الكمبيوتر والاقتصاد ، نواجه أبسط المعادلات الخطية أو المنطقية الكسرية ، وغالبًا ما نواجه المعادلات التربيعية. وماذا عن معادلات الدرجة الثالثة والرابعة؟ إذا كنت مهتما ، فأنا أطلب قطة.
أولا ، النظر في مفهوم المعادلة من أعلى درجة. معادلة الدرجة الأعلى هي معادلة الشكل:

في هذه المقالة سأنظر في:
1. المعادلات مكعب.
2. مكعب قابل للإرجاع.
3. تطبيق مخطط هورنر ونظرية بيزوت.
4. معادلات biquadratic يمكن إرجاعها.
معادلات مكعبة
المعادلات التكعيبية هي معادلات لا تكون فيها الدرجة المجهولة معروفة بالنسبة إلى الفصل الدراسي الأول ، وتكون المعادلات التكعيبية بالشكل التالي:

يمكن حل هذه المعادلات بطرق مختلفة ، ومع ذلك ، سوف نستخدم معرفة المدرسة الأساسية وحل المعادلة المكعبة بواسطة طريقة التجميع:

في هذا المثال ، يتم استخدام طريقة التجميع ، حيث نقوم بتجميع أول عضوين وآخرين ، ونحصل على أقواس متساوية ، ومرة أخرى نجعلها ، ونحصل على معادلة بين قوسين.
يكون المنتج مساوياً للصفر ، وفقط إذا كان أحد العوامل على الأقل مساوياً للصفر ، وبناءً على هذا فإننا نعادل كل عامل (قوس) بالصفر ، والحصول على معادلة غير كاملة وخطية من الدرجة الثانية.
تجدر الإشارة أيضًا إلى أن الحد الأقصى لعدد جذور المعادلة يساوي الدرجة غير المعروفة مع المصطلح البادئ ، لذلك في المعادلة المكعبة لا يمكن أن يكون هناك أكثر من ثلاثة جذور ، في biquadratic (الدرجة الرابعة) لا يزيد عن أربعة جذور و. ر. د.
عودة المعادلات المكعبة
معادلات المكعبات المرتدة لها الشكل:

ويطلق عليهم إرجاع لأن المعاملات ستكون معكوسة. يتم حل المعادلات المماثلة أيضًا بالطرق المدرسية ، ولكن معقد بعض الشيء:

أولاً ، يتم إجراء التجميع ، ثم باستخدام صيغ الضرب المختصر ، نحلل العوامل الناتجة. مرة أخرى نحصل على قوسين متساويين ، "نخرجهما". نحصل على عاملين (الأقواس) ونحلها كمعادلتين مختلفتين.
نظرية بيزوت ومخطط هورنر
تم اكتشاف نظرية بيزوت ، على نحو مفاجئ ، من قبل إتيان بيزوت ، عالم الرياضيات الفرنسي الذي كان يهتم بشكل أساسي بالجبر. يمكن صياغة نظرية بيزوت على النحو التالي:

دعونا معرفة ذلك. P (x) هو أي متعدد الحدود في x ، (x - a) هي ذات الحدين الذي يمثل أحد الجذور الكاملة للمعادلة التي نجدها بين مقسومات المصطلح الحر.
ثلاث نقاط ، هذا هو عامل يشير إلى أن تعبير واحد مقسوم على آخر. يستنتج من ذلك أنه بعد العثور على جذر واحد على الأقل من المعادلة ، يمكننا تطبيق هذه النظرية عليها. ولكن لماذا هذه النظرية مطلوبة ، ما هو تأثيرها؟ تعتبر نظرية Bezout أداة عالمية إذا كنت ترغب في خفض درجة كثير الحدود. على سبيل المثال ، بمساعدتها ، يمكن تحويل المعادلة المكعبة إلى مربع ، biquadratic ، مكعب ، الخ.
لكن هذا شيء واحد يجب أن نفهمه ، لكن كيف نقسمه؟ بالطبع ، يمكنك تقسيمها في عمود ، لكن هذه الطريقة غير متاحة للجميع ، واحتمال ارتكاب خطأ كبير للغاية. لذلك ، هناك طريقة أخرى ، وهذا هو مخطط هورنر. سأشرح عملها بمثال. نفترض:

وهكذا ، لقد حصلنا على كثير الحدود ، وربما وجدنا واحدة من الجذور مقدما. نرسم الآن صفيحة صغيرة من 6 أعمدة وصفين ، في كل عمود من الصف الأول (باستثناء الأول) ، نقدم معاملات المعادلة. وفي العمود الأول من الصف 2 ، نضيف قيمة (الجذر الموجود). ثم المعامل الأول ، في حالتنا 5 ، نحن نسقط فقط. يتم حساب قيم الأعمدة التالية على النحو التالي:

(الصورة مستعارة
هنا )
بعد ذلك ، نفعل نفس الشيء مع بقية الأعمدة. ستكون قيمة العمود الأخير (صفين) هي الباقي من القسمة ، في حالتنا 0 ، إذا حصلت على رقم بخلاف 0 ، فأنت بحاجة إلى اختيار طريقة مختلفة. مثال لمعادلة مكعب:

معادلات Biquadratic المرتجعة
نظرنا أيضًا في معادلات المكعبات الموضحة أعلاه ، والآن نقوم بتحليل المعادلات biquadratic. وجهة نظرهم العامة:

على عكس معادلة العائد المكعب ، لا يوجد لدى كل شخص زوج ثنائي الاتجاه فيما يتعلق بالمعاملات ، لكنهما متشابهان للغاية. هذه هي الخوارزمية لحل هذه المعادلات:

كما ترون ، حل هذه المعادلات ليس بالأمر السهل. لكنني سأصدر هذه القضية على أي حال. يبدأ الحل بقسمة المعادلة بأكملها على x ^ 2. بعد ذلك ، نحن المجموعة ، هنا قدمت تحديداً خطًا إضافيًا للوضوح. بعد ذلك ، نقوم بالخدعة ، ونحن ندخل في الشريحة الأولى 2 ، التي نضيفها أولاً ، ثم نطرحها ، فلن يتغير المبلغ على أي حال ، لكن الآن يمكننا طي هذه الشريحة في مربع المجموع.
نزيل -2 من الأقواس ، ونضربها أولاً بـ a ، وبعد ذلك نقدم متغيرًا جديدًا ، ونحصل على المعادلة التربيعية.
الآن دعنا ننتقل إلى مثال:

الجزء الرئيسي ، كما هو الحال في الخوارزمية المعممة ، مقسوم على x ^ 2 ، مجمعة ، انهارت في مربع كامل ، نحن نؤدي الاستبدال المتغير ونحل المعادلة التربيعية. بعد ذلك ، نقوم باستبدال الجذور التي تم الحصول عليها ، ونحل معادلتين أخريين (مضروبة في x).
مجال التطبيق
بسبب ضخامتها وخصائصها ، نادراً ما تجد معادلات الدرجات العليا تطبيقها. ومع ذلك ، لا تزال هناك أمثلة ، معادلة بواسون للعمليات الأدبية في الفيزياء.
استنتاج
في هذه المقالة ، فكرت فقط في المعادلات التكعيبية والتقليدية. ومع ذلك ، يمكن استخدام نظرية Bezout المدروسة (ومخطط Horner) لحل معادلات 5 و 6 و 7 ودرجات أخرى ، على الرغم من أن تطبيقها محدود.