في Serokell ، نحن لا نشارك فقط في مشاريع تجارية ، ولكننا نسعى أيضًا لتغيير العالم نحو الأفضل. على سبيل المثال ، نحن نعمل على تحسين الأداة الرئيسية لجميع Haskelists - Glasgow Haskell Compiler (GHC). ركزنا على توسيع نظام الكتابة تحت تأثير عمل ريتشارد أيزنبرغ ، "الأنواع التابعة في هاسكل: النظرية والتطبيق" .

في مدونتنا ، تحدث فلاديسلاف بالفعل عن سبب افتقار هاسكل إلى الأنواع التابعة وكيف نخطط لإضافتها. قررنا ترجمة هذا المنشور إلى الروسية حتى يتمكن أكبر عدد ممكن من المطورين من استخدام الأنواع التابعة وتقديم مساهمة إضافية في تطوير Haskell كلغة.

الوضع الحالي

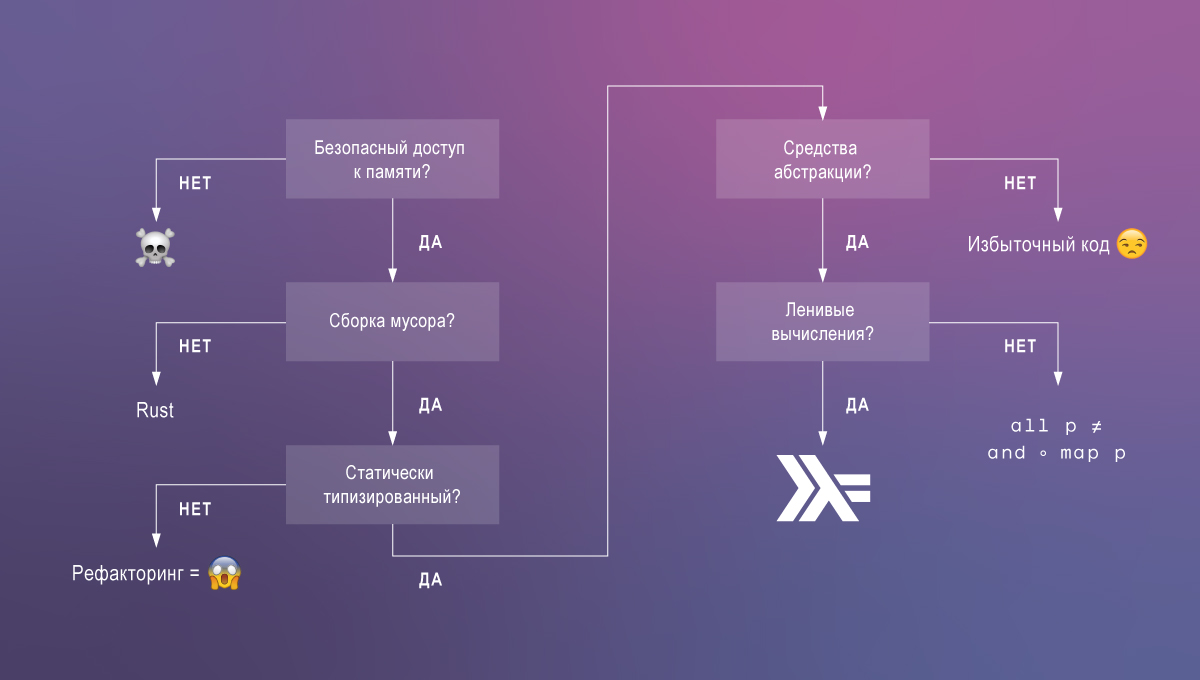
الأنواع التابعة هي أكثر ما أفتقده في هاسكل. لنناقش السبب. من الكود الذي نريده:

• الأداء ، أي سرعة التنفيذ وانخفاض استهلاك الذاكرة ؛
• الصيانة وسهولة الفهم ؛
• صحة مضمونة من طريقة تجميعها.

من خلال التقنيات الحالية ، نادراً ما يكون من الممكن تحقيق الخصائص الثلاث ، ولكن مع دعم الأنواع التي تعتمد على Haskell ، يتم تبسيط المهمة.

هاسكل قياسي: بيئة العمل + الأداء

يستند Haskell إلى نظام بسيط: حساب التفاضل والتكامل متعدد الأشكال lambda مع حسابات كسول ، وأنواع البيانات الجبرية ، وفئات الكتابة. هذا المزيج من الميزات اللغوية هو الذي يتيح لنا كتابة رمز أنيق ومدعوم وفي نفس الوقت إنتاجي. لإثبات هذا الادعاء ، قمنا بمقارنة باختصار Haskell مع لغات أكثر شعبية.

اللغات ذات الوصول غير الآمن للذاكرة ، مثل C ، تؤدي إلى أخطر الأخطاء ونقاط الضعف (على سبيل المثال ، تجاوز سعة المخزن المؤقت ، تسرب الذاكرة). في بعض الأحيان تكون هناك حاجة إلى مثل هذه اللغات ، ولكن في أغلب الأحيان يكون استخدامها مجرد فكرة.

تشكل لغات الوصول إلى الذاكرة الآمنة مجموعتين: تلك التي تعتمد على أداة تجميع مجمعي البيانات المهملة و Rust. يبدو Rust أنه فريد من نوعه في توفير وصول آمن إلى الذاكرة دون تجميع البيانات المهملة . لم يعد هناك أيضًا إعصار معتمد ولغات بحث أخرى في هذه المجموعة. ولكن على عكسهم ، روست في طريقه إلى الشعبية. العيب هو أنه على الرغم من الأمان ، فإن إدارة ذاكرة Rust غير تافهة ودليلة. في التطبيقات التي يمكنها استخدام أداة تجميع مجمعي البيانات المهملة ، من الأفضل قضاء وقت للمطورين في مهام أخرى.

هناك لغات متبقية مع جامعي القمامة ، والتي سنقسمها إلى فئتين على أساس نظام الكتابة.

لا تقدم اللغات المكتوبة ديناميكيًا (أو بالأحرى أحادية النمط ) ، مثل JavaScript أو Clojure ، تحليلًا ثابتًا ، وبالتالي لا يمكنها توفير نفس مستوى الثقة في صحة الكود (ولا ، الاختبارات لا يمكن أن تحل محل الأنواع - فأنت بحاجة إلى كليهما) !).

غالبًا ما يكون للغات المطبوعة بشكل ثابت مثل Java أو Go نظام كتابة محدود للغاية. هذا يفرض المبرمجين لكتابة التعليمات البرمجية الزائدة ووضع ميزات لغة غير آمنة. على سبيل المثال ، يؤدي الافتقار إلى الأنواع العامة في Go إلى فرض استخدام الواجهة {} وتتبع أنواع وقت التشغيل . لا يوجد أيضًا فصل بين العمليات الحسابية ذات الآثار الجانبية (المدخلات والمخرجات) والحسابات البحتة.

أخيرًا ، من بين اللغات التي تتمتع بالوصول الآمن للذاكرة ، وجامع القمامة ، ونظام الكتابة القوي ، تميز Haskell عن الكسل. الحوسبة الكسولة مفيدة للغاية لكتابة التعليمات البرمجية المركبة القابلة للتكوين. أنها تجعل من الممكن أن تتحلل إلى تعريفات مساعدة أي أجزاء من التعبيرات ، بما في ذلك المنشآت التي تحدد تدفق التحكم.

تبدو هاسكل لغة مثالية تقريبًا إلى أن تدرك مدى بعيدًا عن إطلاق إمكاناتها الكاملة من حيث التحقق الثابت مقارنة بأدوات إثبات النظرية مثل Agda .

كمثال بسيط على عدم وجود نظام نوع Haskell بما يكفي ، فكر في عامل فهرسة القائمة من Prelude (أو فهرسة صفيف من حزمة primitive ):

 (!!) :: [a] -> Int -> a indexArray :: Array a -> Int -> a 

لا يوجد في هذه التواقيع النوعية ما يعكس اشتراط أن يكون الفهرس غير سالب وأقل من طول المجموعة. بالنسبة للبرامج ذات متطلبات الموثوقية العالية ، هذا أمر غير مقبول.

Agda: بيئة العمل + صحة

أدوات إثبات النظريات (على سبيل المثال ، Coq ) هي أدوات برمجية تسمح باستخدام الكمبيوتر لتطوير أدلة رسمية للنظريات الرياضية. بالنسبة لعالم الرياضيات ، فإن استخدام هذه الأدوات يشبه كتابة الأدلة على الورق. الفرق في الدقة غير المسبوقة التي يتطلبها الكمبيوتر لإثبات صحة هذه الأدلة.

بالنسبة للمبرمج ، فإن وسائل إثبات النظريات لا تختلف كثيراً عن المترجم الخاص بلغة البرمجة الباطنية بنظام كتابة لا يصدق (وربما بيئة تطوير متكاملة) ، ومتوسط ​​(أو حتى غائب) لكل شيء آخر. إن وسيلة إثبات النظريات هي ، في الواقع ، لغات البرمجة ، التي قضى مؤلفوها كل وقتهم في تطوير نظام للكتابة ونسوا أنه لا يزال يتعين تشغيل البرامج.

الحلم الذي يعتز به مطورو البرمجيات الذين تم التحقق منهم هو وسيلة لإثبات النظريات ، والتي ستكون لغة برمجة جيدة مع مولد رمز عالي الجودة ووقت تشغيل. في هذا الاتجاه ، بما في ذلك المبدعين من إدريس جربت. لكن هذه لغة ذات حسابات صارمة (حيوية) ، وتنفيذها في الوقت الحالي غير مستقر.

من بين جميع وسائل إثبات النظريات ، فإن أغدا هاسكيليستس هي الأكثر إعجابًا. من نواح كثيرة ، يشبه Haskell ، ولكن مع نظام الكتابة أكثر قوة. نحن في Serokell نستخدمها لإثبات الخصائص المختلفة لبرامجنا. كتبت زميلتي دانيا روغوزين سلسلة من المقالات حول هذا الموضوع.

فيما يلي نوع وظيفة بحث يشبه مشغل Haskell (!!) :

 lookup : ∀ (xs : List A) → Fin (length xs) → A 

المعلمة الأولى هنا هي من النوع List A ، الذي يتوافق مع [a] في هاسكل. ومع ذلك ، فإننا نعطيها الاسم xs للإشارة إليها للفترة المتبقية من توقيع الكتابة. في Haskell ، يمكننا الوصول إلى وسيطات الوظيفة فقط في نص الدالة على مستوى المصطلح:

 (!!) :: [a] -> Int -> a --   xs  (!!) = \xs i -> ... --   xs  

ولكن في Agda ، يمكننا الإشارة إلى قيمة xs هذه على مستوى الكتابة ، وهو ما نفعله في معلمة lookup الثانية ، Fin (length xs) . تسمى الدالة التي تشير إلى المعلمة الخاصة بها في مستوى الكتابة دالة تابعة وهي مثال للأنواع التابعة.

المعلمة الثانية في lookup من النوع Fin n لـ n ~ length xs . تتطابق قيمة النوع Fin n مع رقم في النطاق [0, n) ، لذلك Fin (length xs) هو رقم غير سالب أقل من طول قائمة الإدخال. هذا هو بالضبط ما نحتاجه لتقديم فهرس صالح لعنصر قائمة. تحدث تقريبًا ، lookup ["x","y","z"] 2 فحص النوع ، ولكن lookup ["x","y","z"] 42 سيفشل.

عندما يتعلق الأمر بتشغيل برامج Agda ، يمكننا تجميعها في Haskell باستخدام خلفية MAlonzo. لكن أداء الكود الذي تم إنشاؤه سيكون غير مرضٍ. هذا ليس خطأ MAlonzo: يجب عليه إدراج العديد من unsafeCoerce بحيث unsafeCoerce GHC الكود الذي تم التحقق منه بالفعل بواسطة Agda. لكن نفس unsafeCoerce تقلل من الأداء (بعد مناقشة هذه المقالة ، اتضح أن مشاكل الأداء قد تكون ناجمة عن أسباب أخرى - ملاحظة المؤلف) .

هذا يضعنا في موقف صعب: يجب علينا استخدام Agda للنمذجة والتحقق الرسمي ، ثم إعادة تنفيذ نفس الوظيفة على Haskell. من خلال تنظيم سير العمل هذا ، تعمل شفرة Agda كمواصفات يتم التحقق منها بواسطة الكمبيوتر. هذا أفضل من المواصفات في اللغة الطبيعية ، لكنه بعيد عن المثالية. الهدف هو أنه إذا تم تجميع الشفرة ، فستعمل وفقًا للمواصفات.

هاسكل مع ملحقات: تصحيح + الأداء

تهدف ضمانات ثابتة للغات مع أنواع تابعة ، GHC قطعت شوطا طويلا. تمت إضافة ملحقات إليها لزيادة التعبير عن نظام الكتابة. لقد بدأت باستخدام Haskell عندما كان GHC 7.4 هو أحدث إصدار من المترجم. وحتى مع ذلك ، كانت تحتوي على الامتدادات الرئيسية للبرمجة المتقدمة على مستوى النوع: RankNTypes و PolyKinds و PolyKinds و PolyKinds و PolyKinds .

ومع ذلك ، لا يوجد حتى الآن أنواع مستقلة كاملة في Haskell: لا توجد وظائف تابعة (أنواع)) ولا أزواج تابعة (أنواع)). من ناحية أخرى ، على الأقل لدينا ترميز لهم!

الممارسات الحالية هي كما يلي:

• تشفير وظائف مستوى الكتابة كعائلات من النوع الخاص ،
• استخدام الوظيفية لتمكين الوظائف غير المشبعة ،
• سد الفجوة بين المصطلحات والأنواع باستخدام أنواع واحدة.

يؤدي هذا إلى قدر كبير من الشفرة الزائدة عن الحاجة ، لكن مكتبة singletons بأتمتة singletons من خلال Template Haskell.

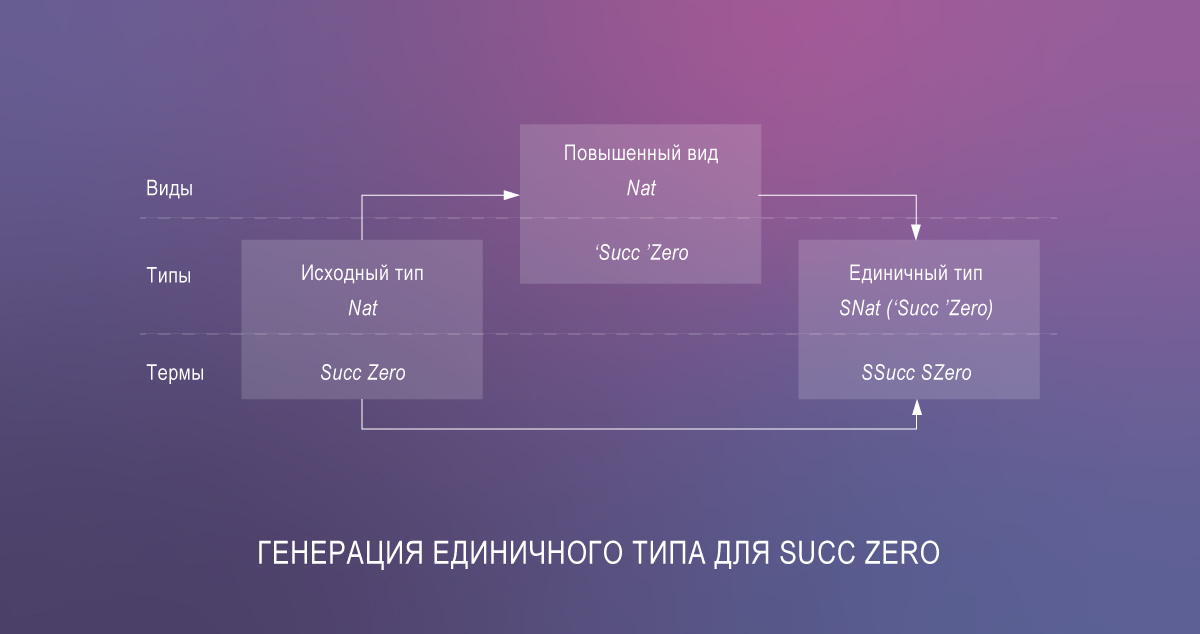
لذلك يمكن للأكثر جرأة وحاسما رمز الأنواع المعتمدة في هاسكل الآن. كتوضيح ، هنا هو تطبيق وظيفة lookup مماثلة للمتغير على Agda:

 {-# OPTIONS -Wall -Wno-unticked-promoted-constructors -Wno-missing-signatures #-} {-# LANGUAGE LambdaCase, DataKinds, PolyKinds, TypeFamilies, GADTs, ScopedTypeVariables, EmptyCase, UndecidableInstances, TypeSynonymInstances, FlexibleInstances, TypeApplications, TemplateHaskell #-} module ListLookup where import Data.Singletons.TH import Data.Singletons.Prelude singletons [d| data N = Z | SN len :: [a] -> N len [] = Z len (_:xs) = S (len xs) |] data Fin n where FZ :: Fin (S n) FS :: Fin n -> Fin (S n) lookupS :: SingKind a => SList (xs :: [a]) -> Fin (Len xs) -> Demote a lookupS SNil = \case{} lookupS (SCons x xs) = \case FZ -> fromSing x FS i' -> lookupS xs i' 

وهنا جلسة GHCi تُظهر أن عمليات البحث ترفض بالفعل الفهارس كبيرة جدًا:

 GHCi, version 8.6.2: http://www.haskell.org/ghc/ :? for help [1 of 1] Compiling ListLookup ( ListLookup.hs, interpreted ) Ok, one module loaded. *ListLookup> :set -XTypeApplications -XDataKinds *ListLookup> lookupS (sing @["x", "y", "z"]) FZ "x" *ListLookup> lookupS (sing @["x", "y", "z"]) (FS FZ) "y" *ListLookup> lookupS (sing @["x", "y", "z"]) (FS (FS FZ)) "z" *ListLookup> lookupS (sing @["x", "y", "z"]) (FS (FS (FS FZ))) <interactive>:5:34: error: • Couldn't match type ''S n0' with ''Z' Expected type: Fin (Len '["x", "y", "z"]) Actual type: Fin ('S ('S ('S ('S n0)))) • In the second argument of 'lookupS', namely '(FS (FS (FS FZ)))' In the expression: lookupS (sing @["x", "y", "z"]) (FS (FS (FS FZ))) In an equation for 'it': it = lookupS (sing @["x", "y", "z"]) (FS (FS (FS FZ))) 

يوضح هذا المثال أن الجدوى لا تعني العملية. أنا سعيد لأن لدى هاسكل قدرات لغوية لتنفيذ lookupS ، لكن في نفس الوقت أشعر بالقلق إزاء التعقيد غير الضروري الذي ينشأ. خارج المشروعات البحثية ، لا أوصي بهذا النمط من التعليمات البرمجية.

في هذه الحالة بالذات ، يمكن أن نحقق نفس النتيجة بتقليل التعقيد باستخدام متجهات مفهرسة الطول. ومع ذلك ، فإن ترجمة الشفرة المباشرة من Agda تكشف بشكل أفضل عن المشكلات التي يجب أن تواجهها في ظروف أخرى.

هؤلاء بعض منهم:

• تختلف علاقة الكتابة a :: t وعلاقة الوجهة للنموذج t :: k . 5 :: Integer صحيح من حيث ، ولكن ليس في الأنواع. "hi" :: Symbol صحيح في الأنواع ، لكن ليس من الناحية. هذا يتطلب Demote نوع Demote لتعيين أنواع Demote وأنواعها.
• تستخدم المكتبة القياسية Int لفهارس القائمة (وتستخدم singletons Nat في التعاريف المرتفعة). Int و Nat أنواع غير حثي. على الرغم من كونها أكثر كفاءة من الترميز الأحادي للأرقام الطبيعية ، إلا أنها لا تعمل بشكل جيد مع التعريفات الاستقرائية مثل Fin أو lookupS . وبسبب هذا ، فإننا نعيد تحديد length len .
• ليس لدى Haskell آليات مدمجة لرفع الوظائف إلى مستوى الأنواع. singletons كعائلات من النوع الخاص وتطبق وظائف للتحايل على عدم الاستخدام الجزئي لعائلات النوع. هذا الترميز معقد. بالإضافة إلى ذلك ، كان علينا أن نضع تعريف len في اقتباس Template Haskell حتى يولد singletons نظيره على مستوى النوع ، Len .
• لا توجد وظائف تابعة مدمجة. على المرء استخدام أنواع الوحدات لسد الفجوة بين المصطلحات والأنواع. بدلاً من القائمة المعتادة ، نقوم بتمرير SList إلى مدخلات البحث. لذلك ، يجب أن نضع في الاعتبار العديد من التعاريف للقوائم في وقت واحد. كما أنه يؤدي إلى النفقات العامة أثناء تنفيذ البرنامج. تنشأ بسبب التحويل بين القيم العادية وقيم أنواع الوحدات ( toSing ، fromSing ) وبسبب نقل إجراء التحويل (تقييد SingKind ).

الإزعاج هو المشكلة الأقل. والأسوأ من ذلك ، أن ميزات اللغة هذه غير موثوقة. على سبيل المثال ، أبلغت عن المشكلة رقم 12564 في عام 2016 ، وهناك أيضًا رقم 12088 في نفس العام. تعيق كلتا المشكلتين تنفيذ برامج أكثر تقدمًا من أمثلة من الكتب المدرسية (مثل قوائم الفهرسة). لا تزال أخطاء نظام GHC هذه غير ثابتة ، والسبب ، كما يبدو لي ، هو أن المطورين لا يملكون وقتًا كافيًا. عدد الأشخاص الذين يعملون بنشاط على GHC صغير بشكل مدهش ، لذلك لا تتفادى بعض الأشياء.

ملخص

ذكرت في وقت سابق أننا نريد الخصائص الثلاثة من الكود ، لذلك يوجد هنا جدول يوضح الحالة الراهنة:

مستقبل مشرق

من بين الخيارات الثلاثة المتاحة ، لكل منها عيوبه. ومع ذلك ، يمكننا إصلاحها:

• استخدم Haskell القياسي وأضف أنواعًا مستقلة مباشرةً بدلاً من الترميز غير المناسب عبر singletons . (قال أسهل من القيام به.)
• خذ Agda وتنفيذ منشئ رمز فعال و RTS لذلك. (قال أسهل من القيام به.)
• خذ Haskell مع ملحقات ، وإصلاح الخلل والاستمرار في إضافة ملحقات جديدة لتبسيط ترميز الأنواع التابعة. (قال أسهل من القيام به.)

والخبر السار هو أن الخيارات الثلاثة تتلاقى عند نقطة واحدة (بمعنى ما). تخيل أصغر امتداد لـ Haskell القياسي الذي يضيف أنواعًا تابعة ، وبالتالي ، يسمح لك بضمان صحة الكود بالطريقة المكتوبة به. يمكن تجميع كود unsafeCoerce (نقله) إلى هذه اللغة دون unsafeCoerce . و Haskell مع الامتدادات ، إلى حد ما ، هو نموذج غير مكتمل لهذه اللغة. يجب تحسين شيء ما ، ويجب إزالة شيء ما ، ولكن في النهاية ، سنحقق النتيجة المرجوة.

التخلص من singletons

مؤشر جيد للتقدم هو تبسيط مكتبة singletons . نظرًا لأنه يتم تنفيذ أنواع تابعة في Haskell ، لم تعد هناك حاجة إلى حلول خاصة ومعالجة خاصة للحالات singletons . في النهاية ، ستختفي الحاجة إلى هذه الحزمة تمامًا. على سبيل المثال ، في عام 2016 ، باستخدام ملحق -XTypeInType قمت بإزالة KProxy من SingKind و SomeSing . تم إجراء هذا التغيير من خلال اتحاد الأنواع والأنواع. قارن بين التعريفات القديمة والجديدة:

 class (kparam ~ 'KProxy) => SingKind (kparam :: KProxy k) where type DemoteRep kparam :: * fromSing :: SingKind (a :: k) -> DemoteRep kparam toSing :: DemoteRep kparam -> SomeSing kparam type Demote (a :: k) = DemoteRep ('KProxy :: KProxy k) data SomeSing (kproxy :: KProxy k) where SomeSing :: Sing (a :: k) -> SomeSing ('KProxy :: KProxy k) 

في التعريفات القديمة ، يحدث k بشكل حصري في مواضع العرض ، إلى يمين التعليقات التوضيحية للنموذج t :: k . نحن نستخدم kparam :: KProxy k لنقل k إلى الأنواع.

 class SingKind k where type DemoteRep k :: * fromSing :: SingKind (a :: k) -> DemoteRep k toSing :: DemoteRep k -> SomeSing k type Demote (a :: k) = DemoteRep k data SomeSing k where SomeSing :: Sing (a :: k) -> SomeSing k 

في التعاريف الجديدة ، تنتقل k بحرية بين عرض ونوع المواضع ، لذلك لم نعد بحاجة إلى KProxy . والسبب هو أنه ، بدءًا من GHC 8.0 ، تندرج الأنواع والأنواع في نفس الفئة النحوية.

هناك ثلاثة عوالم منفصلة تمامًا في Haskell القياسية: المصطلحات ، الأنواع ، وجهات النظر. إذا نظرت إلى الكود المصدري لـ GHC 7.10 ، يمكنك رؤية محلل منفصل لوجهات النظر وفحص منفصل. لم يعد لديهم GHC 8.0: يعد المحلل اللغوي والتحقق من صحة الأنواع وطرق العرض شائعًا.

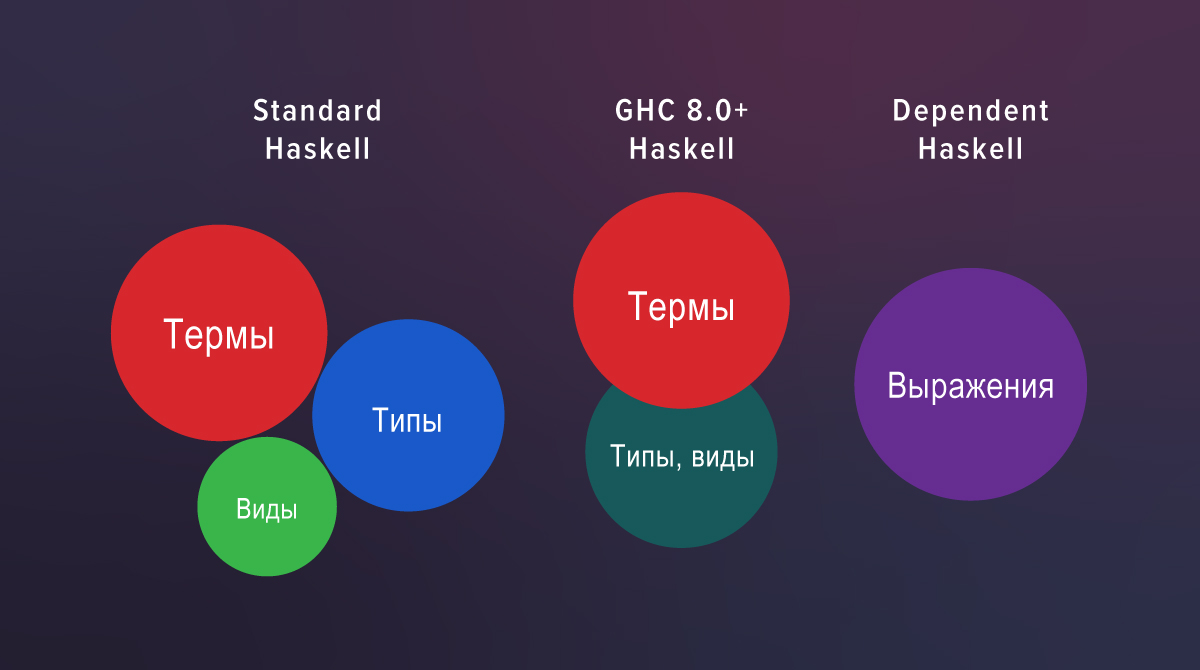
في Haskell مع الإضافات ، يعد العرض مجرد الدور الذي يلعبه النوع:

 f :: T z -> ... -- 'z'   g :: T (a :: z) -> ... -- 'z'   h :: T z -> T (a :: z) -> ... -- 'z'   ,   

في GHC 8.0-8.4 ، لا تزال هناك بعض الاختلافات بين تحليل الاسم في الأنواع والأنواع. لكنني قمت StarIsType إلى GHC 8.6: قمت بإنشاء ملحق TypeInType وأدخلت وظيفة PolyKinds في PolyKinds . الخلافات المتبقية التي وجهتها إلى GHC 8.8 ، وتم إزالتها تمامًا في GHC 8.10

ما هي الخطوة التالية؟ دعونا نلقي نظرة على SingKind في أحدث إصدار من singletons :

 class SingKind k where type Demote k = (r :: Type) | r -> k fromSing :: Sing (a :: k) -> Demote k toSing :: Demote k -> SomeSing k 

Demote نوع Demote ضرورية لحساب التباينات بين علاقة الكتابة a :: t وعلاقة الوجهة للنموذج t :: k . في معظم الأحيان (لأنواع البيانات الجبرية) ، يعد Demote بمثابة مخطط Demote الهوية:

• type Demote Bool = Bool
• type Demote [a] = [Demote a]
• type Demote (Either ab) = Either (Demote a) (Demote b)

لذلك ، Demote (Either [Bool] Bool) = Either [Bool] Bool . هذه الملاحظة تطالبنا بالقيام بالتبسيط التالي:

 class SingKind k where fromSing :: Sing (a :: k) -> k toSing :: k -> SomeSing k 

ليست هناك حاجة Demote ! وفي الواقع ، قد ينجح هذا مع كل من Either [Bool] Bool وأنواع البيانات الجبرية الأخرى. في الممارسة العملية ، ومع ذلك ، فإننا نتعامل مع أنواع البيانات غير الجبرية: Integer, Natural ، Char ، Text ، وهلم جرا. إذا تم استخدامها كنوع ، فهي غير مأهولة بالسكان: 1 :: Natural صحيح على مستوى المصطلحات ، ولكن ليس على مستوى الأنواع. لهذا السبب ، نحن نتعامل مع مثل هذه التعريفات:

 type Demote Nat = Natural type Demote Symbol = Text 

الحل لهذه المشكلة هو رفع أنواع بدائية. على سبيل المثال ، Text تعريف Text مثل هذا:

 -- | A space efficient, packed, unboxed Unicode text type. data Text = Text {-# UNPACK #-} !Array -- payload (Word16 elements) {-# UNPACK #-} !Int -- offset (units of Word16, not Char) {-# UNPACK #-} !Int -- length (units of Word16, not Char) data Array = Array ByteArray# data Int = I# Int# 

إذا قمنا برفع ByteArray# و Int# بشكل صحيح إلى مستوى الأنواع ، فيمكننا استخدام Text بدلاً من Symbol . من خلال القيام بالشيء نفسه مع Natural وربما بضعة أنواع أخرى ، يمكنك التخلص من Demote ، أليس كذلك؟

للأسف ، ليس كذلك. في ما سبق ، غضت الطرف عن أهم أنواع البيانات: الوظائف. لديهم أيضًا مثيل Demote خاص:

 type Demote (k1 ~> k2) = Demote k1 -> Demote k2 type a ~> b = TyFun ab -> Type data TyFun :: Type -> Type -> Type 

~> هذا هو النوع الذي يتم به ترميز وظائف مستوى الكتابة في أحرف مفردة بناءً على عائلات من النوع الخاص والتشغيل.

في البداية ، قد يبدو الجمع بين ~> و -> فكرة جيدة ، لأن كلاهما يعني النوع (النوع) من الوظيفة. المشكلة هي أن -> في موضع الكتابة و -> في موضع العرض تعني أشياء مختلفة. على مستوى المدى ، تكون جميع الوظائف من a إلى b من النوع a -> b . على مستوى الكتابة ، يكون المُنشئون فقط من a إلى b هم من النوع a -> b ، لكنهم ليسوا مرادفات للأنواع وليسوا عائلات. من أجل استنتاج الأنواع ، يفترض GHC أن f ~ g و a ~ b يتبعان fa ~ gb ، وهذا صحيح بالنسبة للمُنشئين ، ولكن ليس للوظائف - ولهذا السبب يوجد قيود.

لذلك ، من أجل رفع الوظائف إلى مستوى الأنواع ، ولكن للحفاظ على استنتاج الكتابة ، سيتعين علينا نقل المنشئات إلى نوع منفصل. نسميها a :-> b ، لأنه سيكون صحيحًا حقًا أن f ~ g و a ~ b يتبع من fa ~ gb . ستظل الوظائف الأخرى من النوع a -> b . على سبيل المثال ، Just :: a :-> Maybe a ، لكن في الوقت نفسه isJust :: Maybe a -> Bool .

عند الانتهاء من Demote ، فإن الخطوة الأخيرة هي التخلص من Sing نفسه. للقيام بذلك ، نحتاج إلى مقياس جديد ، هجين بين forall و -> . دعونا نلقي نظرة فاحصة على وظيفة isJust:

 isJust :: forall a. Maybe a -> Bool isJust = \x -> case x of Nothing -> False Just _ -> True 

يتم isJust وظيفة isJust بالنوع a ثم بالقيمة x :: Maybe a . هذه المعلمتين لها خصائص مختلفة:

• الوضوح. في isJust (Just "hello") ، نعبر x = Just "hello" بشكل صريح ، و a = String يتم إخراجها ضمنيًا بواسطة المحول البرمجي. في Haskell الحديثة ، يمكننا أيضًا فرض التمرير الصريح لكلتا المعلمتين: isJust @String (Just "hello") .
• أهميتها. سيتم أيضًا نقل القيمة التي تم تمريرها إلى الإدخال إلى isJust في التعليمات البرمجية أثناء تنفيذ البرنامج: فنحن isJust مع case للتحقق من أنه Nothing أو Just . لذلك ، تعتبر القيمة ذات صلة. ولكن يتم مسح نوعه ولا يمكن مقارنته بالنمط: تتعامل الوظيفة مع Maybe Int ، و Maybe String ، و Maybe Bool ، إلخ. لذلك ، فهو يعتبر غير ذي صلة. وتسمى هذه الخاصية أيضا parametricity.
• الاعتماد. في forall a. t forall a. t ، قد يشير النوع t إلى a ، وبالتالي ، يعتمد على المعبر الخاص a . على سبيل المثال ، isJust @String من النوع Maybe String -> Bool ، و isJust @Int من النوع Maybe Int -> Bool . وهذا يعني أن forall هو الكمي forall . لاحظ الفرق مع معلمة القيمة: لا يهم ما إذا كنا نسميها isJust (Just …) isJust Nothing أو isJust (Just …) ، نوع النتيجة هو دائمًا Bool . لذلك ، -> هو الكمي المستقل.

لإخراج Sing ، نحتاج إلى أداة قياس كمية صريحة وذات صلة ، مثل a -> b ، وفي الوقت نفسه تعتمد ، مثل forall (a :: k). t forall (a :: k). t . تدل على أنها foreach (a :: k) -> t . لإخراج SingI ، نقدم أيضًا SingI تابعًا ذي صلة ضمنيًا ، foreach (a :: k). t foreach (a :: k). t . نتيجة لذلك ، لن تكون هناك حاجة إلى مفردات لأننا أضفنا للتو وظائف تابعة إلى اللغة.

نظرة سريعة على هاسكل مع أنواع تابعة

مع صعود الوظائف إلى مستوى الأنواع lookupS ، يمكننا إعادة كتابة lookupS النحو التالي:

 data N = Z | SN len :: [a] -> N len [] = Z len (_:xs) = S (len xs) data Fin n where FZ :: Fin (S n) FS :: Fin n -> Fin (S n) lookupS :: foreach (xs :: [a]) -> Fin (len xs) -> a lookupS [] = \case{} lookupS (x:xs) = \case FZ -> x FS i' -> lookupS xs i' 

باختصار ، لم يفعل الكود ، لكن singletons جيدة في إخفاء الشفرة الزائدة عن الحاجة. ومع ذلك ، فإن الكود الجديد أبسط بكثير: لم يعد هناك SingKind ، SList ، SNil ، SCons ، fromSing ، fromSing . لا يوجد استخدام لـ TemplateHaskell ، حيث يمكننا الآن استدعاء الدالة len مباشرةً بدلاً من إنشاء عائلة نوع Len . سيكون الأداء أيضًا أفضل ، حيث أنك لم تعد بحاجة إلى التحويل من fromSing .

لا يزال يتعين علينا إعادة تعريف length أنه len لإرجاع N معرف تعريفياً بدلاً من Int . ربما لا ينبغي اعتبار هذه المشكلة في إطار إضافة أنواع تابعة إلى Haskell ، لأن Agda يستخدم أيضًا N محدد تعريفًا في وظيفة lookup .

في بعض الجوانب ، تعد Haskell ذات الأنواع التابعة أبسط من Haskell القياسية. لا يزال ، في المصطلحات ، يتم دمج الأنواع والأنواع في لغة واحدة موحدة. يمكنني بسهولة تخيل كتابة التعليمات البرمجية في هذا النمط في مشروع تجاري لإثبات صحة المكونات الأساسية للتطبيقات رسميًا. يمكن أن توفر العديد من مكتبات Haskell واجهات أكثر أمانًا دون تعقيد singletons .

هذا لن يكون سهلا. نواجه العديد من المشكلات الهندسية التي تؤثر على جميع مكونات GHC: المحلل اللغوي ، تحليل الاسم ، فحص النوع ، وحتى اللغة الأساسية. كل شيء سوف تحتاج إلى تعديل ، أو حتى إعادة تصميمها بالكامل.

قاموس