شجرة القطاع: سريعة وسهلة

عشية الإطلاق التالي لدورة "الخوارزميات للمطورين" ، أجرينا درسًا مفتوحًا . لقد تحدثوا عن الفكرة المعروفة لشجرة المقاطع ، وناقشوا كيفية بنائها ، وتحديثها ، وسرعان ما حساب O(log n) مجموع أرقام أي شريحة من مجموعة معينة. الخوارزمية بسيطة جدًا واقتصادية: تحتاج إلى ذاكرة O(n) . لتوحيد المواد ، حلوا مشكلة olympiad.

---

تم إجراء الندوة عبر الويب بواسطة مبرمج ومعلم من ذوي الخبرة ، بالإضافة إلى رئيس الدورة "خوارزميات للمطورين" Evgeny Volosatov .

القول

شجرة المقاطع عبارة عن بنية بيانات تتيح البحث السريع الخوارزمي واللوغاريتمي السريع لمجموع عناصر الصفيف في مقطع معين.

على سبيل المثال ، تخيل أنك بحاجة إلى العثور على مجموع الأرقام التالية:



في هذه الحالة ، لا نحتاج فقط إلى حساب مجموع أرقام التسلسل المحدد (مجموع عناصر صفيف معين) ، ولكن في أسرع وقت ممكن للعثور على مجموع أي تسلسل من هذه الأرقام . بمعنى أنه يمكننا أن نسأل بعض الفاصل (المقطع) ونقدم الإجابة في أسرع وقت ممكن ، ما هو مجموع الأرقام من هذا الفاصل الزمني:



ماذا يعني الصيام؟ هذا يعني أسرع مما لو كنا ببساطة أضفنا الأرقام . بعد كل شيء ، يمكن أن يكون هناك الملايين والمليارات من الأرقام ...

كانت الرغبة في العثور بسرعة على مجموعة من العناصر المتتالية التي أصبحت الدافع لندوة الويب لدينا. علاوة على ذلك ، نحن لا نتحدث فقط عن المبلغ ، ولكن أيضًا عن المهام الأخرى ، على سبيل المثال ، حساب أي وظيفة ربط. وبالتالي ، نحن نتحدث عن العمليات التي لا يعتمد تنفيذها على ترتيب الحساب.

دعنا نعود إلى صفنا:



من الواضح ، إذا كنا نريد العثور على النتيجة بسرعة ، فنحن بحاجة إلى حساب بعض المبالغ مقدمًا. أول ما يتبادر إلى الذهن هو للطي في أزواج:



الآن ، إذا كنت بحاجة إلى العثور على مجموع الأرقام ، فيمكننا القيام بذلك على الفور تقريبًا. على سبيل المثال ، للعثور على مجموع المقطع المذكور أعلاه ، سيكون كافياً لإضافة 13 إلى 9. كل شيء أساسي: للعثور على مجموع أربعة أرقام ، قمنا بإضافة رقمين فقط .

نحن تعقيد المهمة:



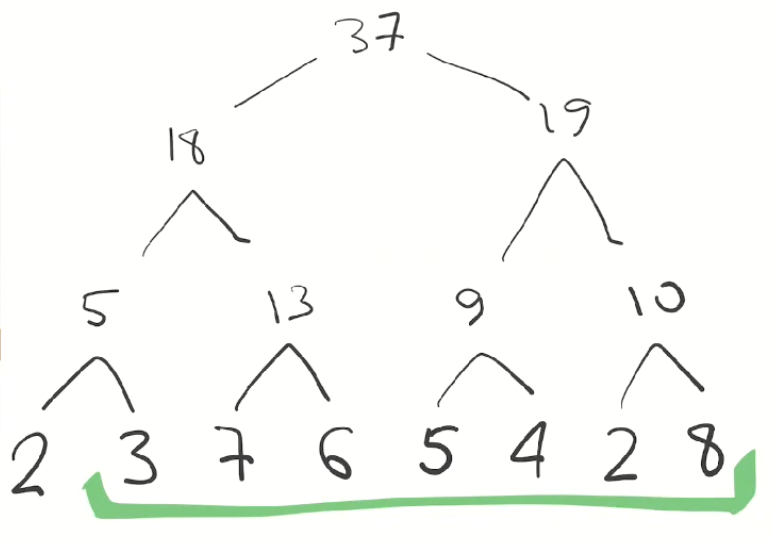
للعثور على مجموع هذا الجزء ، نحتاج إلى إضافة عناصر تغطي بطريقة أو بأخرى الجزء الخاص بنا:



بالطبع ، 3 + 13 + 19 = 35. لاحظ أنه للعثور على مجموع الأرقام السبعة ، أضفنا ثلاثة فقط . إذا كانت الشريحة مكونة من ألف عنصر ، فسيكون ذلك كافياً لإضافة 10 عناصر في المتوسط ​​، نظرًا لوجود تعقيد لوغاريتمي مع لوغاريتم أساسي 2. وسريع!

شجرة ثنائية كاملة

الشجرة الثنائية الكاملة هي شجرة ، ولكل عنصر منها طفلان بالضبط.

للعمل مع شجرة ثنائية كاملة ، يمكنك وينبغي عليك استخدام بنية بيانات مثل صفيف. ترقيم هذه المجموعة مناسب من واحد . نقوم بترقيم كل عنصر من عناصر الشجرة الثنائية بأرقام طبيعية من 1 إلى 2 ^ن -1:



إن الجمال الكامل لهذا النهج هو أنه من السهل جدًا حساب عدد الأطفال والآباء.
معادلة حساب "الطفل الأيسر": i * 2 ، "right": i * 2 + 1 .



على سبيل المثال ، نحسب أعداد الأطفال في العنصر الخامس:

1. 5 × 2 = 10 ؛
2. 5 × 2 + 1 = 11 .

وكيف من "الطفل" إلى الارتفاع إلى "الوالد"؟ نحن نستخدم عدد صحيح تقسيم i / 2

حسنا ، وكيفية تحديد ما إذا كان الطفل هو اليسار أو اليمين؟ الجواب هو ما يلي: الأطفال اليسار لديهم أرقام ، والأطفال الصحيح لديهم أرقام غريبة .

تذكر هذه النقاط.

بالعودة إلى مثالنا على شجرة ثنائية ، نسأل أنفسنا ، كيف يمكننا أن نبنيها؟ انظر ، لدينا أولاً مجموعة من الأرقام:



لذلك تحتاج إلى بناء شجرة ثنائية. ما مقدار الذاكرة اللازمة لتخزين الشجرة الثنائية ، والتي في أسفلها هذه العناصر؟

الإجابة على هذا السؤال هي 2n إذا كانت n قوة من اثنين.

نذهب أبعد من ذلك ، لأن سؤالين آخرين يطرحان أمامنا:

1. من أي عنصر تحتاج إلى وضع أرقام المصدر في صفيف شجرة ثنائية كاملة؟
2. من أي عنصر وفي أي اتجاه سنبدأ ملء الشجرة لدينا مع كميات محسوبة مسبقا؟

إجابة السؤال الأول بسيطة للغاية: لدينا 8 عناصر ، في المجموع سيكون هناك 16 عنصرًا في المصفوفة ، مما يعني أن العنصر الأول سيكون رقم 16 - 8 = 8. وسنبدأ في البناء من اليسار إلى اليمين ومن الأسفل إلى الأعلى ، بدءًا من العنصر 7 ، إضافة القيم في الأطفال ، مثل هذا:



بعد ذلك ، تحتاج إلى تحديد كيفية العثور على مجموع الجزء المطلوب. نعود إلى المثال الأول الخاص بنا ، ونعدد العناصر ونعرِّف مقطعًا ، ونشير إلى العنصر الأول في المقطع المراد إضافته بالحرف L ، والأخير بحرف R:



من الضروري الآن تقديم مفهوم آخر حتى تكون خوارزمية الإجراءات واضحة. نحن نتحدث عن مفهوم العناصر الأساسية وشرائحها الأساسية المقابلة. العنصر الأساسي هو أي عنصر من الصفيف بأكمله ، والجزء الأساسي يتوافق معه ، أي تلك العناصر من الصفيف الأولي الذي يمثل أولاده / أحفاده المباشرين. بالنسبة للعنصر الأساسي بالرقم 4 "5" ، سيكون الجزء الأساسي من 8 إلى 9 عناصر: ["2" ؛ "3"]:



بالنسبة للعنصر الأساسي الذي يحتوي على الرقم 10 - "7" (أطلقنا عليه اسم L) ، فإنه يتزامن مع الجزء الأساسي الخاص به. هل من الممكن توسيع هذا الجزء الأساسي دون تجاوز LR؟ في حالتنا ، يمكنك ذلك. قاعدة الحدود اليسرى هي: إذا كان الطفل يسارًا ، فيمكن توسيع الجزء الأساسي ، وسيكون العنصر الأساسي الجديد هو الأصل للجزء الحالي. بمعنى ، يمكننا كتابة ما يلي في البرنامج:



الآن دعنا ننتقل إلى العنصر الصحيح R. إنه عنصر أساسي وطفل يساري ، لذلك لم يعد بإمكاننا توسيع المنطقة (سنتجاوز هذا الجزء). لذلك ، يمكننا إضافة هذا العنصر إلى الإجابة:



بعد ذلك ، تحتاج العنصر الأيسر للانتقال إلى اليمين ، واليمين إلى اليسار. بالنسبة للعنصر الأيسر مع الفهرس L = 10 ، يكون الفهرس التالي هو 5 ، لأنه سينتقل إلى الأصل. لكنه سوف يذهب أولاً إلى اليمين ، ثم إلى أعلى:



لذلك ، انتقلت قيمة L إلى مستوى أعلى وقليلا إلى اليمين. كيف ستنخفض R؟ باستخدام الصيغة (R - 1) / 2.



هنا مثل هذه الخوارزمية. بالنسبة للقيم التالية للمتغيرات L و R ، عندها سيتم نقلها على النحو التالي:



إذا لم يكن هناك 8 عناصر في الشجرة ، ولكن هناك رقم غير مريح ، على سبيل المثال 12 ، فسوف يتعين علينا إضافة الشجرة (يجب أن تكون الشجرة الثنائية كاملة) إلى 16.
معادلة حساب عدد العناصر (يتم أخذ الجزء بأكمله من اللوغاريتم):



الآن نقوم بحساب الوظيفة النقابية لإيجاد الحد الأدنى . هنا شجرة لدينا وقطع:



كم مرة تعتقد أن العنصر 5 سيشارك في وظيفتنا - واحد أو اثنين؟ بالطبع ، واحد ، ولكن كيف يتم فحص هذا في الخوارزمية؟ في الواقع ، هذا العنصر هو إما الابن الأيمن أو الأيسر ، مما يعني أنه سيتم تنفيذ الإجراء إما L أو R.


+

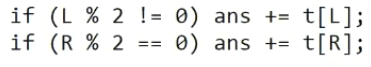
الآن النظر في عملية التغيير. دعنا نقول أن بعض العناصر قد تغير ، على سبيل المثال ، بدلاً من 7 ، 0 جاء. لكي تظل شجرة المقاطع الخاصة بنا في حالة صالحة للعمل ، نحتاج إلى تحديث جميع الآباء ، ونحن بحاجة إلى الانتقال إلى القمة.

حل مشكلة olympiad

أحد المتطلبات لمثل هذه المهام هو أن كل شيء يجب أن يعمل بسرعة. لذلك ، لدينا الشرط التالي:



سنحلها باستخدام المعرفة حول شجرة القطاعات. نتيجة لذلك ، حصلنا على رمز C # التالي:



نرسله للتحقق ، ونرى أنه تم اتخاذ القرار وإكماله ، مما يعني أن الخوارزمية تعمل.



هذا كل شيء ، إذا كنت تريد المزيد من التفاصيل ، شاهد الفيديو بأكمله . يمكنك أيضًا أن تقرأ في أوقات الفراغ مقالات المؤلف التالي لمدرستنا Evgeny Volosatov عن Habré :

- تحقيق التوازن بين الأشجار الحمراء السوداء - ثلاث حالات ؛
- الحصان يتحرك بت. لوح الشطرنج .