قوانين الفيزياء لا تتغير من وجهة نظر التغيير. ومع ذلك ، تساعد هذه الفكرة أجهزة الكمبيوتر على التعرف على ميزات معينة في المساحة المنحنية ذات الأبعاد الأعلى.
تعلم أجهزة الكمبيوتر قيادة السيارات ، وتغلب على أبطال العالم في ألعاب الطاولة ، وحتى كتابة النثر. بالنسبة للجزء الأكبر ، تعتمد ثورة الذكاء الاصطناعي على قدرات نوع واحد من الشبكات العصبية الاصطناعية ، وهو مستوحى من طبقات مترابطة من الخلايا العصبية في القشرة البصرية لعقل الثدييات. تبين أن ما يسمى "الشبكات العصبية التلافيفية" (SNA) مناسبة بشكل مدهش للعثور على أنماط في البيانات ثنائية الأبعاد - خاصة في مهام رؤية الكمبيوتر مثل التعرف على الكلمات المكتوبة بخط اليد أو الأشياء في الصور الرقمية.
ولكن عند تطبيقها على مجموعات البيانات التي لا يمكن اختزالها على شكل هندسي على متن الطائرة - على سبيل المثال ، على النماذج غير المنتظمة المستخدمة في الرسوم المتحركة ثلاثية الأبعاد للكمبيوتر ، لتوجيه السحب التي تولدها أجهزة الروبوت لتمييز العالم من حولهم - لم تعد هذه البنية الفعالة للتعلم الآلي (MO) يعمل بشكل جيد في عام 2016 ، ظهر نظام جديد هو التعلم العميق الهندسي (GGO) ، وكان الغرض منه هو إخراج نظام الحسابات القومية من الطائرة.
الآن ، حقق الباحثون هدفهم من خلال تطوير منصة نظرية جديدة لبناء NSs قادرة على العثور على أنماط على أي أسطح هندسية. تم تطوير هذه الشبكات العصبية التلافيفية المتوازنة في جامعة أمستردام ومختبر أبحاث كوالكوم AI بمشاركة باحثين مثل
تاكو كوهين وموريس ويلر وبيركاي كيتسانوغلو وماكس ويلينغ . يمكن لـ ESNS العثور على أنماط ليس فقط في المصفوفات ثنائية الأبعاد للبكسل ، ولكن أيضًا على الكرات والأجسام المنحنية بشكل غير متماثل. "هذه المنصة هي إجابة محددة للتحدي الذي تفرضه مشكلة التعلم العميق على الأسطح المنحنية" ، قال ويلينغ.
لقد تفوقت KESNS بالفعل بجد على سابقاتها في اكتشاف أنماط في محاكاة المناخ العالمي ، والتي تتم بشكل طبيعي على الكرة الأرضية. يمكن أن تكون الخوارزميات مفيدة أيضًا في تحسين رؤية الطائرات بدون طيار والروبوتات التي تتصور الأجسام ثلاثية الأبعاد ، ولاكتشاف الأنماط في البيانات التي يتم جمعها من الأسطح المنحنية ذات الأشكال غير المنتظمة للقلب أو المخ أو الأعضاء الأخرى.
تاكو كوهين ، أحد المهندسين المعماريين البارزين في CECNSإن حل مشكلة GO الذي وجده الباحثون خارج الطائرة له علاقة عميقة بالفيزياء. النظريات الفيزيائية التي تصف العالم ، مثل نظرية ألبرت أينشتاين العامة للنسبية أو النموذج القياسي في الفيزياء ، لها خاصية "قياس التماثل". هذا يعني أن حجم العالم وعلاقتهما لا يعتمدان على أنظمة مرجعية تعسفية (أو "معايرة") ؛ تظل كما هي دون تغيير بغض النظر عما إذا كان المراقب يتحرك أو يستريح ، أو المسافة بين الأرقام الموجودة على المسطرة. يجب تحويل القياسات المتخذة بوسائل مختلفة إلى بعضها البعض للحفاظ على الترابط بين الأشياء.
على سبيل المثال ، إذا قمنا بقياس طول ملعب لكرة القدم في الساحات ، وبعد ذلك بالأمتار ، فسوف نحصل على أرقام مختلفة ، لكن اختلافها سيكون متوقعًا. سيتلقى مصوران يلتقطان صورًا لكائن ما من نقطتين مختلفتين صورًا مختلفة ، لكن يمكن توصيلهما ببعضهما البعض. يضمن قياس التماثل اتساق النماذج المادية بغض النظر عن وجهة النظر أو وحدات القياس. تقبل KESNS نفس الافتراضات حول البيانات.
قال
كايل كرنمر ، عالم فيزياء في جامعة نيويورك يطبق MO على فيزياء الجسيمات: "لقد أرادوا إدخال فكرة الفيزياء في الشبكة العصبية - عندما لا توجد أي مناطق معينة". "لقد اكتشفوا كيفية القيام بذلك."
الهروب الطائرة
في عام 2015 ، صاغ
مايكل برونشتاين ، المتخصص في علوم الكمبيوتر في جامعة إمبريال كوليدج في لندن ، مصطلح "التعلم الهندسي العميق" لوصف المحاولات الأولى التي تم إجراؤها بعد ذلك لمغادرة الطائرة وتطوير NS قادرًا على البحث عن أنماط في البيانات ثلاثية الأبعاد. سرعان ما بدأ هذا المصطلح - والبحث -
جذرهعرف برونشتاين ورفاقه أن تجاوز الطائرة الإقليدية يتطلب إعادة اختراع أحد الإجراءات الحسابية الأساسية التي تجعل NSs فعالة للغاية في التعرف على الصور ثنائية الأبعاد. هذا الإجراء ، ما يسمى يسمح "Convolution" لطبقة NS بإجراء عملية رياضية على أقسام صغيرة من بيانات الإدخال ، ثم نقل النتيجة إلى طبقة الشبكة التالية.
"يمكنك أن تتخيل الحزمة كنافذة انزلاقية" ، أوضح برونشتاين. ينقل نظام الحسابات القومية الكثير من نوافذ التصفية هذه وفقًا للبيانات ، ويبحث كل منها عن نمط معين. في حالة صورة القط ، يمكن لنظام الحسابات القومية المدربين استخدام المرشحات التي تتعرف على علامات المستوى المنخفض بالبكسل ، مثل الوجوه. تنتقل هذه العلامات إلى الطبقات التالية من الشبكة ، وتجري تشابكات إضافية ، وتختار علامات المستوى الأعلى - مثل العيون أو الذيل أو الأذنين المثلثة. نتيجة لذلك ، تستخدم SNS المدربة على التعرف على القطط نتائج هذه التلاعب طبقة تلو الأخرى من أجل تحديد ما إذا كان هناك قطة في الصورة أم لا.
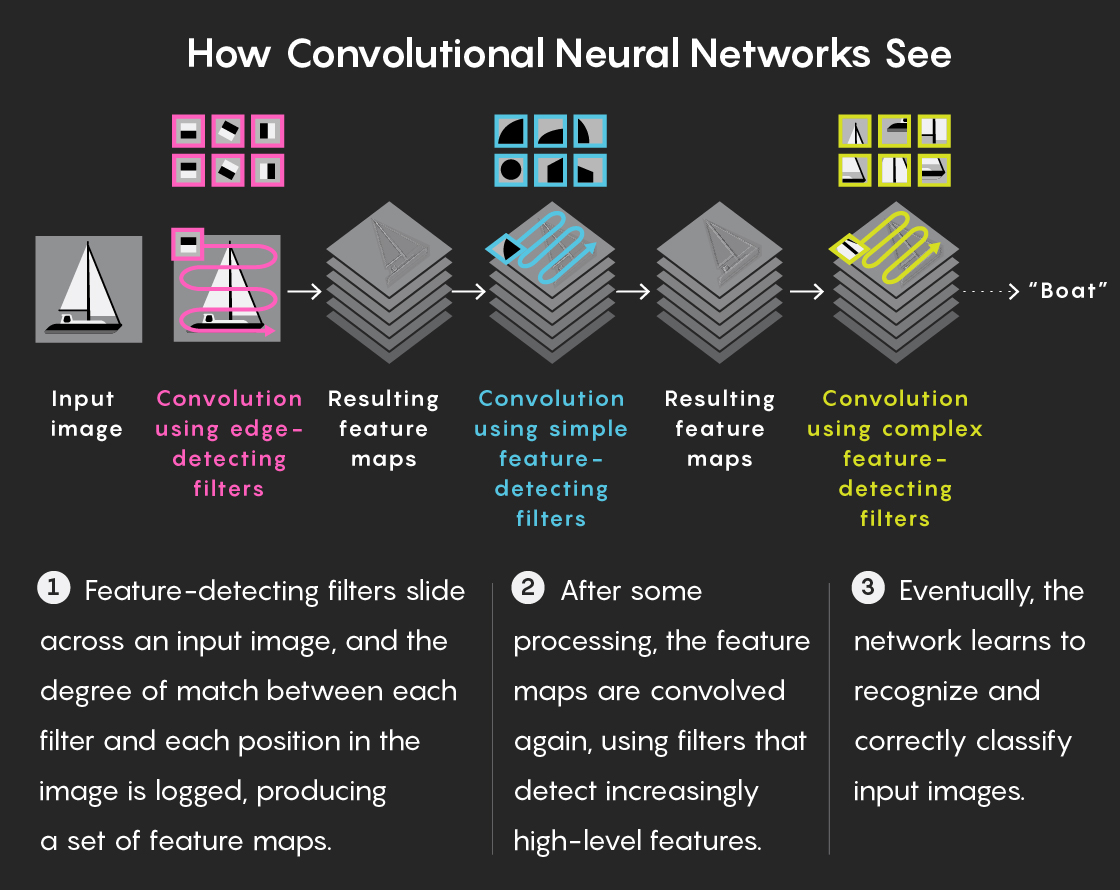كما ترى SNS:
- تنتقل الفلاتر التي تتعرف على العلامات على طول الصورة الواردة ، ويتم تسجيل درجة المصادفة مع كل مرشح في كل موضع ، مما يعطي خريطة للعلامات.
- بعد المعالجة ، يتم تحويل بطاقات الميزات مرة أخرى ، بالفعل باستخدام المرشحات التي تم تكوينها لميزات المستوى الأعلى.
- نتيجة لذلك ، تتعلم الشبكة التعرف على الصور وتصنيفها بشكل صحيح.
ومع ذلك ، فإن هذا النهج يعمل فقط على متن الطائرة. قال ويلنغ: "عندما تكون الطائرة التي تحتاج إلى تحليلها مشوهة ، فإنك تواجه مشكلات".
إن الالتفاف على سطح منحنٍ - في الهندسة ، يُطلق عليه اسم
مشعب طوبولوجي - يشبه دفع قطعة مربعة من ورق الرسم البياني إلى العالم ، في محاولة لنقل حدود محيط ساحل جرينلاند عليها بدقة. لا يمكنك ضغط الورق إلى جرينلاند دون سحقه ، مما يعني أن الرسم سيتم تشويهه عندما تقوم بتنعيمه مرة أخرى. يمكنك أن تميل الورقة على الكرة الأرضية في وقت ما ، وترسم الخطوط الكهربية ، وتنظر إليها من خلال الورقة (تُعرف هذه التقنية باسم
الإسقاط Mercator ) ، ولكن سيتم الحصول على تشوهات في هذه الحالة أيضًا. يمكنك إرفاق ورقة رسم بياني بخريطة العالم المسطحة ، وليس الكرة الأرضية ، ولكن بعد ذلك يمكنك فقط نسخ تشوهاتها - على سبيل المثال ، فكر في حقيقة أن الحافة العلوية بأكملها من الخريطة تعني بالفعل النقطة الوحيدة على الكرة الأرضية ، القطب الشمالي. وإذا تبين أن الصنف ليس مجالًا أنيقًا مثل الكرة الأرضية ، ولكنه شيء أكثر تعقيدًا وخطأًا ، مثل شكل ثلاثي الأبعاد للزجاجة ، أو بروتين مُرَكَّز ، فسيكون من الصعب عليه الإلتفاف عليه.
وجد برونشتاين وزملاؤه حلاً لمشكلة الالتواء على الفتحات غير الإقليدية في عام 2015. استبدلوا هيكل انزلاق النافذة بهيكل يشبه شبكة مستديرة أكثر من قطعة من ورق الرسم البياني - يمكن أن يميل ضد الكرة الأرضية (أو أي سطح منحني) دون التجاعيد ، دون تمزيق أو تمديد.
يؤثر تغيير خصائص عامل التصفية المنزلق بشكل إيجابي على فهم نظام الحسابات القومية لبعض العلاقات الهندسية. على سبيل المثال ، يمكن أن تفهم الشبكة تلقائيًا أن الرقم ثلاثي الأبعاد ، المنحني بطرق مختلفة - على سبيل المثال ، الشخص الذي يقف منتصباً ، والشخص الذي رفع ساق واحدة - هو كائن واحد ونفس الشيء ، وليس شخصين مختلفين تمامًا. أيضا ، هذا التغيير تحسن كبير في أداء الجمعية الوطنية. وقال برونشتاين إن SNS القياسية "استخدمت ملايين الأمثلة من الشخصيات ، وكانوا بحاجة إلى تدريب لأسابيع". "نحن نستخدم حوالي 100 شخصية في مختلف المواقف وتدريب الشبكة لمدة نصف ساعة تقريبًا."
في الوقت نفسه ، بدأ تاكو كوهين وزملاؤه من أمستردام في معالجة هذه المشكلة من الجانب الآخر. في عام 2015 ، لم يدرس كوهين ، الذي كان حينها طالب دراسات عليا ، مسألة الهروب من الطائرة. لقد كان مهتمًا بمشكلة هندسية عملية ، كما قال ، وهي: كفاءة البيانات ، أي مسألة كيفية تدريب NS باستخدام أمثلة أقل ، بدلاً من الآلاف أو الملايين المطلوبة عادة لهذا الغرض. "التعلم العميق بطيء جدا" ، قال كوهين. هذا لا يخلق أي مشاكل خاصة إذا قمت بتدريب SNS على التعرف على القطط (بالنظر إلى العرض الذي لا ينضب من صور القط على الإنترنت). ولكن إذا كنت تقوم بتدريس نظام الحسابات القومية على التعرف على شيء أكثر أهمية ، مثل الأورام السرطانية في صورة أنسجة الرئة ، فمن الصعب جدًا العثور على كمية كافية من بيانات التدريب - دقيقة طبياً ، وموسومة بشكل صحيح وخالية من حقوق الطبع والنشر. وعدد أقل من الأمثلة المطلوبة لتدريب الشبكة ، كان ذلك أفضل.
كان كوهين يعرف أن إحدى الطرق لزيادة فعالية البيانات هي إعطاء NS بعض الأفكار عن هذه البيانات مقدمًا ، على سبيل المثال ، أن سرطان الرئة لا يتوقف عن أن يكون ورمًا إذا كانت صورته مقلوبة أو معكوسة. تحتاج شبكة الالتفاف عادةً إلى تعلم مثل هذه المعلومات من نقطة الصفر ، ودراسة العديد من الأمثلة من نفس النمط ، المقدمة في أشكال مختلفة. في عام 2016 ، عمل كوهين وويلينغ معًا على
مقال يصف كيفية ترميز بعض هذه الافتراضات في NS في شكل تماثل هندسي. نجحت هذه الطريقة بشكل جيد لدرجة أنه في عام 2018 ، لخصها كوهين وماريكا وينكلز أكثر ،
مما أظهر نتائج واعدة في التعرف على سرطان الرئة في الصور المقطعية. كان NS لديهم القدرة على العثور على أدلة بصرية على وجود المرض باستخدام عشر فقط من البيانات التي تم تدريب الشبكات العصبية الأخرى.
واصل الباحثون من أمستردام تعميماتهم ، وفي النهاية توصلوا إلى قياس التباين.
توسيع التكافؤ
تشترك الفيزياء والتعلم الآلي في شيء مشترك. وفقا لكوهين ، "كلا المجالين مشغولان في مراقبة وبناء النماذج التي تتوقع نتائج الملاحظات اللاحقة." وقال إن المهم هو أن كلا المنطقتين يبنيان نماذج لأشياء غير منفصلة (من الصعب أن يكون هناك وصف واحد لذرة الهيدروجين ، والثاني لنفس الذرة ، مقلوب فقط) ، ولكن من فئات عامة. "والفيزياء ، بالطبع ، قطعت خطوات كبيرة في هذا."
equivariance
التوازي (أو "التباين" ، كما يفضل الفيزيائيون) هو الافتراض الذي اعتمد عليه الفيزيائيون في تعميم نماذجهم منذ آينشتاين. "هذا يعني فقط أنه إذا وصفت بشكل صحيح نوعًا من الفيزياء ، فيجب أن يكون هذا الوصف بغض النظر عن نوع" الحكام "الذين تستخدمهم ، أو بشكل عام ، أي نوع من المراقبين أنت" ، أوضح
ميراندا تشن ، عالم فيزياء نظري من جامعة أمستردام ، الذي كتب مع كوهين وغيره من العلماء
مقال عن دراسة العلاقة بين الفيزياء و KESNS. كما كتب آينشتاين نفسه في عام 1916: "يجب التعبير عن قوانين الطبيعة العامة من خلال المعادلات التي تعمل في جميع أنظمة الإحداثيات".
ميراندا تشن ، عالم فيزياء نظري من جامعة أمستردامأصبحت الشبكات العصبية التلافيفية واحدة من أنجح الطرق في الدفاع المدني بسبب استخدام مثال بسيط لمثل هذا المبدأ ، "نقل التوفيق". نافذة مرشح تتعرف على ميزة معينة في الصورة - على سبيل المثال ، الوجوه الرأسية - الشرائح (أو "اللف") على طول مجموعة من البيكسلات وتسجيل جميع الأماكن التي توجد فيها هذه الوجوه الرأسية ثم تنشئ "خريطة معالم" ، وتميز هذه الأماكن ، وتمررها إلى المستوى التالي للشبكة. يتم الحصول على إنشاء خرائط للميزات بسبب ملاءمة النقل: تفترض الشبكة العصبية أن نفس الميزة يمكن أن تظهر في أي مكان في المستوى ثنائي الأبعاد ، وأنها يمكن أن تتعرف على الوجه العمودي ، في الزاوية اليمنى العليا أو اليسرى السفلى.
وقال ويلر: "إن جوهر NS NS المتكافئ هو أخذ هذه التماثلات الواضحة ودمجها في بنية الشبكة بحيث تعمل هذه الخاصية كما لو كانت مجانًا".
بحلول عام 2018 ، وسع وايلر ، كوهين ، ومشرفهم ، ماكس ويلينغ ، هذا "العمل الحر" ليشمل أنواعًا أخرى من التكافؤ. يمكن لـ "الحسابات القومية المكافئة للمجموعة" التعرف على الميزات المدورة أو المنعكسة في الصور المسطحة دون الحاجة إلى التعلم من أشكال معينة من هذه الميزات ؛ يمكن لـ SNAs الكروية إنشاء خرائط للميزات بناءً على البيانات الموجودة على سطح الكرة دون تشويهها عند تحويلها إلى إسقاطات مسطحة.
هذا النهج لا يزال غير عالمي بما فيه الكفاية للعمل مع البيانات على بنية متكتلة غير منتظمة الشكل - أي على أي جسم في العالم الحقيقي تقريبًا ، من البطاطا إلى البروتينات ، من جسم الإنسان إلى انحناء الزمان والمكان. هذه المشعبات ليس لها تناسق "عالمي" حول التي يمكن أن تضع NS افتراضات متكافئة: أي من أقسامها يختلف عن جميع الأقسام الأخرى.
طي على الأسطح المنحنية التي لا تعمل الحسابات القومية القياسية. يمكن للمرشح ذي الكشف عن الحافة الذي ينزلق على طول هذا السطح ، اعتمادًا على المسار ، أن يتخذ اتجاهًا مختلفًا وينتج خرائط خرائط مختلفة.المشكلة هي أن تحريك مرشح مسطح فوق سطح يمكن أن يغير اتجاهه ، وهذا يتوقف على المسار المحدد. تخيل مرشح تم تهيئته للتعرف على نقش بسيط: بقعة مظلمة على اليسار ونقطة ساطعة على اليمين. حركه على سطح مستوٍ في جميع الاتجاهات الأربعة ، وسيكون دائمًا موجهاً بنفس الطريقة. لكن الوضع يتغير حتى على سطح الكرة. إذا كنت تحمل المرشح 180 درجة على طول خط الاستواء ، فسيظل اتجاهه - بقعة مظلمة على اليسار ، بقعة مضيئة على اليمين. ومع ذلك ، إذا قمت برسمه إلى نفس النقطة عبر القطب الشمالي للكرة ، فسيتم قلب الفلتر رأسًا على عقب. وقال انه لن يجد نفس النمط في البيانات ، لن تنتج نفس خريطة علامة. حرك المرشح على مجموعة أكثر تعقيدًا ، وفي النهاية سيكون قادرًا على الإشارة في أي اتجاه.
الهدف من ذلك ، أوضح ويلينغ ، هو أن ننسى تتبع التغييرات في اتجاه المرشح عند التحرك على مسارات مختلفة. بدلاً من ذلك ، يمكنك تحديد اتجاه واحد فقط (أو معايرة) للمرشح ، ثم تحديد طريقة متسقة لتحويل أي اتجاه آخر إليه.
تكمن المشكلة في أنه على الرغم من إمكانية استخدام أي معايرة في الاتجاه الأصلي ، إلا أن التحويل إلى خيارات أخرى يجب أن يحافظ على النمط الأصلي - تمامًا مثل تحويل سرعة الضوء من متر في الثانية إلى ميل في الساعة يجب الحفاظ على الكمية المادية الأساسية. يقول ويلينغ ، من خلال مقاربة توازي المقياس ، "تتغير الأرقام نفسها ، لكنها تتغير تمامًا بشكل متوقع".
Soen ، Weiler ، و Welling ترميز مقياس التماثل - "الغداء المجاني" - لنظام الحسابات القومية الخاص بهم في عام 2019. للقيام بذلك ، فرضوا قيودًا رياضية على ما يمكن لـ NS "رؤيته" في البيانات عند استخدام الإلتواء ؛ أنماط القياس المتكافئة فقط مرت عبر طبقات الشبكة. وقال فيلينج: "في الواقع ، يمكنك إعطائها أي سطح" - من الطائرات الإقليدية إلى الأجسام المنحنية بشكل تعسفي ، بما في ذلك الأنواع الغريبة مثل
زجاجة كلاين أو الزمان ثلاثي الأبعاد - "وستتغلب على GO على هذا السطح".
نظرية العمل
إن نظرية KESNS معممة لدرجة أنها تتضمن تلقائيًا افتراضات من المقاربات الهندسية السابقة لـ GO - على سبيل المثال ، التناوب الدوراني أو المرشحات المتحركة عبر المجالات. إنها تناسب الأسلوب السابق لـ Michael Bronstein ، والذي سمح لل NS بالتعرف على شخصية ثلاثية الأبعاد ، منحنية بطرق مختلفة. "مقياس التماثل هو منصة واسعة جدا. وقال برونستاين ، كحالة خاصة ، إنه يشمل ما فعلناه في عام 2015.
يعمل KESNS نظريًا على أي سطح منحني من أي بُعد ، لكن كوهين وزملاؤه شاركوا في فحصه على البيانات المناخية العالمية ، التي يكون هيكلها كرويًا. استخدموا نظامهم الأساسي لإنشاء نظام الحسابات القومية الذي يتعرف على أنماط الطقس المتطرفة ، مثل الأعاصير المدارية ، بناءً على بيانات محاكاة المناخ. في عام 2017 ،
استخدمت الحكومة والعلماء نظام الحسابات القومية المعياري لتحديد وجود الأعاصير في هذه البيانات بدقة 74 ٪ ؛ في العام الماضي ، تعرفت KESNS على
الأعاصير بدقة 97.9 ٪ (تخطت أيضًا نهجًا أقل تعميمًا لـ GO ، تم تطويره خصيصًا للكرات في 2018 - كانت نتيجة هذا النظام 94٪).
وقال مايور موديوندا ، عالم المناخ في مختبر لورنس بيركلي الوطني ، الذي يستخدم الدفاع المدني في عمله ، إنه سيواصل مراقبة تطور CESN. وقال: "هذا الجانب من الذكاء البشري ، وهو الاعتراف الصحيح للعلامات بصرف النظر عن اتجاهها في الفضاء ، هو ما نريد نقله إلى مجتمع المناخ".
تعتزم شركة Qualcomm للرقائق ، التي استأجرت مؤخرًا Cohen and Welling واشترت الشركة الناشئة التي أنشأتها ،
تطبيق نظرية KESNS على تطوير خوارزميات رؤية الكمبيوتر المحسّنة ، على سبيل المثال ، طائرة بدون طيار يمكنها رؤية كل 360 درجة في وقت واحد (مثل وجهة نظر مثل الأسماك العالمية يتم تعيين العين بشكل طبيعي على النطاق ، مثل بيانات المناخ العالمي).
وفي الوقت نفسه ، يكتسب KESNS شعبية بين علماء الفيزياء - على سبيل المثال ، يخطط Kranmer لجعلهم يعملون مع البيانات التي تحاكي تفاعل الجسيمات دون الذرية. « , , , », — . , , « ».
, , , , , . « YouTube, , , , , , », — . , - , . « , — , — ».
, , , , . « , , », — . , , , - . «» . « », — , , .
, , . « , - , — . – , : , ».